
P = NP, un problème à un million de dollars ?
Il n’y a qu’à, entend-on dire : avec les ordinateurs, on peut tout calculer ! Pour trouver le chemin de longueur minimale reliant un certain nombre de villes, il n’y a qu’à envisager tous les chemins et prendre le plus court. Pour déterminer si un nombre est premier, il suffit d’essayer de le diviser par tous les nombres plus petits que lui et voir si les restes sont nuls… Pour savoir si la position de celui qui commence aux échecs est gagnante, il n’y a qu’à examiner toutes les parties possibles. Hélas, ces calculs simples au premier abord sont beaucoup trop longs, même pour le plus puissant des ordinateurs. Peut-on les contourner ? C’est la question que pose l’énigme principale de l’informatique théorique « P = NP ? ».
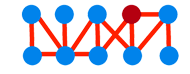
Savoir si un graphe (a) donné ayant n nœuds peut être colorié à l’aide de deux couleurs (bleue et rouge) sans que deux nœuds liés l’un à l’autre portent la même couleur est facile. On choisit un nœud qu’on colorie en bleu (b), on colorie tous ceux qui lui sont liés en rouge, et on poursuit ainsi de proche en proche en alternant les couleurs (c, d, e).
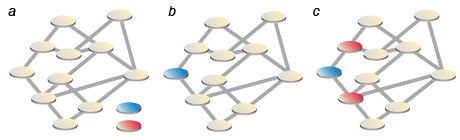
Si l’on rencontre une impossibilité, c’est qu’aucun coloriage bicolore n’est possible ; si on aboutit, c’est que la réponse est oui. Aucun retour en arrière n’est nécessaire dans l’utilisation de la méthode (les nœuds une fois colorés ne changent plus de couleur) et donc la méthode de coloriage prend un temps proportionnel au nombre n de nœuds. On dit que le problème de la 2-coloriabilité est polynomial.
Certains problèmes ne peuvent être résolus qu’en temps proportionnel à n2 (ou n3, n4, etc.), n mesurant la taille des données. On considère encore que ce sont des problèmes efficacement traitables et qu’ils constituent la classe P des problèmes qu’on peut résoudre en temps polynomial.
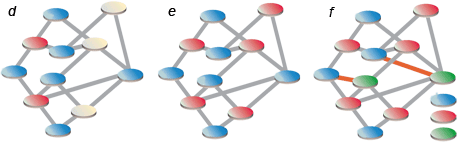
Le graphe (f) où il y a une liaison supplémentaire — il y a un triangle dont deux sommets ne peuvent être coloriés avec la même couleur — n’est pas 2-coloriable. Est-il coloriable avec trois couleurs ? Déterminer si un graphe donné ayant n nœuds peut être colorié à l’aide de 3 couleurs (bleu, rouge, vert) sans que deux nœuds reliés portent la même couleur est plus difficile qu’avec 2 couleurs. On ne connaît aucune méthode polynomiale du type de celle décrite au-dessus conduisant de manière certaine, soit à la réponse oui, soit à la réponse non. En revanche, vous pouvez colorier les nœuds selon une règle arbitraire, puis contrôler si c’est bon. Si vous avez de la chance, vous trouverez une solution dès le premier essai et ce sera fini. Sinon, vous recommencerez. Il y a, si vous n’avez pas la chance de trouver une solution, 3n tentatives à faire (il y a n nœuds pouvant chacun prendre trois couleurs différentes), et lorsque vous les aurez toutes essayées en utilisant un procédé d’énumération systématique, soit vous aurez trouvé une solution, et vous saurez que la réponse est « oui, le graphe est 3-coloriable », soit vous n’en aurez pas trouvé, et vous saurez que la réponse est « non, le graphe n’est pas 3-coloriable ».
Celui qui a toujours une chance parfaite (ou, ce qui revient au même, celui qui peut effectuer sur un ordinateur superpuissant tous les essais en parallèle, et d’un seul coup) conclut dès qu’il a fini un seul coloriage : soit il a réussi et le graphe est 3-coloriable, soit il a échoué et le graphe n’est pas 3-coloriable.
Le problème de la 3-coloriablité est un problème de la classe NP (non déterministe, polynomial) car, en ayant une chance parfaite, on le résout en temps polynomial. On ne sait pas si ce problème de la 3-coloriablité est dans la classe P, car les seuls algorithmes systématiques connus sont du type décrit au-dessus qui procèdent par énumération et demandent un temps de travail exponentiel (ici 3n essais).

Photo © Jeffrey Putman
La question « P = NP ? » est l’un de sept problèmes sélectionnés par l’Institut Clay en l’an 2000 : comme pour les six autres, une somme d’un million de dollars attend celle, celui ou ceux qui le résoudront. Certains affirment que c’est le plus important des sept problèmes et donc la principale énigme des mathématiques d’aujourd’hui. Il semble aussi être le seul dont la résolution aurait des conséquences pratiques (il est lié à des centaines d’énoncés concrets) et sa portée philosophique est la plus grande : la question « P = NP ? » concerne la nature de la recherche de solution(s) dans un ensemble exponentiel de possibilités, ce qui est le problème même de la recherche scientifique. La question « P = NP ? » signifie à peu près : « Ce que nous pouvons trouver rapidement lorsque nous avons de la chance, peut-il être trouvé aussi vite par un calcul intelligent ? ». Très sommairement, « l’intelligence peut-elle remplacer la chance ? »
Une autre formulation est : « Tout ce que l’on peut vérifier facilement, peut-il être découvert aisément ? ». Vérifier qu’un chemin dans un graphe passe par tous les nœuds du graphe sans jamais passer deux fois par le même nœud (chemin hamiltonien) est facile, trouver le chemin n’est pas facile (aujourd’hui, aucun algorithme efficace ne le permet). En revanche, si P = NP, savoir s’il existe des chemins hamiltoniens sera facile.
On entend souvent que le problème « P = NP ? » est, parmi les sept problèmes récompensés par l’Institut Clay, celui le plus susceptible d’être résolu par un amateur. C’est exact dans le sens où son énoncé est plus simple à comprendre que celui des autres problèmes et qu’il est envisageable qu’une solution élémentaire soit proposée demain par un génial passionné. La situation était la même pour le grand théorème de Fermat ; cela ne signifie cependant pas que la solution était facile et, pour Fermat, c’est un professionnel qui a résolu l’énigme. Nous avons aujourd’hui de fortes raisons de craindre que la question « P = NP ? » soit d’une profonde et extrême difficulté.
La résolution pourrait surgir d’un algorithme résolvant un problème NP-complet comme par exemple le problème du circuit hamiltonien :
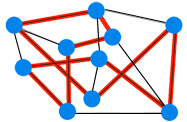
Soit un graphe G donné, existe-t-il une façon de suivre les arcs du graphe permettant de passer par tous les nœuds du graphe, sans passer deux fois par le même nœud et en revenant au point de départ ?
Les spécialistes considèrent improbable la résolution de l’un de ces problèmes NP-complets et pensent même que nous n’aurons pas la solution avant plusieurs dizaines d’années et par l’introduction d’idées radicalement nouvelles.
Certains problèmes de la classe NP concentrent en eux toute la difficulté de la classe NP, en ce sens que savoir les résoudre en temps polynomial permettrait de résoudre tout problème NP en temps polynomial, et prouver qu’il est impossible de les résoudre en temps polynomial prouverait définitivement que P ≠ NP. Le problème de la 3-coloriabilité est NP-complet (cela fut démontré en 1972 par R. Karp). En conséquence, si vous trouvez un algorithme qui le résout en temps polynomial, vous aurez prouvé que P = NP. Bien sûr l’examen des problèmes NP-complets est la voie la plus tentante pour résoudre l’énigme « P = NP ? ». Plusieurs milliers de problèmes NP-complets sont connus et on en découvre chaque année de nouveaux.
Voici quelques problèmes NP-complets.
- Problème du voyageur de commerce
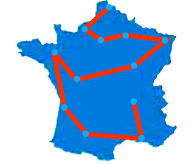
Un graphe G étant donné avec un nombre sur chaque arc indiquant sa longueur, et un nombre M étant fixé, existe-t-il un chemin du graphe ayant une longueur totale inférieure à M et passant par tous les nœuds du graphe ?
- Problème du sous-graphe planaire
 Un graphe G étant donné, ainsi qu’un entier k, peut-on trouver k nœuds du graphe G tels qu’en ne retenant que ces k nœuds et les arcs qui les relient, on ait un graphe planaire, c’est-à-dire représentable sur un plan sans que deux arcs ne se coupent ?
Un graphe G étant donné, ainsi qu’un entier k, peut-on trouver k nœuds du graphe G tels qu’en ne retenant que ces k nœuds et les arcs qui les relient, on ait un graphe planaire, c’est-à-dire représentable sur un plan sans que deux arcs ne se coupent ? - Problème des ensembles disjoints
 Une famille d’ensembles étant donnée, ainsi qu’un nombre k, existe-t-il k ensembles dans la famille qui soient disjoints deux à deux ? Exemple : { a, b, c }, { a, e, c, f, g }, { d, e, f }, { a, c, e, i }, { c, f, i }, { g, h, i }, { b, f, i }, { j, k, l, m }, { b, g, h, i } avec k = 4. Réponse. OUI : { a, b, c }, { d, e, f }, { g, h, i }, { j, k, l, m }
Une famille d’ensembles étant donnée, ainsi qu’un nombre k, existe-t-il k ensembles dans la famille qui soient disjoints deux à deux ? Exemple : { a, b, c }, { a, e, c, f, g }, { d, e, f }, { a, c, e, i }, { c, f, i }, { g, h, i }, { b, f, i }, { j, k, l, m }, { b, g, h, i } avec k = 4. Réponse. OUI : { a, b, c }, { d, e, f }, { g, h, i }, { j, k, l, m } - Problème de la séparation équitable Une suite de nombres entiers étant donnée, peut-on la séparer en deux paquets ayant la même somme ? Exemple 1, 2, 2, 2, 3, 4, 4 Réponse OUI, car 2 + 2 + 2 + 3 = 1 + 4 + 4
- Les équations quadratiques Trois nombres entiers a, b, c, étant donnés, existe-t-il des entiers x et y tels que ax2 + b y = c ?
- Problème des Sudokus généralisés
 Étant donnée une grille de Sudoku généralisé (c’est-à-dire ayant n2 lignes, autant de colonnes et autant de sous-carrés au lieu de 9), cette grille possède-t-elle une solution ?
Étant donnée une grille de Sudoku généralisé (c’est-à-dire ayant n2 lignes, autant de colonnes et autant de sous-carrés au lieu de 9), cette grille possède-t-elle une solution ?
Gödel interroge von Neumann

Kurt Gödel, mathématicien autrichien.
Kurt Gödel, dans une lettre (retrouvée récemment) qu’il envoya à John von Neumann en 1956 quelques mois avant que celui-ci ne meure, est le premier à avoir formulé clairement la question en insistant sur son importance concrète en mathématiques. Il y explique que si P = NP (sans employer cette notation, introduite en 1972), bien des questions mathématiques deviendront faciles par le procédé détaillé dans ce qui suit. Pour résoudre une question ouverte Q, on recherchera parmi toutes les démonstrations de longueur n (n entier fixé), dans un système donné d’écriture des démonstrations (par exemple dans celui de la théorie des ensembles) s’il y en a une amenant la réponse. S’il y en a une, on la trouvera vite, car nous sommes dans l’hypothèse où il y a un algorithme rapide, et on aura résolu le problème Q ; si l’on n’en trouve pas et que le n essayé est assez grand, alors « il n’y aura plus de raison sérieuse de rester préoccupé par le problème » écrit Gödel.
L’indécidabilité algorithmique des systèmes logiques – c’est-à-dire l’affirmation qu’il n’existe pas d’algorithmes indiquant en un temps fini pour toute formule F si elle est démontrable ou non dans un système fixé – est un résultat négatif central en logique qui fut établi dans la décennie 1930 par Alonzo Church et Alan Turing. Il s’agit là cependant de montrer que la formule F est démontrable en un temps fini, mais pas nécessairement petit. Gödel estime que sa version « concrète », « utilisable », est justement l’affirmation P ≠ NP. L’enjeu est capital : c’est la version en termes finis du problème de l’indécidabilité.
La preuve que P = NP serait une surprise et les chercheurs pensent que P ≠ NP. En apparence très simple, la question résiste. Les recherches menées depuis 40 ans ne sont cependant pas restées vaines, car à défaut de suggérer ce qu’il faut faire, elles donnent une meilleure compréhension des raisons des échecs et de l’inutilité de l’exploration de certaines voies.
Une enquête menée en 2002 par William Gasarch auprès de 100 mathématiciens et informaticiens théoriciens au sujet de la conjecture « P = NP ? » mesure l’état d’esprit des personnes les plus compétentes sur cette question.
Concernant la résolution prochaine de la conjecture, les avis sont relativement optimistes : 45 pensent que la conjecture sera résolue avant 2050 ; 27 qu’elle le sera après 2050 et 5 qu’elle ne sera jamais résolue. Les autres ne se prononcent pas.
Parmi les 100 personnes : 61 croient que P ≠ NP, 9 penchent plutôt vers P = NP. Les autres ne se prononcent pas ou craignent que la question soit indécidable.
John Conway, qui est convaincu que P ≠ NP, précise que le problème pourrait bien ne pas être vraiment difficile, et que c’est juste parce que nous nous intéressons à cette question depuis trop peu de temps et que nous n’avons pas encore développé les outils adaptés à sa résolution. Dans le futur, il se pourrait bien, d’après lui, que le résultat (une fois démontré) soit juste mentionné en note de bas de page !
Yuri Gurevich, qui pense que P = NP, considère que même lorsque nous aurons trouvé un algorithme polynomial pour un problème NP-complet, cela n’aura pas d’importance concrète. Cette idée plusieurs fois exprimée est fondée sur le fait qu’un problème dont les algorithmes mettent un temps de calcul polynomial avec un polynôme de degré élevé n’est pas vraiment résolu efficacement.
Juris Hartmanis qui soutient que P ≠ NP pense que la démonstration viendra assez rapidement et précise qu’il ne serait pas surpris qu’elle soit assez courte. Donald Knuth envisage l’idée que P = NP, mais qu’on n’en trouverait qu’une preuve non constructive ne donnant pas en pratique d’algorithme polynomial pour les problèmes NP-complets.
Ming Li espère que le problème restera ouvert encore 100 ans, car la NSF (National Science Foundation) doit croire que l’informatique théorique est importante et qu’il faut la financer.
Michael Sipser avait parié avec Len Adleman une once d’or que le problème serait résolu avant la fin du XXe siècle – il a donc dû payer son pari perdu –, il reste optimiste, mais se refuse à faire une nouvelle prédiction et surtout un autre pari.
Avi Wigderson de l’Institute for Advanced Study de Princeton pense que nous ne sommes pas assez avancés pour faire un pronostic. « La seule chose que je puisse dire de manière certaine est qu’il s’agit d’une des plus importantes et intéressantes questions que l’humanité s’est jamais posée, et que plus de gens et plus de moyens devraient y être consacrés. »
Notre but ici sera d’indiquer quelques résultats concernant « P = NP ? », et la façon dont on doit les interpréter. Nous nous demanderons en particulier si, comme le suggèrent certains mathématiciens, il est souhaitable d’ajouter l’axiome P ≠ NP à ceux admis habituellement.
La prise de conscience de l’importance du problème est venue de la découverte du résultat suivant, démontré par Stephen Cook et Leonid Levin au début des années 1970. Certains problèmes dénommés NP-complets concentrent en eux toute la difficulté des problèmes NP (problèmes qu’on peut résoudre en temps polynomial lorsque l’on a de la chance).
Autrement dit, si vous réussissez à maîtriser un seul problème NP-complet, alors vous maîtriserez tous les problèmes NP. Le plus étonnant est que les problèmes NP-complets sont nombreux et qu’en quelques années, des centaines d’entre eux ont été identifiés dans des sujets en apparence sans rapport : théorie des graphes, jeux, arithmétique, programmation, théorie des langages, optimisation, algèbre, etc. Si vous réussissez à trouver un algorithme rapide (accompli en un temps polynomial) pour l’un d’eux (celui qui vous semble le plus facile !), vous aurez du même coup trouvé un algorithme rapide pour tous les autres… et prouvé que P = NP. Inversement, si vous démontrez qu’un seul problème NP-complet ne peut être résolu efficacement, alors vous aurez démontré qu’aucun problème NP-complet ne peut l’être… et donc que P ≠ NP.
Le problème des mots croisés est un exemple de problème NP-complet. Une liste L finie de mots étant donnée, ainsi qu’une grille de mots croisés de taille n x n (une grille vide avec quelques cases noircies), peut-on remplir la grille de mots croisés, avec les règles habituelles, en utilisant des mots parmi ceux de L ? Ce problème est NP, car avec de la chance, en plaçant les mots au hasard, vous composez la grille cherchée. Il est NP-complet ainsi que l’ont montré H. Lewis et C. Papadimitriou et donc celui qui trouve un algorithme rapide pour résoudre les grilles de mots croisés prouve que P = NP ; celui qui réussit à démontrer qu’il n’existe pas d’algorithmes rapides pour les grilles de mots croisés prouve que P ≠ NP. Il ne vous reste plus qu’une chose à faire : essayer !
Dans la période qui a suivi la découverte de S. Cook et L. Levin, des dizaines de solutions ont été proposées, conduisant à une réponse ou à son opposé, mais toutes contenaient (au moins) une erreur : soit l’algorithme proposé n’était pas efficace pour certains jeux de données, soit la démonstration qu’aucun algorithme ne pouvait résoudre rapidement le problème était erronée en un point.
Oded Goldreich, spécialiste de ces questions, en est arrivé à expliquer sur sa page Web personnelle qu’il ne chercherait plus à vérifier ou à critiquer les solutions concernant la question fondamentale de l’informatique théorique. Cela, sauf si l’auteur de la solution explique en termes clairs en quoi sa méthode est nouvelle et pourquoi elle évite les écueils sur lesquels les milliers de tentatives précédentes ont échoué. Bien d’autres chercheurs ont adopté la même attitude à propos de la conjecture « P = NP ? », attitude comparable à celle de l’Académie des sciences de Paris qui décréta en 1775 qu’elle cesserait d’examiner les mémoires qu’on lui ferait parvenir concernant (a) la quadrature du cercle ; (b) la trisection de l’angle ; (c) la duplication du cube et (d) le mouvement perpétuel. À l’époque, aucun de ces problèmes n’avait pourtant été résolu ; les trois premiers furent prouvés impossibles au XIXe siècle.
Un résultat démontré en 1975 par T. Baker, J. Gill et R. Solovay peut justifier l’attitude de Goldreich sur la conjecture « P = NP ? » et signifie que les idées trop simples pour aborder la conjecture n’aboutiront pas.

Pour étudier le problème « P = NP ? », on considère des univers fictifs où certains calculs ne coûtent rien car des oracles répondent instantanément quand on les interroge. On peut par exemple envisager qu’un oracle indique, pour tout nombre entier n, si n est un nombre premier ou non. Cette notion d’oracle permet de définir la classe de complexité Poracle des problèmes qu’on peut résoudre en temps polynomial (soit immédiatement, soit en temps polynomial grâce aux facultés de l’oracle) et la classe NPoracle des problèmes pour lesquels une chance parfaite et les services de l’oracle permettent de les résoudre en temps polynomial. Pour certains oracles, on démontre que :
Poracle = NPoracle
et, pour d’autres, on prouve que :
Poracle ≠ NPoracle.
Ces résultats indiquent qu’afin de résoudre la conjecture « P = NP ? », il faudra trouver des démonstrations impossibles à adapter dans ces univers avec oracles, car sinon on se retrouverait devant une contradiction, et donc que ces démonstrations seront nécessairement assez compliquées. J. Hartmanis et J. E. Hopcroft ont aussi prouvé que si on se fixe un oracle au hasard, alors presque certainement :
Poracle ≠ NPoracle.
Ce dernier résultat a été vu comme un indice en faveur de P ≠ NP. T. Baker, J. Gill et R. Solovay ont montré en 1975 que pour certains oracles la théorie des ensembles ne permet de démontrer ni Poracle = NPoracle ni Poracle ≠ NPoracle.
Autrement dit, dans certains cas, la formule Poracle = NPoracle est indécidable dans la théorie usuelle des ensembles. Ce résultat est considéré comme un indice en faveur de l’idée que P = NP est indécidable dans la théorie des ensembles. Malheureusement on ne sait pas transformer ces indices en preuves.
Indécidables ?
Sachant qu’une fois choisi un système pour écrire les démonstrations, un résultat vrai peut y être indémontrable (c’est le phénomène de l’indécidabilité découvert par Gödel en 1931), il est tentant, à chaque fois qu’on ne réussit pas à démontrer quelque chose, d’émettre l’hypothèse que ce doit être indécidable (sous-entendu : vis-à-vis du système le plus couramment utilisé en mathématiques qui est la théorie des ensembles).
La question est sérieuse, car on sait par exemple que l’hypothèse du continu (notée HC, elle affirme qu’il n’y a pas d’infini de taille intermédiaire entre celui des entiers et celui des nombres réels) sur laquelle les mathématiciens de la fin du XIXe et du début du XXe siècle s’épuisaient, est indécidable dans la théorie des ensembles. Si celle-ci est non contradictoire, on peut au choix ajouter que HC est vraie ou fausse sans introduire de contradiction. De même, la démonstration de l’axiome des parallèles est impossible à partir des autres axiomes de la géométrie du plan (c’est donc un indécidable de la géométrie du plan). Ne serions-nous pas dans une situation analogue à propos de la question « P = NP ? ».
Le résultat de J. Hartmanis et J. E. Hopcroft (concernant l’indécidabilité de certaines variantes de la conjecture) est partiel et insatisfaisant : il répond à une question proche, mais différente de celle qui nous intéresse. C’est pourquoi, depuis, de nombreux chercheurs ont tenté d’aller plus loin. Les méthodes utilisées pour démontrer l’indécidabilité de l’hypothèse du continu ne marchent pas pour P = NP (on a bien sûr tenté de les adapter), il a donc fallu réduire ses ambitions en considérant des systèmes logiques plus faibles que la théorie des ensembles (l’indécidabilité vis-à-vis d’un système faible est plus facile à démontrer). Plusieurs pas dans cette voie ont progressivement été faits.
En 1979, R. DeMillo et R. Lipton ont établi que dans une théorie appelée ET suffisamment forte pour permettre la démonstration d’une bonne partie des résultats d’arithmétique (par exemple qu’il existe une infinité de nombres premiers) ni P = NP ni P ≠ NP, ne pouvaient être démontrés. Dans ET, la conjecture à un million de dollars est donc indécidable. Le système ET est malheureusement assez artificiel et trop faible pour qu’on puisse se contenter de ce résultat. Celui-ci confirme cependant que pour faire la démonstration de P = NP ou de P ≠ NP, il faut employer des méthodes assez complexes, non exprimables dans ET.
L’idée que la conjecture « P = NP » pourrait être indécidable fut renforcée en 1993 par un résultat de A. Razborov et S. Rudich. D’après leurs démonstrations, si l’on arrivait à prouver que P ≠ NP par les techniques que l’on avait l’habitude d’essayer, alors cela entrerait en contradiction avec certaines conjectures jugées très probables concernant les générateurs pseudo-aléatoires (des algorithmes permettant de simuler le hasard).
Impuissances naturelles
En clair, ou bien les conjectures classiques sur les générateurs pseudo-aléatoires sont fausses et cela serait très étonnant ; ou bien P = NP, ce qui serait au moins aussi étonnant ; ou bien, pour démontrer l’affirmation P ≠ NP, il faut découvrir des techniques différentes de celles qu’on croyait les plus naturelles.
De leur résultat, on déduit aussi que, sauf si certaines conjectures jugées très vraisemblables sont fausses, alors P ≠ NP est indécidable dans des systèmes logiques relativement puissants (plus intéressants que ET, mais moins puissants que la théorie des ensembles). D’autres travaux exploitant des résultats du logicien G. Kreisel sont venus refroidir l’espoir que nous nous approchions d’une démonstration de l’indécidabilité de la question « P = NP ? » dans un système fort. En effet, l’analyse logique de la formule P ≠ NP montre que les techniques connues pour démontrer l’indécidabilité ne s’appliquent pas à la formule P ≠ NP.
En résumé, la situation semble bien pire que ce que l’on aurait pu imaginer : les méthodes les plus simples et les plus naturelles pour montrer que P = NP, ou P ≠ NP, ne peuvent pas marcher, c’est certain ; mais les méthodes habituellement utilisées en logique pour montrer qu’une formule est indécidable relativement aux systèmes logiques forts sont incapables d’aboutir à un tel résultat pour la formule P ≠ NP.

Photo © Remco Douma
Même si c’est plus facile à dire qu’à faire, la conclusion est que l’introduction d’idées nouvelles est donc indispensable à propos du problème de la lettre à von Neumann, et cela que notre but soit une résolution directe du problème ou la démonstration de son indécidabilité. Ces résultats inquiétants, qui suggèrent que la conjecture « P = NP ? » pourrait être la plus difficile de tous les temps, sont d’une réelle utilité pour avancer vers la résolution du problème : on ne sait pas comment il faut s’y prendre, mais on sait que des classes importantes de méthodes ne peuvent pas aboutir et qu’il ne faut donc pas perdre son temps à les essayer.
L’analyse logique des démonstrations et des preuves guide les mathématiciens et agit comme un ange qui soufflerait aux chercheurs : « Non, par là tu ne peux rien trouver, essaye d’ouvrir une nouvelle porte. » Jamais à ma connaissance, la logique mathématique n’avait aussi bien montré sa puissance et sa capacité à guider une recherche par des analyses abstraites de méta niveau : la logique joue ici pleinement son rôle de « théorie de la théorie », et cette capacité est une véritable aubaine pour le mathématicien qui, en même temps qu’il explore l’espace des démonstrations dans lequel il en cherche une particulière, fait la théorie de cet espace de démonstrations et en tire des indications cruciales.
Lorsqu’on ne peut démontrer un résultat, ni son opposé, une idée vient : ne pourrait-on choisir de l’ajouter aux axiomes de la théorie qu’on utilise (par exemple, la théorie des ensembles) ? C’est ainsi que Gregory Chaitin a récemment proposé d’adopter deux nouveaux axiomes : l’hypothèse de Riemann — notée RH, elle concerne la répartition des nombres premiers — et l’affirmation P ≠ NP. L’idée est intéressante, mais elle ne fait pas l’unanimité auprès des chercheurs. Lorsqu’un résultat comme l’hypothèse du continu HC est démontré indécidable, on peut juger intéressant de l’ajouter (lui ou sa négation) comme nouvel axiome, car on est certain de ne pas introduire de contradictions dans la théorie que l’on complète. Concernant HC, la situation a d’ailleurs récemment évolué et une série de résultats du logicien Hugh Woodin suggère fortement qu’on doit considérer que HC est fausse et qu’il y a des ensembles de nombres dont la taille est intermédiaire entre celle des entiers et celle des réels. Cependant, la conclusion concernant HC et sur laquelle on obtiendra peut-être un accord des spécialistes n’est pas qu’il faut ajouter non-HC, mais qu’il faut ajouter un certain axiome (découvert par H. Woodin) dont les conséquences sont riches et séduisantes, et qui, entre autres choses, permet de déduire que HC est fausse.
Un nouvel axiome ?
Habituellement, choisir les axiomes d’une théorie se fait à partir de leur évidence intuitive immédiate. On dit qu’ils sont vrais a priori : pour le domaine d’objets considérés – les entiers, les ensembles, etc. – qu’on tente d’axiomatiser, il est naturel et évident que A, B, C, etc. et donc l’on adopte les axiomes A, B, C, etc. Dans les cas qui nous intéressent (HC, RH, P ≠ NP), l’ajout d’axiomes ne peut se faire que par des arguments a posteriori : un bon axiome est un énoncé dont les conséquences se révèlent riches, cohérentes et raisonnables. Dès 1947, Gödel lui-même envisageait cette nouvelle méthode pour ajouter des axiomes : « Il se pourrait que certains axiomes possèdent des conséquences si nombreuses, produisant un tel éclaircissement dans un domaine et conduisant à des méthodes si puissantes pour résoudre les problèmes (autant que possible d’une manière constructive) que, indépendamment de toute nécessité intrinsèque, ils devraient être adoptés, comme on adopte les théories physiques ».
Pour non-HC, il semble qu’on y soit presque : on ne le rajouterait pas lui-même, mais on ajouterait l’énoncé plus puissant trouvé par H. Woodin dont l’analyse a posteriori a été satisfaisante. Pour l’hypothèse de Riemann et pour P ≠ NP en revanche, on n’y est pas du tout, et il ne semble pas que l’idée de Gregory Chaitin de les prendre comme axiomes puisse recueillir un large soutien. À cela deux raisons au moins.
D’abord, il n’a pas été démontré qu’il s’agissait d’indécidables relativement à la théorie des ensembles ou relativement à des théories suffisamment fortes. On ne doit donc pas renoncer à les démontrer. Il serait absurde et ridicule d’ajouter un énoncé et de découvrir quelques années après que lui-même ou (pire !) sa négation se démontre !
En effet, l’exemple de la conjecture de Borsuk (qui concerne une caractérisation de la dimension des espaces géométriques) nous rend méfiant. Formulée en 1933, cette conjecture séduisit tous les spécialistes qui étaient convaincus de sa justesse. Or, après 60 ans de recherches infructueuses, J. Kahn et G. Kalai découvrirent un contre-exemple (de dimension 2 014 !) qui montrait de manière indubitable que la conjecture de Borsuk était fausse. L’intuition, même des meilleurs spécialistes, et même lorsqu’ils sont unanimes, ne donne aucune garantie.
Une deuxième raison pour ne pas ajouter comme axiome l’hypothèse de Riemann RH ou P ≠ NP est que les adopter comme axiomes n’apporterait pas grand-chose. À l’inverse, la démonstration d’une des deux hypothèses serait d’un très grand intérêt et ouvrirait sans doute des pistes à la démonstration d’une multitude d’autres énoncés. Les prendre comme axiomes (ce qui revient plus ou moins à baisser les bras) aurait plus de conséquences négatives que positives.
Même si, en l’état actuel de nos connaissances, ni RH ni P ≠ NP ne semblent devoir être adoptés comme axiomes, notons que les deux cas doivent être distingués. L’analyse logique de RH montre que si l’on réussissait à prouver qu’elle est indécidable dans un système fort, on aurait automatiquement démontré qu’elle est vraie. Certains énoncés mathématiques ne peuvent être démontrés indécidables vis-à-vis des systèmes intéressants (arithmétique de Peano et théorie des ensembles) que s’ils sont vrais. En effet, dans ces systèmes, tous les énoncés d’arithmétique élémentaire du type « 2 6 = 8 » ou « 13 est premier » sont prouvables.
Prenons, pour le montrer, le cas simple de la conjecture de Goldbach : Tout nombre pair à partir de 4 est somme de deux nombres premiers. Si elle est fausse, c’est qu’il y a un nombre pair dont aucune décomposition sous forme de sommes de deux nombres ne comporte deux nombres premiers. Si un tel nombre existe, alors ce résultat d’arithmétique élémentaire est toujours découvert par un système intéressant. Donc si une théorie montre que Goldbach est indécidable, alors elle montre qu’on ne peut trouver aucun nombre pair qui ne soit pas somme de deux nombres premiers, et donc elle démontre Goldbach.
On peut avancer le même raisonnement sur la conjecture de Riemann RH : si on démontrait qu’elle est indécidable vis-à-vis d’un système intéressant, on aurait démontré qu’elle est vraie (autrement dit, il n’y a pas d’espoir, même à long terme, qu’on se retrouve dans la situation de HC). Pour P ≠ NP, rien de tel, et même si aujourd’hui on a repéré une série d’obstacles sur le chemin d’une preuve que cet énoncé est indécidable relativement à un système fort, on pourra peut-être y arriver, auquel cas se posera alors vraiment la question de l’adopter comme nouvel axiome. Autrement dit : il est encore moins justifié d’adopter P ≠ NP comme axiome que RH.
Les mathématiques découvrent sans cesse des obstacles inattendus dont on a l’impression qu’ils sont de difficulté croissante. La logique mathématique, par les outils puissants qu’elle a mis au point, permet de pénétrer au plus profond des raisons de ces obstructions. Dans certains cas exceptionnels (comme pour non-HC), elle fournit des arguments justifiant qu’on ajoute de nouveaux axiomes à nos théories préférées, dont Gödel en 1931 nous a démontré qu’elles resteraient irrémédiablement incomplètes (même après ces ajouts). Pour la conjecture « P = NP ? », qui est peut-être la plus importante des énigmes mathématiques contemporaines, nous n’en sommes pas là, et nous n’avons donc pas d’autre choix que de poursuivre l’exploration.
Quelques références vous sont proposées pour en savoir plus sur le problème « P = NP ? » et sur les différentes conjectures évoquées dans cet article.
En français
- Patrick Dehornoy, Progrès récents sur l’Hypothèse du continu, Séminaire Bourbaki, 55e année, n° 915, 2002-2003
En anglais
- Andreï Raïgorodskii, The Borsuk Partition Problem : The Seventieth Anniversary, in The Mathematical Intelligencer, 26-3, pp. 4-12, 2004
- Gregory Chaitin, Thoughts on the Riemann Hypothesis, in The Mathematical Intelligencer, 26-1, pp. 4-7, 2004
- Scott Aaronson, Is P Versus NP Formally Independant ?, in Bulletin of the EATCS, n° 8, pp. 109-136, 2003
- William Gasarch, The P = NP ? Poll, in SIGACT News 36, 33(2), 2002
- Michael Sipser, The History and Status of the P versus NP question, in Proceedings of the ACM STOC’ 92, pp. 603-618, 1992
Une première version de ce document est parue dans la rubrique « Logique et calcul » de la revue Pour la Science, n°334, en août 2005.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Jean-Paul Delahaye
Professeur émérite d'informatique à l'Université des Sciences et Technologies de Lille (Lille 1) et chercheur au Centre de recherche en informatique, signal et automatique de Lille (CRIStAL).