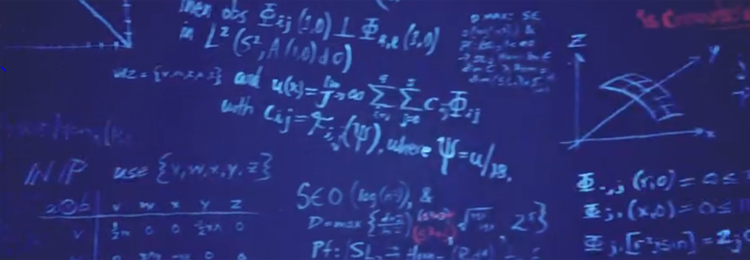
P=NP : élémentaire, ma chère Watson ?
Pour L’informatique – ou presque – dans les films, nous avons visionné cet épisode.

Elementary (CBS)
Il est vrai qu’un million de dollars sont à gagner pour résoudre cette énigme. C’est un des sept prix de l’Institut Clay. On peut donc imaginer, comme dans cet épisode, que ce prix attise des convoitises, même celles de mathématiciens peu scrupuleux. Il ne fait également aucun doute que si elle était trouvée, la solution de la conjecture P=?NP intéresserait la NSA. Et cela même si aucune application ne peut en être tirée immédiatement. En effet, il est bon d’avoir une longueur d’avance, même théorique, sur ses concurrents.
L’énigme P=?NP est une question ouverte de la théorie des classes de complexité. Un problème est dans la classe de complexité P s’il existe un algorithme pour le résoudre en temps polynomial. Un problème est dans la classe NP s’il existe un algorithme pour vérifier en un temps polynomial qu’on a trouvé une solution. Tout problème dans la classe P est dans la classe NP, mais la réciproque est une question ouverte. Les problèmes du voyageur de commerce, du sac à dos sont des problèmes de la classe NP, ils sont même NP-complets : si on sait les résoudre en temps polynomial, alors on sait le faire pour tout problème de la classe NP et on a démontré que P=NP.
Si on parvient à démontrer que P est différent de NP, on aura démontré que certains types d’algorithmes n’existent pas. La grande majorité des spécialistes qui travaillent à ce problème pensent que c’est la bonne réponse.
L’épisode de la série envisage le scénario inverse : P=NP est enfin démontré !
Si on parvient à démontrer que P=NP en construisant un algorithme polynomial pour un problème NP-complet, alors on saura résoudre rapidement tout problème NP. Cependant, rapidement signifie ici en temps polynomial. Si on résout un problème en temps n10, c’est quand même très lent et éventuellement sans intérêt. Si quelqu’un propose un jour une preuve correcte que P=NP, il faudra voir très précisément le détail de la démonstration et ce qu’on peut en tirer. Il est possible que cela soit intéressant en pratique, mais ce n’est pas assuré d’avance.
À propos de cryptographie
Dans l’épisode de la série, la preuve que P=NP inquiète un spécialiste de cryptographie. Il affirme que la démonstration rendrait obsolètes toutes les techniques de cryptage. Qu’en est-il vraiment ?
Il faut préciser qu’il existe des problèmes qu’on sait exponentiels, ni P ni NP. Donc les méthodes les utilisant ne sont pas liées à l’énigme P=?NP. De plus, la cryptographie utilise des problèmes réputés difficiles, mais pas nécessairement aussi difficiles que ceux dits NP-complets : c’est le cas par exemple de la factorisation liée au RSA. La confiance qu’on a en eux repose donc sur autre chose que sur l’hypothèse P ≠ NP. En réalité, la confiance qu’on a dans la plupart des protocoles de cryptographie courants provient de propriétés particulières démontrées, de l’expérience et principalement de la résistance aux attaques dont ils ont fait preuve. Les méthodes de sécurité en informatique ne sont donc pas directement liées à la conjecture P=?NP.
Dans cet épisode, la preuve que P=NP semble exploitée pour mener des intrusions informatiques dans le système de surveillance vidéo d’un bar. Un informaticien parvient à pirater le système informatique pour changer des dates sur des vidéos, afin de procurer un alibi. Il est peu probable qu’un tel piratage soit lié à la preuve que P=NP. D’ailleurs, le procureur chargé de l’affaire estime qu’en définitive, ce résultat n’aurait pas un impact si direct sur la sécurité des systèmes informatiques : elle ne provoquerait pas « le déclin inéluctable des techniques de cryptage modernes ». Cependant, on peut imaginer que disposer d’une telle solution pourrait aider indirectement à attaquer certaines méthodes de chiffrage.
À propos de la recherche en mathématique
L’épisode démarre par la découverte des meurtres de deux mathématiciens. Chez l’un deux, les murs d’une pièce, en apparence blancs, sont en fait couverts de symboles et schémas mathématiques, gardés secrets. Un mathématicien, appelé à la rescousse par les enquêteurs, essaie de leur communiquer son enthousiasme : il y a devant leurs yeux un début de démonstration que P=NP, rien que ça ! Si on regarde bien l’image, on y voit effectivement une mention de NP… Une mathématicienne, experte de la question, confirme : en étudiant ces formules, elle a compris que les calculs des mathématiciens assassinés avaient été plus loin que quiconque et qu’ils étaient très proches de la solution. Elle précise qu’ils n’avaient accompli que le tiers du travail.

Image extraite de l’épisode « Echec et Maths » de la série américaine Elementary créée par Robert Doherty, diffusée sur CBS depuis 2012, en France sur M6 depuis 2014.
Parvenir à cette conclusion est assez extraordinaire, pour au moins deux raisons. D’une part, ces calculs semblent quelque peu disparates, d’autre part résoudre le problème P=NP est un travail mathématique de démonstration. Or une démonstration ne repose pas principalement sur des calculs (au sens usuel et comme on en voit sur les tableaux montrés dans le film), mais sur des raisonnements, qui semblent totalement absents dans ce qu’on voit. Personne (et c’est vrai dans toutes les mathématiques) ne peut affirmer qu’une démonstration est faite au tiers. Tant qu’il manque quelque chose à une démonstration, il n’y a pas de certitude ! Vérifier la solution d’un problème mathématique difficile est un travail délicat, et pour le problème P=?NP ce sera le cas. Si une solution est proposée un jour de l’énigme P=?NP, il faudra un bon moment pour la valider.
Quelques points de détail sont amusants, au moins aux yeux de mathématiciens. L’enquêteur ouvre un exemplaire papier d’une revue scientifique, avec à l’intérieur une photo de tableau noir couverte d’équations. Cela lui permet de comparer l’écriture avec celle trouvée sur les murs. Or on ne publie pas une photo de tableau dans une revue scientifique, mais on rédige sur ordinateur les formules mathématiques, à l’aide d’outils spécialisés. On peut éventuellement imaginer qu’un magazine grand public publie une telle photo à la suite d’un reportage sur un scientifique prestigieux. On aurait aussi pu s’attendre à une lecture sur écran de la revue, en version dite électronique, même si des versions papier continuent d’exister.
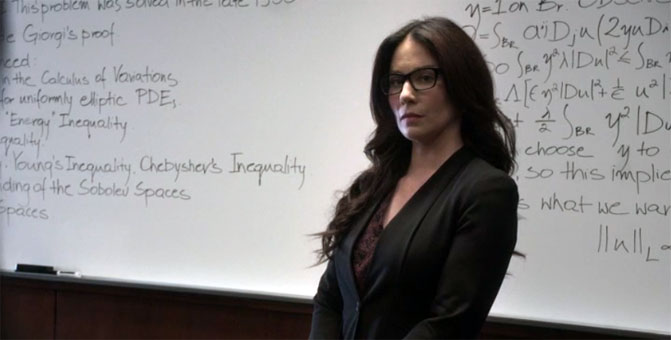
Image extraite de l’épisode « Echec et Maths » de la série américaine Elementary créée par Robert Doherty, diffusée sur CBS depuis 2012, en France sur M6 depuis 2014.
À la fin de l’épisode, les enquêteurs discutent avec l’experte du problème P=?NP. D’après le tableau derrière elle, cette mathématicienne travaille ou fait cours sur les équations aux dérivées partielles : on y voit le sigle PDE (Partial Differential Equations), des normes et des intégrales.
Les équations aux dérivées partielles (EDP) sont des équations fonctionnelles, dont les solutions sont des fonctions de plusieurs variables réelles.
La solution d’une équation algébrique est un ou plusieurs nombres. Ainsi les équations de la forme ax2 + bx + c = 0, qui implique le fameux trinôme étudié au lycée, possèdent, selon les valeurs des coefficients a, b et c, aucune, une ou deux solutions, c’est-à-dire des valeurs de x qui annulent le trinôme.
Une équation différentielle ordinaire (ODE) lie une fonction inconnue à ses dérivées. Ses solutions sont des fonctions d’une variable réelle. Par exemple, l’équation élémentaire f’(x) = a.f(x) admet comme solution la fonction f(x) = f(0) eax, puisqu’alors f’(x) = f(0) a eax, bien identique à a.f(x). Quand la variable x est le temps, les ODE décrivent des systèmes dynamiques, qui tentent de rendre compte de l’évolution de grandeurs au cours du temps, telles qu’une distance parcourue par un mobile, la tension aux bornes d’un circuit ou l’effectif d’une population.
Lorsque les grandeurs étudiées dépendent, outre le temps, de la position sur un axe, sur un plan ou dans l’espace, les fonctions impliquées possèdent autant de variables additionnelles. Ainsi, l’évolution de la température dans le temps et le long d’une tige métallique peut être modélisée par une fonction T (x, t), où x est la distance à l’extrémité de la tige et t est le temps écoulé depuis le début de l’expérience. Pour modéliser les phénomènes associés, il est nécessaire d’écrire des équations qui lient la fonction T (x, t) et ses dérivées par rapport à la variable t, mais aussi par rapport à la variable x : autant de dérivées dites partielles. La résolution numérique de ces équations sur un ordinateur permet de simuler l’évolution de la température en chaque point de la tige et au cours du temps.
Si les phénomènes évoluent dans un plan ou dans l’espace, ce sont de nouvelles variables y, puis z qu’il est ainsi nécessaire d’introduire, ainsi que les dérivées correspondantes dans les équations aux dérivées partielles. Ainsi, les prédictions météorologiques mettent en œuvre des modèles qui rassemblent des équations de la mécanique des fluides et permettent de simuler l’évolution dans le temps de grandeurs physiques telles que vitesse ou pression, et ce, à chaque point d’une grille tridimensionnelle au-dessus de la surface terrestre.
À côté de leur mise en œuvre pour la modélisation et la simulation de nombreux phénomènes, les EDP constituent un chapitre important des mathématiques pures.
Résoudra-t-on un jour l’énigme P=?NP à l’aide d’intégrales ou de normes ? Les doutes sont permis… Une chose est sûre, le mystère mathématique reste entier et le prix est toujours à gagner.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Jean-Paul Delahaye
Professeur émérite d'informatique à l'Université des Sciences et Technologies de Lille (Lille 1) et chercheur au Centre de recherche en informatique, signal et automatique de Lille (CRIStAL).