Sous le signe du calcul

Le mot « calcul » vient du latin calculus et rappelle l’utilisation de cailloux dans les procédures de comptage depuis au moins le IV^e millénaire avant notre ère. Des cailloux jetés dans un bol à l’entrée de la bergerie pour vérifier qu’il y avait autant de moutons qui rentraient le soir que d’animaux qui en étaient sortis le matin, aux bits dans la mémoire d’un ordinateur qui comptabilisent notre compte en banque, le chemin est long et il peut faire oublier que le calcul ne se résume pas aux opérations arithmétiques.

Compter, calculer, une histoire ancienne

Jusqu’au siècle dernier, les machines à calculer étaient principalement consacrées au calcul numérique : il s’agissait de simplifier le calcul de formules compliquées pour prévoir la position des étoiles ou de rendre routiniers les longs calculs nécessaires à la tenue des comptes. Cependant, l’Homme a très tôt imaginé des machines dont le rôle serait d’appliquer une procédure bien définie, on dit aujourd’hui un « algorithme », à autre chose que des nombres, pour produire la réponse à un problème.

Un exemple ancien est donné par les roues pivotantes de Raymond Lulle, au XIII^e siècle. Précurseur de la logique combinatoire, il inventa sous le nom d’Ars universalis une espèce de machine dialectique où les idées de genre étaient classées et distribuées. Le jeu des combinaisons de toutes les propositions possibles permettait d’énumérer automatiquement toutes sortes de raisonnements (cf. ci-dessous).

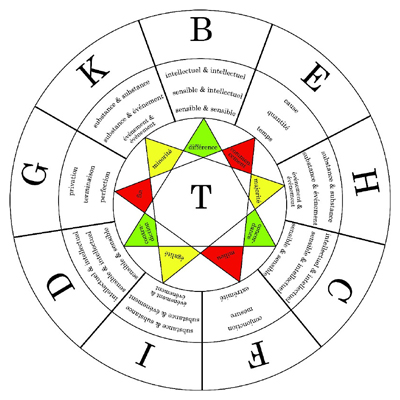
Reproduction de l’une des machines de Raymond Lulle. © A. Couty, CRDP de l’Académie de Versailles. Ce dessin représente une « machine à penser », une roue, imaginée au XIIIe siècle, dont le but était, grâce à ses deux anneaux mobiles, de mécaniser des raisonnements logiques. Par ce processus, on peut voir dans cet objet les prémices de l’informatique !

Plus tard, Leibniz, au XVII^e siècle, imaginait la construction d’une machine qui pouvait manipuler des symboles afin de déterminer les valeurs des énoncés mathématiques. En 1821, Charles Babbage présente à la Société royale britannique une « machine à différence ». Il veut automatiser le calcul des tables de logarithmes et des autres fonctions qui, à l’époque, sont élaborées manuellement et entachées d’erreurs. La machine est en constante évolution et entre 1834 et 1836, Babbage développe un nouveau modèle, la « machine analytique », qui comporte un dispositif d’entrée et de sortie, une mémoire intermédiaire, un dispositif pour transférer des nombres entre les différentes unités de la machine, etc.

Qu’est-ce qu’un calcul ?

Cette rapide évocation de quelques étapes historiques marquantes laisse cependant intacte la question : qu’est-ce qu’un calcul ? Une question qui attend une réponse urgente au début du XX^e siècle, en même temps que d’autres questions sur les fondements mêmes des mathématiques.

Dans les années trente, quatre mathématiciens au moins sont en lice pour répondre à cette question : Stephen Kleene, Alonzo Church, Alan Turing et Emil Post. Chacun veut définir une certaine notion du calcul. La quête va se révéler plus longue que prévue, mais les questions posées commencent à recevoir une réponse et c’est la naissance de la théorie de la calculabilité, qui vise à définir précisément ce qui est effectivement calculable. Alonzo Church est sans nul doute le premier à avoir pensé pouvoir définir formellement ce que l’on s’accorde à reconnaître intuitivement comme un calcul. En 1935, Stephen Kleene, son étudiant en thèse, formalise ce qu’est une « fonction arithmétique calculable » à travers la notion de « fonction récursive ». Alonzo Church essaie de capturer plus généralement l’idée de fonctions définies par des règles de calcul en développant un nouveau formalisme, le « lambda-calcul ».

Une machine sans conducteur

Alan Turing explore une autre approche, qui va lier la notion de « calcul » à la notion de « machine » : une machine qui peut fonctionner sans intervention humaine, une machine idéale qui n’a pas (encore) de réalisation physique, mais qui semble plausible. Cette machine possède un ruban, aussi long que nécessaire, sur lequel une tête de lecture/ écriture peut lire, écrire, effacer et réécrire des symboles pris dans un alphabet fini. La machine possède aussi un état interne et l’ensemble des états internes possibles est fini. Quand la tête lit un symbole, elle réagit en fonction de l’état interne en le modifiant, en réécrivant un symbole et en déplaçant éventuellement la tête vers la droite ou la gauche du symbole courant sur le ruban. Alan Turing justifie l’organisation et le fonctionnement de cette machine par analogie avec le travail d’un opérateur humain qui disposerait d’une mémoire propre très limitée, mais qui pourrait écrire des symboles sur une feuille de papier pour l’aider à dérouler un calcul. Au lieu d’écrire sur une surface, la machine écrit sur un ruban aussi long que nécessaire. Il apparaît clairement que cette machine abstraite peut réellement être construite.

Machine de Turing réalisée en briques LEGO ® par des étudiants en informatique. © Projet Rubens, Creative Commons (CC BY-SA). Cette construction est le résultat d’un défi relevé par huit étudiants : ils ont concrétisé une représentation de la machine qu’avait imaginée le mathématicien Alan Turing en 1936.

Alan Turing, le visionnaire

La machine de Turing est idéalisée car son fonctionnement réel a été abstrait ; par exemple, le ruban est supposé toujours suffisamment long (donc potentiellement infini). Alan Turing ne décrit pas une réalisation concrète de sa machine, alors même qu’un dispositif mécanique, pneumatique ou électrique pourrait la concrétiser. Il n’empêche, cette machine idéalise les ordinateurs d’aujourd’hui et, inversement, on peut voir dans les ordinateurs d’aujourd’hui une réalisation physique et électrique de la vision d’Alan Turing.

Alan Turing va appeler « nombre calculable » tout nombre qu’une machine peut écrire sur son ruban avant de s’arrêter. S’il n’existe pas de machine de Turing permettant de calculer une fonction donnée, on dit qu’elle n’est pas « Turing-calculable ». Plus généralement, un problème de décision est dit indécidable s’il n’existe aucun algorithme (aucun programme informatique) qui permette de le résoudre (sans restriction de mémoire ni de temps) à l’aide d’une machine de Turing. On peut définir très formellement des fonctions qui ne sont pas calculables. Par exemple, il n’existe pas de machine de Turing qui permette de répondre à la question de savoir si une machine de Turing quelconque va s’arrêter ou pas.

C’est en 1936 qu’Alan Turing publie sa définition de la calculabilité. Indépendamment, Emil Post propose une machine très similaire. Sa motivation est d’établir les limites fondamentales de la pensée humaine. Il suppose que les processus de pensée dont l’esprit humain est capable ne sont pas quelconques : ils sont finis et déterminés par des règles. Enfermés dans des règles (de calcul), il y a des problèmes que l’esprit ne peut résoudre (calculer). Ce rapprochement entre la pensée et le calculable n’est pas une préoccupation unique à Emil Post. Dans les années cinquante, Alan Turing proposera une procédure, le « test de Turing », pour déterminer si une machine fait preuve d’intelligence. Mais revenons aux machines de Turing.

Les secrets de la machine de Turing

© A. Couty, CRDP de l’académie de Versailles.

Chaque machine de Turing particulière correspond à un algorithme et l’état initial du ruban correspond aux « entrées » (on dit aussi « paramètres » ou « données ») de l’algorithme. Le comportement de la tête de lecture/écriture est dicté par l’unité de contrôle qui possède un état interne. L’état interne indique ce que doit faire la tête à la lecture d’un symbole donné sur le ruban : quel symbole doit-elle écrire, dans quelle direction doit-elle se déplacer, dans quel prochain état interne la machine doit-elle passer. Le résultat du calcul est l’état du ruban quand la machine s’arrête. Il est important de remarquer que le contrôle de la machine est fixé une fois pour toutes et s’identifie donc avec la machine elle-même. Une machine de Turing est une machine abstraite, mais s’il fallait la construire, le contrôle correspondrait à une structure fixe. La seule partie variable de la machine est constituée des symboles écrits sur le ruban qui peuvent changer au cours de l’exécution.

La machine à tout faire

Alan Turing prolonge alors ses travaux en établissant un résultat très surprenant : il existe une machine de Turing qui est dite « universelle » (MU) car elle est capable de « simuler » l’exécution de toutes les autres machines de Turing. Simuler une machine quelconque T veut dire ici que la machine universelle MU va se comporter comme la machine T si on lui fournit :

• la description du contrôle de T (en l’écrivant dans un certain format sur le ruban de MU) ;
• les données en paramètres du calcul (ailleurs sur le ruban de MU).

En particulier, quand MU s’arrête, elle laisse le ruban dans l’état où T l’aurait laissé à son arrêt. Autrement dit, elle réalise le calcul effectué par T.

Ce résultat est surprenant car il affirme qu’au lieu de considérer une variété infinie de machines différentes (des additionneurs qui font des additions, des multiplieurs qui font des multiplications, des horloges qui calculent la date et l’heure du jour, des astrolabes qui calculent la position des étoiles, des machines à calculer l’heure des marées, etc.), il suffit de considérer une seule machine qui peut faire tous les calculs, pourvu qu’on lui fournisse une description adéquate de la tâche à exécuter. Cette description, qui est une représentation du contrôle du calcul à effectuer, nous l’appellerons un « programme ».

Une invention révolutionnaire

Les conséquences de cette idée sont bouleversantes et ont véritablement transformé notre monde. La machine universelle ouvre la voie au développement des ordinateurs : au lieu de construire physiquement une machine différente pour chaque type de calcul, il suffit de construire une machine universelle et de lui donner le programme voulu sous la forme d’un état initial du ruban. Elle fera le même calcul que la machine spécialisée, elle ira sans doute un peu moins vite, elle utilisera sans doute un peu plus de mémoire (de longueur de ruban), mais elle arrivera au même résultat tout en évitant de construire autant de machines spécialisées qu’il y a de types de calcul à effectuer.

C’est ce qui a été fait : tous nos ordinateurs sont des machines universelles. Ce qui veut dire que quand vous achetez un ordinateur, vous n’avez pas besoin de préciser ce que vous voulez faire avec : le supercalculateur utilisé pour les prévisions météorologiques, votre ordinateur portable et le processeur embarqué dans votre lecteur de MP3 sont capables de faire les mêmes calculs. Bien sûr, ils ne le feront pas à la même vitesse ou la mémoire pourra être trop petite. Mais il n’y a pas de problème de principe. Et il est bien plus simple de construire une machine universelle et de la programmer que de construire une machine spécialisée différente pour chaque besoin.

Mon ordinateur, une machine universelle ?

Nos ordinateurs sont en fait un peu plus compliqués afin d’être plus efficaces. Alan Turing, qui a travaillé à la réalisation des premiers ordinateurs pendant et après la seconde guerre mondiale, l’avait prévu : déjà à l’époque, il indiquait que se déplacer de case en case sur le ruban était source d’inefficacité et qu’il fallait permettre de sauter d’une case à une autre case arbitraire grâce à une adresse (il faut numéroter les cases du ruban). On ne parle plus de ruban (d’une machine de Turing) mais de mémoire (d’un ordinateur). Cela ne change rien à ce que l’on peut calculer mais cela permet d’aller plus vite. Nos ordinateurs diffèrent aussi des machines de Turing en ce qu’ils n’ont pas à disposition une quantité arbitraire de mémoire. À chaque étape de son fonctionnement, la machine de Turing utilise un ruban de taille finie. Quand le calcul se termine, la machine n’a donc utilisé qu’une longueur finie de ruban. Mais cette longueur peut devenir arbitrairement grande et par exemple excéder les capacités mémoire de nos ordinateurs. Cela empêche de faire certains calculs, même si c’est théoriquement possible.

Calculs et symboles

La notion de calcul élaborée par Alan Turing est très souple : elle porte moins sur les objets du calcul que sur l’enchaînement des opérations, leurs itérations, leurs dépendances. Un ordinateur ne fait pas de différence entre calculer sur des nombres, sur des morceaux de musique (dans votre lecteur de MP3), sur des images (dans votre lecteur de DVD ou bien dans votre logiciel de retouche d’images) ou sur des mots (dans les moteurs de recherche et votre éditeur de texte). La nature des symboles manipulés n’intervient pas, ce qui importe c’est de manipuler des suites de symboles pris dans un ensemble fini.

Dispositif expérimental visant à développer un transistor fonctionnant avec un électron unique permettant de réaliser un qubit. « L’ordinateur quantique » soulève de nombreux défis. Même si pour le moment, le système n’est pas physiquement réalisé, théoriquement, ces super machines pourraient casser la plupart des codes cryptographiques, comme celui de la carte bancaire ! © Photo de Roy Kaltschmidt, Lawrence Berkeley National Laboratory.

Et c’est pourquoi, depuis Alan Turing, les chercheurs et les ingénieurs s’efforcent de trouver une représentation digitale, un « reflet numérique », à tous les objets du monde et de développer des convertisseurs d’un signal analogique en codage digital (capteurs) et d’un codage digital en un signal analogique (actionneurs) toujours plus performants pour relier et enchevêtrer le monde numérique et le monde physique.

La fin de l’histoire ?

L’existence d’une machine de Turing universelle ne répond pas à la question : est-ce qu’une machine de Turing peut calculer tout ce qu’on considère intuitivement comme calculable ? Il n’est pas exclu que l’on trouve un jour un système physique, matérialisant une procédure que tout le monde s’accorde à qualifier de « calcul », et qui ne puisse pas s’effectuer sur une machine de Turing. Depuis les années trente, de nombreux systèmes ont été proposés comme définition alternative de la notion de calcul, à commencer par les systèmes de Church et de Kleene. Mais, à chaque fois, on a pu montrer, soit qu’un système proposé n’était pas physiquement réaliste, soit, en produisant une traduction appropriée, que le système était équivalent à une machine de Turing. Les systèmes qui ont le même pouvoir d’expression sont dits « Turing-équivalents ».

Même si ces systèmes sont Turing-équivalents, la complexité des programmes peut être différente : on peut parfois calculer la même chose en moins de temps ou en utilisant moins de mémoire.

Par ailleurs, imaginer de nouveaux modes de calcul s’est révélé particulièrement fécond. Ainsi, en s’inspirant des processus biologiques, les informaticiens ont inventé de nouvelles méthodes d’optimisation (les algorithmes évolutionnistes), de nouveaux processus d’apprentissage (les réseaux de neurones) ou de nouvelles manières de piloter des robots. Dans un mouvement inverse, la notion de calcul a diffusé dans les autres sciences et a enrichi notre compréhension des processus physiques, biologiques et même cognitifs, à la lumière de concepts comme : information, mémoire, non-déterminisme, complexité, etc. L’héritage d’Alan Turing est là, bien vivant, et toujours à explorer.

Cet article est paru dans la revue DocSciences n°14 Alan Turing : La pensée informatique, éditée par le CRDP de l’Académie de Versailles en partenariat avec Inria.