Peut-on limiter les détours dans un réseau ?

De nombreuses situations peuvent être représentées par un graphe : un ensemble d’objets ou d’entités connectés par des liens ou des traits. Les graphes forment donc des réseaux d’entités. Certains d’entre eux, appelés graphes géométriques, modélisent des relations entre des objets ayant une propriété particulière : leur localisation dans l’espace. Par exemple, le graphe correspondant à une carte routière représente des villes et leurs connexions routières, et ces villes ont une géolocalisation, par exemple leurs coordonnées GPS. Les graphes géométriques représentent en général des relations de communication entre diverses entités ; à ce titre, ils doivent posséder diverses propriétés pour être considérés comme efficaces.

Des réseaux efficaces

Les réseaux dits « ad hoc » sont un exemple courant de graphes géométriques, dans lesquels les entités voulant communiquer, par exemple des ordinateurs ou des téléphones portables, ont une structure dite « auto-organisée ». À l’inverse des réseaux « classiques » de téléphonie ou de communication électronique dans lesquels il existe des points d’accès qui permettent de gérer les différentes routes, les entités du réseau ad hoc sont directement responsables de la création des routes de communication, ce qui peut être utile par exemple après une catastrophe naturelle ayant détruit les infrastructures de communication. Nous pouvons tirer de cet exemple plusieurs critères qui permettent de caractériser un graphe géométrique « efficace ». Les nœuds (ou entités) ont une localisation fixe et le but est de rajouter des connexions entre eux suivant plusieurs critères.

Le premier critère est évident : il faut pouvoir atteindre n’importe quel nœud du graphe depuis n’importe quel point de départ, c’est-à-dire que le graphe créé doit être connexe. Si cette condition n’est pas remplie, alors il existe des paires d’entités qui ne peuvent pas communiquer. Mais nous pouvons être plus exigeants et demander que dans le réseau, la distance entre deux nœuds ne soit pas trop éloignée de la distance à vol d’oiseau, ou « distance réelle ». Le rapport entre ces deux distances (qui est toujours au moins égal à 1) est naturellement appelé le détour entre ces nœuds dans le réseau. Afin qu’il n’y ait pas de mécontents, le plus grand des détours doit être le plus petit possible. La valeur du plus grand des détours est appelée étirement du réseau (voir figure 1 ci-dessous). Un t-spanner est un réseau dont l’étirement est inférieur à t.

Fig. 1 : Exemple de réseau géométrique. La distance dans le plan entre les points C et E est 5, alors que la distance dans le réseau entre ces deux points est 7, ce qui donne un détour de 7/5. Si on teste toutes les paires de points, on remarque que le plus grand détour est pour la paire (B, E) et vaut 4√2/4 = √2. Donc l’étirement du réseau vaut √2 ~ 1.41. Si l’on supprime l’arête AB, l’étirement monte alors à 4.37, car une communication entre A et B devra passer par les points D et C.

Évidemment, une manière de construire un réseau sans créer de détour est d’ajouter une route de communication entre chaque paire d’entités du réseau : le détour serait ainsi minimal, valant 1. Cependant, dans un réseau de communication, construire des routes ou maintenir des connexions a un coût. Il faudrait donc également minimiser le nombre total d’arêtes du réseau.

Un réseau ne possédant pas de croisement entre deux connexions est dit réseau planaire. Dans un réseau routier, tout croisement de connexions (donc de routes) nécessite la construction d’un pont, d’un tunnel ou d’un carrefour, et entraîne des coûts. De même, si un réseau ad hoc est planaire, alors il sera plus simple de calculer efficacement un chemin de communication plus court entre deux entités. Idéalement, le réseau construit devrait donc être planaire.

Dans la mesure du possible, il faudrait également éviter d’avoir des nœuds incidents ayant trop d’arêtes : maintenir des connexions avec un grand nombre de voisins a un coût (mémoire, bande passante, batteries, etc.) et certaines technologies imposent même un nombre maximum de voisins. Par exemple, un réseau de type « scatternet » est une juxtaposition de réseaux bluetooth (appelés piconets), chacun composé d’un nœud « maître » et d’au plus 7 nœuds « esclaves » voisins de celui-ci (sachant qu’un nœud peut être maître dans un réseau bluetooth au plus, mais qu’il peut être esclave dans plusieurs réseaux bluetooth). Si dans le réseau considéré, tous les sommets ont un degré inférieur à 7, il suffit de prendre comme ensemble de maîtres, un ensemble maximal indépendant — c’est-à-dire que chaque nœud est maître ou voisin d’un maître, et qu’il n’y a pas 2 nœuds maîtres voisins l’un de l’autre —, ce qui peut se faire efficacement et de manière distribuée.

Enfin, dans certains réseaux ad hoc, les nœuds du réseau sont mobiles, c’est-à-dire qu’ils changent de localisation au cours du temps. Il faut donc pouvoir calculer ou recalculer le réseau rapidement à partir des nœuds. Idéalement, ce calcul devrait pouvoir s’effectuer localement, c’est-à-dire que chaque nœud déciderait quelles seraient ses arêtes en fonction de la position des nœuds autour de lui.

Maintenant, faisons le point ! En résumé, un graphe géométrique « efficace » doit :

• avoir peu d’arêtes (au total) et peu de connexions autour de chaque nœud ;

• être planaire (les connexions ne se croisent pas) ;

• être un t-spanner, avec t le plus petit possible ;

• permettre de calculer / recalculer les connexions de façon simple et locale.

La question est alors la suivante : étant donné un ensemble P de nœuds, chacun avec une localisation, comment ajouter des arêtes entre ces nœuds pour créer un graphe géométrique, tout en garantissant le maximum de « bonnes » propriétés présentées ci-dessus ?

Construire des spanners efficacement

Dans la littérature, beaucoup de constructions différentes de graphes géométriques ont été proposées. Elles garantissent chacune des propriétés différentes parmi la liste que nous avons vue. Nous allons donc passer en revue quelques-unes des constructions de réseaux planaires les plus emblématiques et simples, et étudier leurs propriétés. Même si ces constructions ne sont pas forcément appliquées directement aux réseaux de communications — car d’autres contraintes que nous n’avons pas présentées ici peuvent apparaître —, ce sont des structures très étudiées faisant l’objet de nombreuses recherches.

La première construction est une structure appelée triangulation de Delaunay, proposée par le mathématicien russe d’origine française Boris Delaunay. C’est une construction très standard, élégante et simple à implémenter. Elle se génère à l’aide d’un petit test : pour chaque triplet de points (A,B,C) de l’ensemble de points P, on se pose la question suivante : « Est-ce que le cercle circonscrit au triangle (fictif) ABC contient d’autres nœuds de P ? ». Si la réponse est non — ce cercle est vide —, on ajoute les arêtes AB, AC et BC au réseau ; on dessine effectivement le triangle ABC. Si la réponse est oui — il y a au moins un sommet dans le cercle —, on ne fait rien. Au préalable, on aura également pris soin de s’assurer que dans l’ensemble de points P, aucun ensemble de trois points n’est aligné, et qu’aucun ensemble de 4 points n’est sur un même cercle. La figure 2 montre la construction de la triangulation de Delaunay d’un ensemble de points donné.

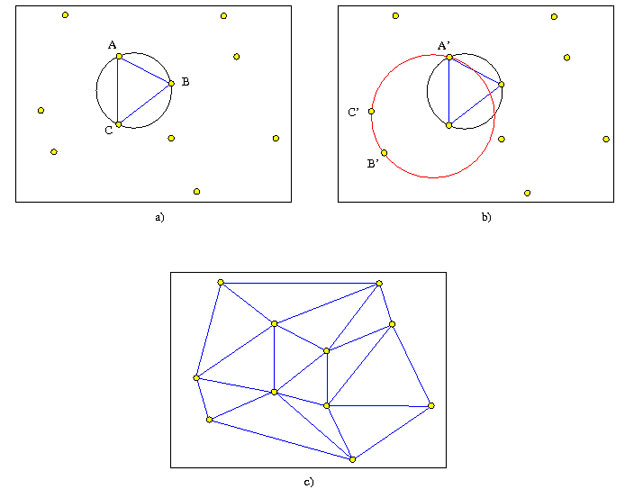
Fig. 2 : Construction d’une triangulation de Delaunay.
a) Le cercle circonscrit à A, B et C est vide, on dessine donc le triangle ABC.
b) Le cercle passant par A’, B’ et C’ n’est pas vide (il contient un point)donc on n’ajoute pas les arêtes de ce triangle.
c) Le résultat une fois tous les triangles construits.

Cet algorithme très simple produit un réseau planaire, dans lequel les nœuds ont en moyenne 6 voisins environ (d’après la formule d’Euler, un graphe planaire possède 3n-6 arêtes au plus et exactement 3n-3-k lorsque toutes les faces internes sont des triangles tandis que la face externe possède k sommets, donc le degré moyen du graphe est <= (6-6-2k)/n)

Par contre, les connexions ne sont pas calculées localement — il faut faire un test pour chaque triplet de points — et si les nœuds se déplacent ou sont retirés du réseau, un grand nombre de connexions peuvent être impactées. La propriété du réseau la plus difficile à caractériser est l’étirement.

En effet, de manière générale, analyser l’étirement des triangulations de Delaunay n’est pas chose aisée. La meilleure borne supérieure est de 1.998 ; autrement dit, pour tout ensemble de points P et toute paire de points (u,v) de cet ensemble, il existe un chemin de détour reliant u à v, valant au plus 1.998 dans la triangulation de Delaunay de P. À l’inverse, on peut trouver un ensemble de points dont la triangulation de Delaunay a un étirement de 1.58 (voir figure 3 ci-dessous). Cependant, déterminer plus précisément la valeur du pire étirement d’une triangulation de Delaunay — c’est-à-dire ici diminuer la valeur de l’étirement le plus grand ou trouver un ensemble de points créant un étirement de plus de 1.58 — est un problème largement ouvert et étudié.

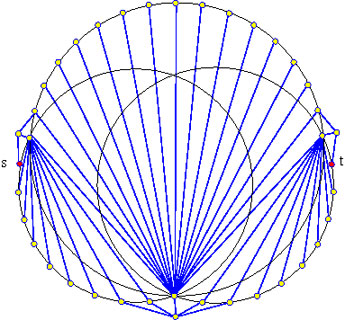
Fig. 3 : La triangulation de Delaunay (en bleu) de cet ensemble de points possède un détour de 1.58 pour aller du sommet s au sommet t.

Une seconde construction rencontrée fréquemment dans le domaine des réseaux géométriques est la construction dite du « Theta-graphe », proposée indépendamment par Clarkson et Keil à la fin des années 1980. Pour construire un Theta-graphe à partir d’un ensemble de points P, on commence par se fixer un paramètre entier k (par exemple k=6). Chaque point de P découpe alors le plan autour de lui en k secteurs égaux, et choisit un voisin dans chacun des secteurs pour ajouter une nouvelle arête au réseau (voir figure 4 ci-dessous). Le voisin choisi est le plus « proche », c’est-à-dire celui dont le projeté orthogonal sur la bissectrice du secteur est le plus proche du point central parmi tous les sommets présents dans ce secteur.

Pour la petite histoire, il existe des variantes des Theta-graphes, appelées graphes de Yao où le voisin choisi est le plus proche au sens de la distance Euclidienne, mais il n’est pas possible d’extraire simplement un spanner planaire des graphes de Yao, au contraire des Theta-graphes.

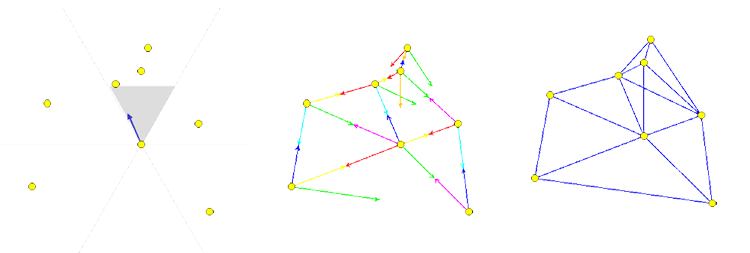
Fig. 4 : construction d’un Theta-graphe (ici avec k=6). Chaque sommet choisit un voisin pour chaque secteur non vide. Ici, le sommet du milieu possède 3 sommets dans son secteur nord et choisit le plus bas des trois.

Cette construction a l’avantage d’être assez simple à calculer et de s’effectuer de manière locale. En effet, chaque nœud de P peut effectuer l’analyse de son voisinage indépendamment, ce qui permet possiblement de paralléliser le calcul du réseau. De plus, elle garantit un étirement d’au plus \(\frac {1}{1 – 2 \sin (\pi/k)}\) pour k > 6. Par exemple pour k=7, l’étirement est de 7.56, pour k=8 l’étirement est de 4.26, et cet étirement reste supérieur à 2 pour k ≤ 12. Si on veut un étirement assez proche de 1, il suffit alors de prendre une valeur de k suffisamment grande, tandis qu’avec une triangulation de Delaunay, l’étirement sera supérieur à 1.58 pour certains ensembles de points (voir figure 3 ci-dessus). Enfin, le nombre maximal de connexions créées est connu : comme chaque nœud créera au plus k nouvelles connexions, il y a au plus k x n arêtes dans le réseau géométrique final. En contrepartie, le réseau construit n’est pas planaire comme on peut le constater sur l’exemple de la figure 4 (ci-dessus).

La dernière construction que nous allons présenter est le demi-Theta6-graphe, introduit en 2010. Cette construction se base sur le même principe que le Theta-graphe pour k=6, mais chaque nœud ne va considérer que 3 des 6 secteurs autour de lui : le secteur Nord, le secteur Sud-Est et le secteur Sud-Ouest (voir figure 5 ci-dessous). On peut colorer et orienter les arêtes : lorsque u choisit le sommet v, on oriente l’arête de u vers v ; colorons les arêtes du secteur Nord en bleu, et celles du Sud-Est et du Sud-Ouest respectivement en rouge et en vert.

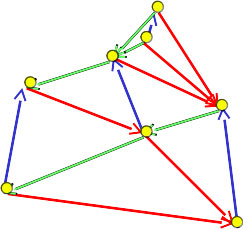
Fig. 5 : Exemple de demi-Theta6-graphe. Les arêtes des secteurs Nord sont en bleu, celles des secteurs Sud-Est sont en rouge et celles des secteurs Sud-Ouest en vert.

Cette fois, le nombre maximal de connexions n’est plus que de 3n : chaque nœud crée au plus 3 nouvelles connexions. La construction est toujours locale et simple car c’est une simplification de celle d’un Theta-graphe. Elle possède en outre deux propriétés remarquables : le réseau obtenu est planaire, et son étirement vaut au plus 2 (et cette borne sur l’étirement est atteinte, c’est-à-dire que l’on peut trouver un ensemble de points dont l’étirement du demi-Theta6-graphe calculé vaut exactement 2).

Planaire et degré borné

Parmi les critères que nous n’avons pas encore considérés dans les constructions précédentes, celui du degré maximum du réseau, soit le plus grand nombre de connexions incidentes à un même nœud, est souvent étudié. Les trois constructions précédentes garantissent un étirement borné, mais en revanche, rien n’est précisé sur le degré des sommets (voir par exemple la figure 4 ou la figure 6a (ci-après, en haut).

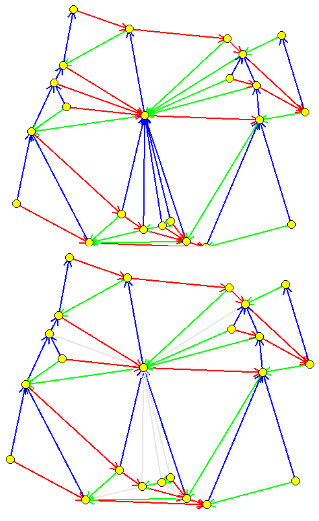
Fig. 6 : a) Un exemple de demi-Theta6-graphe avec un nœud possédant un grand nombre de voisins.
b) Une variante avec un degré borné par 12.

En se basant sur le demi-Theta6-graphe, on peut calculer facilement un réseau d’étirement et de degré bornés. Comme on peut le voir sur la figure 6a (celle du haut), le degré d’un sommet peut être arbitrairement grand, car il peut avoir un nombre arbitrairement grand d’arêtes entrantes dans les secteurs Sud, Nord-Ouest et Nord-Est. La stratégie pour borner le degré est de simplement garder pour chaque secteur Sud, Nord-Ouest et Nord-Est au plus 3 arêtes : celle vers le sommet le plus à gauche, celle vers le sommet le plus à droite et celle vers le sommet le plus proche. Ce faisant, chaque sommet possède au plus 3 x 3 arêtes entrantes et au plus, 3 arêtes sortantes. De plus, on peut montrer que l’étirement du réseau obtenu a évidemment augmenté puisque le nombre de connexions a diminué, mais qu’il est toujours borné : il est en fait d’au plus 6.

Actuellement, le meilleur résultat de ce type — trouver une construction de réseau géométrique planaire avec degré et étirement bornés — est une construction qui garantit un degré d’au plus 4 pour un étirement d’au plus 20. Il est clair que plus le degré maximal autorisé est petit, plus l’étirement obtenu sera grand. Par ailleurs, pour n’importe quelle constante C, il existe un nuage de points qui n’admet pas de réseau d’étirement au plus C et de degré maximal 2. On ne trouvera donc pas de résultat de ce type pour un degré maximal 2.

Il reste donc une question largement ouverte : existe-t-il une constante C telle que tout nuage de points P admette un réseau planaire d’étirement au plus C et de degré au plus 3 ?

Conclusion

Nous avons vu que les réseaux géométriques doivent posséder un certain nombre de caractéristiques (planarité, étirement borné, petit nombre de connexions, petit degré…) pour être dits « efficaces ». Le paramètre de l’étirement est le plus difficile à étudier, et malgré la simplicité des constructions présentées, l’analyse globale de leur étirement est complexe. Il y a donc encore beaucoup de travail pour espérer découvrir le réseau géométrique parfait !