De la transformée de Fourier à la transformée par ondelettes : le succès de l’analyse temps-fréquence
Les ondelettes, comme la décomposition de Fourier, sont des stars en analyse du signal. Cette discipline essaie d’étudier et de comprendre les signaux grâce aux mathématiques. Un signal est un mot large. Il peut être une fonction dépendant d’une variable, comme un ECG qui est une intensité électrique dépendant du temps. Ou encore, un signal peut être une image qui est une fonction couleur dépendant de deux variables indiquant la position du pixel.
Dans l’histoire des mathématiques, le succès a d’abord souri à la décomposition de Fourier, les ondelettes en étant en quelque sorte ses descendantes. En effet, depuis l’Antiquité on utilise les fonctions trigonométriques « cosinus » et « sinus » pour résoudre des problèmes géométriques. Au 18ème siècle, on commence à comprendre leur utilité en dehors de la géométrie. Et, plus précisément, vers 1810, Joseph Fourier énonce que toute fonction peut se décomposer comme une somme infinie de ces deux fonctions au moyen de calculs simples. Avec les années, les mathématiciens s’approprient ce résultat et les applications de celui-ci se multiplient. Son succès est implacable. Les ondelettes naissent bien plus tard, dans les années 1980, à partir de réflexions sur la décomposition de Fourier et grâce à l’avènement du numérique. Yves Meyer, l’un des pères fondateurs des ondelettes, reçoit le prestigieux prix Abel en 2017.
L’analyse par Fourier
Comme dit plus haut, la théorie de Fourier repose sur le fait que les fonctions montrant un certain degré de régularité peuvent être représentées par une somme infinie de sinus et cosinus, chacun multiplié par un nombre réel appelé coefficient. Celle-ci est bien expliquée dans l’article La décomposition en séries de Fourier dont une illustration est reprise ci-dessous.
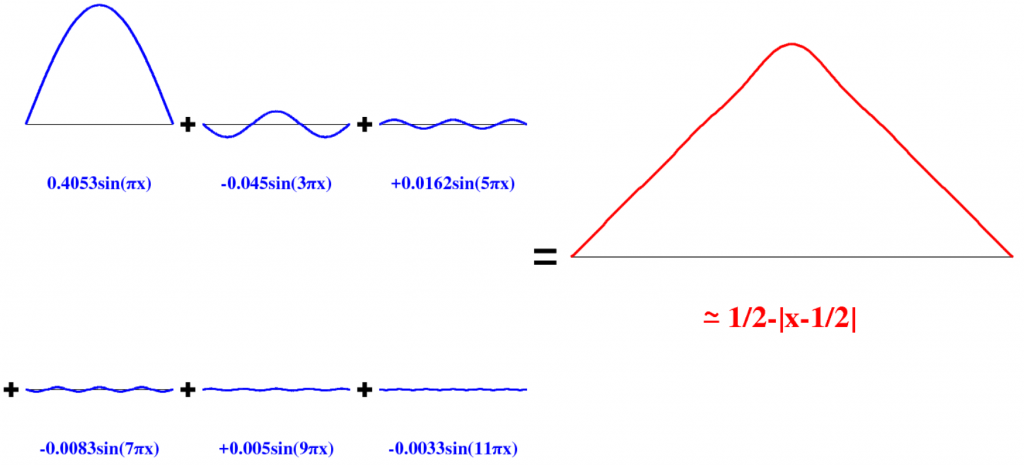
Décomposition de Fourier. Une fonction `f` est décomposée comme une somme de sinus, multipliés par un coefficient. (D’après La décomposition en série de Fourier.) Image © C. Charles
Les coefficients de cette somme, appelée combinaison linéaire, donnent une information au niveau des fréquences présentes dans le signal. En effet, dans la décomposition de Fourier de la fonction `f` ci-dessus, le grand coefficient devant `sin(pi x)` veut dire que dans la fonction `f` il y a beaucoup de fréquence égale à celle de `sin(pi x)`. A contrario, il y a peu de fréquence égale à celle de `sin(11pi x)` car le coefficient associé est petit. C’est la force de l’analyse par Fourier. En médecine, l’électrocardiogramme d’un patient malade diffère de celui d’un patient sain. Cette différence, parfois très difficile à repérer lorsque l’électrocardiogramme est donné en fonction du temps, devient évidente lorsque celui-ci est donné en fonction des fréquences, c’est-à-dire lorsqu’on regarde ses coefficients de Fourier.
L’analyse par Fourier est efficace, mais a ses limites
La transformée de Fourier donne la quantité de chaque fréquence présente dans le signal pour l’ensemble de la période d’observation. La théorie de Fourier devient donc inefficace pour un signal dont le spectre des fréquences varie considérablement dans le temps. La figure ci-dessous illustre ce problème: la transformée de Fourier d’une fonction `z(t)` composée d’un empilement de quatre contributions fréquentielles ressemblent à celui d’une autre fonction `y(t)` où ces contributions interviennent de manière isolée l’une à la suite de l’autre.
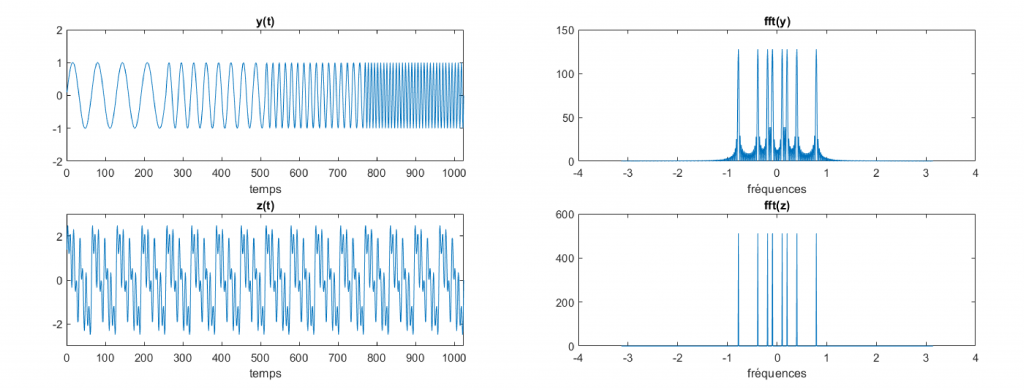
Les signaux \(y(t)\) et \(z(t)\) sont différents et leur transformée de Fourier est semblable. Les 4 grands pics se trouvent aux mêmes fréquences, ils correspondent aux 4 fréquences présentes dans \(y(t)\) l’un à la suite de l’autre et présentes dans \(z(t)\) simultanément tout au long du signal. Image © C. Charles
De plus, la transformée de Fourier est aussi utilisée pour approximer des fonctions. Certaines fonctions régulières ont une transformée de Fourier économique (ou parcimonieuse), autrement dit elles sont bien approximées avec peu de coefficients de Fourier non-nuls. Mais la transformée de Fourier ne fonctionne pas bien quand elle doit décrire localement une fonction qui montre des discontinuités, c’est-à-dire qui admet des sauts.
L’analyse par ondelettes
Les coefficients d’ondelettes sont dessinés dans une image et leur valeur est codée comme suit: bleu, vert et jaune pour les coefficients négatifs, nuls et positifs respectivement. L’axe horizontal représente le temps. L’axe vertical montre une quantité appelée la résolution (ou échelle); il correspond à la largeur du support temporel sélectionné par l’ondelette (voir l’article « L’analyse par ondelettes dans la vie de tous les jours »). Ceci veut dire que cela fonctionne comme pour une carte. Une grande échelle correspond à un grand support et donc à une vue globale non détaillée du signal et une petite échelle correspond à un petit support et donc à une vue détaillée d’une partie du signal. La résolution est souvent mieux comprise comme la réciproque de la fréquence. Ainsi une résolution fine (petite échelle) correspond à une haute fréquence et une résolution grossière (grande échelle) correspond à une basse fréquence. Souvent, dans un signal, ce qui est à petite échelle (et donc grande fréquence) apparaît de temps en temps comme des pics et ce qui est à grande échelle (et donc basse fréquence) est présent tout au long du signal. Dès lors, cette représentation temps-résolution donne de l’information temps-fréquence.
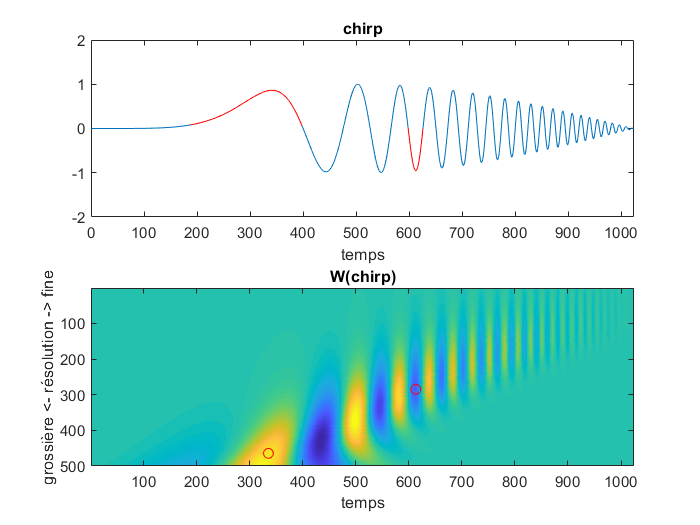
Interprétation des coefficients en ondelettes. En haut, le signal « chirp » fonction du temps. En bas, l’image de sa transformée en ondelettes. Image © C. Charles
Par exemple, comparons deux points de la transformée en ondelettes de la fonction « chirp » de la figure ci-dessus. On y voit un point jaune au temps 335 et à la résolution 465 et un point bleu au temps 613 et à la résolution 285. Le point jaune spécifie que la fonction varie dans un voisinage du temps 335 à une fréquence plus faible (car résolution plus élevée) que le point bleu qui a une fréquence plus élevée (car résolution plus faible). Le point bleu (coefficient négatif) spécifie que la fonction varie dans le sens opposé à celui du point jaune (coefficient positif). Le point jaune informe que la fonction varie dans un voisinage du temps 335, voisinage dont la taille est plus grande que le voisinage correspondant au point bleu au temps 613, car la résolution du point jaune 465 est plus grande que la résolution du point bleu 285.
Qu’apportent les ondelettes par rapport à l’analyse de Fourier ?
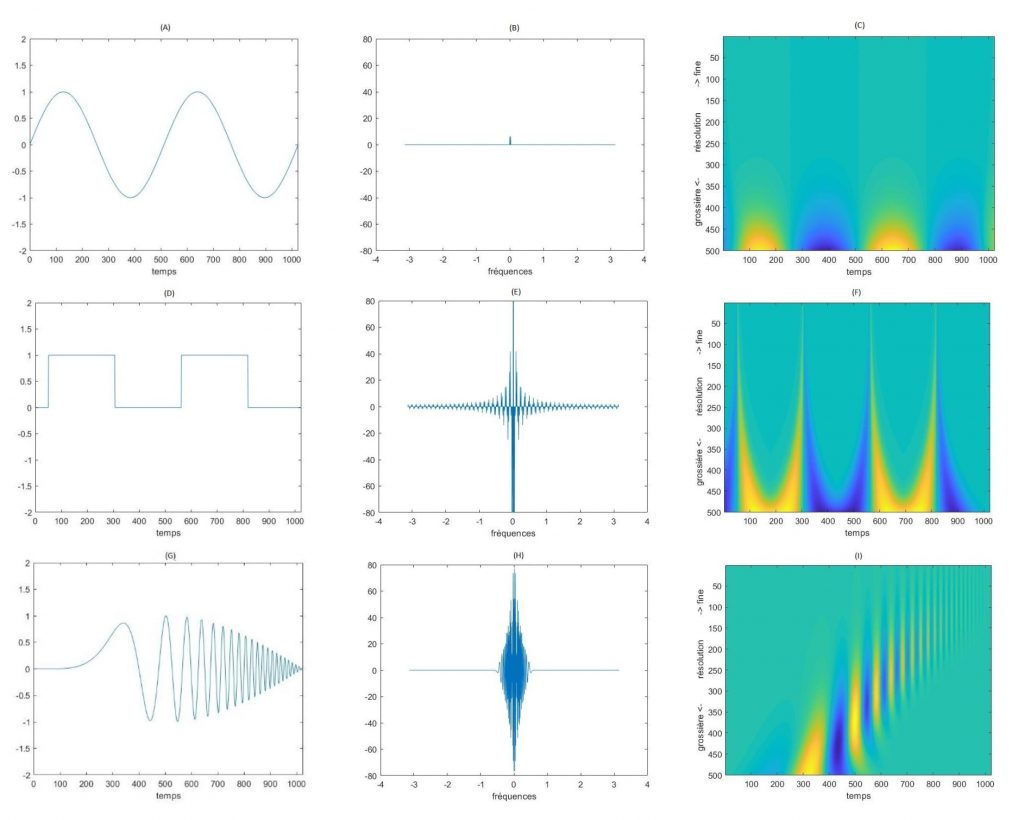
La colonne de gauche de la figure ci-dessous (d’après CHARLES, 2003) montre le graphe de trois fonctions (représentation temporelle): une fonction sinus en (A), une fonction « blok » en (D) et la fonction « chirp » en (G). La colonne du milieu ((B), (E) et (H)) montre les transformées de Fourier de ces fonctions (représentation fréquentielle). Finalement, la colonne de droite montre les transformées en ondelettes ((C), (F) et (I)). La même ondelette a été utilisée pour les trois fonctions.
Comparaison entre la transformée de Fourier et la transformée en ondelettes de trois fonctions. Image © C. Charles
En (A) la fonction sinus, en (B) sa transformée de Fourier et en (C) sa transformée en ondelettes. En (D) la fonction « blok », en (E) sa transformée de Fourier et en (F) sa transformée en ondelettes. En (G), la fonction « chirp », en (H) sa transformée de Fourier et en (I) sa transformée en ondelettes. L’axe des abscisses est le temps pour les fonctions, la fréquence pour les transformées de Fourier et le temps pour les transformées en ondelettes. L’axe des ordonnées pour la transformée en ondelettes est la résolution, souvent mieux comprise comme la réciproque de la fréquence. (D’après CHARLES, 2003)
Regardant la transformée en ondelettes de la fonction blok, on voit immédiatement qu’il y a des hautes fréquences dans les régions contenant des points anguleux, et seulement des zéros ailleurs. La transformée de Fourier montre certaines hautes fréquences mais ne donne aucune indication sur le moment où cela se passe. On peut aussi observer que les coefficients en ondelettes de la fonction sin et de la fonction blok se ressemblent à basse fréquence et deviennent très différentes quand la résolution devient petite. Notons aussi comment les transformées de Fourier des fonctions blok et chirp se ressemblent quelque peu, tandis que leur transformée en ondelettes donne une image différente avec plus d’informations. Toutes ces observations montrent la supériorité potentielle de la représentation en ondelettes par rapport à la transformée de Fourier.
Par contre, la fonction sinus peut être représentée par un seul coefficient de Fourier, ce qui n’est pas pris en compte par la transformée en ondelettes. Si un signal peut être exprimé comme une combinaison linéaire d’un petit nombre de sinus ou cosinus, l’analyse de Fourier restera plus efficace que les ondelettes pour des tâches telles que compression de données ou filtrage du bruit. D’un autre côté, la transformée en ondelettes des fonctions blok et chirp montre de nombreux coefficients nuls (en vert) indiquant une représentation économique de ces signaux. Ceci montre que les ondelettes sont une alternative à l’analyse de Fourier et non un remplacement.
En conclusion
La transformée en ondelettes offre la possibilité d’analyser un signal simultanément dans le domaine du temps et celui des fréquences. Est-ce intéressant? La réponse dépend de l’application et de la nature du signal. La transformée de Fourier d’un signal donné indique quelle quantité de chaque fréquence se trouve dans le signal mais ne nous indique pas à quel moment dans le temps ces fréquences se passent. L’information temps-fréquence n’est pas nécessaire quand le signal est stationnaire (signal dont le contenu de la fréquence ne change pas dans le temps) mais devient nécessaire pour un signal non-stationnaire.
Au restaurant, nous devenons rapidement insensibles au bruit de nos voisins; mais un brusque silence nous rappelle leur présence. Notre attention est attirée par les événements momentanés, par opposition aux phénomènes permanents que nous ignorons vite. La priorité accordée aux événements momentanés est probablement une stratégie de notre cerveau pour sélectionner les informations importantes, parmi le grand nombre de données auxquelles nous sommes exposés. La stratégie des ondelettes se base sur cette constatation.
Ainsi, par exemple, les ondelettes détectent facilement les contours des objets dans une image. Stocker « uniquement » cette observation permet de compresser l’image. C’est ce qui a donné naissance au format JPEG2000. Ensuite, l’information sur les contours dans une image est à l’origine même de la reconnaissance des empreintes digitales. Enfin, les ondelettes font facilement la différence entre un bruit présent partout sur une image et l’information présente dans l’image. Elles sont donc utilisées de manière efficace dans le débruitage. Pour en savoir davantage sur les applications des ondelettes, l’article L’analyse temps-fréquence dans la vie de tous les jours est disponible.
L’auteur remercie le comité éditorial d’Interstices pour lui avoir proposé le sujet d’article et pour leur relecture attentive. Les figures ont été réalisées avec MatLab.
- BITTON J. [2019]. Analyse multi-échelle de l’évolution des flux de chaleur sensible et latente échangés entre un écosystème forestier et l’atmosphère au moyen de la transformée en ondelettes continue. Master Thesis. ULiège.
- CHARLES C. [2003]. Some wavelet applications to signal and image processing. PhD Thesis. FUNDP.
- MALLAT S. [1988]. A wavelet tour of signal processing. Academic Press.
- STRANG G. [1993]. Wavelet transforms versus Fourier transforms. Bulletin (New Series) of the American Mathematical Society, 28:288-305.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Catherine Charles
Catherine Charles est membre de l'équipe BIODYNE et chargée de cours au sein du département Gembloux Agro-Bio Tech de l'Université de Liège.
