La machine à perspective de Jan van Eyck

Cet article est une version augmentée d’un article paru dans The Conversation le 16 aout 2021 : La véritable invention de Jan van Eyck

Jan van Eyck (c. 1390-1441) aura mis à rude épreuve les historiens de l’art soucieux de trouver une cohérence géométrique à sa manière de représenter l’espace. L’affaire semblait pourtant entendue dès 1905 : cette année-là, Karl Doehlemann démontrait dans un journal de mathématiques que les lignes fuyantes des Époux Arnolfini ne convergent pas vers un point de fuite unique, comme cela devrait être le cas dans une perspective linéaire, mais vers une zone circulaire de points de fuite : Jan van Eyck était un expérimentateur dont les « essais-erreurs » ont conduit de la perspective parallèle médiévale à une sorte de perspective empirique, décisivement différente de la solution mathématiquement correcte de Petrus Christus. L’interprétation de Doehlemann est aujourd’hui encore communément acceptée, mais une sorte de doute bergsonien a conduit en leur temps une poignée d’historiens de l’art à chercher un ordre caché derrière le désordre apparent des points de fuite des Époux.

Malheureusement, nous savons depuis Popper que toute activité d’observation est en proie au préjugé, et la nature même du désordre (nombre et positions des points de fuite à considérer) n’a pu faire l’objet d’un consensus.

Illustration dans le cas des Époux Arnolfini du biais introduit par le facteur humain dans les reconstructions de points de fuite. De gauche à droite : reconstructions proposées par J.G. Kern en 1912, J. Elkins en 1991 et P. H. Jansen et Z. Ruttkay en 2007

La solitude de James Elkins

Dans un article publié en 1991 dans la revue The Art Bulletin, l’historien d’art James Elkins déplore un manque d’objectivité et de reproductibilité dans les reconstructions de points de fuite consacrées aux Époux Arnolfini et entrevoit une échappatoire dans les méthodes informatiques naissantes « telles que la méthode des moindres carrés ». Il semble malheureusement qu’Elkins n’ait pas été entendu par les informaticiens spécialistes de vision par ordinateur dont il serait étonnant qu’un seul ait lu son article. La détection automatique de points de fuite a pourtant connu d’importants progrès depuis les années quatre-vingt-dix. Mais une peinture présente des difficultés propres, dont les algorithmes actuels, essentiellement conçus pour traiter des photographies, ne tiennent pas compte : les lignes fuyantes sont souvent plus limitées en nombre que dans une photographie, et leur représentation par le peintre ou leur extraction par le chercheur peuvent manquer de précision. Aussi les œuvres graphiques ne font-elles pas partie des bancs d’essai habituels de la communauté de la recherche en vision.

Une méthode probabiliste adaptée aux œuvres graphiques

Notre étude, présentée à SIGGRAPH en août 2021 et publiée dans la revue ACM in Computer Graphics and Interactive Techniques, tient compte de l’incertitude inhérente à la connaissance des lignes fuyantes et adopte un raisonnement probabiliste (pour la prise en compte des incertitudes) a contrario. Bien connues en vision par ordinateur, les méthodes a contrario sont inspirées de la théorie psychologique de la forme, et en particulier du principe de Helmholtz qui dispose que « nous percevons immédiatement [traduction mathématique : l’algorithme détectera] ce qui ne peut pas être dû au hasard ».

En appliquant le principe de Helmholtz à la carte probabiliste des points de fuite des Époux Arnolfini, nous obtenons une structure étonnamment ordonnée : quatre points principaux alignés périodiquement le long d’un axe vertical légèrement incliné. Des structures similaires sont obtenues dans d’autres tableaux de Jan van Eyck : Saint Jérôme dans son étude, La Vierge de Lucques, La Vierge de Dresde et La Vierge dans une église. Chacun de ces tableaux peut être partitionné en autant de bandes horizontales qu’il y a de points de fuite, chaque bande regroupant l’ensemble des arêtes associées au même point : les perspectives de Jan van Eyck sont rigoureusement exactes, par morceaux.

À gauche : carte de probabilité des points de fuite. À droite : application de la méthode a contrario à cette carte de probabilités. Gilles Simon, Université de Lorraine

Appliquons la méthode a contrario au portrait des Arnolfini : à gauche, la carte de probabilité des points de fuite tenant compte d’une incertitude sur les extrémités des arêtes extraites (visibles en rouge dans l’image de droite). À droite, l’application de la méthode a contrario à cette carte de probabilités. Les arêtes extraites sont reliées au point de fuite correspondant, la couleur du lien traduisant sa consistance : du bleu foncé au jaune clair pour une consistance allant respectivement de 0 à 1. Les arêtes se regroupent par bandes horizontales, délimitées ici par des lignes blanches.

Une précision diabolique

Reconstruction des points de fuite dans La Vierge dans une église. Gilles Simon, université de Lorraine

Le cas de la Vierge dans une église est particulièrement intéressant. Dans ce tableau presque aussi petit qu’une miniature (14 x 31 cm), la précision des traits au regard de leur convergence est extrême.

Mais le plus étonnant est que les positions des points de fuite obtenus dans la bande supérieure du tableau sont parfaitement cohérentes avec la géométrie en demi-décagone du chœur de l’église. Cela est inattendu, car personne ne pouvait savoir à cette époque comment placer un point de fuite sur la ligne d’horizon en fonction de la direction des lignes qui l’ont engendré. La seule explication possible est que Jan van Eyck utilisait un dispositif optique à travers lequel il représentait l’espace, en superposant méticuleusement ses traits à la réalité.

Une « machine à perspective » préfigurant la Réalité Augmentée…

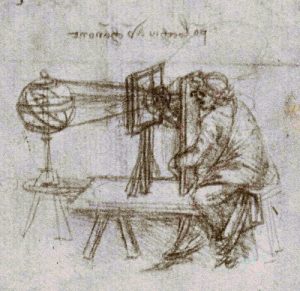
Léonard de Vinci, vers 1480. Détail du Codex Atlanticus, Wikimedia

Près d’un demi-siècle après la mort de Jan van Eyck, Léonard de Vinci dessinera une version simplifiée de cette « machine à perspective ».

Dans le dessin de Léonard, le peintre trace les contours des objets visibles à travers une vitre, le regard immobilisé derrière un œilleton. Plus élaboré, le dispositif de Jan van Eyck comportait quatre œilletons répartis équitablement (à l’instar des points de fuite) le long d’un axe de visée incliné (une droite selon laquelle sont alignés les œilletons). Le Maître « décalquait » la réalité bande après bande, œilleton après œilleton, en utilisant une sorte d’encre de Chine qu’il transférait ensuite sur un panneau de bois préalablement apprêté (Jan van Eyck est contemporain de l’invention de l’imprimerie). Il pouvait alors peindre à sa guise, en s’appuyant plus ou moins sur le dessin préparatoire ainsi réalisé.

La vitre pouvait elle-même être déplacée dans son plan, afin de raccorder au mieux, compte tenu de la parallaxe, le bord de la bande précédemment dessinée à la réalité perçue depuis l’œilleton suivant (voir l’animation vidéo). Cette étape cruciale permettait au peintre d’obtenir des transitions douces entre les bandes, difficilement décelables à l’œil nu. De surcroît, elle anticipait de plusieurs siècles le principe de la réalité augmentée. Dans ce domaine, nous cherchons en effet également à superposer des images générées par ordinateur (l’équivalent du dessin sur la vitre) à la réalité.

… utilisée depuis la position assise jusqu’à la position debout

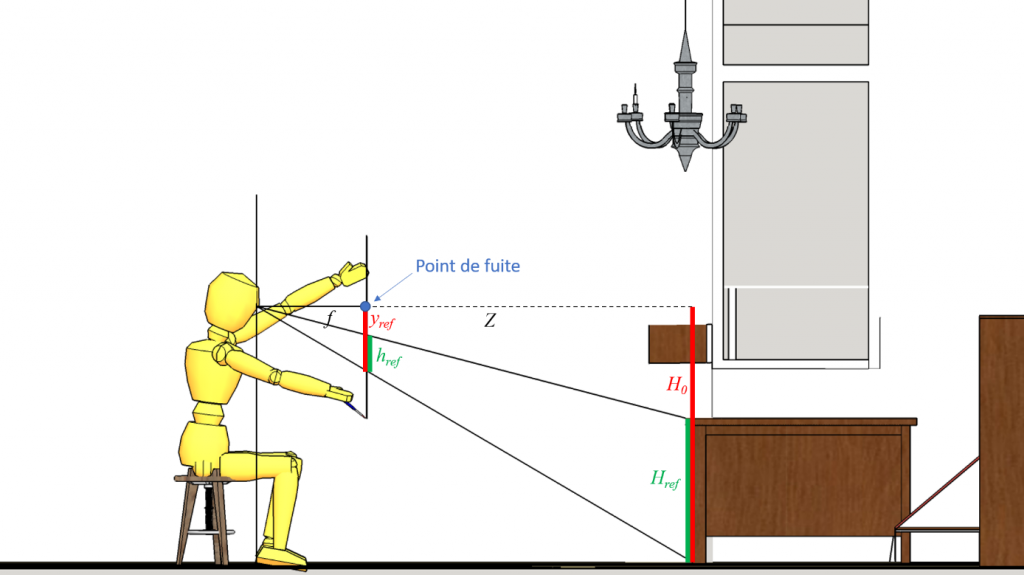
Une simple application du théorème de Thalès permet de reconstruire en trois dimensions la chambre des Arnolfini et le dispositif optique. Par exemple, l’illustration ci-dessous montre comment la hauteur de l’œilleton le plus bas, ainsi que la profondeur (la distance à l’œilleton) du meuble situé sous la fenêtre, peuvent être calculées connaissant la distance entre l’œilleton et la vitre (appelée distance de vue, elle peut être obtenue grâce à la présence du vitrail dans le tableau) et la hauteur du meuble (estimée à 65 cm par des chercheurs de l’université de Twente, Pays-Bas).

© Gilles Simon

Utilisation du théorème de Thalès pour retrouver la hauteur \(H_0\) de l’œilleton du bas et la profondeur \(Z\) du meuble, connaissant la distance de vue \(f = 49,7\) cm, la hauteur du meuble dans la réalité \(H_{ref} = 65\) cm, la hauteur du meuble dans le tableau \(h_{ref} = 16,4\) cm et la distance verticale dans le tableau entre le point de fuite du bas et la base du meuble \(y_{ref} = 29,5\) cm. D’après le théorème de Thalès nous avons, d’une part, \(Z/f = H_0/y_{ref}\) (1) où \(Z\) et \(H_0\) sont les inconnues du problème et, d’autre part, \(Z/f = (H_0-H_{ref})/(y_{ref}-h_{ref})\) (2). En regroupant (1) et (2), nous obtenons \(H_0/y_{ref} = (H_0-H_{ref})/(y_{ref}-h_{ref})\), c’est-à-dire \(H_0=y_{ref} \times H_{ref}/h_{ref} = 116,9\) cm. Connaissant \(H_0\),nous pouvons déduire de (1) que \(Z=f \times H_0 / y_{ref} = 196,9\) cm.

Le théorème de Thalès permet ainsi d’obtenir une reconstruction en trois dimensions de la chambre des époux et du dispositif optique, dont nous pouvons déduire que Jan van Eyck mesurait 1 m 77 et qu’il a commencé à dessiner la scène en position assise pour la terminer en position debout. La distance entre l’axe de visée et la vitre était d’environ 50 cm, ce qui lui permettait d’atteindre les coins du tableau avec son pinceau, tout en gardant l’œil derrière les œilletons. Giovanni Arnolfini mesurait 1 m 75, Giovanna son épouse, 1 m 66. Le peintre (plus exactement son œil) se trouvait à 1 m 50 des époux, et à 2 m 30 du mur situé derrière lui (visible dans le miroir convexe). En regardant le tableau, le spectateur se retrouve donc lui-même au milieu de la pièce, entre les époux Arnolfini et les deux étranges personnages visibles dans le miroir, dont l’un pourrait bien être Van Eyck lui-même.

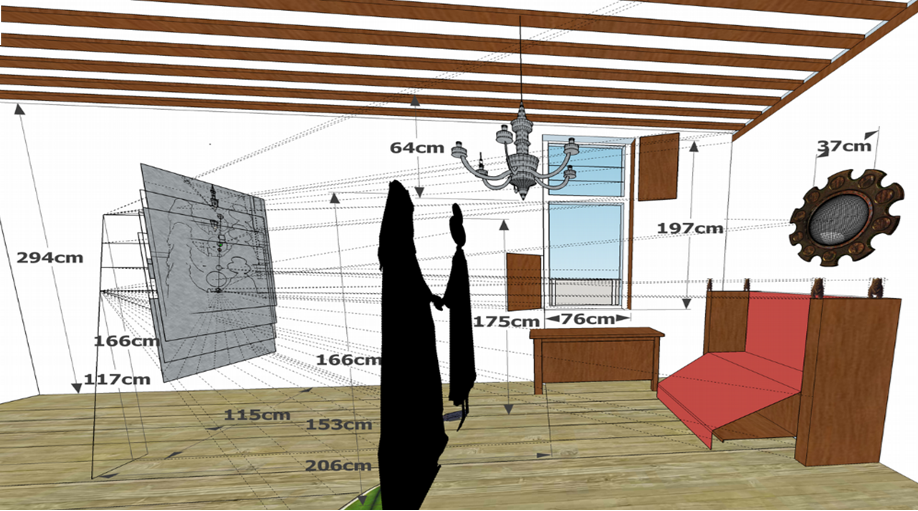
Reconstruction en trois dimensions de la chambre des époux Arnolfini et du dispositif optique. Gilles Simon, Université de Lorraine

Au plus près de la perception humaine

Reconstruction de l’exécution du portrait des Arnolfini. Gilles Simon, université de Lorraine

En haut : Postures du peintre au cours de l’exécution. En bas : vues obtenues depuis les quatre œilletons. Le dessin sur la vitre est représenté en noir et blanc, avec en plus clair le dessin préparatoire et en grisé le dessin à l’encre de Chine qui sera transféré sur le panneau apprêté, par dessus lequel Jan van Eyck peignait à l’huile, la réalité est en couleur.

Notre reconstruction 3D permet également de simuler ce que Jan van Eyck voyait à travers les œilletons. Nous pouvons ainsi par exemple observer la montée du plafond entre la vue du bas et celle du haut finalement retenue pour le plafond (et inversement pour le sol) : Jan van Eyck semble avoir été soucieux d’éviter les « déformations latérales ».

L’amplification des déformations perspectives sur les bords du tableau n’est pas incorrecte du point de vue de l’optique, mais nous n’y sommes pas habitués parce que le champ visuel de l’œil humain est plus réduit que celui atteint dans une perspective artificielle à courte distance, ou à travers une vitre lorsque le peintre s’autorise à rouler des yeux et à se contorsionner pour élargir son champ visuel immédiat. Il est probable que Jan van Eyck ne se satisfaisait pas de ces effets inhabituels, et qu’il ait préféré peindre à l’état naturel de repos les objets situés en face de lui, quitte à relever son tabouret en cours d’exécution et à terminer debout pour atteindre l’ensemble de l’espace visible.

Prise en compte de la vision binoculaire ?

L’inclinaison de l’axe de visée n’a sans doute pas été laissée au hasard, dans la mesure où elle était évidente à l’œil nu et compliquait le raccordement des bandes. Pour le portrait des Arnolfini, la distance horizontale entre les œilletons situés aux extrémités de l’axe de visée était égale à la distance interpupillaire d’un homme adulte. D’où cette impression de voir un anaglyphe (c’est-à-dire un dessin destiné à être vu en relief, grâce à des lunettes 3D) dans le dessin sous-jacent des Époux, obtenu par réflectographie infrarouge. Chacun décidera s’il s’agit d’une coïncidence, mais l’auteur de ces lignes parierait que non. Il imagine Jan van Eyck fermant alternativement l’œil gauche et l’œil droit, observant les effets de cette action sur la perception de sa propre main et décidant de doter son dispositif des deux options.

Des chercheurs de la National Gallery ont souligné, à propos du portrait des Arnolfini, combien la représentation des mains et des pieds était importante à cette époque, à la fois sur le plan symbolique et sur le plan esthétique. Si la plupart des objets n’ont été dessinés qu’une seule fois depuis l’œilleton le plus frontal, le dessin sous-jacent montre que la main levée et les pieds de Giovanni ont été redessinés depuis d’autres œilletons. Les deux dessins de la main et les trois dessins des pieds sont décalés spatialement en raison de la parallaxe, mais les subtils raccords de Jan van Eyck permettaient qu’ils ne le soient pas trop. Ce dernier pouvait donc retenir, au moment de peindre, l’une ou l’autre des déclinaisons.

Genèse

Les autres parties du corps de Giovanni ont également été dessinées plusieurs fois, et le partitionnement du tableau en bandes d’épaisseurs différentes suggère que Jan van Eyck a focalisé son attention sur quatre régions d’intérêt : le plafond, la tête coiffée de Giovanni, sa main levée et le bas du corps. Un soin particulier semble donc avoir été apporté au portrait du commanditaire, plus encore qu’au cadre architectural. Et ainsi, le dispositif polyscopique de Jan van Eyck pourrait bien être le fruit de l’évolution d’un dispositif monoscopique (équivalent à celui dessiné par Léonard) concomitante à la nécessité de réaliser un portrait en pied (peut-être Adam dans le retable de Gand) après avoir réalisé des portraits en buste. Il ne s’agit là que d’une première hypothèse, qui mériterait d’être confrontée à d’autres. Encore faudrait-il que notre article ne connaisse pas le même sort que celui d’Elkins, en sens inverse.