L’autostabilisation ou comment un système distribué peut se réparer tout seul

Le concept d’autostabilisation

Peut-être aimez-vous à retrouver dans votre lit, après une journée harassante, votre oreiller à mémoire de forme ? Ces oreillers contiennent généralement du polyuréthane qui leur permet de reprendre leur forme originelle après qu’on s’est amusé à les plier dans tous les sens. Nous allons voir dans la suite que l’oreiller à mémoire de forme peut être compris comme une allégorie de l’autostabilisation, un concept fondamental de l’algorithmique distribuée qui est, grosso modo, l’algorithmique dédiée aux réseaux informatiques. Pour cela, détaillons un exemple illustratif. Considérons un programme \(\mathcal P\) contenant une unique variable entière (strictement) positive \(v\). Cette variable est initialisée de manière quelconque (au hasard, par exemple). Le code de \(\mathcal P\) consiste à appliquer itérativement l’algorithme suivant :


si v est paire, divisons v par deux

sinon multiplions v par trois puis ajoutons-lui un.

Observons maintenant une exécution de notre programme, c’est-à-dire l’évolution dans le temps de son état, une photographie du système à un instant donné. Ici, l’exécution correspond à la suite des valeurs prises par \(v\). Par exemple, si nous fixons la valeur initiale de \(v\) à 12, on obtient la séquence infinie

Nous pouvons remarquer que \(s\) est composée du préfixe \(12, 6, 3, 10, 5, 16, 8\) suivi de la répétition infinie du facteur \(4, 2, 1\). Essayons une autre valeur initiale pour \(v\), disons 29. On obtient alors la séquence infinie

Là encore, après un nombre fini d’itérations, \(s’\) boucle successivement sur les valeurs \(4\), \(2\), puis \(1\). Jusqu’à maintenant, ce phénomène de boucle a été observé sur toutes les valeurs initiales (entières positives) testées. Cependant, bien que l’énoncé de ce problème soit somme toute assez simple, il n’existe toujours pas de preuve démontrant que ce phénomène est inéluctable quel que soit l’entier positif choisi pour initialiser \(v\). Cette question ouverte est connue sous le nom de « conjecture de Syracuse ». Le célèbre mathématicien Paul Erdös dira d’ailleurs à son propos que les mathématiques ne sont pas encore prêtes pour de tels problèmes. Revenons à notre système. Son état consiste simplement en la valeur de la variable \(v\). L’ensemble des états possibles du système est l’ensemble des entiers positifs \(\mathbb N^+\). Afin de caractériser le phénomène de boucle, divisons l’ensemble des états possibles en deux :

• le sous-ensemble \(\{1,2,4\}\), que l’on appellera ensemble des états légitimes et qui est lié au comportement attendu à terme de notre système ;
• ainsi que son complémentaire, \(\mathbb N^+ \setminus \{1,2,4\}\), que l’on appellera ensemble des états illégitimes.

On peut alors reformuler la conjecture de Syracuse comme suit : est-il vrai que le programme \(\mathcal P\) vérifie les deux propriétés suivantes :

• Convergence : quel que soit l’état initial du système (ici, quelle que soit la valeur entière positive initiale de \(v\)), l’exécution de \(\mathcal P\) atteint en temps fini un état légitime ;
• Correction : à partir de tout état légitime, l’exécution de \(\mathcal P\) réalise le comportement attendu. (Dans le cas de Syracuse, le comportement attendu est que 1 est suivi de 4, 4 suivi de 2 et 2 suivi de 1.)

Pour résumer, notre programme \(\mathcal P\) est-il autostabilisant ? En effet, un système est dit autostabilisant s’il existe un ensemble d’états légitimes pour lequel le système vérifie les propriétés de convergence et de correction, étant donné un comportement attendu appelé spécification. Notre exemple introductif permet aussi d’illustrer une notion fondamentale en autostabilisation : le temps de stabilisation. Le temps de stabilisation dans une exécution donnée est la longueur du préfixe maximum contenant uniquement des états illégitimes, par exemple pour \(s\) le temps de stabilisation est de \(7\). Plus généralement, le temps de stabilisation d’un système est égal au maximum des temps de stabilisation de toutes ses exécutions.

Un premier algorithme

Contexte : les systèmes distribués tolérants aux pannes

Originellement, l’autostabilisation a été définie par Edsger Wybe Dijkstra dans le contexte des systèmes distribués. Un système distribué est un ensemble d’entités de calcul (typiquement des ordinateurs), généralement appelées processus, qui sont à la fois autonomes et interconnectées entre elles. Le but de ces entités est de coopérer afin de résoudre une tâche globale à l’ensemble du système.

Par « autonome », il faut comprendre que chaque processus est pourvu de son propre contrôle, d’une mémoire privée et qu’il n’existe a priori aucun mécanisme sous-jacent de synchronisation des processus tel que l’accès à une horloge globale, par exemple. Ainsi, chaque processus exécute son programme à un rythme qui lui est propre.

Par « interconnectées », nous entendons l’existence d’un réseau de liens de communication sous-jacent permettant aux processus d’échanger de l’information directement avec tout ou partie des autres processus. Là encore, les échanges d’information se réalisent de manière asynchrone. Par exemple, si deux processus essaient de communiquer simultanément avec un troisième, on ne sait a priori pas quelle communication sera traitée en premier.

Bien que la notion de panne ne soit pas explicite dans la définition des systèmes autostabilisants, la motivation première de cette approche est pourtant la tolérance aux pannes, qui qualifie l’aptitude d’un système à résister à ou récupérer — sans intervention extérieure (humaine par exemple) — des pannes survenant sur une partie de ses composants (processus ou lien de communication). Il peut s’agir, par exemple, de pertes de messages, de corruptions de mémoire ou encore d’arrêt sur défaillance de processus.

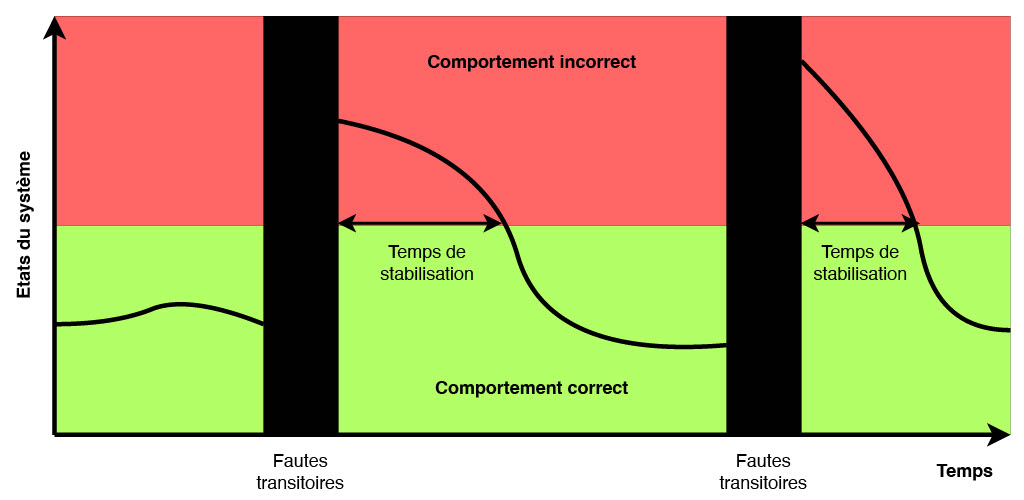
Figure 1 : Tolérance aux pannes transitoires d’un système autostabilisant.

Comme illustré dans la figure 1 ci-dessus, un système autostabilisant tolère naturellement les pannes dites transitoires, c’est-à-dire des perturbations temporaires et rares du fonctionnement de certains de ses composants (liens de communication ou processus), à condition que celles-ci ne modifient pas le code des processus (ce qui peut être garanti, entre autres, en stockant le code dans la mémoire morte (ROM) du processus, qui est une mémoire non réinscriptible). À titre d’exemple, les corruptions de mémoire, comme la modification non prévue de quelques bits de la mémoire d’un serveur (pourquoi pas suite à une surchauffe temporaire de celui-ci), sont généralement considérées comme des pannes transitoires.

Les pannes transitoires ont une durée finie mais perturbent l’état du système au moment où elles interviennent. Ainsi, après de telles pannes, on peut à juste titre considérer que l’état du système est quelconque. Or, les pannes transitoires sont, par définition, rares. Donc, il est raisonnable de penser que le temps entre deux perturbations transitoires est suffisamment grand pour permettre au système de retrouver de lui-même un état légitime à partir duquel il réalisera la tâche pour laquelle il a été conçu — c’est-à-dire sa spécification — pendant très longtemps ; précisément jusqu’à l’apparition de nouvelles pannes. Bien entendu, afin de maximiser la période de bon fonctionnement du système, les recherches en autostabilisation se sont surtout concentrées sur la conception d’algorithmes autostabilisants efficaces en temps de stabilisation.

Le problème : la circulation de jeton

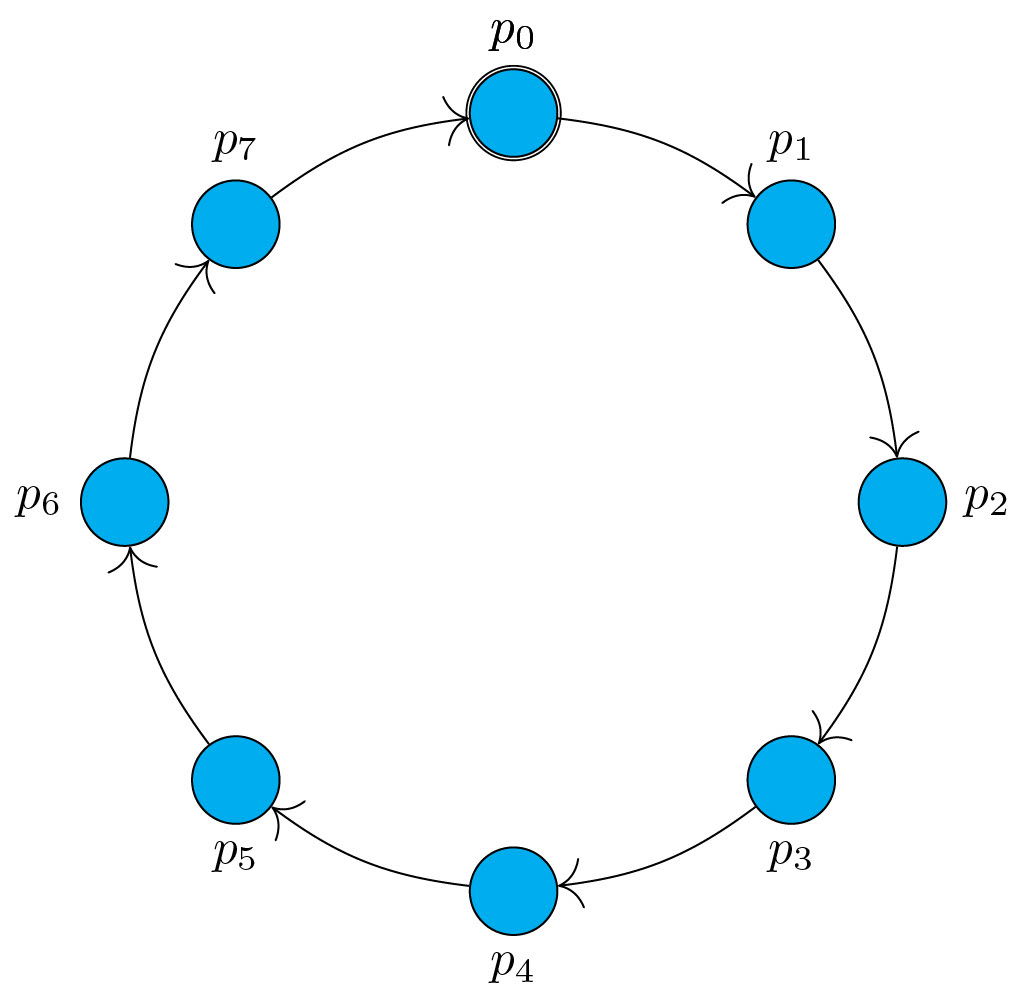
Figure 2 : Anneau unidirectionnel enraciné en \(p_0\).

Pour illustrer le concept d’autostabilisation, le mathématicien et informaticien néerlandais Dijkstra a proposé trois algorithmes autostabilisants de circulation de jeton dans un modèle haut niveau appelé « modèle à états ». Nous allons maintenant présenter le premier d’entre eux, donc le tout premier algorithme autostabilisant de l’Histoire.

Cet algorithme suppose un réseau d’une topologie particulière : il s’agit d’un anneau unidirectionnel et enraciné de \(n\) processus, \(p_0, \ldots, p_{n-1}\) (cf. figure 2 ci-dessus). « Unidirectionnel » signifie que l’information circule dans un seul sens, ici le sens des aiguilles d’une montre. Plus précisément, il existe un lien unidirectionnel de \(p_i\) à \(p_{(i+1)\bmod n}\), pour tout \(i\) dans l’intervalle \([0..n-1]\) : \(p_i\) est ainsi le prédécesseur de \(p_{(i+1)\bmod n}\) dans l’anneau. Autrement dit, chaque processus peut obtenir de l’information uniquement de son prédécesseur dans l’anneau. Par ailleurs, « Enraciné » indique que tous les processus sauf un sont identiques. Ici, le processus distingué, appelé racine, est le processus \(p_0\) : le code de l’algorithme de la racine sera différent de celui des autres processus.

Dans un anneau unidirectionnel, une mesure importante est la distance entre deux processus, c’est-à-dire le nombre d’arcs à traverser, dans le sens des flèches, pour aller de l’un à l’autre. Par exemple, dans l’anneau unidirectionnel donné dans la figure 2 ci-dessus, il faut traverser 5 arcs pour aller de \(p_1\) à \(p_6\) : \(p_1\) est à distance 5 de \(p_6\). En revanche, il faut traverser 3 arcs pour aller de \(p_6\) à \(p_1\) donc \(p_6\) est à distance 3 de \(p_1\). Le but de cet algorithme est de permettre au système de converger depuis un état quelconque, où il y a potentiellement zéro ou plusieurs jetons, vers un état légitime à partir duquel un unique jeton circule dans le réseau et visite chaque processus infiniment souvent.

Le premier algorithme de Dijkstra

Description de l’algorithme

Pour cet algorithme, chaque processus \(p_i\) (y compris la racine) dispose d’une unique variable entière notée \(p_i.v\) dont le domaine est l’intervalle \([0..K-1]\), où \(K\) est n’importe quelle valeur supérieure ou égale au nombre de processus \(n\) dans l’anneau. Les variables sont supposées localement partagées : chaque processus \(p_i\) peut lire sa variable \(p_i.v\), ainsi que celle de son prédécesseur. En revanche \(p_i\) peut uniquement écrire dans \(p_i.v\). Les communications point à point seront réalisées uniquement par le biais de ces variables partagées.

Le principe de l’algorithme est simple. La racine incrémente sa variable modulo \(K\) lorsque celle-ci est égale à celle de son prédécesseur. Les autres processus se contentent de recopier la variable de leur prédécesseur lorsque cette dernière a une valeur différente de la leur.

Le programme de chaque processus est donné sous la forme d’une règle gardée unique. Pour \(p_0\), la règle est la suivante :

Pour les autres processus \(p_i\) (avec \(i \in[1..n-1]\)), la règle est la suivante :

La condition entre le « si » et le « alors » est appelée la garde de la règle. Dans un état donné, un processus est dit activable si la garde de sa règle est vraie. Par exemple, dans la figure 3 ci-dessous, les processus \(p_0\), \(p_2\), \(p_3\), \(p_5\) et \(p_6\) sont activables.

Figure 3 : Anneau enraciné unidirectionnel initialisé avec un état quelconque (\(K=8\)).

La sémantique de l’algorithme est simple : un processus détient un jeton uniquement lorsqu’il est activable. Pour rappel, à partir d’un état quelconque, l’algorithme doit faire converger le système vers un état légitime à partir duquel un unique jeton circulera dans le système. Ici, l’ensemble des états légitimes consistera simplement en l’ensemble des états où un seul processus est porteur d’un jeton, c’est-à-dire qu’un seul processus est activable.

Propriété : l’absence d’interblocage

On peut tout d’abord montrer l’absence d’interblocage : dans chaque état du système, au moins un processus est activable, c’est-à-dire qu’au moins un processus détient un jeton. Pour cela nous utilisons un raisonnement par l’absurde, c’est-à-dire que l’on démontre que le contraire est impossible. Ainsi, supposons un état où aucun processus (en particulier \(p_0\)) n’est activable. Cela signifie, entre autres, que la garde de la règle de chaque processus non racine est fausse. On en déduit alors que la variable de chaque processus non racine est égale à celle de son prédécesseur. Par transitivité, on obtient \(p_0.v = p_{n-1}.v\). C’est une contradiction puisque, dans ce cas, \(p_0\) est activable : \(p_0.v = p_{n-1}.v\) est la condition d’activation de la règle de \(p_0\) (observez par exemple l’état 6 de la table 1 ci-dessous comme illustration de cette contradiction). Ainsi, l’hypothèse de départ du raisonnement par l’absurde disant qu’il existait un état où aucun processus n’était activable est fausse : dans chaque état, au moins un processus est activable, c’est-à-dire qu’au moins un processus détient un jeton.

Table 1 : Une exécution séquentielle avec \(K=8\). Les cases coloriées en vert indiquent les processus activés lors de la prochaine étape de calcul. Les cases en jaune correspondent aux processus activables de l’état qui ne sont pas activés lors de la prochaine étape de calcul.

Ce résultat préliminaire est principalement dû au fait que la règle de la racine \(p_0\) est différente de celles des autres processus. Il est très important dans la suite. En effet, il signifie que tant que le système n’est pas dans un état légitime, il contient nécessairement plusieurs jetons. Par exemple, dans l’état donné en figure 3, il y a cinq jetons (\(p_0\), \(p_2\), \(p_3\), \(p_5\) et \(p_6\) portent un jeton). Ainsi, le but de l’algorithme est de supprimer des jetons jusqu’à ce qu’il n’en reste qu’un seul.

Exécutions de l’algorithme

Une exécution de ce système consiste en une suite infinie d’états \(e_0, \ldots, e_i, \ldots\) où (1) \(e_0\) est quelconque (c’est-à-dire que chaque variable \(p_i.v\) a une valeur quelconque prise dans \([0..K-1]\)) et (2) où, à chaque instant \(i > 1\), l’état à cet instant, noté \(e_i\), est obtenu en modifiant \(e_{i-1}\), qui est l’état à l’instant précédent, par l’application simultanée de la règle activable d’un à plusieurs processus activables dans \(e_i\).

Le choix parmi les processus activables n’est volontairement pas fixé : cela matérialise l’aspect asynchrone du système. Ainsi, il existe de nombreuses exécutions possibles du système et le but est de démontrer que le système stabilise quelle que soit l’exécution. Par exemple, lors de la première étape à partir de l’état donné en figure 3, le choix est effectué parmi les 31 sous-ensembles non vides de \(\{p_0, p_2, p_3, p_5, p_6\}\), l’ensemble des processus activables initialement.

Dans les tables 1 et 2, nous donnons deux préfixes d’exécution possibles à partir de l’état initial donné dans la figure 3. Les lignes correspondent aux états atteints. Nous donnons en vert la liste des processus activés lors de la prochaine étape de calcul ; nous représentons en jaune les processus activables non activés.

Considérons, par exemple, l’état 2 dans la table 1. Les processus activables (en jaune et vert) sont \(p_2\), \(p_3\) \(p_5\) et \(p_6\), mais seul \(p_2\) (en vert) est activé lors de la transition vers l’état 3 : seul \(p_2\) exécute sa règle qui consiste à recopier la valeur 7 de la variable de son prédécesseur \(p_1\). En prenant la valeur 7, \(p_2\) devient inactivable et rend aussi inactivable \(p_3\). Donc, dans l’état 3, seuls \(p_5\) et \(p_6\) sont encore activables, \(p_5\) sera activé lors de la prochaine étape de calcul, etc.

Notez que dans l’exécution donnée en table 1, un seul des processus activables exécute sa règle à chaque étape. Cette exécution stabilise en quatre étapes. En effet, le premier état légitime est l’état 4 : dans cet état il y a bien un seul processus porteur du jeton (c’est-à-dire un seul processus activable, en vert), le processus \(p_6\). L’exécution donnée dans la table 2 ci-dessous est synchrone : à chaque étape, tous les processus activables exécutent leur règle. Elle stabilise en 11 étapes. En effet, le premier état légitime est l’état 11 : dans cet état il y a bien un seul processus porteur du jeton (c’est-à-dire un seul processus activable, en vert), encore une fois le processus \(p_6\).

Table 2 : Une exécution synchrone avec \(K=8\). Les cases coloriées en vert indiquent les processus activés lors de la prochaine étape de calcul.

Nous insistons sur le fait que ce sont deux exécutions particulières : la stabilisation du système doit être démontrée pour toutes les exécutions, y compris les exécutions où des sous-ensembles de processus activables de tailles différentes sont activés à chaque étape.

Un exemple d’exécution plus erratique du 1^er algorithme de Dijkstra est visible dans la vidéo ci-dessous. 

La preuve, ou pourquoi ça stabilise ?

La question fondamentale à traiter maintenant est pourquoi ce système est autostabilisant ? Pour cela, il faut se convaincre que le système vérifie les propriétés de convergence et de correction pour le problème de la circulation de jeton et l’ensemble d’états légitimes défini précédemment, c’est-à-dire l’ensemble des états où il existe un unique porteur de jeton.

Propriété de correction

Considérons tout d’abord la propriété de correction : il faut montrer qu’à partir de tout état légitime, le jeton reste unique et visite infiniment souvent chaque processus de l’anneau.

Avant de démontrer cette propriété, observons le comportement de l’algorithme à partir d’un état légitime. Par exemple, regardons le déroulement de l’exécution présentée dans la table 2 ci-dessus à partir de l’état 11. Nous remarquons alors trois cas caractéristiques :

1. L’unique porteur de jeton est le prédécesseur de la racine, comme dans l’état 12. Dans ce cas, sa valeur (0 dans l’état 12) est différente de celles de tous les autres processus, qui ont par ailleurs la même valeur (1 dans l’état 12). L’unique porteur de jeton exécute alors sa règle et le système se retrouve dans un état où tous les processus ont la même valeur (1 dans l’état 13), ce qui correspond au cas suivant.
2. L’unique porteur de jeton est la racine (cf. l’état 13). Dans ce cas, la racine incrémente sa valeur modulo \(K\) et le système se retrouve dans le cas suivant.
3. L’unique porteur de jeton \(p\) n’est ni la racine ni son prédécesseur (cf.  les états 11, 14 et 15). Dans ce cas, il y a uniquement deux valeurs présentes dans le système. La première (par exemple, 2 dans l’état 15) couvre les processus allant de la racine au prédécesseur de \(p\) et la seconde (par exemple, 1 dans l’état 15) couvre les processus allant de \(p\) au prédécesseur de la racine. La première valeur est alors propagée à chaque étape un cran de plus vers la droite jusqu’à ce que le système se retrouve à nouveau dans le premier cas.

De ces différentes observations, on déduit la preuve suivante. Par définition, dans un état légitime quelconque \(\gamma_i\) il y a un seul processus activable \(p\). Celui-ci exécutera nécessairement sa règle lors de l’étape suivante, de l’état \(\gamma_i\) à l’état \(\gamma_{i+1}\). Donc, seul \(p\) va modifier sa variable lors de cette étape. De plus, puisque la garde de la règle de chaque processus dépend uniquement de sa variable \(v\) et de celle de son prédécesseur, l’activation de \(p\) ne peut influencer que \(p\) et son successeur dans l’anneau. Ainsi, on est sûr que les autres processus ne détiendront toujours pas de jeton dans \(\gamma_{i+1}\). De plus, puisque seul \(p\) modifie son état, on peut remarquer que l’exécution de sa règle (qu’il soit racine ou pas) rend fausse la garde de sa règle. Ainsi, \(p\) ne détient plus de jeton dans \(\gamma_{i+1}\). Donc seul le successeur de \(p\) peut détenir le jeton dans \(\gamma_{i+1}\). Or, nous avons montré précédemment (cf., l’absence d’interblocage) qu’il existait au moins un porteur de jeton dans chaque état. Donc, le successeur de \(p\) détient nécessairement l’unique jeton dans \(\gamma_{i+1}\) : l’unique jeton a été transféré de \(p\) à son successeur. Ainsi, un unique jeton circule infiniment souvent parmi tous les processus : la propriété de correction est vérifiée.

Propriété de convergence

Nous rappelons que la propriété de convergence énonce qu’à partir d’un état initial quelconque, le système atteint en temps fini un état légitime, ici un état où un seul processus est porteur d’un jeton.

Résultat intermédiaire

La propriété de convergence est basée sur le résultat intermédiaire suivant : la racine \(p_0\) exécute sa règle infiniment souvent.

Ce résultat se démontre par l’absurde. On suppose donc, par l’absurde, que la racine \(p_0\) n’exécute sa règle qu’un nombre fini de fois. Ainsi, il y a un certain état \(\gamma_0\) à partir duquel la racine n’exécute plus jamais sa règle.

On observe alors le phénomène suivant. Considérons un processus activé \(p\) (donc \(p\) n’est pas la racine). Soit il transmet son jeton à son successeur (comme le jeton qui passe de \(p_1\) à \(p_2\) dans la huitième et dernière étape de l’exécution donnée dans la table 1), soit son jeton disparaît avec parfois celui de son successeur ; cf. les jetons de \(p_2\) et \(p_3\) dans l’état 2 de la table 1 disparaissent dans l’état 3 ou encore le jeton de \(p_5\) dans l’état 3 de la table 1 disparaît dans l’état 4.

Ainsi, après chaque étape à partir de \(\gamma_0\), la somme \(S\) des distances entre les porteurs de jeton non-racine et la racine diminue strictement. Pour rappel, \(p_i\) est un porteur de jeton non-racine si \(i \neq 0\) (ce n’est pas la racine \(p_0\)) et la variable de \(p_i\) a une valeur différente de celle de son prédécesseur dans l’anneau (ce qui signifie que \(p_i\) détient un jeton).

Par exemple, lors de la troisième étape de l’exécution donnée dans la table 1, c’est-à-dire lors de la transition de l’état 2 à l’état 3, cette somme passe de 16 à 5. En effet, dans l’état 2, 4 processus non-racines détiennent un jeton : \(p_2\), \(p_3\), \(p_5\) et \(p_6\). Or,

• \(p_2\) est à distance 6 de la racine \(p_0\) car pour aller de \(p_2\) à \(p_0\) en suivant l’orientation des flèches il faut aller en \(p_3\), \(p_4\), \(p_5\), \(p_6\), \(p_7\) et enfin \(p_0\),
• \(p_3\) est à distance 5 de la racine \(p_0\),
• \(p_5\) est à distance 3 de la racine \(p_0\) et
• \(p_6\) est à distance 2 de la racine \(p_0\).

Ce qui donne au total \(S = 16\). Dans l’état 3, seuls deux processus non-racines portent encore un jeton : \(p_5\) et \(p_6\), qui sont respectivement à distance 3 et 2 de la racine \(p_0\). Ainsi, dans l’état 3, \(S\) vaut \(5\).

Lorsque la somme \(S\) atteint zéro, aucun processus non racine ne détient un jeton et ainsi seule la racine est activable (NB : nous avons montré qu’il n’existe pas d’état sans porteur de jeton, cf. l’absence d’interblocage). Donc, elle exécute nécessairement sa règle lors de l’étape suivante, ce qui est contradictoire car nous avions déduit qu’à partir de \(\gamma_0\) la racine n’exécuterait plus jamais de règle. Ainsi, l’hypothèse de départ de notre raisonnement par l’absurde est fausse, ce qui signifie que le contraire est vrai : la racine exécute sa règle infiniment souvent.

Notez que l’argument principal de la preuve sur la décroissance de \(S\) est connu sous le nom de variant ou fonction de potentiel. Ce type de raisonnement est couramment utilisé dans les preuves d’autostabilisation.

Conclusion de la preuve

Nous savons maintenant que la racine \(p_0\) exécute infiniment souvent sa règle. Or, cette règle a pour effet d’incrémenter \(p_0.v\) modulo \(K\). Ainsi, \(p_0.v\) passe par toutes les valeurs de son domaine (infiniment souvent). Or, puisque seule la racine peut introduire de nouvelles valeurs dans le système (les autres se contentent de recopier des valeurs existantes) et que le domaine de \(p_0.v\) contient au moins \(n\) valeurs (\(K\) est supérieur ou égal à \(n\), le nombre de processus), le système finit nécessairement par atteindre un état \(\gamma\) où la valeur \(x\) de \(p_0.v\) est unique dans tout le système (voir, par exemple, l’état 6 dans la table 2 où la valeur 1 n’est présente qu’en \(p_0\)). À partir de cet état \(\gamma\), la prochaine fois que \(p_0\) sera activable (et nous venons de démontrer que cela arrivera), tous les processus auront la même valeur : l’état sera légitime car dans ce cas seule la racine \(p_0\) détiendra un jeton (voir, par exemple, l’état 13 dans la table 2). L’explication de ce phénomène est la suivante. Pour que \(p_0\) redevienne activable à partir de \(\gamma\), il faut que son prédécesseur \(p_{n-1}\) prenne pour valeur \(x\). Or, puisque seule la racine détient la valeur \(x\) dans \(\gamma\), pour que cela arrive, il faut que \(x\) soit recopiée successivement par \(p_1\), \(p_2\), … jusqu’à \(p_{n-1}\). De plus, après avoir recopié \(x\) dans sa variable, un processus non-racine \(p_i\) ne pourra pas changer sa valeur tant que la racine ne l’aura pas changée elle-même en exécutant sa règle. Ainsi, un état où seule la racine détient un jeton finit par être atteint : la convergence est assurée et nous pouvons conclure que l’algorithme réalise une circulation de jeton autostabilisante.

Le temps de stabilisation

Une dernière question fondamentale est l’efficacité de l’algorithme. Le temps de stabilisation en nombre d’étapes de calculs de cet algorithme a été étudié de manière très précise. Il a été démontré que dans le pire des cas, la convergence nécessite exactement \(\frac{3n(n-1)}{2}-n-1\) étapes si \(n \geq 4\), 3 étapes si \(n=3\), et 0 étape sinon. Un exemple de pire des cas pour un anneau de cinq processus (c’est-à-dire 24 étapes de calcul) est donné dans la table 3 ci-dessous.

Table 3 : Une exécution pire des cas dans un anneau de 5 processus. Ici, \(K\) est n’importe quelle valeur supérieure ou égale à 5. Les cases coloriées en vert indiquent les processus activés lors de la prochaine étape de calcul. Les cases en jaune correspondent aux processus activables de l’état qui ne sont pas activés lors de la prochaine étape de calcul.

Algorithme autostabilisant pour le calcul d’un arbre couvrant

Le contexte : les systèmes à passage de messages

L’exemple précédent est conçu pour une topologie très particulière ainsi qu’un modèle haut niveau, le modèle à états. Cet exemple est donc assez éloigné des réseaux réels où la topologie est généralement assez irrégulière et où les communications sont réalisées par passage de messages. Notez toutefois qu’il existe des techniques pour faire fonctionner efficacement dans le modèle à passage de messages un algorithme écrit initialement dans le modèle à états.

Nous allons maintenant nous intéresser à un problème plus pratique ainsi qu’à une solution autostabilisante à ce problème fonctionnant directement dans le modèle à passage de messages. Il faut noter que dans ce type de systèmes, un état initial quelconque signifiera que non seulement les états des processus, mais aussi ceux des liens de communication, seront quelconques. Ainsi, initialement, chaque variable de chaque processus aura une valeur quelconque prise dans son domaine de définition (par exemple, une variable entière contiendra n’importe quel entier) et chaque lien de communication contiendra un nombre fini mais arbitraire de messages assignés avec des valeurs quelconques (ce qui matérialise le fait que les pannes transitoires peuvent aussi toucher les liens de communication en modifiant leur contenu).

Nous considérons maintenant un réseau de \(n\) processus à la fois connexe, c’est-à-dire un réseau où il existe un chemin reliant chaque paire de ses processus, et bidirectionnel, ce qui signifie que, pour chaque lien, la communication est possible dans les deux sens. Deux processus seront dit voisins s’ils sont connectés par un lien. Chaque processus distinguera localement chacun de ses liens de communication incidents par un numéro unique. Ce dernier est généralement nommé numéro de port. Par « localement », nous signifions qu’un lien entre un processus \(p_i\) et un processus \(p_j\) pourra avoir un numéro différent chez \(p_i\) et \(p_j\). Par exemple, dans le réseau représenté à gauche dans la figure 4 ci-dessous, le lien entre \(p_0\) et \(p_1\) a le numéro 0 chez \(p_0\) et 2 chez \(p_1\).

Le problème : la construction d’un arbre couvrant

Dans un réseau, une tâche courante consiste à collecter régulièrement des informations en un processus particulier, généralement appelé puits. Pour permettre d’effectuer cette tâche, il peut être intéressant de calculer en préambule un arbre couvrant orienté vers le puits, c’est-à-dire un sous-ensemble de \(n-1\) arêtes du réseau orientées de façon à décrire, pour chaque processus, l’unique chemin élémentaire (c’est-à-dire sans répétition de lien) de l’arbre le menant au puits. Ainsi, les informations à transmettre au puits pourront être routées le long des chemins de l’arbre. Nous allons maintenant nous pencher sur le problème du calcul d’un arbre couvrant d’un réseau enraciné en un processus \(p_0\) : \(p_0\) sera le puits de l’arbre. Un exemple d’un tel arbre est donné dans la figure 4 ci-dessous.

Figure 4 : À droite nous donnons un arbre couvrant enraciné en \(p_0\) du réseau représenté à gauche.

Bien entendu, il ne s’agit pas de stocker la description complète de l’arbre couvrant dans la mémoire de chaque processus. Cette connaissance doit être distribuée : l’ensemble des informations partielles relatives à l’arbre stockées dans la mémoire de chaque processus doit permettre de reconstituer entièrement cet arbre. De plus, les informations locales doivent être utiles. Dans notre contexte, elles doivent permettre de router une information d’un processus quelconque jusqu’au puits. Ainsi, on a simplement besoin, pour chaque processus non puits, d’une variable pointeur, communément appelé pointeur « parent », qui pointera le numéro de port de son lien appartenant au chemin élémentaire de l’arbre le reliant au puits. Par exemple, le pointeur parent de \(p_7\) dans la figure 4 devra avoir la valeur 0.

L’algorithme du « minimum plus un »

Nous proposons d’étudier maintenant un algorithme autostabilisant, connu sous le nom du « minimum plus un », permettant de calculer dans le modèle à passage de messages un arbre couvrant orienté vers le puits \(p_0\). L’arbre calculé par l’algorithme aura une propriété supplémentaire intéressante : pour chaque processus \(p_i\), la longueur (en nombre de sauts) de l’unique chemin élémentaire dans l’arbre le reliant au puits \(p_0\) sera égale à la distance entre \(p_i\) et \(p_0\). Dans un réseau bidirectionnel connexe, la distance entre deux processus \(p\) et \(q\) est égale à la longueur du plus court chemin reliant \(p\) et \(q\). L’exemple donné dans la figure ci-dessous a cette propriété : par exemple, le chemin de l’arbre reliant \(p_6\) à \(p_0\) est bien de longueur minimum, 3, c’est-à-dire qu’il contient trois arêtes.

L’algorithme est très simple. Chaque processus \(p_i\) va calculer sa distance au puits dans une variable de type entier naturel, notée \(p_i.d\). Pour corriger les éventuelles pannes transitoires, \(p_0\) devra simplement affecter régulièrement \(p_0.d\) à 0 (\(p_0\) est à distance zéro de lui-même !). Ensuite, les autres processus ont besoin de connaître la distance calculée par leurs voisins pour évaluer la leur. Pour ce faire, chaque processus (y compris le puits) envoie régulièrement un message contenant la valeur de sa variable distance (un entier positif ou nul initialement quelconque) dans chacun de ses liens de communication. Lorsqu’un processus \(p_i\) reçoit un tel message, il stocke cette information dans un tableau où chaque case est associée à un des numéros de port incidents à \(p_i\). Ainsi, la case \(j\) du tableau du processus \(p_i\) contiendra la dernière valeur de distance qu’il aura reçue depuis son port \(j\). Après avoir stocké l’information reçue, \(p_i\) effectue les tâches suivantes s’il n’est pas le puits :

1. il réévalue \(p_i.d\) pour qu’elle soit égale à la valeur minimale de son tableau plus un et ensuite ;
2. il désigne avec son pointeur parent le numéro de port associé à la valeur minimale de son tableau. (S’il existe plusieurs minima, on discriminera en choisissant le numéro de port le plus petit parmi les candidats.)

Un exemple d’exécution de l’algorithme est visible dans la vidéo ci-dessous :

Pourquoi ça stabilise ?

Pour démontrer l’autostabilisation du système, on peut tout d’abord remarquer que \(p_0.d\) va prendre pour valeur constante zéro et à partir de ce moment là envoyer uniquement des messages contenant la valeur de distance 0. De la même manière, les processus non-puits \(p_i\) finissent par satisfaire pour toujours \(p_i.d > 0\) et ainsi envoyer uniquement des messages contenant des valeurs strictement positives. Ainsi les voisins de la racine finissent par recevoir uniquement des messages avec la valeur 0 venant de la racine et uniquement des messages contenant des valeurs strictement positives de la part de leurs autres voisins. Par conséquent, ils fixent pour toujours leur variable distance à 1 et leur pointeur parent au numéro du lien les reliant à \(p_0\). Les autres processus (à distance au moins deux de \(p_0\)) finissent par recevoir uniquement des messages contenant des valeurs strictement positives et ainsi leurs variables distances finissent par devenir pour toujours strictement supérieures à 1. En continuant ce raisonnement en faisant augmenter peu à peu la distance, chaque processus va finir par assigner sa variable distance à la distance réelle qui le sépare du puits et fixer son pointeur parent pour désigner le lien de communication vers le premier processus d’un plus court chemin entre lui et le puits : on obtient finalement un arbre couvrant enraciné en \(p_0\). Un exemple d’état légitime de l’algorithme est donné dans la figure 5 ci-dessous.

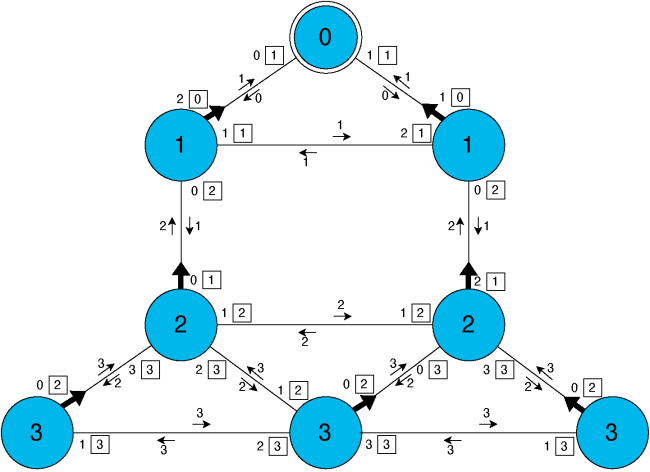
Figure 5 : Exemple d’état légitime de l’algorithme autostabilisant de calcul d’arbre couvrant. Les flèches épaisses représentent les pointeurs parent. Pour chaque processus \(p_i\), chaque couple \(j\boxed{k}\) » représente son numéro de port \(j\) et la valeur de distance \(k\) associée. Les flèches fines et leurs valeurs associées représentent des messages en transit.

On peut remarquer que notre algorithme est insensible à l’ordre de réception des messages : cet ordre n’intervient pas dans la preuve de stabilisation. Cette propriété rend l’algorithme plus général puisque, par exemple, dans les réseaux superposés (en anglais overlay networks) les liens de communication ne sont pas nécessairement FIFO (NB : Un lien de communication est FIFO si l’ordre de réception des messages par ce lien suit l’ordre d’émission. En effet, FIFO, c’est-à-dire First In, First Out, signifie premier entré, premier sorti.). Enfin, si le système subit des pertes de messages fréquentes, donc non transitoires (on parlera alors de pannes intermittentes au lieu de transitoires), la convergence reste effective si ces pertes de messages sont équitables, ce qui signifie que dans tout lien de communication, si une infinité de messages est envoyée alors une infinité de messages est reçue. Par exemple, un lien où un message sur deux est perdu vérifie cette hypothèse.

Conclusion

De nombreuses recherches fructueuses ont été conduites autour de l’autostabilisation depuis son introduction en 1974. Ces recherches ont mené à des solutions toujours plus efficaces en termes de coût (mémoire et temps, en particulier temps de stabilisation) ou encore en termes de qualité de service. Les développements récents en autostabilisation permettent d’envisager des applications concrètes dans des systèmes où l’intervention humaine en cas de défaillances est impossible ou tout du moins non souhaitable. Ces systèmes incluent, entre autres, les réseaux informatiques à grande échelle (typiquement Internet), les satellites ou encore les réseaux de capteurs sans fil. Par exemple, les réseaux de capteurs sans fil sont des réseaux composés d’une multitude de petits dispositifs, appelés capteurs, pourvus d’instruments capables de mesurer des données physiques (température, pression, …) sur l’environnement qui les entoure et de les échanger par transmission radio. Ces réseaux sont souvent déployés dans des milieux hostiles sans infrastructure préexistante comme le long d’un volcan ou dans une forêt dense. Une application typique dans ces réseaux est la remontée de données en un capteur puits, qui fait office de passerelle vers un autre réseau comme Internet. Une telle application peut être mise en place à l’aide d’un algorithme autostabilisant de calcul d’arbre couvrant et ainsi bénéficier des propriétés de tolérance aux pannes intrinsèques d’un tel algorithme.