
Modéliser la COVID-19 : de la population à l’individu
Rappel du contexte
Un nouveau virus, une crise sanitaire mondiale

Un nouveau coronavirus, le SARS-CoV 2 (Severe Acute Respiratory Syndrome – related CoronaVirus 2), est apparu en Chine dans la province du Hubei en décembre 2019. À l’origine d’une infection respiratoire à transmission interhumaine particulièrement contagieuse appelée COVID-19, il s’est propagé dans le monde en quelques semaines provoquant
dans son sillage une crise sanitaire mondiale.
Il est rapidement constaté que cette nouvelle maladie, transmise par voie respiratoire, peut être à l’origine d’infections pulmonaires sévères nécessitant une hospitalisation et une supplémentation en oxygène, en particulier chez les personnes âgées ou présentant une maladie chronique. En l’absence de traitement efficace et alors que les pays touchés font face à une vague d’hospitalisations et de décès, des mesures de contrôle de l’épidémie sont mises en œuvre par de nombreux gouvernements à travers le monde. Ces mesures, regroupant à la fois des consignes d’hygiène individuelles comme le port du masque et le lavage des mains, et des mesures collectives de distanciation sociale comme la fermeture des écoles, la restriction des déplacements ou le confinement, ont pour objectif de réduire la transmission du virus entre les individus et ainsi ralentir la propagation de l’épidémie.
Alors que la recherche d’un traitement curatif efficace se révèle tortueuse, le développement vaccinal progresse de manière exceptionnelle. Un an seulement après la découverte du SARS-CoV 2, plusieurs vaccins efficaces contre la maladie, en particulier contre ses formes graves, sont commercialisés. La course à la production massive et à la vaccination du plus grand nombre a démarré. Elle continue désormais, plus de trois ans après la découverte du SARS-CoV 2, du fait de l’apparition de variants du virus qui continuent à nourrir le besoin de nouvelles stratégies de protection.
Modèles mathématiques à compartiments : l’exemple du modèle SEIRAH
Le SARS-CoV 2 est un nouvel agent infectieux, la quasi-totalité des individus de la population mondiale ne possède préalablement aucune protection immunitaire contre cette infection (bien que des protections croisées avec d’autres coronavirus puissent exister), l’ensemble de la population y est donc sensible : on parle de population susceptible. En l’absence de mise en œuvre de mesures de contrôle ou de freinage et en l’absence de réinfection, l’épidémie évoluerait sous la forme d’une vague unique, et ce indépendamment du modèle mathématique choisi pour la modéliser : une augmentation croissante du nombre quotidien de nouvelles infections jusqu’à atteindre un pic, puis une décroissance progressive. Au fur et à mesure qu’une part croissante de la population est infectée et développe une immunité protectrice, la part de la population susceptible décroît jusqu’à ce que l’épidémie disparaisse naturellement. Malgré le nombre important d’hypothèses qu’ils génèrent, les modèles mathématiques compartimentaux SIR sont particulièrement adaptés à la modélisation de cette dynamique, en catégorisant la population en compartiments susceptibles (\(S\)), infectés (\(I\)) et retirés (\(R\), guéris ou décédés). Ce type de modèle a été décrit extensivement dans un article Interstices précédent.
L’équipe de recherche SISTM (Statistics In System biology and Translational Medicine) s’est intéressée à cette question à l’aide d’un modèle à compartiments basé sur SIR. Ajouter le compartiment E pour « Exposés » est classique afin de prendre en compte la période d’incubation. L’idée est ensuite d’ajouter un compartiment H pour « Hospitalisés » afin de pouvoir estimer le modèle à partir des données d’hospitalisations extrêmement fiables en France (base de données SI-VIC). Le fait d’introduire un compartiment (A) de personnes infectées asymptomatiques, c’est-à-dire qui ne présentent pas de symptômes, ou paucisymptomatiques (avec peu de symptômes), permet de mieux modéliser les politiques de tests en début de crise, qui n’ont été effectués qu’après l’apparition des symptômes. La création de ces nouveaux compartiments permet de définir le modèle SEIRAH qui se retranscrit en un système d’équations différentielles faisant apparaître des paramètres de dynamique. La définition mathématique du modèle SEIRAH est donnée sur la figure 1 ci-dessous et la Table 1 décrit les paramètres.
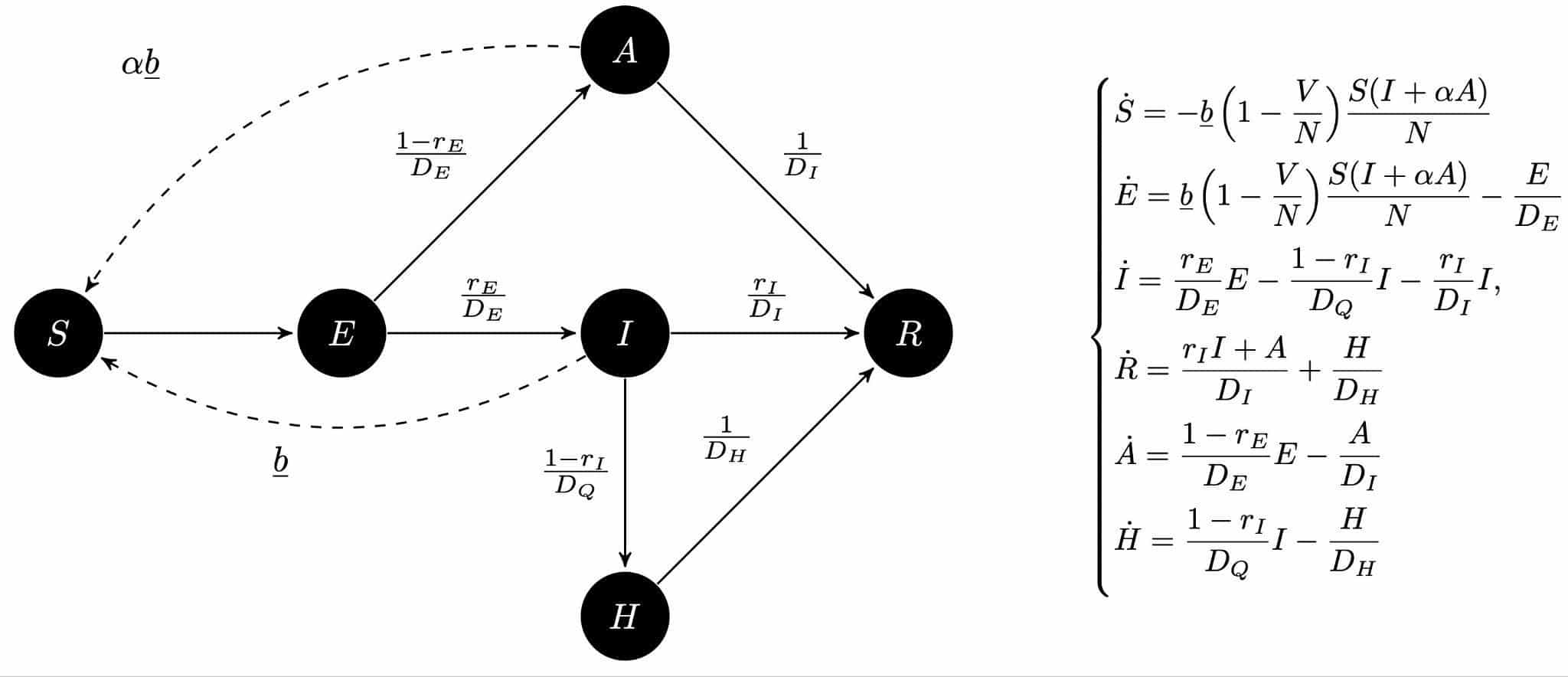
Figure 1. Modèle SEIRAH. \(S\) représente la population susceptible, \(E\) la population en phase d’incubation, \(I\) la population infectée non hospitalisée, \(H\) la population hospitalisée, \(A\) la population infectée non confirmée (typiquement les asymptomatiques) et \(R\) la population retirée : guérie ou décédée. Enfin, \(V\) représente le nombre de personnes vaccinées dans la population. Ce modèle en l’état fait donc l’hypothèse que toute personne vaccinée est immunisée avec une efficacité contre la transmission du virus de 100% de manière permanente. Les flèches représentent les transferts possibles entre les compartiments. Chaque flèche est annotée par des taux de transfert dont la description se trouve dans la Table 1 ci-après.
| Paramètres | Interprétation | Valeur |
| \(\underline{b}\) | Taux de transmission des cas infectieux | Estimé par région |
| \(r_E\) | Taux de confirmation | 0,84 |
| \(r_I\) | Taux de non-hospitalisation | 0.97 |
| \(\alpha\) | Coefficient de réduction de transmission chez les asymptomatiques | 0,55 |
| \(D_E\) | Période d’incubation | 5,1 jours |
| \(D_I\) | Période d’infectiosité | 5 jours |
| \(D_Q\) | Durée entre l’apparition des symptômes et l’hospitalisation | 5,9 jours |
| \(D_H\) | Durée d’hospitalisation | 18,3 jours |
| \(N\) | Taille de la population | Nombre d’habitants par région |
Table 1. Paramètres du modèle SEIRAH avec leurs interprétations. |
||
Diverses mesures de contrôle de l’épidémie ont été mises en place et il fut nécessaire d’évaluer leur efficacité en faisant l’hypothèse que celles-ci jouaient sur la transmission. À l’aide du modèle SEIRAH, cela fut possible en imposant une dynamique temporelle au taux de transmission. Avant le confinement du 17 mars 2020, la transmission a une valeur différente pour chaque région \(i\). Cette variabilité inter-régions est statistiquement contrainte dans la population en supposant que chaque région \(i\) a une transmission qui dévie d’une quantité \(u_i\) de la transmission moyenne d’une manière normalement distribuée entre toutes les régions avec une variance \(\sigma_{\beta}\), ce que l’on note en abrégé \(u_i \sim {\mathcal{N}} (0, \sigma_{\beta})\). Après le 17 mars 2020, la transmission initiale \(\underline{b}_0\) est divisée pour toutes les régions par \(\exp(\beta)\). On pose alors le modèle à effets mixtes suivant :
- \(\log(\underline{b}_i(t)) = \log(\underline{b}_0 ) + u_i\), avant le 17 mars 2020
- \(\log(\underline{b}_i(t)) = \log(\underline{b}_0) – \beta + u_i\), après le 17 mars 2020,
où \(u_i \sim {\mathcal{N}} (0, \sigma_{\beta}), \beta > 0.\)
Ce modèle peut être facilement étendu pour un plus grand nombre d’interventions de santé publique. À noter, l’utilisation de la transformation \(log\) pour le paramètre de transmission dans le modèle permet aux modélisateurs d’assurer la positivité des taux de transition estimés pour le modèle SEIRAH.
Des modèles aux données : quels enjeux de recherche ?
Pour finir, il est essentiel de relier notre modèle aux données en intégrant un modèle d’observation qui prend en compte l’erreur de mesure sous la forme d’une incertitude aléatoire pouvant être faite dans le report des données. Nous notons \(\theta\) l’ensemble des paramètres du modèle. Dans la formule, par exemple, pour une série de données d’hospitalisations prévalentes pour la région \(i\) au jième temps d’observation noté \(t_{ij}\), où \(H\) représente la solution du système d’équation différentielle SEIRAH pour le compartiment \(H\) auquel s’ajoute un terme d’erreur de mesure dont la magnitude est estimée par le paramètre \(\sigma\), nous avons :
Un premier enjeu de recherche réside dans la modélisation : trouver un modèle suffisamment simple qui capture la dynamique des phénomènes observés. Pour cela, il faut étudier l’ « identifiabilité » du modèle et de ses paramètres. C’est-à-dire qu’il doit être possible de déduire de manière unique la valeur des paramètres à partir des sources de données disponibles. Le cas échéant, certains paramètres, comme c’est le cas ici, doivent être fixés à des valeurs prises dans la littérature.
Un second enjeu est l’ajustement ou estimation du modèle, qui consiste à faire en sorte que celui-ci reproduise effectivement ce qui a été observé dans le passé. Il s’agit d’une étape essentielle avant toute extrapolation des résultats. Il est nécessaire de développer des méthodes d’ajustement du modèle aux données : s’opposent alors les méthodes de calibration et les méthodes d’estimation. La calibration explore sur une grille quelles valeurs de paramètres permettent de mieux reproduire les trajectoires observées. L’estimation permet quant à elle de résoudre un problème inverse, c’est-à-dire de retrouver à partir des données les valeurs des paramètres du modèle qui permettent de minimiser l’écart entre les données observées et les résultats du modèle, à l’aide d’une fonction appelée la vraisemblance. Le développement de nouvelles méthodes d’estimation fait aussi l’objet de nos recherches.
Enfin, il existe un enjeu sur l’évaluation des qualités de prédiction du modèle. Il est nécessaire de garder en tête l’objectif d’usage de ces modèles et de bien distinguer qu’avoir une bonne qualité d’ajustement aux données n’assure pas nécessairement une bonne qualité de prédiction. Ces approches de choix de modèles sont au cœur de la recherche sur les modèles compartimentaux.
Afin de générer des résultats épidémiologiques solides, ces méthodes statistiques sont complexes, lourdes en termes de temps de calcul et nécessitent des centres de calcul parallèles dédiés.
Vague épidémique : et si nous avions laissé faire ?
Avec le modèle SEIRAH précédemment décrit, il a été estimé sur la première vague qu’en l’absence d’intervention, plus de 90 % de la population française aurait été infectée à la fin de l’épidémie, avec un pic atteignant près de 900 000 hospitalisations simultanées (voir la référence bibliographique 2). À titre de comparaison, environ 380 000 lits d’hospitalisation (publics et privés confondus) ont été recensés en France. Des travaux similaires, menés en Grande-Bretagne et aux USA, ont également estimé que plus de 80 % de la population aurait été infectée en l’absence de mesures de contrôle, provoquant un pic d’hospitalisation en soins intensifs dépassant de 30 fois les capacités de soin (voir la référence bibliographique 3).
Dans l’urgence de l’épidémie, comprendre la dynamique épidémique et évaluer l’impact des mesures de contrôle
Toujours avec le modèle SEIRAH, les premiers travaux de modélisation de la COVID-19 ont eu pour objectif d’estimer rétrospectivement les paramètres de la dynamique épidémique, comme le nombre de reproduction de base (voir l’article Des modèles numériques pour aider à contrôler une épidémie), le taux d’hospitalisation ou le taux de mortalité (voir les références bibliographiques 2, 4, 5). Prenons l’exemple du nombre de reproduction de base, aussi appelé \(R_0\). Tout d’abord, rappelons que le nombre de reproduction de base correspond au nombre moyen d’individus contaminés par une personne infectée placée dans une population susceptible. Cet indicateur est intrinsèque à un pathogène. Ce nombre reflète le niveau de contagiosité de l’infection et constitue un des paramètres clés de la dynamique épidémique. Plus le \(R_0\) est élevé, plus l’agent infectieux se propage rapidement dans la population et plus la proportion de la population finalement infectée à la fin de la vague épidémique est importante (voir Figure 2). À l’inverse, s’il est au-dessous de 1, l’épidémie s’éteint. Dès lors que des politiques de santé publique sont mises en place, on ne parle plus de \(R_0\) mais de nombre de reproduction effectif (\(R_e\)). Ces deux indicateurs ont la même formule mathématique. Pour les estimer, nous avons besoin de données de vie réelle afin d’ajuster notre modèle. Dans le cas du modèle SEIRAH, ces indicateurs se calculent à l’aide de la méthode dite de matrice de nouvelle génération (voir la référence bibliographique 16) qui s’intéresse aux valeurs propres du système d’équations différentielles :
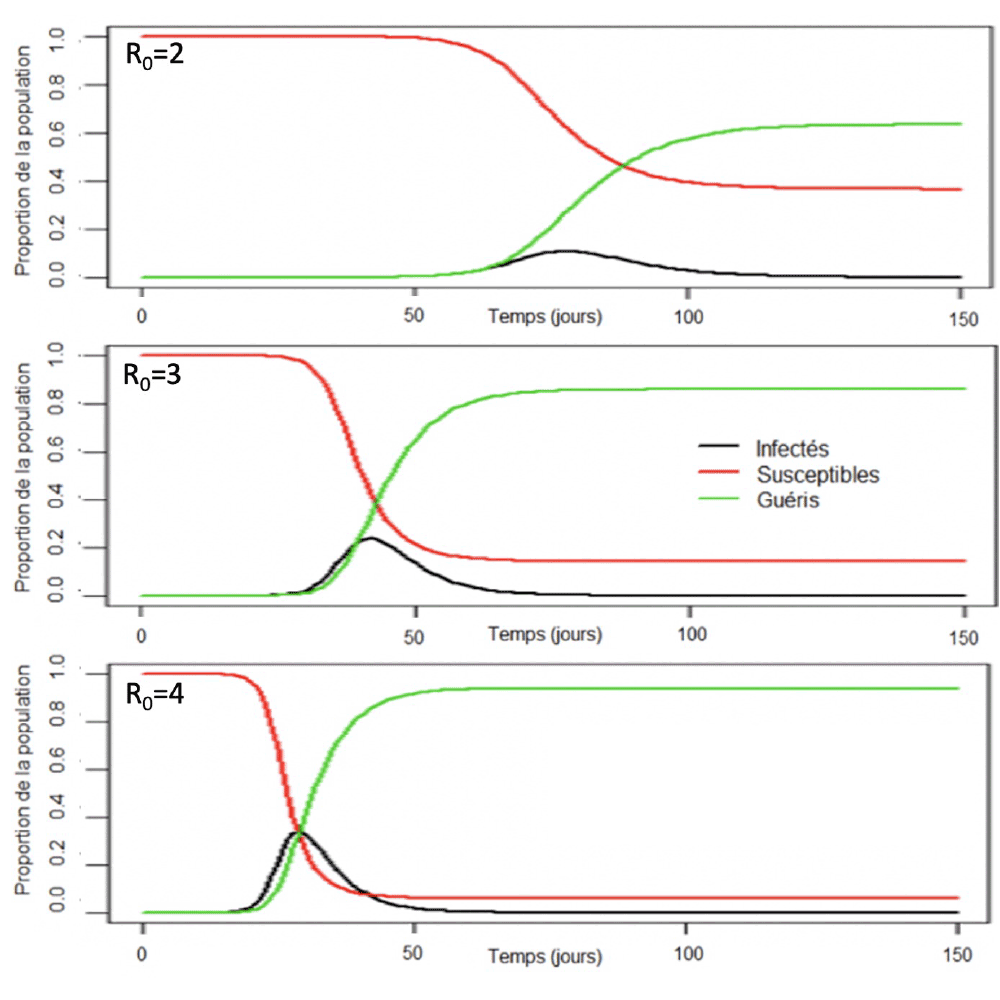
Figure 2. Proportions de la population susceptible, infectée ou retirée au cours du temps modélisées par un modèle SEIRAH pour différentes valeurs de \(R_0\) (2, 3 ou 4).
Avec le modèle SEIRAH, nous trouvons ainsi qu’en France le \(R_0\) au début de l’épidémie de SARS-CoV-2 est de 3,1, avec un intervalle de confiance à 95 % entre 2,95 et 3,26 une fois l’impact de la météo pris en compte. Ce résultat est corroboré par d’autres équipes de recherche françaises qui ont estimé, dès le début de l’épidémie, que le \(R_0\) se situait entre 2,81 et 3,3 en France (voir les références bibliographiques 2, 4, 5). D’autres travaux, menés dans différentes zones géographiques, ont confirmé que le \(R_0\) du SARS-CoV 2 se situait aux alentours de 3. Ces estimations peuvent varier d’une région géographique à l’autre du fait d’hétérogénéités dans les structures de contacts, de variations des conditions météorologiques qui influencent la transmission, ou du fait de la présence ou non de mesures de freinage.
Devant la progression de l’épidémie, différentes mesures de contrôle, inspirées de la gestion des pandémies grippales, ont été mises en place en urgence dans le monde. En France, la première vague épidémique a été contrôlée par la mise en place d’un confinement strict (décrit plus haut). À l’issue de ce confinement, différentes stratégies de relâchement des mesures ont été modélisées afin de guider au mieux les décisions de santé publique. Par exemple, ces travaux menés avec le modèle SEIRAH mais aussi d’autres approches étudiées par d’autres équipes ont montré qu’une faible proportion de la population avait été infectée à la sortie de la première vague, suggérant qu’une reprise épidémique importante surviendrait en cas de relâchement complet des restrictions (voir les références bibliographiques 2, 6). D’autres travaux ont exploré différentes stratégies de réouverture des écoles (voir la référence bibliographique 7) ou de priorisation vaccinale (voir la référence bibliographique 8). Il est important de comprendre que ces travaux n’ont pas pour objectif de prédire le futur mais plutôt de dégager des tendances évolutives en fonction de différents scénarios préalablement établis. En effet, ces prévisions dépendent directement d’hypothèses difficilement prévisibles, comme le niveau d’adhésion à la vaccination ou le comportement des populations.
D’autres travaux de modélisation ont eu pour objectif de prédire de manière précise l’évolution à très court terme du nombre d’hospitalisations afin de pouvoir par exemple anticiper la planification des activités hospitalières. Dans le cadre de la COVID-19, ces travaux ont été menés à l’échelle nationale (voir la référence bibliographique 9) et locale (voir la référence bibliographique 10). Néanmoins, le meilleur modèle prédictif à un instant peut rapidement être dépassé du fait du caractère très évolutif de l’épidémie de COVID-19. L’apparition imprévisible de nouveaux variants, la modification des stratégies vaccinales ou encore les changements de comportement des populations constituent autant d’obstacles à la génération de prédictions fiables.
Nos travaux ont estimé que le nombre de reproduction effectif \(R_e\) a été réduit d’environ 78 % (avec un intervalle de confiance entre 74 % et 82 %) au cours du premier confinement. Ces résultats sont corroborés par d’autres études (voir la référence bibliographique 4) et confirmés par des données de mobilité (voir la référence bibliographique 6). Néanmoins cette estimation globale ne permet pas de juger de l’efficacité de chacune des mesures prises au cours de cette période, que cela soit la fermeture des écoles, le télétravail, le port du masque ou la restriction des déplacements.
Vers une meilleure stratégie de contrôle ?
Il est particulièrement difficile d’établir un lien causal entre l’application d’une mesure et le contrôle de l’épidémie, puisqu’il n’est pas possible de comparer deux populations aux caractéristiques identiques dont une serait exposée à la mesure de contrôle et l’autre non. Grâce au modèle SEIRAH, l’équipe de recherche SISTM a cependant évalué l’association entre l’implémentation de mesures de santé publique et l’évolution de la transmission. Dans ce travail (voir la référence bibliographique 11), la fermeture isolée des écoles ou des bars et des restaurants étaient à l’origine d’une réduction modérée du taux de transmission de 7 et 10 % respectivement, alors que l’application des gestes barrières induisait une baisse de 46 %. Le couvre-feu réduisait la transmission d’environ 30 % quelle que soit l’heure de survenue (18 ou 20 heures). De manière intéressante, ce travail a retrouvé un effet significatif des conditions météorologiques avec une transmission augmentée d’environ 10 % en hiver et diminuée de 20 % en été.
Une fois l’effet de chaque mesure connu, il est possible d’essayer de prédire quelle est la meilleure stratégie de contrôle pour répondre à une future reprise épidémique. La meilleure stratégie de contrôle n’est pas seulement celle qui réduit la transmission virale, mais peut aussi être celle qui réduit au maximum le nombre de décès avec un moindre coût socio-économique. Au sein de l’équipe SISTM, nous avons donc impulsé la création de l’outil EpidemiOptim ayant pour objectif de proposer des stratégies optimales d’allocation d’interventions. La méthode intègre une approche d’apprentissage par renforcement sur des modèles épidémiques (voir la référence bibliographique 12) dans laquelle il s’agit de minimiser une fonction de coût en explorant les différentes stratégies possibles de manière parcimonieuse. Cet outil, qui requiert néanmoins une bonne connaissance du langage de programmation Python, a l’avantage de pouvoir s’adapter à différents publics, qu’ils soient statisticiens (modification des algorithmes d’apprentissage), épidémiologistes (modification des modèles à compartiments), économistes voire décideurs (modification des fonctions de coût) en proposant une interface facilitant leur collaboration.
Et dans le futur ?
Alors que l’épidémie dure depuis plus de 3 ans maintenant et que la campagne vaccinale a permis de protéger une large partie de la population française, nous avons progressivement abandonné toutes les règles de distanciation sociale et les gestes barrières. En effet, la majorité de la population a déjà été vaccinée ou infectée, et a donc développé une immunité. Néanmoins, on observe que cette immunité n’est pas définitive et s’estompe au fil du temps ou avec l’apparition de variants, ce qui fait s’éloigner la perspective de la fin de l’épidémie. Pour modéliser la perte de l’immunité, on peut utiliser un modèle SIR-étendu-S / SEIRAH-étendu-S dans lequel les individus retirés et protégés regagnent au bout d’un certain temps le compartiment des individus susceptibles (\(R \Rightarrow S\)). Nous avons vu précédemment, avec un modèle SIR simple, qu’en l’absence d’intervention l’épidémie évoluerait sous la forme d’une vague unique d’infections. Néanmoins, en cas de perte progressive de l’immunité, cette première vague serait systématiquement suivie quelles que soient les stratégies de contrôle d’une reprise épidémique à un intervalle d’autant plus rapproché que l’immunité s’estompe vite.
Il est possible de complexifier encore ce modèle en ajoutant un compartiment pour les individus vaccinés qui pourront perdre leur immunité vaccinale au cours du temps (\(V \Rightarrow S\)). C’est ce qui a été réalisé dans une étude ayant pour objectif d’évaluer la possibilité de relâcher toutes les mesures de contrôle en France, en particulier les gestes barrières (port du masque, lavage des mains etc.), en tenant compte de la vaccination et de la perte de l’immunité au cours du temps (voir la référence bibliographique 13). Dans ce travail, l’équipe SISTM, à l’aide d’un modèle SEIRAH-étendu prenant en compte la vaccination, l’âge de la population et la sévérité des symptômes liés à l’infection, a montré que seule une vaccination large de tous les enfants et adultes éligibles permettrait un relâchement complet des gestes barrières sans dépasser les capacités du système de santé. Ce travail souligne également l’importance de prendre en compte la perte d’immunité dans la modélisation de l’épidémie, afin de ne pas sous-estimer l’ampleur d’une éventuelle recrudescence épidémique. Mais une question centrale persiste, quelle est la durée de cette immunité ?
Vers les modèles intra-hôtes
Comme nous l’avons vu, les modèles mathématiques à compartiments ont été largement utilisés pour appréhender la dynamique de l’épidémie de COVID-19 à l’échelle d’une population (aussi appelée modélisation inter-hôte, c’est-à-dire entre les individus). Ces mêmes outils mathématiques peuvent être utilisés pour modéliser, à l’échelle de l’individu, les mécanismes régissant la dynamique entre la réplication virale et la réponse immunitaire (aussi appelée modélisation intra-hôte, i.e. à l’intérieur d’un individu). Au lieu de modéliser des flux d’individus susceptibles et infectés à l’échelle d’une population, il est possible de s’intéresser aux cellules non infectées, aux cellules infectées et à la charge virale à l’intérieur du corps humain. C’est à l’aide de ce type de modèle, en couplant les données immunologiques et virales in vivo aux données de réponse clinique, qu’il est par exemple possible d’estimer la durée de l’immunité. Plus largement, dans l’équipe SISTM nous avons montré que les modèles à compartiments peuvent permettre de définir des corrélats de protection (voir la référence bibliographique 14). Ce sont des biomarqueurs qui permettent de prédire l’immunité d’un individu (par exemple un niveau de fonction neutralisante pour les anticorps, aussi appelés ED50). Les corrélats de protection pourraient permettre de déduire, à partir du dosage d’un biomarqueur, le niveau de protection contre l’infection. Ils peuvent donc s’avérer particulièrement utiles dans le contrôle des épidémies, en particulier dans un monde où les infections, les hospitalisations et les décès devraient devenir de moins en moins fréquents.
Conclusion
L’épidémie de COVID-19 a constitué un formidable terrain d’application pour les modèles mathématiques à compartiments. Néanmoins, comme nous l’avons déjà abordé, ces modèles ont des limites qu’il convient de connaître. En effet, ils permettent de ne modéliser qu’un processus moyen au sein d’une population homogène. Ils ne prennent par exemple pas en compte les réseaux de contacts plus ou moins denses qui existent dans nos populations. De plus, ils ne tiennent pas compte de la dimension aléatoire de la dynamique épidémique (c’est-à-dire de la stochasticité). Ils constituent cependant un outil d’aide précieux à la gestion de la crise en urgence. À mesure que l’épidémie avance ou que d’autres épidémies apparaîtront, ces modèles sont amenés à évoluer et à s’intéresser de plus en plus à la dynamique intra-hôte (voir la référence bibliographique 15). Les avancées méthodologiques et les nouveaux challenges amenés par les épidémies permettront un jour de construire des modèles épidémiques globaux permettant d’agréger conjointement des données multi-échelles à l’échelle des individus et de la population.
- François Rechenmann. Modéliser La Propagation d’une Épidémie. Interstices. November 28, 2011. hal-00793043
- Prague, M.; Wittkop, L.; Collin, A.; Dutartre, D.; Clairon, Q.; Moireau, P.; Thiébaut, R.; Hejblum, B. P. Multi-Level Modeling of Early COVID-19 Epidemic Dynamics in French Regions and Estimation of the Lockdown Impact on Infection Rate; preprint; MedRxiv, 2020. https://doi.org/10.1101/2020.04.21.20073536
- Ferguson, N.; Laydon, D.; Nedjati Gilani, G.; Imai, N.; Ainslie, K.; Baguelin, M.; Bhatia, S.; Boonyasiri, A.; Cucunuba Perez, Z.; Cuomo-Dannenburg, G.; Dighe, A.; Dorigatti, I.; Fu, H.; Gaythorpe, K.; Green, W.; Hamlet, A.; Hinsley, W.; Okell, L.; Van Elsland, S.; Thompson, H.; Verity, R.; Volz, E.; Wang, H.; Wang, Y.; Walker, P.; Winskill, P.; Whittaker, C.; Donnelly, C.; Riley, S.; Ghani, A. Report 9: Impact of Non-Pharmaceutical Interventions (NPIs) to Reduce COVID19 Mortality and Healthcare Demand; Imperial College London, 2020. https://doi.org/10.25561/77482
- Salje, H.; Kiem, C. T.; Lefrancq, N.; Courtejoie, N.; Bosetti, P.; Paireau, J.; Andronico, A.; Hozé, N.; Richet, J.; Dubost, C.-L.; Strat, Y. L.; Lessler, J.; Levy-Bruhl, D.; Fontanet, A.; Opatowski, L.; Boelle, P.-Y.; Cauchemez, S. Estimating the Burden of SARS-CoV-2 in France. Science, 369(6500), 208-211. https://doi.org/10.1016/j.ijid.2021.08.029
- Roques, L.; Klein, E. K.; Papaïx, J.; Sar, A.; Soubeyrand, S. Using Early Data to Estimate the Actual Infection Fatality Ratio from COVID-19 in France. Biology 2020, 9 (5), 97. https://doi.org/10.3390/biology9050097
- Di Domenico, L.; Pullano, G.; Sabbatini, C. E.; Boëlle, P.-Y.; Colizza, V. Impact of Lockdown on COVID-19 Epidemic in Île-de-France and Possible Exit Strategies. BMC Med. 2020, 18 (1), 240. https://doi.org/10.1186/s12916-020-01698-4
- Di Domenico, L.; Pullano, G.; Sabbatini, C. E.; Boëlle, P.-Y.; Colizza, V. Modelling Safe Protocols for Reopening Schools during the COVID-19 Pandemic in France. Nat. Commun. 2021, 12 (1), 1073. https://doi.org/10.1038/s41467-021-21249-6
- Tran Kiem, C.; Massonnaud, C. R.; Levy-Bruhl, D.; Poletto, C.; Colizza, V.; Bosetti, P.; Fontanet, A.; Gabet, A.; Olié, V.; Zanetti, L.; Boëlle, P.-Y.; Crépey, P.; Cauchemez, S. A Modelling Study Investigating Short and Medium-Term Challenges for COVID-19 Vaccination: From Prioritisation to the Relaxation of Measures. EClinicalMedicine 2021, 38, 101001. https://doi.org/10.1016/j.eclinm.2021.101001
- Paireau, J.; Andronico, A.; Hozé, N.; Layan, M.; Crepey, P.; Roumagnac, A.; Lavielle, M.; Boëlle P.Y.; Cauchemez, S. (2022). An ensemble model based on early predictors to forecast COVID-19 health care demand in France. Proceedings of the National Academy of Sciences, 119(18), e2103302119. https://doi.org/10.1073/pnas.2103302119
- Ferté, T.; Jouhet, V.; Griffier, R.; Hejblum, B. P.; Thiébaut, R.; the Bordeaux University Hospital Covid-19 crisis task force. The benefit of augmenting open data with clinical data-warehouse EHR for forecasting SARS-CoV-2 hospitalizations in Bordeaux area, France. JAMIA Open, 2022, ooac086. https://doi.org/10.1093/jamiaopen/ooac086
- Collin, A.; Hejblum, B.P.; Vignals, C.; Lehot, L.; Thiébaut, R.; Moireau, P.; Prague, M.; Using Population Based Kalman Estimator to Model COVID-19 Epidemic in France: Estimating the Effects of Non-Pharmaceutical Interventions on the Dynamics of Epidemic. MedRXiV, 2021. https://doi.org/10.1101/2021.07.09.21260259
- Colas, C.; Hejblum, B.; Rouillon, S.; Thiébaut, R.; Oudeyer, P.-Y.; Moulin-Frier, C.; Prague, M. EpidemiOptim: A Toolbox for the Optimization of Control Policies in Epidemiological Models. J. Artif. Intell. Res. 2021, 71, 479–519. https://doi.org/10.1613/jair.1.12588
- Vignals, C.; Dick, D. W.; Thiébaut, R.; Wittkop, L.; Prague, M.; Heffernan, J. M. Barrier Gesture Relaxation during Vaccination Campaign in France: Modelling Impact of Waning Immunity. COVID 2021, 1 (2), 472–488. https://doi.org/10.3390/covid1020041
- Alexandre, M.; Marlin, R.; Prague, M.; Coléon, S.; …; Schwartz, O.; Sanders, R.; Le Grand, R.; Levy, Y.; Thiébaut, R. SARS-CoV-2 mechanistic correlates of protection: insight from modelling response to vaccines, BioRxiv, 2021. https://doi.org/10.1101/2021.10.29.466418
- Prague, M.; Alexandre, M.; Thiébaut, R.; Guedj, J. Within-host models of SARS-CoV-2: What can it teach us on the biological factors driving virus pathogenesis and transmission? Anaesth Crit Care Pain Med., 2022. https://doi.org/10.1016/j.accpm.2022.101055
- Diekmann, O.; Heesterbeek, J.A.P.; Roberts, M.G. The Construction of Next-Generation Matrices for Compartmental Epidemic Models. J. R. Soc. Interface, 2010. https://doi.org/10.1098/rsif.2009.0386
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Carole Vignals
Docteur au sein du service des maladies infectieuses et tropicales, au Centre Hospitalier Universitaire de Bordeaux.

Boris Hejblum
Chargé de recherche Inserm, en Biostatistique, dans l'équipe de recherche SISTM commune à Bordeaux Population Health (Inserm U1219) et au centre Inria de l'Université de Bordeaux.

Mélanie Prague
Chargée de recherche Inria dans l'équipe de recherche SISTM commune à Bordeaux Population Health (Inserm U1219) et au centre Inria de l'Université de Bordeaux.
