
Peut-on quantifier l’importance du périphérique parisien ?
On se propose d’étudier le cas de la ville de Paris avec un plan autoroutier imaginé dans les années 1960 et soutenu par le président de la République de l’époque, Georges Pompidou. Nous allons étudier l’impact qu’aurait eu ce plan s’il avait été suivi en identifiant les trajets en voiture qui auraient capté le plus de trafic en raison de la structure même de ce réseau autoroutier urbain. Pour cela nous allons quantifier, moyennant quelques hypothèses, la fréquence avec laquelle les usagers parisiens auraient parcouru chaque tronçon d’autoroute.
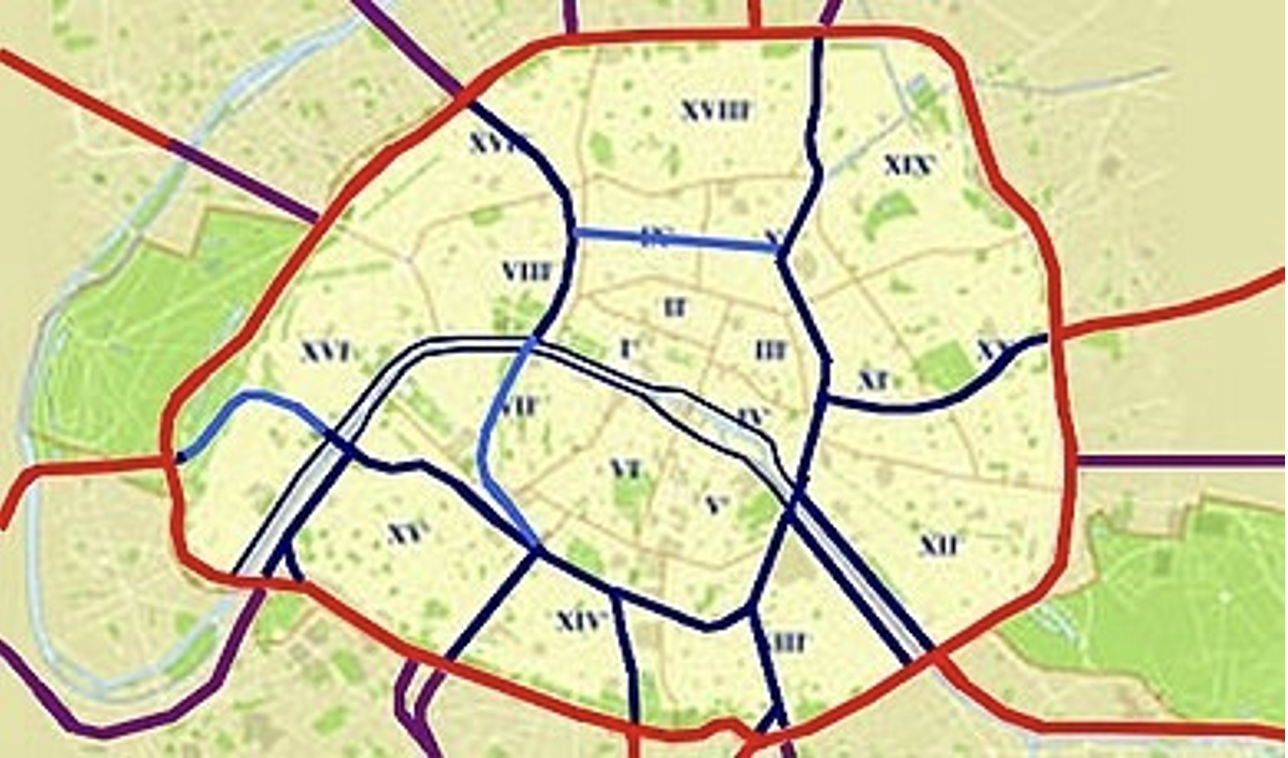
Figure 1 : Le plan autoroutier imaginé pour Paris (en rouge les axes déjà existants, en violet les axes prévus, en bleu les axes intra-muros prévus et en bleu-clair les axes enterrés prévus).
Un modèle simplifié
Avant d’utiliser une théorie, il convient d’en définir ses personnages principaux. Un graphe modélise des interactions entre différents acteurs. Mathématiquement, les acteurs sont des points appelés sommets et les interactions sont des liens entre les sommets appelés arêtes. Un graphe est donc une structure composée de sommets reliés, pour certains d’entre eux, par des arêtes. Dans notre cas de rocade, les arêtes sont clairement les axes autoroutiers (à double sens de circulation). Les sommets seront les lieux de sorties (et d’entrées) de la rocade. Ainsi, un graphe simpliste d’une situation urbaine de rocade serait le graphe suivant.
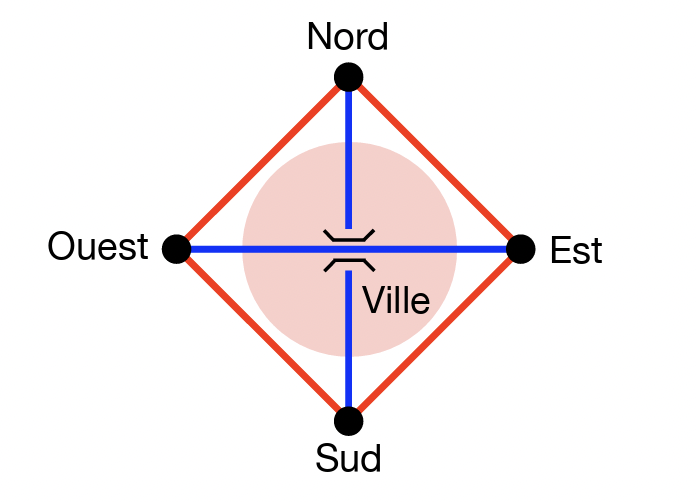
Figure 2 : Un modèle simplifié.
Les arêtes rouges forment une rocade à 4 sorties situées à chacun des 4 points cardinaux. Les arêtes bleues sont les autoroutes qui traversent la ville (suivant l’urbanisme à la Pompidou !) et relie l’agglomération à la rocade. Nous avons ajouté un pont pour que les autoroutes se croisent sans carambolages. Notez que, dans ce premier modèle simplifié, il n’est pas possible de passer d’une autoroute à l’autre au niveau du pont, et que la ville elle-même n’est pas un sommet du graphe. En effet, ce n’est ni une entrée, ni une sortie d’autoroute ou de la rocade.
Nous allons maintenant essayer de mesurer l’importance effective des routes de la ville à l’aide d’une voiture. Imaginons donc une voiture parcourant ces routes au hasard pendant un très long trajet, disons pendant au moins un million d’arêtes. Plus précisément, la voiture démarre du sommet de son choix et avance dans le graphe arête après arête. Quand elle est sur un sommet, elle choisit une nouvelle direction uniformément au hasard, ce que nous appelons en jargon mathématique une marche aléatoire. Dans notre exemple, la voiture aura toujours 3 directions possibles peu importe le sommet — on parle de graphe 3-régulier — et donc une chance sur trois de prendre une certaine direction. Quand le million d’arêtes parcourues est atteint, elle pourra continuer suivant les mêmes règles jusqu’à revenir à son point de départ (ce qui arrivera presque sûrement !) où elle s’arrêtera complètement, réalisant ainsi un chemin fermé sur le graphe. Une fois ce processus terminé, de notre côté, nous le relisons et prenons des notes : à chaque fois que la voiture fera un cycle (c’est-à-dire qu’elle repassera par un sommet déjà visité), nous mémoriserons ce cycle, nous l’effacerons de son trajet et nous laisserons la voiture continuer son chemin. Ce faisant, au bout de sa course, étant donné que la voiture revient à son point de départ, nous sommes censés noter un dernier cycle et, en l’effaçant, il n’y a plus de trajet. Nous avons donc conservé la liste des cycles parcourus par la voiture, parfois en un seul coup, parfois de manière éclatée. En effet, la voiture peut parcourir un bout d’un premier cycle, en faire entièrement un second, que l’on note et efface, et terminer le premier ensuite, que l’on note et efface également. Notez aussi que les cycles que nous retenons sont ce que l’on appelle des cycles simples au sens où, à l’intérieur d’eux-mêmes, il n’y a pas d’autres cycles.
Enfin, on calcule la fréquence d’apparition de chacun de ces cycles. Cela nous donne une notion d’importance qui semble correcte : même les cycles « éclatés » sont comptabilisés. Notons de plus que parmi les cycles dont on calcule ainsi la fréquence d’apparition, les plus courts, de longueur deux, sont les allers-retours sur les arêtes, et donc nous obtenons une quantification directe de l’importance de chaque lien entre sommets du graphe dans l’ensemble des trajets possibles sur celui-ci. En considérant aussi les cycles plus longs, de longueur trois ou plus, nous généralisons donc aux triangles, carrés, pentagones, etc., l’intuition selon laquelle une arête essentielle est souvent empruntée. On peut tout de suite deviner que, grâce aux symétries du graphe, les fréquences ne dépendent en fait que de la longueur du cycle (c’est-à-dire du nombre d’arêtes qui composent le cycle) : quelle différence y a-t-il significativement entre les cycles Nord – Ouest – Nord, Ouest – Nord – Ouest et Sud – Est – Sud ? Ou bien entre Nord – Est – Ouest – Nord et Sud – Est – Nord – Sud ? Aucune, ce sont des trajets très similaires !
Ainsi un ordinateur — parce que c’est plus rapide qu’une voiture — vous donnera les quantités suivantes : un cycle de longueur \(2\) a une importance de \(10,256 \%\) (c’est-à-dire que ce cycle est emprunté par \(10,256 \%\) de tous les trajets que la voiture peut faire sur ce réseau urbain) ; de longueur \(3\), \(3,846 \%\) ; de longueur \(4\), \(1,282 \%\). De plus, il y a \(6\) cycles de longueur \(2\), \(8\) de longueur \(3\) et \(6\) de longueur \(4\). Donc les allers-retours ont une importance relative de \(6 \times 10,256 \%\) \(=61,538\%\) ; les « triangles » ont une importance relative de \(30,769\%\) et les « carrés » ont une importance de \(7,693\%\). Autrement dit, les automobilistes ont beaucoup plus de chances de faire des allers-retours plutôt que le tour complet de la rocade. Rien de nouveau sous le soleil mais c’est normal : le modèle est très simplifié. Améliorons-le un peu !
À vous de jouer !
Pourquoi ne pas vous faire essayer ? Il y a cependant un souci : comment faire pour que vous nous donniez un graphe représentant votre situation de rocade ? En vérité, c’est très facile : on peut entièrement encoder un graphe par ce qu’on appelle sa matrice d’adjacence. Il s’agit d’un tableau à double entrée où, en ligne ainsi qu’en colonne, sont répertoriées les sommets du graphe (qu’on numérotera à partir de maintenant). Une cellule de ce tableau contient la valeur \(0\) si les sommets ne sont pas reliés, \(1\) s’ils le sont. Ainsi le graphe de la partie précédente se résume par le tableau suivant.
| 1 (Nord) | 2 (Ouest) | 3 (Sud) | 4 (Est) | |
| 1 (Nord) | 0 | 1 | 1 | 1 |
| 2 (Ouest) | 1 | 0 | 1 | 1 |
| 3 (Sud) | 1 | 1 | 0 | 1 |
| 4 (Est) | 1 | 1 | 1 | 0 |
La notation mathématique simplifie ce tableau en : \[ \left( \begin{array}{cccc} 0 & 1 & 1 & 1 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 \end{array} \right) \]
Nous avons un petit secret à vous partager : même si l’histoire de la voiture parcourant le graphe est correcte mathématiquement, nous avons une formule qui calcule exactement les fréquences. Si nous ne vous l’écrivons que maintenant c’est parce que cette formule repose sur la matrice d’adjacence du graphe ! Elle repose aussi sur une fonction mathématique mettant en jeu des matrices qu’on découvre en première année d’études supérieures scientifiques et qui porte très bien son nom : le déterminant. Elle fait aussi intervenir une quantité, provenant de la théorie des graphes, appelée valeur propre dominante : il s’agit, grosso modo, du nombre moyen de directions disponibles quand on se place sur un sommet du graphe (qui vaut clairement \(3\) dans le graphe de la partie « Un modèle simplifié »). Le déterminant et la valeur propre dominante d’une matrice d’adjacence sont faciles à obtenir pour un ordinateur, dans le sens où le nombre de calculs nécessaires à leur obtention ne grandit pas trop vite avec la taille du graphe. En effet si le graphe du réseau urbain comporte \(N\) sommets, l’ordinateur aura besoin d’environ \(N^3\) opérations élémentaires (additions et multiplications de nombres) pour les calculer. Pour un cycle donné ce coût computationnel de \(N\) cube reste très raisonnable, surtout si on le compare à d’autres questions célèbres de l’analyse des réseaux, comme le problème du voyageur de commerce.
Le test avec les vrais grands axes
Parlons de cette formule. Présentons-la d’abord sans artifice. La fréquence d’un cycle \(c\), notée \(f(c)\), est définie par la formule.\[ f(x) = \lambda ^{-\ell(c)} \det \left( I_{v(G \setminus c)} – \frac{1}{\lambda} A_{G \setminus c}\right) \]
Dans le sens de la lecture, \(\lambda\) est la valeur propre dominante qu’on a déjà rencontré plus haut. Elle est mise en puissance \(-\ell(c)\) où \(\ell(c)\) est la longueur du cycle \(c\). Ensuite, \(\det\) est la notation usuelle pour la fonction déterminant. Ce qui suit est donc une matrice ou, plutôt dans notre cas, une différence de deux matrices. La première est \(I_{v(G \setminus c)}\). Il s’agit d’une matrice dont les éléments diagonaux valent \(1\) et tous les autres \(0\) (on parle de matrice identité). Sa taille est le nombre de sommets du graphe \(G\) auquel on a retiré les sommets composant le cycle \(c\). La seconde matrice est \(A_{G \setminus c}\), il s’agit de la matrice d’adjacence du graphe \(G \setminus c\) c’est-à-dire du graphe \(G\) auquel on a retiré tous les sommets du cycle \(c\) et donc toutes les arêtes de ce cycle ainsi que les arêtes connectant le cycle au reste du graphe.
Maintenant que nous avons présenté les protagonistes de cette formule, il s’agit pour nous d’expliquer, en partie, sa provenance. Plus haut, nous avons introduit le calcul des fréquences par un (seul et long) trajet en voiture dont nous retenions progressivement chaque cycle (simple) parcouru avant de l’effacer et de continuer de suivre la trajectoire. En vérité, nous aurions pu observer plusieurs trajets (un peu moins longs) de plusieurs voitures et adopter la même procédure en mémorisant, cette fois et sur chaque trajet de chaque voiture, uniquement le dernier cycle. Les fréquences auraient été les mêmes sur les deux manières de présenter ! En effet, considérons un trajet de voiture dans lequel un certain cycle est parcouru mais n’est pas le dernier à être clos. En changeant le point de départ de ce trajet on peut créer un autre trajet empruntant exactement les mêmes arêtes et dans le même ordre relatif que le premier mais pour lequel le cycle qui nous intéresse est terminé en dernier. Ceci implique que la fréquence d’apparition de ce cycle dans un trajet est la même que sa fréquence d’apparition en dernier dans l’ensemble de tous les trajets sur le graphe. Mais, d’ailleurs, de quelles fréquences parle-t-on ? Fréquences par rapport à quoi ?
Cela nous amène à présenter un dernier personnage : les randonnées. Une randonnée est un ensemble de chemins fermés (c’est-à-dire de chemins allant chacun d’un sommet initial à lui même) qui ne se touchent pas forcément les uns les autres sur le graphe. Ceci contraste avec un chemin, qui lui est constitué d’arêtes contiguës sur le graphe, et apparaît donc « d’un seul tenant ».
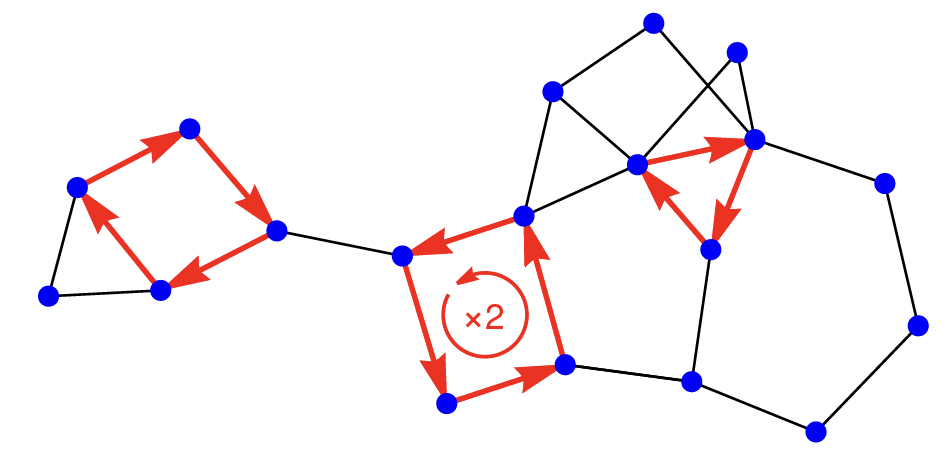
Figure 3 : Une randonnée comportant trois chemins fermés, chacun « d’un seul tenant ».
En particulier, observez qu’un chemin très gentil comme ceux que l’on souhaite étudier est une randonnée qui n’a qu’un seul dernier cycle ! En effet un chemin fermé a toujours un unique dernier cycle et on peut donc dire d’une randonnée comportant plusieurs chemins fermés qu’elle a plusieurs derniers cycles (un par chemin !), une conception qui sera fort pratique par la suite.
Nous souhaitons donc compter les fréquences de chemins fermés finissant par un cycle \(c\) parmi les randonnées. Il faut ainsi dénombrer tous les chemins fermés et faire le quotient de ceux finissant par \(c\) par rapport à tous. Cela semble compliqué… et ça l’est ! Mais on peut être astucieux !
D’abord, imaginons un chemin fermé finissant par \(c\). Si on enlève son dernier cycle \(c\), il restera des chemins potentiellement en plusieurs morceaux éparpillés (donc une randonnée !). Si on s’intéresse aux derniers cycles de chacun de ces morceaux, on peut montrer qu’ils ont forcément au moins un sommet en commun avec le cycle \(c\). En effet, si, par l’absurde, ceci n’était pas vrai alors il y aurait un saut hyperespace dans notre chemin initial, la voiture prenant une trajectoire à la Star Trek ce qui est plutôt difficile à réaliser sur le périphérique ! Si un tel saut existe, on ne serait donc pas en train d’étudier un chemin, c’est absurde.
Ainsi, pour compter les chemins finissant par \(c\), on peut compter les randonnées qui finissent par des derniers cycles qui touchent \(c\). Par le paragraphe précédent, si on leur rajoute \(c\), alors, une telle randonnée devient un chemin et, en démarrant la voiture d’un point de \(c\), le nouveau dernier cycle sera exactement \(c\). La deuxième astuce est en fait de compter le contraire, on va plutôt compter la fréquence de randonnées qui ont des derniers cycles ne touchant pas \(c\) (c’est en fait moins difficile). En notant \(R(L)\) le nombre de randonnées de longueur \(L\), ce nombre de randonnées qui ont des derniers cycles ne touchant pas \(c\) est de \[ \sum_{c_1 \in \cal{C}^c_{yc}} R(L – \ell(c_1))\] où \(\cal{C}^c_{yc}\) est l’ensemble de cycles ne se touchant pas et ne touchant pas \(c\). Pour comprendre le terme \(R (L – \ell (c_1))\), il suffit d’observer que si nous ajoutons \(c_1\) en dernière position d’une randonnée de longueur \(L – \ell(c_1)\) on obtient une randonnée de longueur \(L – \ell (c_1) + \ell (c_1) = L\) dont le dernier cycle \(c_1\) ne touche pas \(c\) par définition de \(\cal{C}^c_{yc}\) : c’est exactement ce que l’on veut. Or le nombre \(R(L)\) de randonnées de longueur \(L\) croît suivant une loi assez simple : \(R(L) \cong a \lambda ^L\). En effet, considérons tout d’abord les chemins. À chaque pas, on a en moyenne \(\lambda\) choix de directions pour la prochaine étape du chemin, donc le nombre total de chemins possibles de longueur \(L\) est de l’ordre de \(\lambda ^L\). Or les randonnées sont des ensembles de chemins et la longueur d’une randonnée est la somme des longueurs des chemins qui la composent. Donc si l’on considère par exemple toutes les randonnées de longueur \(L\) comportant exactement \(3\) chemins de longueurs \(L_1\), \(L_2\) et \(L_3 = L − L_1 − L_2\), le nombre de telles randonnées est de l’ordre de \( \lambda ^{L_1} \lambda ^{L_2} \lambda ^{L_3} = \lambda ^L\). Cette constatation reste inchangée si l’on considère à la place des randonnées de même longueur \(L\) comportant \(1\), \(2\), \(4\) ou plus généralement n’importe quel nombre de chemins, impliquant \(R(L) \cong a \lambda ^L\). Dans cette formule \(a\) est une constante qui peut sembler gênante parce qu’on ne la connaît pas. Mais, on peut s’en débarrasser très simplement car ce qui nous intéresse, ce sont les fréquences. En particulier, on souhaite diviser la formule juste au-dessus par \(R(L)\). La fréquence de randonnées qui ont des derniers cycles ne touchant pas \(c\) est donc d’environ (« environ » car \(R(L) \cong a \lambda ^L\) n’est exact que lorsque \(L\) tend vers l’infini), \[ \sum _{c_1 \in \cal{C}^c_{yc}} \frac{1}{\lambda ^{\ell(c_1)}} \]
En fait, nous avons menti, il y a une petite erreur : on a compté plusieurs fois la même chose… En effet, il se peut qu’une randonnée finisse par plusieurs cycles — pour l’exemple, disons \(2\) cycles \(c_1\) et \(c_2\) — qui ne se touchent pas et ne touchent pas \(c\) non plus. Cette randonnée aurait été comptée \(2\) fois dans notre somme (une fois pour \(c_1\) et une fois pour \(c_2\)). Pour équilibrer, il faut donc la retirer ainsi qu’il faut retirer toutes les paires de cycles ne se touchant pas et ne touchant pas \(c\). Cela amène à une version corrigée de notre fréquence : \[ \sum _{c_1 \in \cal{C}^c_{yc}} \frac{1}{\lambda ^{\ell(c_1)}} − \sum _{c_1, c_2 \in \cal{C}^c_{yc}} \frac{1}{\lambda ^{\ell (c_1) + \ell (c_2)}} .\]
Mais, à nouveau, un souci se pose… Une randonnée qui contiendrait \(3\) derniers cycles (\(c_1\), \(c_2\) et \(c_3\)) ne se touchant pas et ne touchant pas \(c\) aurait été comptée \(3\) fois dans la première somme (une fois pour chaque cycle) et retirée \(3\) fois dans la seconde somme (pour les \(3\) couples possibles avec ces \(3\) cycles). Il faut donc les rajouter à nouveau. Cela amène à écrire \[ \sum _{c_1 \in \cal{C}^c_{yc}} \frac{1}{\lambda ^{\ell(c_1)}} − \sum _{c_1, c_2 \in \cal{C}^c_{yc}} \frac{1}{\lambda ^{\ell (c_1) + \ell (c_2)}} + \sum_{c_1, c_2, c_3 \in \cal{C}^c_{yc}} \frac{1}{\lambda ^{\ell (c_1) + \ell (c_2) + \ell (c_3)} }. \]
Et, vous l’aurez probablement deviné, il va falloir encore rectifier. Ce que l’on est en train de faire s’appelle en mathématique le principe d’inclusion-exclusion, très utile en combinatoire. On compte… mais un peu trop. Donc on retire… mais un peu trop. Donc on rajoute… mais un peu trop. Et ainsi de suite. On va vous rassurer immédiatement : notre graphe étant fini, son nombre de cycles est fini et donc, à un moment, il n’y aura plus de correctifs à appliquer parce qu’il n’existera pas de randonnées avec une trop grande quantité de derniers cycles.
Aussi, en observant l’alternance des signes \(+\) et \(-\) dans notre précédente formule, on peut synthétiser notre fréquence par l’expression suivante \[ \sum_{\cal{C} \subset \cal{C}^c_{yc}} \frac{(-1)^{|\cal{C}|+1}}{\lambda ^{\ell (\cal{C})}} \]
où \(\cal{C}\) est un sous-ensemble de \(\cal{C}^c_{yc}\) autrement dit, \( \cal{C}\) est un nombre (fini) de cycles ne se touchant pas et ne touchant pas \(c\) ; \(|\cal{C}|\)est le nombre de cycles dans cet ensemble et \(\ell (\cal{C})\) la somme des longueurs des cycles dans \(\cal{C}\). Vous pouvez vérifier que si \(\cal{C}^c_{yc}\) ne peut pas contenir plus de \(3\) cycles, on trouve la même formulation que notre précédente approximation. Maintenant, souvenez-vous, c’est la fréquence contraire qui nous intéressait, il faut donc prendre son complément à \(1\), c’est-à-dire \[ 1 − \sum_{\cal{C} \subset \cal{C}^c_{yc}} \frac{(-1)^{|\cal{C}|+1}}{\lambda ^{\ell (\cal{C})}} = \sum_{\cal{C} \subset \cal{C}^c_{yc}} (-1)^{|\cal{C}|+1} \left( \frac{1}{|\cal{C}^c_{yc}|} − \frac{1}{\lambda^{\ell (\cal{C})}} \right) . \]
Cette formule reste cependant toujours difficile à calculer : elle demande de connaître l’ensemble \(\cal{C}^c_{yc}\) et donc presque tous les cycles d’un graphe donné. Mais nous savons qu’il nous faut faire apparaître un déterminant et, croyez-le, il est juste là sous vos yeux, dans cette formule absconse. Si vous êtes familier avec cet outil qu’est le déterminant, vous savez qu’il peut se définir à l’aide d’une somme sur l’ensemble des permutations et d’une signature (qui est une fonction sur les permutations renvoyant \(1\) ou \(-1\)). Un parallèle salvateur peut être effectué : permutation ? Il se trouve qu’un résultat mathématique fort indique qu’une permutation n’est en fait qu’un enchaînement… de cycles ! Une fonction sur les permutations qui renvoie \(1\) ou \(-1\) ? Nous avons ce terme (\(-1)^{|\cal{C}|+1}\) qui joue un rôle similaire ! La formule plus haut est en fait exactement un déterminant ! Il s’agit de celui-ci (qu’on ne démontrera pas, le niveau étant ici beaucoup plus épicé) \[ \det \left( I_{v(G \setminus c)} − \frac{1}{\lambda} A_{G \setminus c} \right) \]
Bien que non-démontrée, on peut expliquer l’apparition de cette matrice \(A_{G \setminus c}\) : c’est justement la matrice du graphe \(G \setminus c\) sur lequel tous les cycles ne touchant pas \(c\) se trouvent (ceux qui nous intéressent).
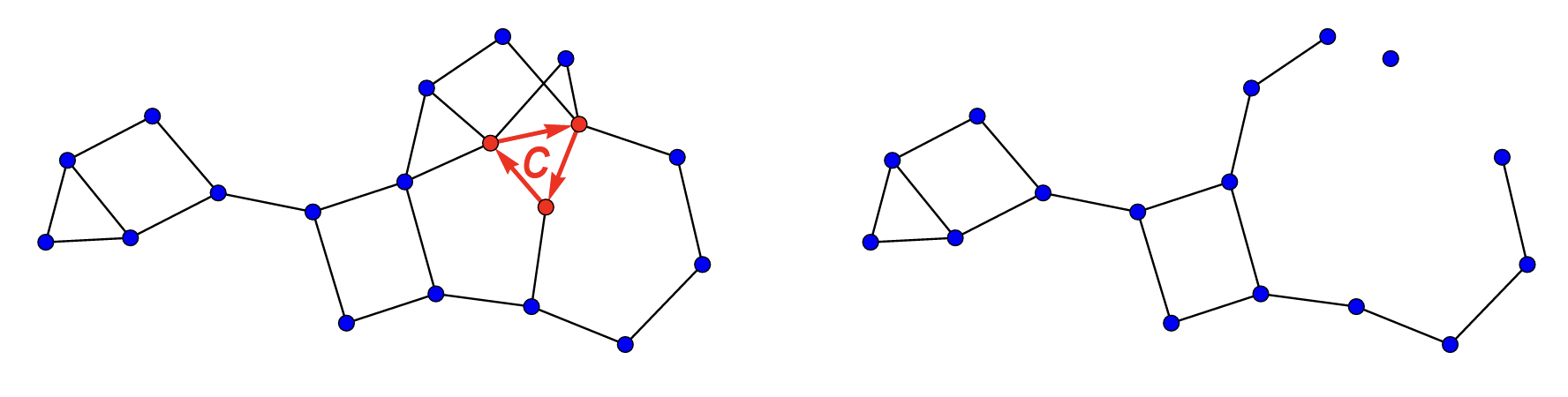
Figure 4 : à gauche un graphe \(G\) et un cycle \(c\). À droite le graphe \(G\setminus c\) où on a enlevé les nœuds visités par \(c\) et toutes les arêtes attenantes à ces nœuds. C’est sur \(G\setminus c\) que se trouvent tous les cycles de \(G\) ne touchant pas \(c\).
C’était l’étape la plus difficile, il nous reste l’ultime marche de notre Everest mathématique : il ne faut pas oublier de rajouter le cycle sur nos randonnées pour avoir effectivement des chemins fermés dont le dernier cycle est \(c\). C’est assez facile, cela prend \(\ell(c) \) arêtes, on multiplie donc par ce « coût », c’est-à-dire \(\lambda ^{-\ell (c)}\). On a ainsi retrouvé la formule recherchée.
Nous avons modélisé le plan de la figure \(1\) par un graphe de \(46\) sommets. Il ressemble à ceci.
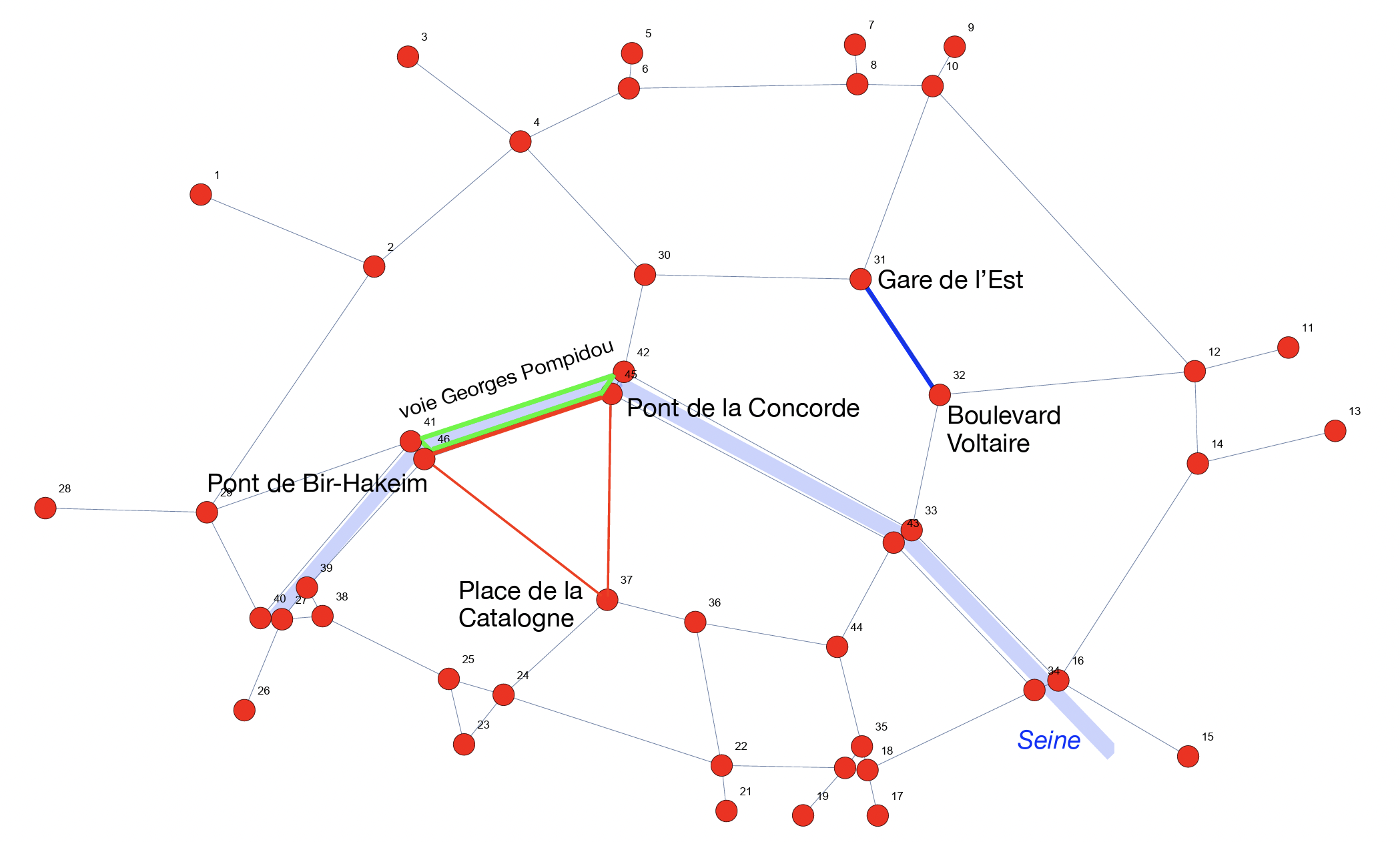
Figure 5 : le graphe correspondant à la figure 1. Ici chaque arête est parcourable dans les deux sens.
Il contient un très grand nombre de cycles simples (plus de \(4200\)). Nous ne vous ferons pas l’affront de vous les présenter. Les cycles les plus courts sont évidemment de longueur \(2\). Un défi serait de trouver un des cycles les plus longs (indice : il ne peut pas passer par plus de \(32\) sommets) ou, par exemple, de trouver les \(5\) triangles. Commençons par analyser les cycles les plus importants d’après notre mesure.
Les cycles les plus importants
Le cycle apparaissant le plus fréquemment dans les trajets en voiture est, selon la formule, l’aller-retour reliant les sommets \(45\) et \(46\) (trait rouge épais sur la carte) pour une valeur d’importance de \(3,45919 \%\). Cela peut sembler faible mais ça ne l’est pas tant que ça relativement au nombre faramineux de cycles différents dans ce graphe. Ce cycle correspond aux quais de Seine, plus précisément la portion côté rive Sud entre le Pont de la Concorde et le Pont de Bir-Hakeim.
Ce résultat indique donc que, structurellement, c’est-à-dire du fait de l’architecture même du réseau d’autoroutes urbaines prévues par Georges Pompidou, près de \(3,5 \%\) des déplacements autoroutiers dans Paris auraient parcouru ce tronçon des quais entre le Pont de la Concorde et le Pont de Bir-Hakeim. Ce cycle est concurrencé de près par un autre cycle d’une importance de \(3,44661\%\) qui est aussi de longueur \(2\). Il se situe entre la Gare de l’Est et le boulevard Voltaire (trait bleu épais sur la carte, voir figure 5). Il nous faudrait départager ces deux cycles, par exemple en considérant des cycles plus longs. Regardons où sont les \(5\) triangles les plus fréquemment parcourus selon notre classement. Le plus important est formé par les sommets \(37\) (Place de Catalogne), \(45\) (Pont de la Concorde) et \(46\) (Pont de Bir-Hakeim) avec une importance de \(1,43263 \%\) (triangle en rouge sur la carte, voir figure 5). Aucun triangle contenant les sommets \(31\) et \(32\) n’existe. Et les quadrilatères dans tout ça ? Le plus important (en vert sur la carte, voir figure 5) pèse pour \(0,70576\%\) et ses côtés sont formés par le Pont de la Concorde (arête \(42-45\)), le Quai Jacques Chirac / Quai d’Orsay (arête \(45-46\)), le Pont de Bir-Hakeim (arête \(46-41\)) et, détail amusant,… une partie de la voie Georges Pompidou (arête \(41-42\)). A contrario, le quadrilatère formé par les sommets \(31\), \(32\), \(12\) et \(10\) a l’importance la plus faible parmi tous les quadrilatères. Cela semble clore le débat : on le comprendra assez aisément, l’axe entre le Pont de la Concorde et le Pont de Bir-Hakeim, particulièrement la rive Sud, serait devenu un axe central du tout Paris selon notre outil de mesure.
Analyse de long cycles
Une observation que l’on peut faire avec les données est que, grosso modo, les cycles les plus importants sont les plus courts. Cela tient à l’intuition suivante : si, à chaque carrefour, l’ensemble des voitures empruntaient les différentes directions avec une probabilité égale, alors plus le cycle considéré est long, c’est-à-dire qu’il passe par de nombreux carrefours, plus la probabilité de le parcourir diminue. La mesure calculée ici montre que cette intuition est généralement correcte. On peut même être plus précis : chaque carrefour doit diviser l’importance d’un cycle par au plus \(\lambda\), la valeur propre dominante de l’ensemble du réseau urbain (qui n’est donc pas déterminée localement par un carrefour, mais globalement à partir de tous). Regardons quelques cycles longs. Comme il y en a beaucoup, plutôt que de lister les différentes valeurs d’importance que l’on peut obtenir, on peut les représenter sous la forme d’un histogramme. L’abscisse de chaque barre indique la valeur d’importance (c’est-à-dire la fréquence avec laquelle un cycle est parcouru par les usagers du réseau), sa hauteur est d’autant plus grande qu’il y a de cycles ayant cette valeur d’importance.
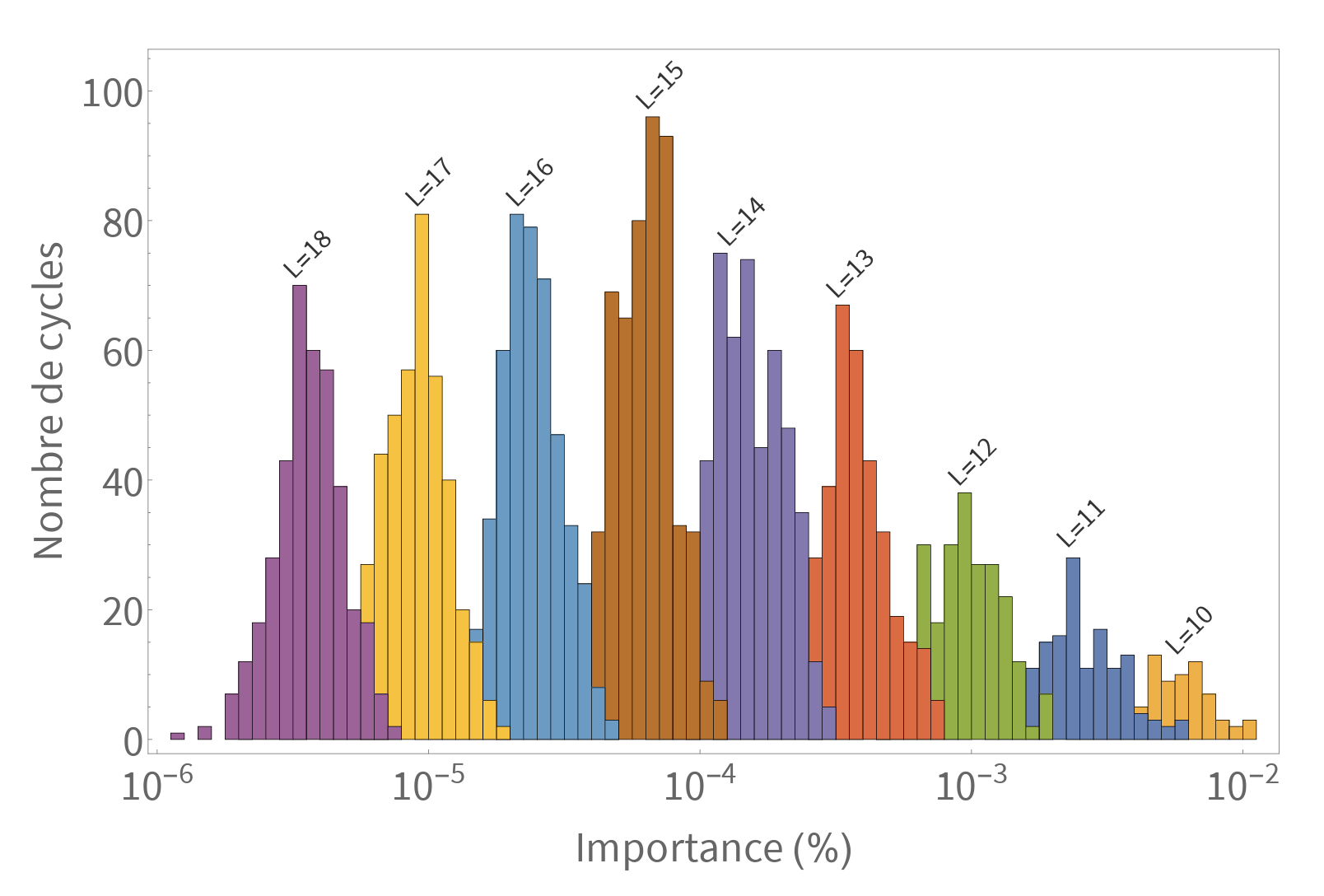
Figure 6 : histogramme d’importance des cycles de longueur \(10\) à \(18\).
Comme prévu, l’importance des cycles longs décroît à peu près avec leur longueur \(L\). Typiquement un cycle de longueur \(L+1\) est \(\sim 2,6\) fois moins important qu’un cycle de longueur \(L\) (en comparaison \(\lambda \sim 3,4\)). Pour une longueur donnée, les cycles les plus importants sont ceux qui passent par les tronçons les plus visités (d’après la mesure d’importance pour les petits cycles). Par exemple, parmi les cycles de longueur \(10\), le plus important parcourt les quais de Seine et le sud Parisien tandis que le moins important, \(5\) fois moins usité, se cantonne à la périphérie de l’Est de Paris.
Conclusion
On pourrait rester sur notre faim (fin…) par rapport aux conclusions de notre étude. Pourquoi ne pas mettre des poids sur certaines arêtes parce qu’ici les autoroutes sont en \(2 \times 2\) voies ou là en \(2 \times 3\) ? Pourquoi ne pas faire de différences entre les zones résidentielles, commerciales ou industrielles dont les trafics sont, par nature, différents ?
Relativisons, l’évolution et la complexification d’un modèle font partie intégrante d’un travail de recherche. Et, par définition, un modèle n’est pas la réalité : il n’en est qu’un reflet possédant toujours des limites, des défauts. De plus, on a choisi ici un sujet d’étude relativement simple à exposer pour passer plus de temps sur l’analyse du modèle, et menant à une formule finale aisément calculable par un ordinateur. Des modèles plus ambitieux nécessitent des simulations avancées et sont souvent basés sur des heuristiques. Cela nous a aussi permis de construire une histoire où nous avons rencontré plusieurs personnages interagissant entre eux par des formules ou des raisonnements.
Mais la force des mathématiques est son universalité : les graphes ont des applications multiples. C’est donc aussi le cas de notre notion d’importance de cycles. Cette quantité que nous calculons peut se révéler utile dans d’autres domaines que l’urbanisme : la dynamique sociale (en étudiant les interactions entre personnes via les réseaux sociaux), la finance (en étudiant les flux d’argent entre acteurs économiques) ou la santé (en étudiant les molécules médicamenteuses). Comment choisir la molécule à tester pour concevoir le prochain médicament qui soignera une certaine maladie ? Comment éviter une réaction en chaîne économique qui pourrait déstabiliser une certaine région du monde ? Qui fait le plus circuler l’information sur un certain réseau social ? Une opinion peut être proposée pour chacune de ces questions avec l’outil que nous vous avons présenté. Mais encore une fois, cette opinion n’est pas la vérité. Il faut toujours chercher à la critiquer, l’améliorer et ne pas s’arrêter en si bon chemin.
Une introduction rigoureuse aux outils mathématiques utilisés ici sur le site de Xavier Viennot, pionnier français de la combinatoire.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Pierre-Louis Giscard
Maître de conférences au Laboratoire de Mathématiques Pures et Appliquées Joseph Liouville (LMPA) de l'Université Littoral Côte d'Opale à Calais.

