
Quel trajet optimal pour passer au moins une fois par toutes les lignes de métro ?
Comment trouver un tel trajet optimal ? Cette question est semblable à un défi figurant dans le fameux « Livre Guinness des records », où il faut passer par toutes les stations d’une ville le plus rapidement possible. Le record actuel pour Paris semble être détenu par un certain Adham Fisher en 2011, ayant mis 13h37 pour passer par les 302 stations. Cette question apparaît également dans la culture populaire (challenges d’étudiants comme le Défi Métro, vidéos sur Youtube Faire toutes les lignes du métro en un seul jour, exercices de prose comme le poème de métro de l’Oulipo) mais aussi dans la littérature scientifique (thèse, articles scientifiques…).
[SPOILER] À Paris, il est possible de passer par les 16 lignes de métro en seulement 26 étapes. Plus surprenant encore, si l’on désire emprunter les 5 lignes de RER en plus des 16 lignes de métro, il est toujours possible de le faire en 26 étapes !
Trouver ce trajet optimal est en fait assez complexe et nécessite des outils avancés d’une branche de l’informatique et des mathématiques discrètes : la Recherche Opérationnelle. Un objet classique et fondamental dans cette branche des mathématiques est le graphe.
Un réseau de métro peut naturellement être modélisé par un graphe, où chaque station est représentée par un nœud (ou sommet) et où se trouve un arc (ou arête) entre deux sommets s’il existe une ligne reliant directement les deux stations correspondantes. Les arcs auront de plus un label (ou une couleur) représentant le numéro de la ligne comme sur la carte de métro ci-dessous. De plus, il est possible d’ajouter une orientation d’un sommet à l’autre pour chaque arc, on parle alors de graphe orienté. Par exemple, dans le cas d’une représentation par un graphe orienté du métro parisien, il y aurait deux arcs avec un label « bleu » (ou « ligne 2 ») entre le sommet « Ménilmontant » et le sommet « Père Lachaise » car il est possible d’effectuer ce trajet dans les deux sens et un seul arc sur certaines portions de la ligne 10 et de la ligne 7 bis pour lesquelles le trajet ne peut s’effectuer que dans un seul sens.
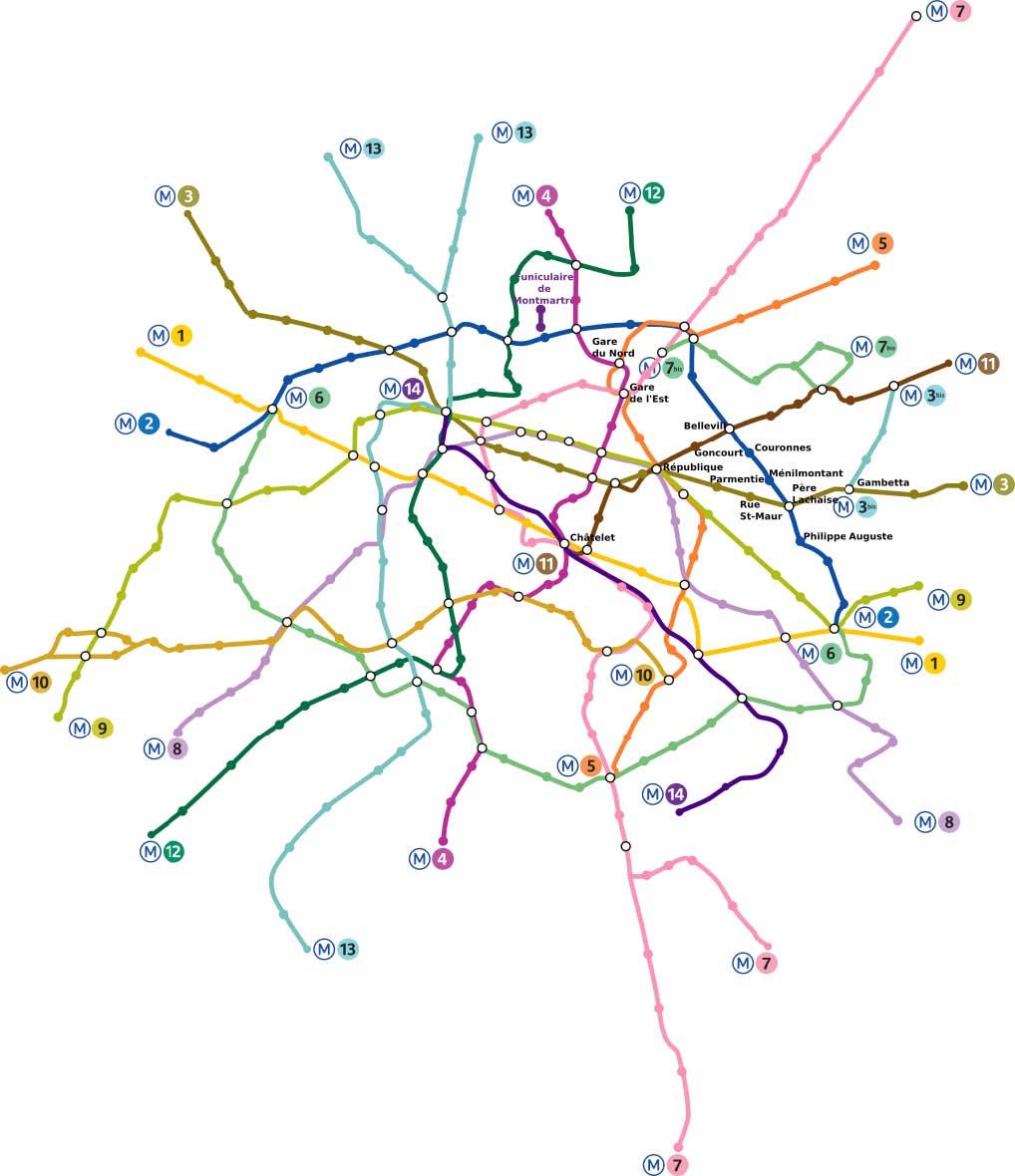
Carte du métro parisien.
Une marche dans un graphe est une suite de sommets telle que deux sommets consécutifs sont reliés par un arc (un sommet peut apparaître plusieurs fois dans une marche).
Notre problème revient alors à trouver la marche la plus courte utilisant au moins une fois toutes les couleurs du graphe. Ce problème est connu sous le nom du problème du postier rural (« Generalized Directed Rural Postman »), dans la catégorie assez large des problèmes de tournées sur arcs (« Arc Routing Problems »), problèmes où le but est de trouver des chemins optimaux dans les graphes en se focalisant sur les propriétés des arêtes plutôt que sur les sommets (par exemple déterminer les chemins pour de la livraison de courrier, la collecte de déchets, des relevés de compteurs, etc).
Malheureusement, ce problème entre dans la catégorie des problèmes dits NP-difficiles.
Cependant, il faut quand même tenter d’y répondre ! Notons que chercher le chemin le plus court entre deux points (question que l’on se pose régulièrement dans la vie de tous les jours, par exemple lors de la recherche d’un trajet sur une carte ou la recherche d’un itinéraire en transport en commun) est par contre un problème « facile » : il est possible d’y répondre de manière exacte dans un temps raisonnable. Une simple contrainte supplémentaire (comme par exemple utiliser au moins une fois toutes les couleurs du graphe) change donc la « complexité » du problème. Pour résoudre notre problème, nous en avons proposé une formulation sous forme d’un programme linéaire en nombres entiers et l’avons appliqué aux réseaux des métros de Paris et de Tokyo.
La programmation linéaire consiste à optimiser une fonction d’objectif à plusieurs variables avec des contraintes sur ces variables. Si l’on est assuré que les variables ont des valeurs réelles et que les contraintes et l’objectif ont une forme linéaire (un polynôme de degré 0 ou 1 par exemple), alors il est possible de trouver l’optimum dans un temps polynomial, c’est-à-dire avec un nombre d’opérations dépendant polynomialement de la taille de l’instance.
Nous illustrons cette technique avec un exemple simplifié : supposons que l’on souhaite trouver le plus court chemin dans un graphe (par exemple celui du métro), entre le point s et le point t. On note (i,j) un arc allant du sommet i au sommet j et on note A l’ensemble des arcs présents dans le graphe. On introduit autant de variables que d’arcs dans le graphe, c’est-à-dire que pour chaque arc (i,j), on définit une variable \(x_{i,j}\), pouvant valoir 1 (l’arc est choisi dans la solution) ou 0 (l’arc n’est pas choisi). Le but étant d’avoir le chemin le plus court, notre objectif sera de minimiser la somme de toutes ces variables. Reste maintenant à ajouter des contraintes pour avoir 1) un chemin et 2) allant de s à t. Pour cet exemple, cela reste assez simple. On ajoutera les contraintes suivantes :
\(\sum_{j\,tel\,que\,(s,j) \in A} x_{s,j} – \sum_{j\,tel\,que\,(j,s) \in A} x_{j,s} = 1\) (on part de s : il doit exister un arc dans la solution partant de s)
\(\sum_{j\,tel\,que\,(t,j) \in A} x_{t,j} – \sum_{j\,tel\,que\,(j,t) \in A} x_{j,t} = -1\) (on arrive en t : il doit exister un arc dans la solution arrivant en t)
\(\sum_{j\,tel\,que\,(i,j) \in A} x_{i,j} – \sum_{j\,tel\,que\,(j,i) \in A} x_{j,i} = 0\), pour chaque sommet i différent de s et t (le nombre d’arcs arrivant en i doit être le même que le nombre d’arcs partant de i)
\(x_{i,j} = {0,1}\), pour chaque arc (i,j) (un arc peut être pris ou non).
Notons qu’il est facilement possible de rajouter des « poids » sur les arêtes (représentant des durées ou des coûts par exemple). On cherchera alors à minimiser la somme des produits entre les variables d’arcs et le poids de l’arc, les contraintes restent inchangées.
Combien cela fait-il de contraintes ? Notons n le nombre de sommets et m le nombre d’arcs. La 1re formule concerne le sommet de départ s, la 2e formule concerne le sommet d’arrivée t, la 3e concerne tous les n-2 autres sommets, ces 3 formules correspondent donc à n contraintes. La 4e formule concerne chaque arc, elle correspond donc à m contraintes. Nous avons donc au total n + m contraintes.
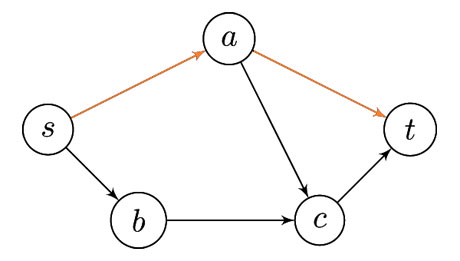
Par exemple, pour le graphe simple de la figure ci-dessus, nous aurions une solution allant de s à t en passant par a plutôt que par b et c.
La solution est donc \(x_{s,a}\) \(=\) \(x_{a,t}\) \(= 1\)
et \(x_{s,b} = x_{b,c} = x_{a,c} = x_{c,t} = 0.\)
On vérifie que les contraintes correspondant à ce graphe sont satisfaites :
\((1)\) \(x_{s,a}\)\( + x_{s,b} = 1\)
\((2) -\)\(x_{a,t}\)\( – x_{c,t} = -1\)
\((3a)\)\( x_{a,t}\)\( + x_{a,c} -\)\( x_{s,a}\) \(= 1 + 0 – 1 = 0\)
\((3b) x_{b,c} – x_{s,b} = 0 – 0 = 0\)
\((3c) x_{c,t} – x_{a,c} – x_{b,c} = 0 – 0 – 0 = 0\)
Dans le cas précis du problème du plus court chemin, on peut remplacer les contraintes \(x_{i,j} = {0,1}\) par des contraintes \(x_{i,j} ≥ 0\) (les variables peuvent également être non entières) et continuer d’avoir une solution optimale où les variables prendront les valeurs 0 ou 1 (mais ce n’est pas un résultat trivial et prouver cela est hors sujet dans notre cas). Toutefois, dans le cas général, dès que l’on restreint des variables à prendre des valeurs entières uniquement, le problème devient également NP-difficile. Cependant, il existe de nombreux outils, souvent issus du monde académique, permettant de résoudre plutôt efficacement ces problèmes, comme GUROBI, CPLEX, SCIP…
Notons qu’il existe d’autres manières d’encoder le problème du plus court chemin, notamment en utilisant seulement n variables. Notons également que pour le cas du problème du plus court chemin, il existe plusieurs algorithmes dits combinatoires (c’est-à-dire explicitement décrits pour résoudre ce problème) permettant de trouver le plus court chemin sans passer par la programmation linéaire, par exemple l’algorithme dit de Dijkstra. Comme l’a remarqué Jeff Erickson dans son livre, cet algorithme a été découvert et redécouvert par plusieurs personnes indépendamment et est maintenant connu sous le nom d’algorithme de Dijkstra suivant la loi de Stigler (et que personne ne veut utiliser le nom d’« algorithme de Leyzorek-Gray-Johnson-Ladew-Meaker-Petry-Seitz-Dantzig-Dijkstra-Minty-Whiting-Hillier »). Cependant, pour de nombreux autres problèmes, la manière la plus efficace de trouver une solution optimale consiste à formuler le problème sous forme de programmation linéaire puis d’utiliser un outil permettant de résoudre cette formulation.
Mais revenons à notre problème du Generalized Directed Rural Postman. On pourrait partir de la même formulation que celle du plus court chemin et ajouter des contraintes supplémentaires assurant que pour chaque ligne de métro, au moins une des portions fasse partie de la solution (par exemple en ajoutant une contrainte disant que pour chaque ligne de métro, la somme des variables des arcs la composant doit être supérieure ou égale à 1). Malheureusement, ce n’est pas aussi simple et suffisant : une solution pourrait alors être non connectée, c’est-à-dire composée d’un chemin mais aussi de cycles disjoints de ce chemin (ceux-ci satisfont la contrainte disant que la somme des arcs sortants doit être la même que celle des arcs sortant d’un sommet !). On doit alors ajouter des contraintes et variables supplémentaires, pour éviter cela et demander une solution connexe : la formulation requiert alors de l’ordre de n + 2m variables et 3n + l + m contraintes, avec n le nombre de stations, m le nombre de tronçons de lignes et l le nombre de lignes. Cette formulation permet d’obtenir une solution optimale à notre problème dans un temps rapide par exemple avec CPLEX — entre quelques minutes et quelques heures selon le problème demandé, malgré la NP-difficulté du problème.
On obtient les résultats suivants appliqués au métro de Paris. Pour passer par les 16 lignes du métro parisien, il y a besoin de 26 étapes (une étape correspond à un arc reliant deux stations). Une possibilité parmi de nombreuses autres est de partir de la station Cambronne jusqu’à Saint-Fargeau (voir table 1 et figure 1). À noter le trajet aller-retour sur la section La Motte-Picquet Grenelle – Avenue Émile Zola, car le trajet est possible dans les deux sens entre ces deux stations. Notons aussi qu’il est impossible d’effectuer le même trajet dans l’autre sens avec le même nombre d’étapes car celui-ci passe par des sections de lignes en sens unique !
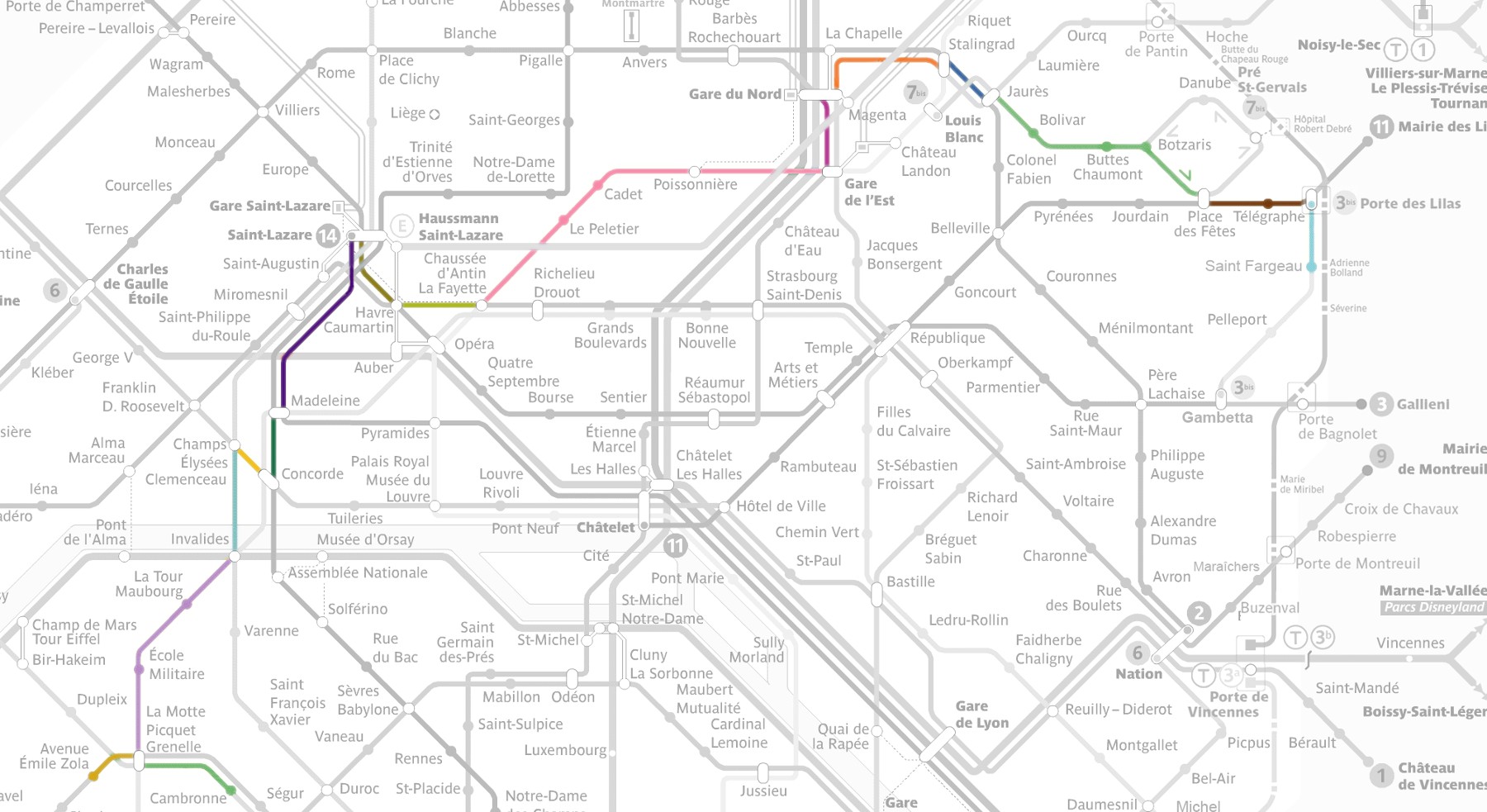
Figure 1.
| Étape | Départ | Arrivée | Ligne |
|---|---|---|---|
| 1 | Cambronne | La Motte-Picquet – Grenelle | 6 |
| 2 | La Motte-Picquet – Grenelle | Avenue Emile Zola | 10 |
| 3 | Avenue Emile Zola | La Motte-Picquet – Grenelle | 10 |
| 4 | La Motte-Picquet – Grenelle | Ecole Militaire | 8 |
| 5 | Ecole Militaire | La Tour-Maubourg | 8 |
| 6 | La Tour-Maubourg | Invalides | 8 |
| 7 | Invalides | Champs Elysées – Clémenceau | 13 |
| 8 | Champs Elysées – Clémenceau | Concorde | 1 |
| 9 | Concorde | Madeleine | 12 |
| 10 | Madeleine | Saint-Lazare | 14 |
| 11 | Saint-Lazare | Havre – Caumartin | 3 |
| 12 | Havre – Caumartin | Chaussée d’Antin – La Fayette | 9 |
| 13 | Chaussée d’Antin – La Fayette | Le Peletier | 7 |
| 14 | Le Peletier | Cadet | 7 |
| 15 | Cadet | Poissonnière | 7 |
| 16 | Poissonnière | Gare de l’Est | 7 |
| 17 | Gare de l’Est | Gare du Nord | 4 |
| 18 | Gare du Nord | Stalingrad | 5 |
| 19 | Stalingrad | Jaurès | 2 |
| 20 | Jaurès | Bolivar | 7bis |
| 21 | Bolivar | Buttes Chaumont | 7bis |
| 22 | Buttes Chaumont | Botzaris | 7bis |
| 23 | Botzaris | Place des Fêtes | 7bis |
| 24 | Place des Fêtes | Télégraphe | 11 |
| 25 | Télégraphe | Porte des Lilas | 11 |
| 26 | Porte des Lilas | Saint-Fargeau | 3bis |
| Table 1. | |||
Si l’on ajoute la contrainte de passer également par les 5 lignes de RER, de manière surprenante, il est toujours possible de le faire en 26 étapes ! (voir table 2 et figure 2). En effet, le RER permet de « sauter » plus rapidement d’un endroit à l’autre en évitant de rester longtemps sur la même ligne.
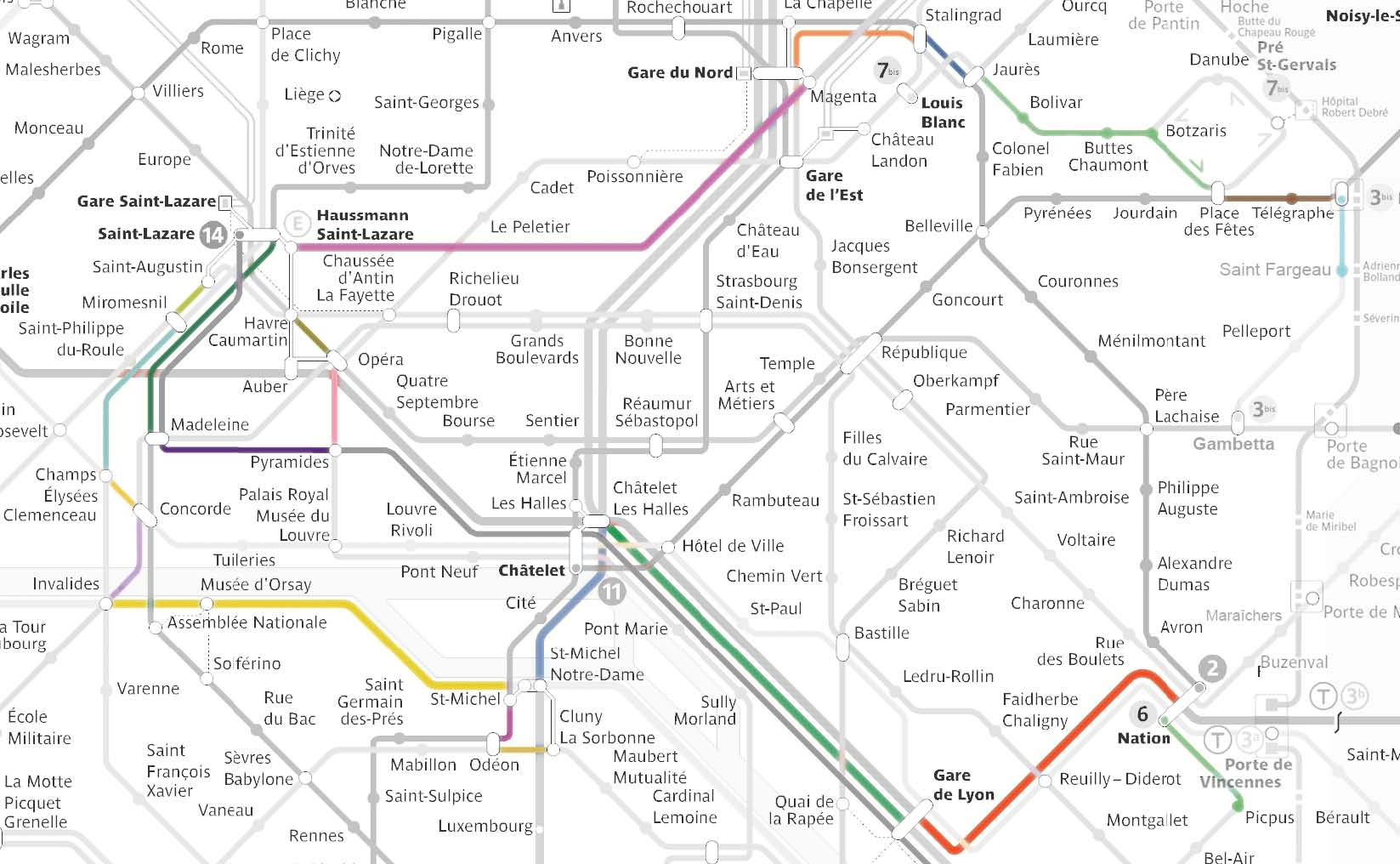
Figure 2.
| Étape | Départ | Arrivée | Ligne |
|---|---|---|---|
| 1 | Picpus | Nation | 6 |
| 2 | Nation | Gare de Lyon | A |
| 3 | Gare de Lyon | Châtelet – Les Halles | D |
| 4 | Châtelet – Les Halles | Saint-Michel – Notre-Dame | B |
| 5 | Saint-Michel | Odéon | 4 |
| 6 | Odéon | Cluny – La Sorbonne | 10 |
| 7 | Saint-Michel – Notre-Dame | Musée d’Orsay | C |
| 8 | Musée d’Orsay | Invalides | C |
| 9 | Invalides | Concorde | 8 |
| 10 | Concorde | Champs Elysées – Clémenceau | 1 |
| 11 | Champs Elysées – Clémenceau | Miromesnil | 13 |
| 12 | Miromesnil | Saint-Augustin | 9 |
| 13 | Saint-Lazare | Madeleine | 12 |
| 14 | Madeleine | Pyramides | 14 |
| 15 | Pyramides | Opéra | 7 |
| 16 | Opéra | Havre – Caumartin | 3 |
| 17 | Haussmann St-Lazare | Magenta | E |
| 18 | Gare du Nord | Stalingrad | 5 |
| 19 | Stalingrad | Jaurès | 2 |
| 20 | Jaurès | Bolivar | 7bis |
| 21 | Bolivar | Buttes Chaumont | 7bis |
| 22 | Buttes Chaumont | Botzaris | 7bis |
| 23 | Botzaris | Place des Fêtes | 7bis |
| 24 | Place des Fêtes | Télégraphe | 11 |
| 25 | Télégraphe | Porte des Lilas | 11 |
| 26 | Porte des Lilas | Saint-Fargeau | 3bis |
| Table 2. | |||
Cependant, on peut observer que dans ces solutions, on emprunte plusieurs fois la même station ! Si on veut interdire cela, alors on augmente la longueur du voyage : on a besoin de 27 étapes (au lieu de 26) pour visiter toutes les lignes de métro et de 29 étapes (au lieu de 26) pour visiter toutes les lignes de métro et de RER.
Nous avons également étudié le problème lorsque l’on veut revenir au point de départ (on parle alors de cycle dans un graphe) : notons qu’il est alors possible de partir de n’importe quelle station de cette solution pour effectuer le trajet ! Comme il faut pouvoir revenir au point de départ, le trajet sera forcément plus long : on a besoin de 39 étapes pour visiter toutes les lignes de métro (voir figure 3 et table 3) et de 33 étapes pour visiter toutes les lignes de métro et de RER (oui, c’est plus rapide de passer par plus de lignes !)
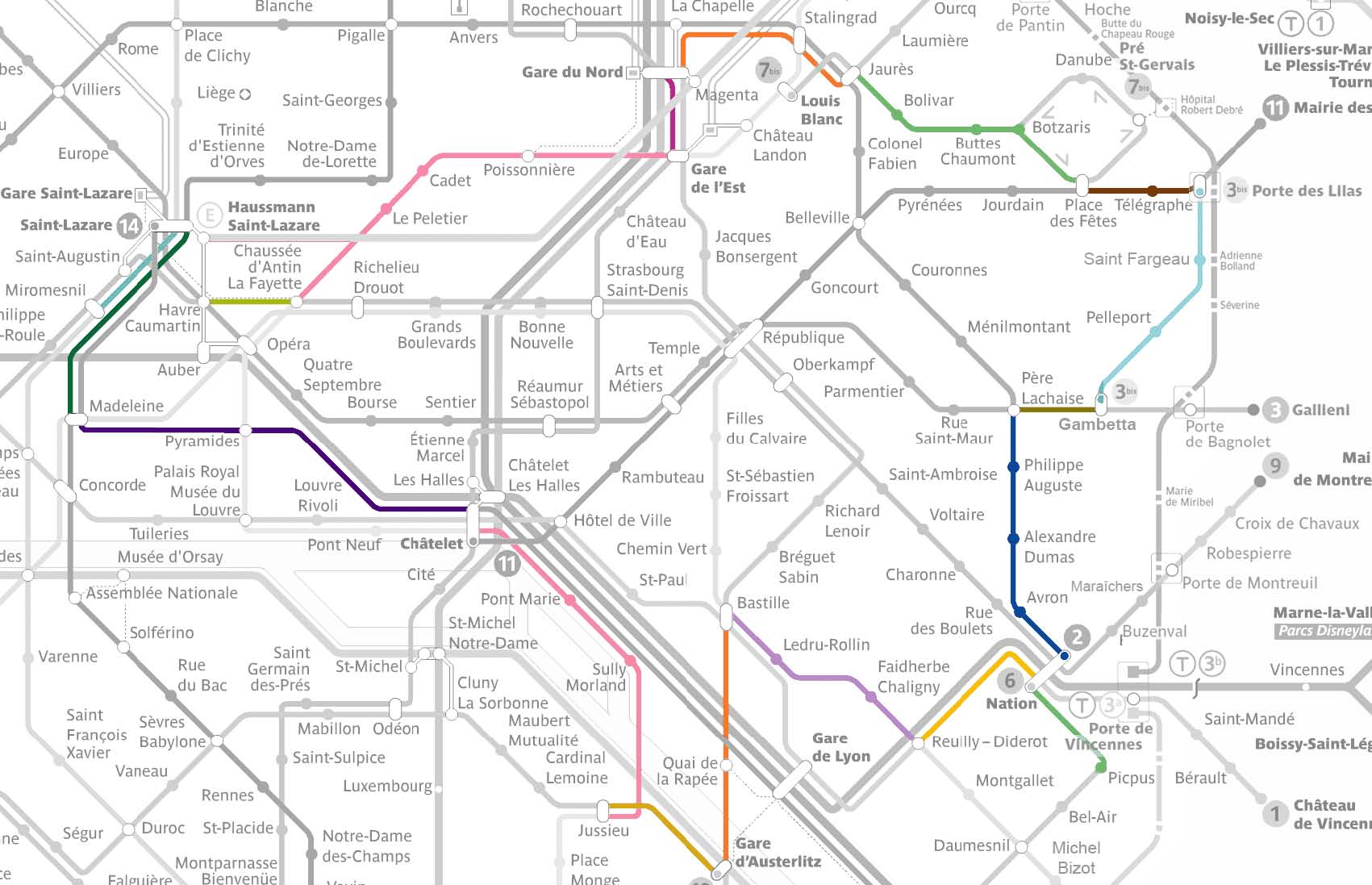
Figure 3.
| Étape | Départ | Arrivée | Ligne |
|---|---|---|---|
| 1 | Gambetta | Père Lachaise | 3 |
| 2 | Père Lachaise | Philippe Auguste | 2 |
| 3 | Philippe Auguste | Alexandre Dumas | 2 |
| 4 | Alexandre Dumas | Avron | 2 |
| 5 | Avron | Nation | 2 |
| 6 | Nation | Picpus | 6 |
| 7 | Picpus | Nation | 6 |
| 8 | Nation | Reuilly – Diderot | 1 |
| 9 | Reuilly – Diderot | Faidherbe – Chaligny | 8 |
| 10 | Faidherbe – Chaligny | Ledru Rollin | 8 |
| 11 | Ledru Rollin | Bastille | 8 |
| 12 | Bastille | Quai de la Rapée | 5 |
| 13 | Quai de la Rapée | Gare d’Austerlitz | 5 |
| 14 | Gare d’Austerlitz | Jussieu | 10 |
| 15 | Jussieu | Sully – Morland | 7 |
| 16 | Sully – Morland | Pont Marie | 7 |
| 17 | Pont Marie | Châtelet | 7 |
| 18 | Châtelet | Pyramides | 14 |
| 19 | Pyramides | Madeleine | 14 |
| 20 | Madeleine | Saint-Lazare | 12 |
| 21 | Saint-Lazare | Miromesnil | 13 |
| 22 | Miromesnil | Saint-Lazare | 13 |
| 23 | Havre – Caumartin | Chaussée d’Antin – La Fayette | 9 |
| 24 | Chaussée d’Antin – La Fayette | Le Peletier | 7 |
| 25 | Le Peletier | Cadet | 7 |
| 26 | Cadet | Poissonnière | 7 |
| 27 | Poissonnière | Gare de l’Est | 7 |
| 28 | Gare de l’Est | Gare du Nord | 4 |
| 29 | Gare du Nord | Stalingrad | 5 |
| 30 | Stalingrad | Jaurès | 5 |
| 31 | Jaurès | Bolivar | 7bis |
| 32 | Bolivar | Buttes Chaumont | 7bis |
| 33 | Buttes Chaumont | Botzaris | 7bis |
| 34 | Botzaris | Place des Fêtes | 7bis |
| 35 | Place des Fêtes | Télégraphe | 11 |
| 36 | Télégraphe | Porte des Lilas | 11 |
| 37 | Porte des Lilas | Saint-Fargeau | 3bis |
| 38 | Saint-Fargeau | Pelleport | 3bis |
| 39 | Pelleport | Gambetta | 3bis |
| Table 3. | |||
L’auteur de cette note a effectué un de ces trajets accompagné d’un cobaye volontaire. De plus, deux autres personnes ayant vu la note scientifique en ligne ont également effectué un de ces trajets. L’ensemble de ces personnes était ravi de ces voyages originaux !
Répondre à cette question « amusante » nous permet en réalité de voir que ce n’était pas si « facile ». Nous avons ainsi pu présenter ce qu’était un problème NP-complet et leur résolution via des outils dits de « programmation mathématique », une approche classique pour résoudre beaucoup d’autres problèmes.
Dans notre cas, il serait possible de rendre plus réaliste ce problème en prenant en compte les temps effectifs de trajet (prendre un tronçon de RER prend plus de temps qu’un tronçon de métro), les temps de changement (on voudra certainement éviter Châtelet dans ce cas !). On pourrait rendre le tout plus intéressant pour les touristes en ajoutant des bonus pour les stations remarquables (le domaine du « Tourist Trip Design » existe également dans la recherche opérationnelle). Leur prise en compte ne demanderait pas de modification majeure pour la résolution informatique, mais, comme bien souvent dans ce domaine, cela nécessiterait une obtention délicate des données !
- Jacques Jouet and Pierre Rosenstiehl. Frise du métro parisien. Number 97. La Bibliothèque Oulipienne, 1998
- Wolfgang Welz. Robot Tour Planning with High Determination Costs. PhD thesis, TU Berlin, 2014
- Michael Drexl. On the generalized directed rural postman problem. JORS, 65(8):1143–1154, 2014
- Ángel Corberán and Gilbert Laporte. Arc routing: problems, methods, and applications. SIAM, 2014
- Jeff Erickson. Linear Programming. Lecture Notes, 2018 (PDF)
- Florian Sikora, The shortest way to visit all metro lines in Paris, 2017
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

