Quand le vent nous fait vibrer

Action d’un fluide sur un obstacle

Lorsqu’un écoulement de fluide rencontre un obstacle, le fluide exerce une force sur ce dernier. Un exemple typique est la force de portance qui permet aux ailes d’un avion de contrebalancer son poids (voir aussi l’article « la forme idéale d’une aile »).  Dans le cas du pont de Tacoma, cette force est manifestement périodique au cours du temps et a créé un mouvement d’oscillation de la structure du pont, comme le montre le film tourné lors de l’évènement. Une première question à se poser pour expliquer le phénomène concerne donc la caractérisation des actions du vent sur le pont : comment un vent uniforme (en espace) et permanent (en temps) peut-il donner naissance à un effort provoquant des oscillations ?

Lorsqu’on s’intéresse à modéliser un phénomène physique, on fait couramment appel au principe de Curie pour simplifier le problème. Celui-ci stipule que « les effets ont au moins les symétries de causes » (voir la page wikipedia sur le principe de Curie). Ainsi, on peut s’attendre à ce qu’un obstacle symétrique, placé dans un écoulement amont (c’est-à-dire avant perturbation) également symétrique, génèrent un écoulement symétrique, et par suite des efforts symétriques. Le pont de Tacoma a un tablier en forme de H, donc symétrique, comme le montre le schéma suivant :

Il a pourtant subi des efforts non symétriques provenant du vent pour générer le mouvement d’oscillation. Comment expliquer ce paradoxe ? Pour simplifier, considérons un obstacle circulaire, on peut alors s’attendre à un écoulement symétrique, similaire à celui représenté sur la figure suivante :

Pourtant, si on réalise l’expérience en laboratoire, on constate l’apparition d’un écoulement totalement différent et non-symétrique, appelé allée de Von Karman :

Ce type d’écoulement peut facilement s’observer en regardant les tourbillons créés par une rivière derrière une pile de pont. Le principe de Curie est-il mis en défaut ? En fait, il n’en est rien : la symétrie du problème réel n’est qu’apparence, il existe forcément des défauts minuscules sur l’obstacle et des perturbations dans l’écoulement amont qui brisent la symétrie. La non-linéarité des équations de Navier-Stokes régissant l’écoulement amplifient ces petites perturbations et donnent naissance à des tourbillons alternatifs. C’est le fameux « effet papillon », créateur de désordre au sein des fluides. Seul le problème théorique issu de notre esprit présente une symétrie. D’ailleurs, lorsqu’on réalise une simulation numérique du phénomène sur ordinateur, on retrouve bien ces oscillations caractéristiques alternées car les erreurs d’arrondis dans le calcul suffisent à briser la symétrie de la simulation !

Résonance de la structure

Effondrement du pont de Tacoma en novembre 1940.
Source Photo : PICRYL – Photographie du domaine public – image historique de l’État de Washington, États-Unis, libre d’utilisation, sans restrictions de droits d’auteur.

Dans le cas du pont de Tacoma, des oscillations similaires ont bien eu lieu au sein de l’écoulement. Elles ont généré des efforts périodiques sur le pont, dus à la naissance des tourbillons de part et d’autre du tablier. Cette explication était déjà bien connue dans les années 1940 et a été considérée, dans un premier temps, comme étant à l’origine des mouvements du pont, à cause du phénomène de résonance. Lorsqu’un système déformable, comme par exemple un ressort attaché à une masse, est soumis à une force excitatrice périodique, l’amplitude du mouvement dépend de la fréquence de l’excitation. Notamment, lorsque celle-ci s’approche d’une fréquence particulière appelée fréquence propre du système, le mouvement est amplifié de façon spectaculaire. C’est le phénomène de résonance. Dans le cas d’un simple ressort, la fréquence propre a pour valeur la racine carrée du quotient de la raideur par la masse, divisée par 2Pi. Pour le pont de Tacoma, l’analyse est bien entendu plus complexe et fait intervenir les caractéristiques des matériaux, la forme des pièces mécaniques, etc. Néanmoins, le phénomène reste similaire et les études d’ingénierie ont montré la présence d’une fréquence propre de l’ordre de 0.2 Hz pour ce pont. Cependant, cette cause a rapidement été écartée par la commission qui a enquêté sur les mouvements du pont de Tacoma, car la fréquence d’apparition des tourbillons ce jour-là, liée à la vitesse du vent, était d’environ 1 Hz. Il est toutefois amusant de constater que, dans de nombreux ouvrages d’ingénierie mécanique, on a continué à mettre en avant le cas du pont de Tacoma comme une illustration du phénomène de résonance. Cependant, si la résonance de la structure du pont n’est pas responsable, comment expliquer ce qui s’est déroulé ce jour-là ?

Interactions entre fluide et structure déformable

L’origine du phénomène ne vient pas des seules caractéristiques de la structure du pont, mais d’une amplification progressive des interactions entre le vent et le pont en mouvement. Pour l’expliquer, il faut analyser en détail comment les deux sous-systèmes (fluide et structure) interagissent. Deux conditions définissent le couplage : la condition cinématique stipule que le déplacement de la structure est égal au déplacement du fluide au contact (pas de création de vide à l’interface), tandis que la condition dynamique traduit le fait que la force exercée par le fluide sur la structure est opposée à la réaction de la structure sur le fluide (équilibre des forces à l’interface). De manière intuitive, on peut ainsi dire que le fluide exerce une force sur la structure qui se déplace et, en retour, cette dernière pousse ou tire le fluide, ce qui va modifier sa force, etc. Cette boucle de couplage est illustrée par le schéma ci-dessous :

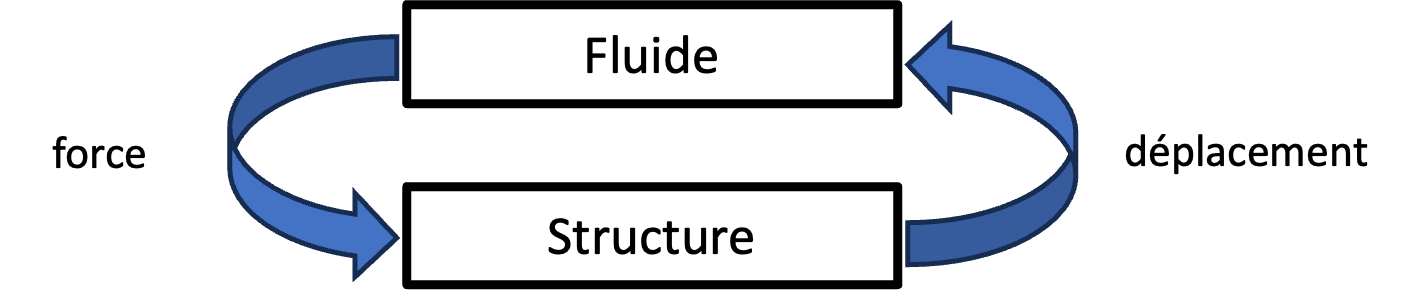
Le couplage entre les deux sous-systèmes peut être stabilisateur si la force du fluide s’oppose au déplacement de la structure, ou au contraire amplificateur si le mouvement de la structure augmente la force exercée par le fluide. L’analyse théorique de ces systèmes est généralement complexe et on a souvent recours à la simulation numérique pour comprendre les phénomènes en jeu. Lorsqu’on souhaite simuler un tel problème, il faut résoudre les équations régissant le fluide, celles correspondant à la structure et, de plus, les deux conditions de couplages qui rendent les deux sous-systèmes interdépendants.

Instabilités et flottement

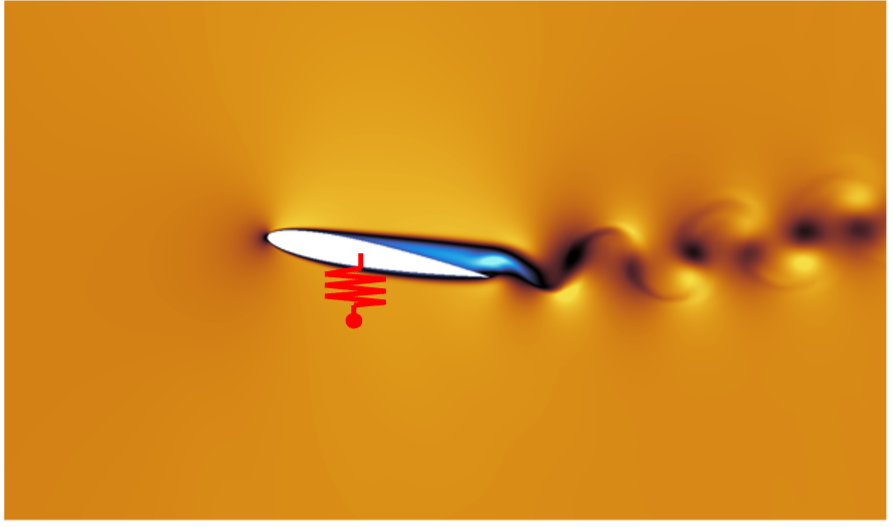
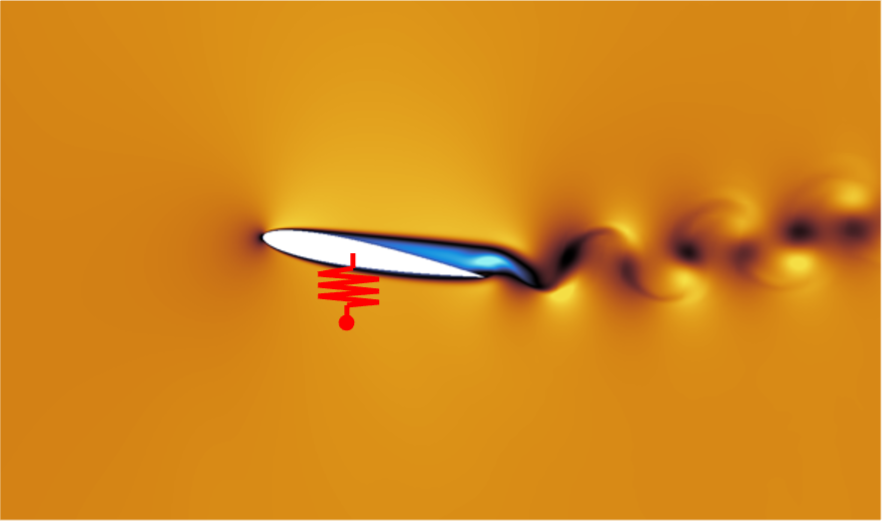
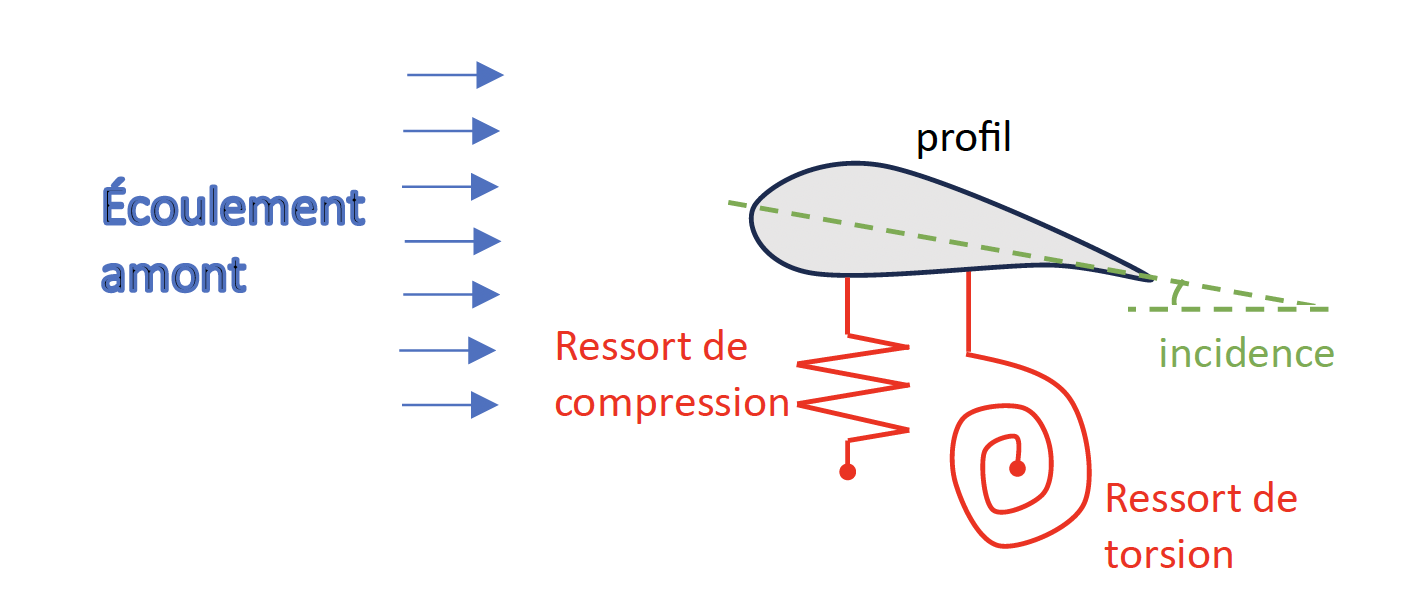
Examinons maintenant comment ce couplage entre un fluide et une structure élastique peut produire des vibrations, en commençant par s’intéresser au cas des ailes d’avion. En effet, les ailes d’un avion peuvent se déformer sous l’action de l’air et connaissent également des phénomènes de mouvements oscillants, appelés flottement, comme le montrent certaines vidéos (voir par exemple ce film sur le flottement des ailes). La déformation globale d’une aile d’avion est un problème relativement complexe mais, pour analyser le phénomène qui nous intéresse ici, on peut étudier une configuration simplifiée 2D correspondant à une tranche verticale de l’aile, appelée profil. La déformation globale de l’aile correspond alors à un déplacement 2D de ce profil en translation (verticale et horizontale) et en rotation. Le comportement élastique de l’aile peut être modélisé par un ressort de compression et un ressort de torsion, attachés au profil à une extrémité et à un point fixe à l’autre. Ces ressorts s’opposent à la translation et à la rotation, comme illustré ci-dessous à gauche :

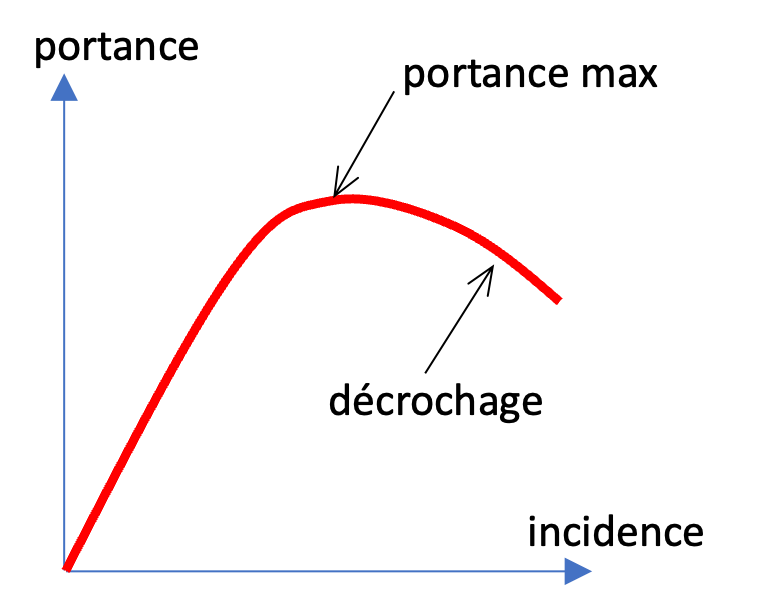Le profil est plongé dans un écoulement de fluide uniforme et permanent en amont. Sur la figure, l’avant du profil est la partie plus épaisse à gauche et l’arrière la partie plus fine à droite, l’avion se déplaçant vers la gauche à la rencontre de l’écoulement. Le point clé pour comprendre les instabilités naissant du couplage est lié au comportement du profil en fonction de l’angle d’incidence (angle formé par le profil et l’écoulement amont), comme montré sur la figure ci-dessus à droite. La force de portance est la force verticale exercée par le fluide sur le profil et provient d’une surpression sur la partie inférieure du profil et d’une dépression sur la partie supérieure. Pour des faibles incidences, les efforts de portance générés par le fluide croissent linéairement avec l’incidence, jusqu’à atteindre un maximum, puis la portance chute. C’est ce qu’on appelle le décrochage. Ce changement brutal est dû à la génération de larges tourbillons sur la partie supérieure de l’aile, qui réduisent la dépression. Le fonctionnement normal d’une aile correspond à une incidence faible.

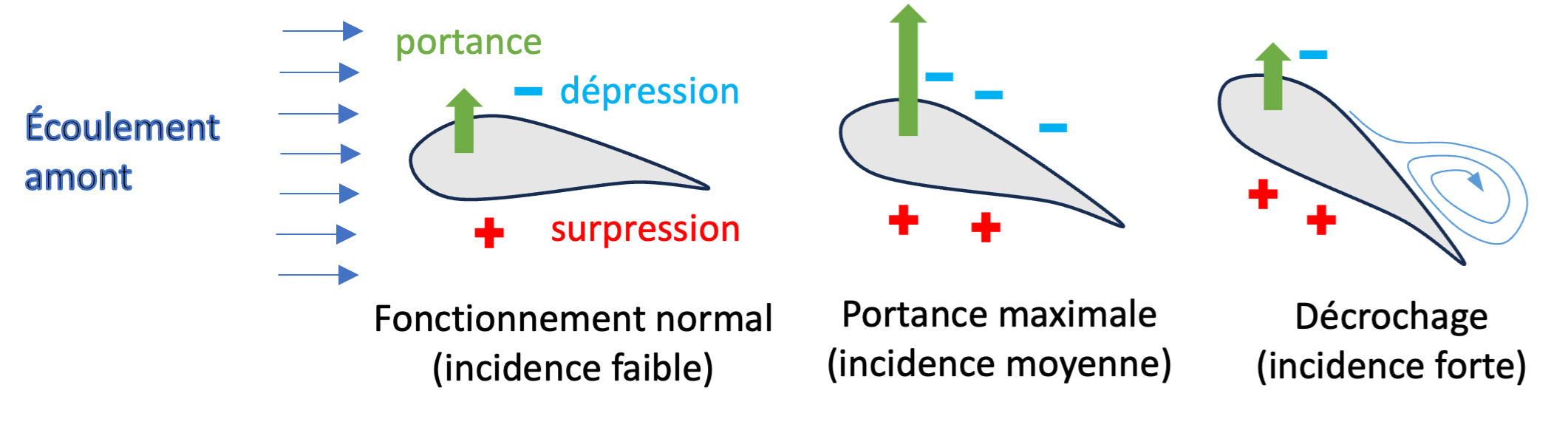
Examinons maintenant le résultat d’une simulation numérique réalisée pour cette configuration aéro-élastique. Pour cela, on a résolu les équations de Navier-Stokes pour le fluide, la seconde loi de Newton pour le profil attaché aux ressorts, ainsi que les deux conditions de couplage. On montre ci-dessous la composante horizontale du champ de vitesse du fluide, pour différents instants du mouvement. 

On a aussi représenté en rouge un ressort fixé au profil à une extrémité et à un point fixe de l’autre (le second ressort n’est pas montré pour des raisons de lisibilité).

Au premier instant (1), le profil est à faible incidence et l’effort de portance le fait progressivement monter. Dans le même temps, son incidence augmente car la force de portance se situe vers l’avant du profil et provoque sa rotation. Les différents ressorts s’allongent. On peut remarquer la présence de petits tourbillons du type Von Karman à l’arrière du profil. Arrivé à l’instant (2), on atteint la portance maximale, correspondant à une incidence et hauteur maximale. Le phénomène de décrochage survient alors, caractérisé par la génération d’un tourbillon plus important. La chute de portance provoque à l’instant (3) le basculement du profil, qui plonge à l’instant (4), tandis que les ressorts se rétractent et accélèrent le mouvement de retour. Le déplacement vers le bas se poursuit par inertie à incidence négative, jusqu’à ce que les ressorts exercent une force de rappel dans le sens opposé, à l’instant (5). Enfin, le profil reprend une incidence positive et un mouvement ascendant à l’instant (6). Le cycle est alors achevé et le mouvement se poursuit de façon périodique. Ce mouvement s’amorce par une instabilité aéro-élastique : la force exercée par le fluide induit un déplacement, qui va à son tour augmenter la force du fluide, qui provoque un déplacement plus important, etc. On parle de rétroaction positive, car les perturbations du fluide et de la structure s’amplifient l’une (?) l’autre (voir la page wikipedia sur la retro-action).

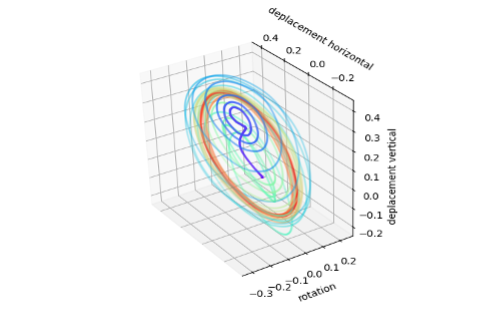
On représente sur la figure suivante le mouvement du profil tout au long de la simulation, selon trois axes représentant le déplacement horizontal, vertical et la rotation. La couleur correspond à l’évolution temporelle, du bleu (début) jusqu’au rouge (fin). On constate que pendant un premier intervalle de temps les oscillations s’amplifient, puis le mouvement tend vers un cycle limite (en rouge), correspondant aux phénomènes physiques périodiques illustrés précédemment.

Ce phénomène de flottement est bien entendu dangereux pour les avions car il provoque un risque de rupture des pièces par fatigue mécanique. Des études numériques et expérimentales très précises sont aujourd’hui menées pour empêcher l’apparition du flottement, en sélectionnant les propriétés structurales des ailes pour repousser le flottement en dehors des conditions de vol.

Retour à Tacoma

Les oscillations du pont de Tacoma sont dues en fait à cette même instabilité de type flottement. Le mécanisme est cependant plus complexe : la forme en H du tablier provoque la génération de tourbillons non symétriques dès l’avant de l’obstacle, qui se déplacent ensuite vers la partie arrière. Ces tourbillons en mouvement créent une rotation du tablier qui amplifie à son tour les tourbillons et les forces aérodynamiques, ces dernières augmentant la rotation, etc.

Le 7 novembre 1940, le pont va ainsi osciller pendant plus d’une heure selon un cycle limite, avant de s’effondrer suite à la rupture d’une pièce mécanique. Fort heureusement, aucune victime n’a été observée. L’analyse de cet accident a permis une avancée considérable dans l’étude de l’impact du vent sur les constructions humaines. Notamment, la forme en H du tablier a depuis été abandonnée au profit de formes plus aérodynamiques limitant le flottement, comme la forme trapézoïdale, moins génératrice de tourbillons. Au-delà de cette illustration, les propriétés aéro-élastiques sont aujourd’hui systématiquement étudiées par simulations numériques lors de la conception d’ouvrages d’art, comme les ponts (par exemple le viaduc de Millau) ou les gratte-ciels (le Burj Khalifa de Dubaï).