
Alan Turing, les motifs et les structures du vivant
Comment s’explique la formation de motifs lors du développement des organismes vivants ? En 1952, dans un article intitulé Les bases chimiques de la morphogenèse, Alan Turing présente un modèle mathématique très simple pour expliquer la morphogenèse. Suivant ce modèle, la conjonction de certaines réactions chimiques et de la diffusion moléculaire des réactifs conduit spontanément à une variation spatiale des concentrations des espèces chimiques, produisant des motifs en bandes ou en taches régulièrement espacées. De telles structures sont maintenant appelées « structures de réaction-diffusion » ou « structures de Turing ». Alan Turing suggère que ces processus purement physicochimiques pourraient être à la base de la morphogenèse animale et végétale en induisant le développement de structures répétées. Il prend pour exemples les motifs tachetés des guépards, le positionnement des tentacules de l’hydre ou des feuilles en rosette de l’aspérule, ainsi que la phase de développement de l’embryon appelée « gastrulation ».
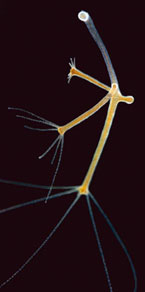

Hydres d’eau douce et aspérules odorantes. Alan Turing cite les exemples de l’hydre (un petit organisme vivant dans l’eau) et des feuilles d’aspérule. Ces deux organismes ont une forme assez similaire : les bras, les feuilles poussent en étoile autour du corps, de la tige. Un processus de développement analogue régirait leur croissance.
© Biosphoto / Joël Bricout (à gauche) – Biosphoto / Endress / Flora Press (à droite).
Un guépard. Son pelage tacheté et rayé est un objet d’étude de morphogénèse. Et si les motifs du pelage de ce guépard pouvaient se prédire ? se calculer ? C’est l’hypothèse qu’Alan Turing fait en travaillant sur les systèmes de substances chimiques qui réagissent et diffusent à travers un tissu (comme le pelage). En 1952, le mathématicien inaugure les débuts de la biologie théorique moderne.
L’implication du mécanisme de Turing dans la morphogenèse animale est un sujet encore débattu. Les motifs, comme ceux présents sur certains animaux, résultent d’une dynamique globale : on ne peut supprimer une tache sans les supprimer toutes. Leur période spatiale est entièrement déterminée par les paramètres de la dynamique. En revanche, le type de motif, en taches ou en bandes, dépend de la géométrie du système. Des simulations ont montré qu’un motif en taches se transforme en motif en bandes lorsque le rapport d’aspect entre la longueur et la largeur change. L’exemple couramment cité est celui des animaux tachetés, comme le guépard, qui présentent des taches sur le corps mais des rayures à l’extrémité de leur queue, plus étroite. Une difficulté de la validation est que le mécanisme de Turing peut n’être présent que pendant une courte phase du développement. Le fait que la distance entre les rayures augmente quand l’animal grandit, alors que le modèle de Turing la prédit constante, n’est pas un argument contraire suffisant.
Pour illustrer son modèle, Alan Turing cite deux exemples de morphogenèse : le positionnement des tentacules de l’hydre et celui, en rosette, des feuilles de l’aspérule. L’hydre est un animal aquatique pluricellulaire d’une dizaine de millimètres de long (du même embranchement que les méduses et les anémones de mer) capable de se régénérer après avoir été tronqué ou même passé à la moulinette et réduit à un amas informe de cellules. L’apparition des cinq à dix bras terminaux et leur positionnement en étoile régulière autour de la « bouche » de l’animal semblent régis par un mécanisme de Turing au niveau moléculaire. Un processus analogue expliquerait le bourgeonnement en rosette des feuilles de l’aspérule à un niveau donné de la tige. Turing argumente que la « bouche » de l’hydre et la périphérie de la tige de la plante peuvent être assimilées de par leur géométrie au cas de l’anneau de cellules qu’il a déjà résolu mathématiquement. La résolution du modèle permet ainsi de déterminer le nombre de tentacules ou de feuilles produites.
Un article fondateur
Alan Turing ne prétend pas qu’il s’agit du seul mécanisme possible de morphogenèse, ni même qu’il est effectivement à l’œuvre dans tel ou tel système vivant – il est conscient du manque de preuves expérimentales. Son but est davantage de proposer un mécanisme plausible et de montrer tout ce qu’il permet déjà d’expliquer, malgré sa simplicité. Il souligne que le modèle est une « simplification » et une « idéalisation » et par conséquent, une « falsification », mais il fait la pétition de principe que les quelques mécanismes retenus sont effectivement les mécanismes dominants. Notre propos n’est pas ici de valider l’implication des structures de Turing dans la morphogenèse biologique, mais plutôt de présenter les apports tout autant techniques que conceptuels de son approche, en soulignant sa modernité.
Expliquer la formation de motifs
Alan Turing souligne d’entrée le défi majeur : comment passe-t-on d’un embryon au départ parfaitement symétrique, une sphère, à un organisme structuré ? Il ramène ce problème à celui de la formation de motifs à partir d’un état homogène. Ce phénomène a déjà un nom : on parle de « brisure spontanée de symétrie ». Pourquoi ce terme, alors que les structures de Turing présentent de remarquables symétries, en l’occurrence une « périodicité spatiale des motifs », en bandes ou en taches suivant la géométrie du système (suivant la forme de l’animal par exemple) ? C’est par rapport à la symétrie complète de l’état homogène de départ qu’il y a brisure de symétrie. Mathématiquement, cela se reflète dans le fait que la solution de l’équation d’évolution présente moins de symétries que l’équation elle-même. Alan Turing donne tout de suite l’explication de base : les différentes perturbations que peut subir l’état homogène vont évoluer différemment. Certaines vont être amorties, d’autres amplifiées : ces dernières présentent des caractéristiques particulières qui se refléteront dans la solution, alors que les premières n’auront aucun effet. Ceci n’est rien d’autre qu’un phénomène de résonance, bien connu dans l’étude des pendules et autres oscillateurs. Une conséquence notable en est que la perturbation ne détermine pas les caractéristiques des motifs mais seulement la possibilité de leur émergence. L’idée est remarquable : suivant le modèle de Turing, la formation des motifs est spontanée, elle ne nécessite ni patron préalable ni prescription extérieure.
Une conjonction de réactions chimiques et de diffusion
La dynamique qu’Alan Turing explicite dans son modèle résulte du couplage entre des réactions chimiques et la diffusion des réactifs, dans un système alimenté en continu. Les structures de Turing correspondent aux variations spatialement périodiques des concentrations des espèces chimiques. L’effet de la diffusion moléculaire est en général d’homogénéiser un mélange d’espèces chimiques. Pour observer des variations spatiales de concentrations, il faut donc que d’autres mécanismes entrent en jeu. Alan Turing propose un scénario impliquant deux espèces, qu’il appelle « morphogènes » et la conjonction des propriétés suivantes :
- l’espèce A active sa propre production ;
- l’espèce A active aussi la production de la seconde espèce B ;
- l’espèce B inhibe la production de A ;
- B diffuse plus vite que A.
Il suffit alors qu’une petite fluctuation locale induise un léger excès de l’activateur A pour que la production de A et de B s’accélère à cet endroit. L’excès de B, diffusant plus vite que l’excès de A, crée une couronne inhibitrice autour du point initial, isolant le pic de A par une zone plus riche en B. Cette explication intuitive et locale doit être complétée par une vision plus globale. À une certaine distance de la première fluctuation, une autre peut se développer de façon analogue et créer un pic de A et ainsi de suite. Ces pics d’activateur découlent de l’amplification sélective des fluctuations, infimes mais innombrables, qui affectent spontanément l’état de mélange homogène. La répartition dynamiquement la plus stable de ces pics forme un motif périodique, comme les taches que l’on peut observer sur le guépard. Alan Turing parle d’« ondes stationnaires » pour désigner un tel motif, mais le terme ne doit pas prêter à confusion : la dynamique est très différente des équations d’onde décrivant la propagation du son ou de la lumière. Pour rendre compte de ces mécanismes moléculaires, Alan Turing considère un modèle macroscopique en termes de concentrations des espèces chimiques, sans jamais oublier qu’il s’agit d’une approximation que la réalité déborde. En termes mathématiques, l’évolution du système est décrite par un système d’équations différentielles (dans le cas discret où le système est représenté comme un ensemble fini de cellules et leurs concentrations respectives en espèces chimiques) ou par une équation aux dérivées partielles (dans le cas continu où le système est représenté à l’aide de champs de concentration, c’est-à-dire des fonctions continues de l’espace et du temps).
L’effet de la diffusion sur la concentration d’une espèce chimique est décrit par une équation de diffusion. Cette équation aux dérivées partielles rend compte de la diffusion des molécules depuis les régions de grande concentration vers les régions de faible concentration, avec un courant proportionnel au gradient de concentration. Dans les systèmes de réaction-diffusion, il s’ajoute un terme de réaction chimique, purement local. De telles équations sont utilisées pour modéliser des phénomènes naturels les plus divers, allant de la propagation d’un front de combustion ou d’une épidémie aux ondes spirales observées dans des milieux excitables, tel le tissu cardiaque ou les réseaux de neurones. Les mêmes méthodes de résolution s’appliquent.
Prédiction de la période des motifs
Alan Turing se concentre sur le moment où l’état homogène laisse place à un état structuré : c’est le moment où le mécanisme symétrie est à l’œuvre. Ce qui se passe est bien décrit par une équation d’évolution linéarisée. Une méthode de résolution systématique consiste à chercher la solution comme une superposition de modes sinusoïdaux. Le caractère linéaire de la dynamique approchée permet de considérer séparément le devenir de chaque mode. Alan Turing met en évidence des modes dits « instables » car leur amplitude augmente sous l’effet de la dynamique. Il établit la condition d’instabilité en fonction des paramètres du modèle, en particulier le rapport des coefficients de diffusion des deux espèces en présence. Il montre que plusieurs régimes sont possibles : des motifs périodiques stationnaires mais aussi des structures se propageant à vitesse constante. Cette analyse linéaire de stabilité n’est valable qu’assez près de l’état d’équilibre homogène. La période spatiale du motif est simplement celle du motif le plus instable. Alan Turing montre ainsi que cette période est intrinsèque, contrôlée par la dynamique et non due à une hétérogénéité préalable du milieu, à la géométrie ou aux conditions initiales. Il faut souligner que l’échelle spatiale des motifs est sans commune mesure avec les échelles moléculaires des processus sous-jacents, montrant le caractère émergent de leur formation. Il n’y a pas de traitement systématique de l’équation d’évolution non-linéaire pour laquelle Alan Turing recommande le recours à une résolution numérique, avec la restriction que seule une étude au cas par cas est alors possible. En présence de plusieurs modes instables, le nombre de bandes ou de taches observées dans le motif peut varier de quelques unités. On observe par exemple une variation du nombre de tentacules chez l’hydre et du nombre de feuilles dans une rosette chez l’aspérule. Alan Turing termine son article par extension à la sphère en décomposant la solution cherchée sur une base d’harmoniques sphériques. L’application qui le motive est l’étape de l’embryogenèse appelée « gastrulation », durant laquelle on observe la première invagination de l’embryon jusque-là sphérique.
Une validation expérimentale délicate mais avérée

Structures de Turing observées dans un réacteur chimique. Ces deux motifs sont les premières observations scientifiques réalisées en 1990 grâce à un réacteur chimique, de la théorie imaginée par Alan Turing. Même s’il avait clairement déroulé sa démarche en 1952, il a fallu réunir de nombreux paramètres pour valider sa théorie par l’expérience.
© Patrick De Kepper, Centre de recherche Paul-Pascal (CNRS).
Il a fallu attendre quarante ans et un concours de circonstances pour obtenir la première mise en évidence expérimentale d’une « structure de Turing », c’est-à-dire d’un motif en bandes ou en taches régulièrement espacées, observé dans un système alimenté en continu, et résultant du mécanisme de réaction-diffusion proposé par Turing. En effet, les conditions expérimentales favorables sont difficiles à réunir. Pour qu’un mélange uniforme d’espèces chimiques se déstabilise sous l’effet des réactions et de la diffusion moléculaire des réactifs, il doit contenir une espèce autoactivatrice A, qui active aussi la production d’une seconde espèce B inhibitrice, et il faut que B diffuse plus vite que A. Cette seconde condition n’est pas souvent réalisée : la molécule B doit être beaucoup plus grosse que A. Ici, cela se produit car B forme un complexe chimique avec une molécule d’amidon, grosse molécule qui a été choisie au départ pour faciliter la visualisation. De plus, les réactions sont réalisées dans un gel, afin d’éviter que le mélange redevienne homogène.
Pour aller plus loin : voir les articles de P. de Kepper et E. Dulos mentionnés dans le Savoir +.
Il a fallu quarante ans avant que les premières structures de Turing soient mises en évidence expérimentalement. Il faut en effet des situations assez particulières où le coefficient de diffusion de l’espèce inhibitrice est beaucoup plus grand que celui de l’espèce activatrice. Il est possible que le mécanisme proposé par Alan Turing ne fournisse qu’un principe directeur de la formation des motifs observés chez les êtres vivants et que d’autres mécanismes plus fins et plus spécifiques s’y ajoutent. En effet, la similitude des motifs observés ne fournit pas la preuve que le mécanisme proposé par Alan Turing est réellement à l’œuvre. Ce piège de l’analogie se rencontre par exemple avec la structure en bandes d’un embryon de drosophile, tout à fait similaire à une structure de Turing mais où, comme l’a montré John Maynard Smith, chaque bande est en fait contrôlée individuellement par un mélange de morphogènes qui lui est spécifique. Pour obtenir des arguments supplémentaires en faveur d’un mécanisme de Turing ou pour le rejeter, on étudie les défauts et la réponse à des perturbations, par exemple la régénération ou non des motifs lors de la cicatrisation après une blessure. Cette étude permet de mieux révéler les mécanismes à l’œuvre et de préciser le niveau auquel ils entrent en jeu lors de l’embryogenèse ou bien en continu lors de la croissance de l’animal.
Des perspectives encore prometteuses aujourd’hui
L’article d’Alan Turing, très riche, est cependant écrit avec un grand effort pour rendre accessibles les aspects techniques, tant mathématiques que biologiques. Alan Turing y annonce une série de résultats, à paraître dans un article ultérieur… sa mort prématurée nous en a privés. Son approche est méthodologiquement exemplaire : le modèle qu’il propose montre la richesse de structures qu’on peut expliquer en n’invoquant qu’un ensemble minimal de mécanismes uniquement physicochimiques, sans avoir besoin d’arguments ou d’ingrédients spécifiques. En indiquant que les gènes contrôlent les vitesses des réactions impliquées, il fait un pas majeur dans l’explication du lien entre le génotype et les traits observés, le phénotype. Alan Turing mentionne la contribution mécanique à l’évolution du système, en particulier des forces et contraintes élastiques : il anticipe ainsi tout un champ de recherches actuel, étudiant le rôle des couplages mécanochimiques dans les processus intracellulaires ou cellulaires. Alan Turing mentionne également, sans la traiter, la difficulté liée au fait que le substrat, ici un embryon en train de se développer, n’a pas une géométrie fixée mais une géométrie qui évolue avec le temps. Ce n’est que très récemment que des chercheurs tels Jean-Louis Giavitto (un des auteurs du numéro de la revue DocSciences où cet article est paru) et ses collaborateurs ont développé le concept de « système dynamique à structure dynamique » pour envisager la formation de motifs dans un système lui-même en évolution. Et l’extension du modèle de Turing à des géométries déjà structurées, réseaux ou substrats lacunaires, commence seulement à être envisagée.
- Bourgine P., Lesne A., Morphogenèse. L’Origine des formes, coll. « Échelles », Belin, 2006.
- De Kepper P. & Dulos E., « Chimie des formes et motifs de pelage », Pour la Science, Dossier n° 44, 2004.
- De Kepper P., conférence en ligne, Morphogénèses chimiques : les réactions créatrices de rythmes et de formes, août 2000.
- Koch A.-J. & Meinhardt H., « Biological pattern formation », Reviews of Modern Physics, n° 66, p. 1481-1507, 1994.
- Maynard Smith J., La Construction du vivant, Cassini, 2001.
- Meinhardt H., The Algorithmic beauty of sea shells, Springer, 1995.
- Murray J.-D., Mathematical biology, Springer (2005).
Cet article est paru dans la revue DocSciences n°14 Alan Turing : La pensée informatique, éditée par le CRDP de l’Académie de Versailles en partenariat avec Inria.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Annick Lesne