
Au pays des illuminés du nombre Pi
Une première version de cet article est parue dans la rubrique « Logique et calcul » de la revue Pour la Science, n°463, en mai 2016.
Le nombre π a beaucoup d’amis. Il serait parfois souhaitable qu’il en ait moins, car la passion pour le nombre d’Archimède suscite d’étranges et invraisemblables histoires. Plus que n’importe quel nombre, π intéresse : on travaille et on s’amuse avec lui, et parfois… on délire.
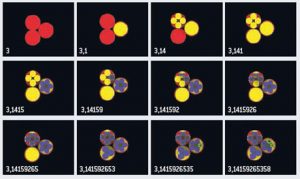
Francesco De Comité, du laboratoire CRISTAL de l’université de Lille 1, a conçu et réalisé une sculpture virtuelle originale de π. Pour la construire, on part d’un disque. Le premier chiffre de π est un 3, aussi place-t-on à l’intérieur 3 disques de même rayon occupant le plus de place possible dans le premier disque. Cela détermine 3 nouveaux disques où l’on inscrira, selon le même principe, les trois décimales suivantes : 1, 4 et 1. Pour les 1, on place un disque concentrique un peu plus petit que le disque d’accueil ; pour les 0, on place 10 disques. Les disques ainsi créés (pris dans l’ordre de leur création) permettent d’inscrire de nouvelles décimales, cela jusqu’à l’infini (à mesure qu’on utilise certains disques en les remplissant, d’autres sont créés). En utilisant des cylindres de plus en plus hauts dont les bases sont les disques ainsi obtenus, on rend visibles ces disques et on obtient une sculpture des décimales de π.

Dans le schéma explicatif ci-dessous, on a utilisé la couleur rouge pour les trois premiers disques. On remplit ces disques par des disques jaunes. Quand il n’y a plus de disques rouges disponibles, on remplit les disques jaunes par des disques violets. Quand les disques jaunes sont épuisés, on remplit les disques violets par des disques verts, etc.
La date du 14 mars, que l’on écrit souvent 3-14 dans le monde anglo-saxon, a été déclarée journée de π. Diverses manifestations s’y déroulent, en particulier à l’université de Marseille depuis trois ans.
À l’occasion de cette journée, l’éditeur de jeux et casse-tête Brainfreeze Puzzles a créé des sudokus originaux et intéressants, disponibles pour tous et qui ont été soumis aux élèves de nombreuses classes dans le monde. En voici deux. Attention, les règles liées à π ne sont pas les règles habituelles.
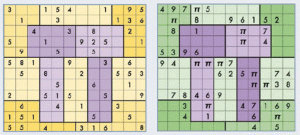
Dans le sudoku de gauche, il faut que chaque ligne, chaque colonne et chaque zone dessinée contienne les 12 premiers chiffres de π, qui sont 3 1 4 1 5 9 2 6 5 3 5 8. Il y aura donc deux fois le 1, une fois le 2, deux fois le 3, une fois le 4, trois fois le 5, une fois le 6, pas de 7, une fois le 8, une fois le 9.
Pour le sudoku de droite, chaque ligne, chaque colonne et chaque zone dessinée doit contenir chacun des chiffres 1, 2, …, 9 une fois exactement et le symbole π trois fois.
Certains lui préfèrent le « nombre d’or » Φ, égal à (1 + √5)/2. Dans les librairies pour le grand public, on trouve plus de publications consacrées à Φ que dédiées à π, mais c’est sans doute parce qu’il est plus élémentaire et qu’il est associé à certaines croyances numérologiques. On trouve d’ailleurs aussi plus de livres d’ésotérisme que de science dans les rayons de ces mêmes librairies : certains de ces magasins vendent du matériel de haute technologie (appareils photo, télévisions, téléphones, ordinateurs, etc.) qui naissent des progrès de la science et, étrangement, orientent leurs clients vers la littérature spiritualiste, occultiste ou superstitieuse…
Pour les scientifiques, cependant, il n’y a aucun doute : π est le roi des nombres, celui qui réunit le plus de mystères et d’étrangetés, celui qui a la plus grande importance mathématique. Il incite aux rêves et parfois engendre la folie, comme celle d’en calculer de nombreuses décimales : aujourd’hui, on connaît 13 300 milliards de chiffres de π. Si on les imprimait, cela donnerait l’équivalent de dix millions d’ouvrages assez gros. Aucun œil humain n’a bien sûr parcouru ces chiffres calculés, qui n’existent que dans la mémoire des ordinateurs !
On remarquera que Φ n’est pas connu de tout le monde, alors que π, lui, s’apprend à l’école primaire et ne s’oublie jamais. Le nombre Φ est algébrique : il est une solution de l’équation simple x2 = x + 1, alors que π est « transcendant ». Ce résultat démontré il y a plus d’un siècle par Ferdinand von Lindemann signifie que π n’est la solution d’aucune équation polynomiale à coefficients entiers (comme celle citée pour Φ).
Calculer Φ revient à calculer la racine carrée de 5, ce qui, par tâtonnements, est facile, alors qu’aucune méthode aussi naturelle, rapide et simple n’est disponible pour π. Le nombre Φ est le préféré des snobs et des naïfs qui pensent qu’il donne le secret de la beauté, alors que c’est plus que douteux (voir le livre de Marguerite Neveux dans la bibliographie). Au contraire, le nombre π s’impose, qu’on ait envie de le connaître ou pas. Il est dans votre poche, où le diamètre et la circonférence des pièces de monnaie sont liés par π. Il est dans le volume de la Terre et sa surface, que l’on calcule à partir de son rayon et de π. Il est dans la longueur du trajet parcouru par votre voiture, égale à π fois le nombre de tours fait par une roue multiplié par son diamètre. Il est dans les lois de probabilités. Il est partout en physique et bien d’autres sciences.
Du fait de son importance incontestable, certains veulent s’approprier π et en apprennent par cœur les décimales. Ce sport un peu fou est maintenant coordonné par un site internet qui, après avoir fixé clairement les règles du jeu, maintient à jour une liste « officielle » des records successifs.
Les règles indiquent qu’on ne compte que les chiffres décimaux après le « 3, ». Aucune erreur n’est autorisée lors de l’énumération de ces décimales, qui doit s’effectuer dans l’ordre et en public. Deux témoins non liés au « récitant » doivent certifier l’exploit. Lorsque le nombre de décimales dépasse 10 000, un troisième témoin officiel (notaire, huissier, etc.) doit assister à la performance, puis remplir et signer un formulaire.
Le record : plus de 70 000 décimales récitées
Aujourd’hui, le record officiel est détenu par l’Indien Suresh Kumar Sharma qui, le 21 octobre 2015, a récité 70 030 décimales de π en 17 heures et 14 minutes. Il a ainsi battu de peu le record précédent de l’étudiant indien de 21 ans Rajveer Meena, qui avait récité, les yeux bandés pour mieux se concentrer, 70 000 décimales de π. La performance s’était déroulée le 21 mars 2015 et avait duré 9 heures et 27 minutes, ce qui correspond à 2 chiffres par seconde, bien plus vite que le détenteur actuel du record. Ce record a été validé par le très exigeant Livre Guinness des records.
Un peu avant encore, le record était détenu par un Chinois, Chao Lu, qui avait récité 67 890 décimales en un peu plus de 24 heures (moins d’un chiffre par seconde). Dans un entretien, il précisait que le travail de mémorisation lui avait demandé une année. Il expliquait aussi qu’il connaissait 100 000 décimales de π, mais que lors de l’épreuve, il avait malencontreusement dit « 5 » pour le 67 891e chiffre, alors qu’il aurait dû dire « 0 ». C’était sa seule erreur, mais elle a rendu impossible la validation des 100 000 décimales.
Quelques années auparavant, en 2006, le Japonais Akira Haraguchi, alors âgé de 59 ans, avait lui aussi récité 100 000 décimales de π. Malheureusement, les informations sur son exploit n’ont pas été jugées assez précises et sûres pour que son record soit reconnu.
Lors d’un entretien donné à un journaliste du Guardian en mars 2015, il affirmait : « Mon affection et mon respect pour π n’ont jamais cessé depuis 2006. En 2010, j’ai posté une vidéo dans laquelle je récite 101 031 décimales de π. Depuis, j’ai encore progressé et je peux en réciter 111 700. Chaque jour depuis 2006, je récite 15 000 décimales, ce qui me demande environ une heure. Pour moi, réciter π, c’est comme chanter un mantra bouddhiste et méditer. J’essaie en ce moment d’aller plus loin et de réciter 25 000 chiffres chaque jour, ce qui m’occupe environ trois heures. »
Des histoires « chiffrées »
Akira Haraguchi a expliqué la philosophie qui l’encourage à poursuivre ses efforts : « Toutes les choses de ce monde, nous-mêmes inclus, sont des agrégats d’atomes, qui sont faits d’électrons qui tournent. La Terre tourne, la Galaxie aussi, l’Univers aussi. Autrement dit, je crois que la rotation est la vérité absolue. Lorsque je pense à π, je vis en harmonie avec cette vérité. »
Le système mnémotechnique d’Akira Haraguchi consiste à associer un chiffre à chaque son utilisé par la langue japonaise. Mémoriser π revient alors pour lui à apprendre des histoires qu’il crée en suivant les décimales de π. Ce sont elles qu’il retient mot à mot et qu’il traduit en liste de chiffres au moment de ses récitations quotidiennes. Il précise : « J’ai créé environ 800 histoires, principalement au sujet d’animaux et de plantes. Pour les 100 premiers chiffres de π, j’ai fabriqué une histoire dont voici le début : ‘‘Bien, moi cet être fragile qui a quitté sa maison pour trouver la paix de l’esprit, je vais mourir dans un coin noir ; c’est facile de mourir, mais je reste optimiste…’’ »
Réciter 200 000 décimales ?
Même si des critères sévères de validation empêchent la reconnaissance des records de Akira Haraguchi jusqu’à 100 000, il ne semble plus faire de doute que mémoriser 100 000 décimales de π est possible à un être humain décidé. Pourra-t-on aller plus loin et, par exemple, atteindre 200 000 ? Cela semble douteux, mais qui sait ? Lorsque le nombre de 50 000 fut atteint, de nombreux spécialistes jugeaient impossible de doubler le record.
Par imagerie cérébrale, le neurobiologiste Amir Raz, de l’université Columbia aux États-Unis, et ses collègues ont observé le cerveau d’un sujet apprenant et récitant des décimales de π. Le sujet de leur étude, un étudiant de 22 ans, utilisait le procédé mnémotechnique antique des loci pour mémoriser les chiffres. Il consiste à imaginer qu’on parcourt un édifice réel dont on a associé les différentes pièces ou éléments de décor aux choses que l’on doit fixer dans sa mémoire.
Outre des précisions sur les parties du cerveau sollicitées par ce type d’exercices, l’une des conclusions de l’article des neurobiologistes est que les exploits de ce genre tiennent bien plus à un entraînement prolongé et la maîtrise de bonnes méthodes mnémotechniques qu’à la possession d’un don particulier.
L’histoire la plus extraordinaire à propos de la mémorisation des décimales de π est incontestablement celle de Andriy Slyusarchuk, un étonnant personnage né en Ukraine en 1971 et surnommé par la presse de son pays Docteur Pi. Il se présentait comme diplômé en médecine, psychiatre, neurochirurgien, psychothérapeute, joueur d’échec de haut niveau et capable d’exploits de calcul mental et de mémorisation hors du commun. Son talent, qu’on peut comparer à celui du Français Christophe Rocancourt surnommé « l’escroc des stars », le conduisit à être accueilli par diverses universités et institutions de recherche, à recevoir des prix pour ses travaux scientifiques et ses actions, à exercer comme chirurgien, à être invité de nombreuses fois à la télévision, et à vendre très chers des médicaments à des malades en fin de vie. Il occupa même des fonctions dans un ministère et reçut le soutien de deux présidents ukrainiens, Viktor Iouchtchenko et Viktor Ianoukovytch.
Docteur Pi, l’escroc aux 300 millions de décimales
Concernant π, à l’occasion de démonstrations en public, il réussit à convaincre un certain nombre d’observateurs qu’il en connaissait 30 millions de décimales. Il prétendit même plus tard en connaître 300 millions. Bien sûr, il ne les récitait pas, mais en indiquait des tranches en réponse à des questions qu’on lui posait. Notons qu’à raison d’une décimale par seconde sans jamais s’arrêter, il faudrait 9,5 ans pour énumérer les 300 millions de décimales prétendument connues par le Docteur Pi. C’est impossible : pour apprendre ces mêmes décimales en y consacrant tout son temps nuit et jour, à raison d’une décimale apprise par seconde, il faut là encore 9,5 ans de travail. Comment a-t-on pu le croire ?
Ses records n’ont pas été validés et, bien que n’ayant jamais été pris en flagrant délit de tricherie, certains soupçonnaient qu’un complice, à l’aide d’un appareil caché dans son oreille, lui soufflait les réponses.
Après des années de succès divers durant lesquelles il s’enrichit, en particulier grâce à de prétendus remèdes miraculeux mis au point par ses soins, les choses se mirent à mal tourner. On découvrit qu’il n’avait pas les diplômes qu’il prétendait posséder. Plus tard, un informaticien avoua à la presse qu’il avait créé des programmes pour aider Andriy Slyusarchuk dans ses exploits concernant π et qu’il l’avait aussi assisté pour composer des articles scientifiques en plagiant des articles déjà publiés. Les enquêtes déclenchées alors aboutirent le 14 février 2014 à sa condamnation à 8 ans de prison pour une série de faits, certains graves : faux et usages de faux, pratique illégale de la médecine, meurtre par négligence (certaines de ses interventions chirurgicales furent catastrophiques), etc. Aux dernières nouvelles, il a tenté de se suicider en prison.
Le nombre π peut se calculer de mille façons différentes par des formules de toutes sortes : limites de suites particulières (qui par exemple convergent vers la longueur du périmètre d’un cercle de diamètre 1 : c’est l’idée de la méthode d’Archimède), intégrales (donnant l’aire d’un disque de rayon 1), séries infinies, produits infinis, etc. L’article Le nombre Pi est partout présente une variété de méthodes nouvelles ou inattendues de calcul de π.
Toutes ces formules et méthodes conduisent au même nombre exactement, et cette affirmation résulte dans chaque cas particulier d’une démonstration mathématique incontestable. Le nombre π est une sorte d’attracteur mathématique qui aspire des nombres provenant d’origines diverses et qui, au travers de formules différentes, s’accordent comme par miracle.
Si les démonstrations mathématiques indiquant qu’on tombe bien sur un seul et même nombre ne vous satisfont pas, vous pouvez contrôler l’accord des formules à l’aide de calculs par ordinateur. En tirant de chacune des définitions une procédure de calcul et un programme, vous obtiendrez des décimales correspondant aux différentes formules donnant π. Vous comparerez les résultats et découvrirez expérimentalement l’unicité du nombre calculé. Aujourd’hui, personne ne peut donc douter que π = 3,1415926535 8979323846 2643383279 5028841971 6939937510… (pour d’autres décimales, voir par exemple le lien).
Les obstinés simplificateurs de π
Cependant, π reste compliqué, et l’être humain cherche à simplifier tout ce qui peut l’être et rêve de formules élémentaires. Poussé à l’extrême, ce désir conduit à une forme de folie. Pour se débarrasser du mystère de π et de la gêne ressentie face à la complexité des mathématiques qui lui sont attachées, certains se persuadent que π est bien plus simple que tout ce qu’on a cru jusqu’à maintenant.

Les simplificateurs de π désaprouvent le consensus des mathématiciens sur la valeur de la constante π. Cette discordance diminue leur crédibilité. Dans l’article est mentionné André Aigoin, qui rejette absolument le π des mathématiciens (qu’il dénomme le « π officiel »). Pour lui, π vaut 4√(2143/22) = 3,14159265258264612521…
Cette valeur n’est pas compatible avec celle publiée par l’Indien Sarva Jagannadha Reddy qui, dans de nombreux articles et deux livres, soutient que l’authentique valeur de π est le nombre : (14 – √2)/4 = 3,1464466094…
Aucune de ces deux valeurs n’est conforme avec celle proposée par Mohammadreza Mehdinia, qui vit en Suède et a publié (en plusieurs langues) l’ouvrage The correct value for π (qu’on trouve gratuitement en PDF), dans lequel il défend que la bonne valeur de π est tout simplement 3,125 = 25/8 (voir aussi le lien).
Pendant un temps, 500 000 couronnes suédoises étaient offertes à qui trouverait une erreur dans le livre de Mehdinia, mais depuis peu l’offre a été retirée. Quelqu’un aurait-il gagné ? D’autres valeurs de π avaient déjà été proposées plus tôt dans l’histoire, dont l’une, la valeur 3,2, avait failli être imposée par une loi de l’État d’Indiana, aux États-Unis.
Les mathématiciens « officiels » ont au moins un avantage sur leurs contradicteurs : ils sont d’accord entre eux !
Cette volonté simplificatrice s’est longtemps exprimée sous forme géométrique. C’était l’époque des « quadrateurs du cercle ». Avec une règle (non graduée) et un compas, on tentait de construire un carré de même aire qu’un cercle donné. La nature transcendante de π a pour conséquence que c’est impossible : toute prétendue solution au problème de la quadrature du cercle est nécessairement fausse. Aujourd’hui encore, certains passionnés de géométrie s’attaquent en vain au problème de la quadrature, mais ils sont déconsidérés et plus personne ne leur prête attention.
Il existe cependant une forme nouvelle et algébrique du désir de ne plus subir la complexité intrinsèque de π. Je vais mentionner plusieurs cas remarquables des effets de cette volonté simplificatrice en passant rapidement sur les deux premiers largement connus aujourd’hui.
Dans la Bible, on trouve l’affirmation indirecte que π = 3. C’est une belle simplification, mais il ne s’agit pas d’un texte mathématique et il n’est pas certain que le passage qu’on interprète de cette façon signifiait vraiment pour ses auteurs que π = 3.
Un formidable simplificateur de π fut l’Américain Edward Johnson Goodwin, qui réussit presque à faire adopter une loi pour imposer ses « découvertes ». En 1897, il mena une série de raisonnements et de calculs dont l’un donnait π = 3,2 = 16/5. Il proposa à l’État d’Indiana d’en faire une constante officielle pour simplifier la vie de tous. L’intention était louable. Heureusement, il échoua (voir ici).
Une formule (trop) simple du Midi
Après la parution de mon livre sur π en 1997, j’ai reçu, étalées sur une période d’un an, une dizaine de lettres d’André Aigoin, un amateur de mathématiques du midi de la France qui proposait ceci :
π = 4√(2143/22) = 3,1415926 5258…
L’approximation est intéressante et peut certainement servir à des usages pratiques, mais le nombre proposé n’est pas π et les arguments de mon correspondant ne convaincront aucun mathématicien.
Je tentais en vain de le ramener à la raison : son expression faisait de π un nombre algébrique, ce qui contredit le résultat de von Lindemann. La conviction de ce correspondant était très forte et le conduisait dans ses lettres à exprimer de l’hostilité à l’égard de l’autre π (celui de tout le monde), qu’il appelait avec insistance et hargne le « π officiel » ou même l’« usurpateur ». Ce simplificateur de π, à ma connaissance, ne parvint jamais à publier ses élucubrations qui sont donc restées dans ses dossiers et les miens.
Les temps ont changé et, grâce à Internet et à la multiplication récente de pseudo-journaux scientifiques, toute idée, aussi farfelue soit-elle, peut aujourd’hui trouver sa place sur la Toile et même comme article dans une revue prétendument scientifique. Toute folie est en mesure de se déclarer « validée par la communauté académique », ce qui trompera les journalistes peu attentifs et les amateurs mal informés.
J’ai pris conscience de cette nouvelle situation en recevant, il y a quelques mois, un livre (en version pdf) que m’a fait parvenir son auteur. Jamais un simplificateur de π n’avait aussi bien réussi que ce Sarva Jagannadha Reddy, qui se présente comme un retired zoology lecturer habitant à Tirupati en Inde. Son livre, écrit en anglais, est intitulé The Gayatri Pi value.
Des revues prédatrices qui publient n’importe quoi, si l’on paye
Que l’on puisse publier n’importe quoi n’est pas une nouveauté ; lui-même avait auparavant publié un ouvrage donnant sa version simplifiée de π, et bien d’autres farfelus ont publié à compte d’auteur des solutions du problème de la quadrature du cercle. Ce qui m’a étonné est que le livre reçu est composé de la reproduction de 15 articles dont la plupart avaient auparavant été publiés dans des revues scientifiques d’apparence académique. Voici quelques-uns des titres de ces revues : International Journal of Mathematics and Statistics Invention, International Journal of Engineering Inventions, International Journal of Latest Trends in Engineering and Technology. On peut rechercher sur Internet les sites de ces revues et contrôler qu’effectivement les articles reproduits dans le livre y ont bien été publiés.
Je ne connaissais aucune de ces revues et, sans avoir mené une enquête détaillée, je pense qu’elles appartiennent toutes à la catégorie des nombreuses récentes revues où l’auteur paye pour être publié et où le contrôle scientifique par une expertise demandée à des personnalités compétentes est léger, simulé ou totalement inexistant. Ces fausses revues, parfois qualifiées de prédatrices, sont une plaie pour la communauté scientifique. Comme le montre l’exemple de Sarva Jagannadha Reddy, on peut y publier les plus grosses âneries en contradiction totale avec l’état des connaissances sans être soumis à aucun contrôle véritable ; il suffit de payer. Une liste des éditeurs de ces revues faussement scientifiques est maintenue à jour.
Les articles reproduits dans le livre de Sarva Jagannadha Reddy proposent tous des arguments conduisant à π = (14 – √2)/4 = 3,1464466094…, ce qui est nettement moins bon que l’approximation de mon correspondant français. La formule fait à nouveau de π un nombre algébrique… ce qui, si les preuves données étaient correctes, constituerait une révolution mathématique sans précédent, puisqu’on aurait une contradiction au cœur même de la théorie des nombres !
Pour l’auteur, la valeur de π admise par le reste du monde provient d’erreurs de raisonnements qu’il analyse. Ce faisant, il montre qu’il n’a rien compris et n’a même pas atteint le niveau de compréhension en matière de théorie des nombres qu’avait Archimède il y a 2 000 ans, niveau qui depuis est devenu plus précis encore, quand le concept de nombre réel a été mieux maîtrisé. Je ne discuterai pas ici des erreurs de Sarva Jagannadha Reddy, d’autres l’ont fait. Ses articles sont des non-sens absolus.
Simplifier π est un rêve, et c’était sous une forme géométrique celui de tous les quadrateurs du cercle. Le fait que le nombre π soit transcendant signifie qu’il ne pourra jamais se simplifier beaucoup et que les amateurs qui veulent s’affranchir de la réalité du monde délicat des mathématiques perdent leur temps. Le nombre π a beaucoup d’amis, et c’est parfois un grand malheur.
Et il est affligeant que se soit développée une littérature d’apparence scientifique, prête à publier n’importe quel article pourvu qu’on paye. Elle nuit au bon fonctionnement de la science. Cette littérature donne l’illusion à certains de mener un travail contrôlé et reconnu, ce qui n’est pas vrai. Cela rend plus difficile à l’amateur sincère et curieux de faire le tri entre la science et le simulacre de la science.
Quelques références vous sont proposées pour en savoir plus sur le nombre π.
- Wikipedia, Andriy Slyusarchuk, page consultée en février 2016.
- J.-P. Delahaye, Les simplificateurs de π, 2015.
- A. Raz et al., A slice of π : An exploratory neuroimaging study of digit encoding and retrieval in a superior memorist, Neurocase, vol. 15(5), pp. 361-372, 2009.
- J.-P. Delahaye, Le fascinant nombre π, Belin/Pour la Science, 1997.
- M. Neveux, Le nombre d’or, radiographie d’un mythe, Seuil, 1995.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Jean-Paul Delahaye
Professeur émérite d'informatique à l'Université des Sciences et Technologies de Lille (Lille 1) et chercheur au Centre de recherche en informatique, signal et automatique de Lille (CRIStAL).