Calculer la courbure d’un maillage
La courbure : quelques définitions
Considérons un point p appartenant à une surface lisse S. Choisissons maintenant un vecteur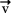 
tangent à la surface en p. Si on coupe la surface par le plan perpendiculaire à celle-ci, qui passe par p, et qui contient 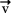, on obtient une courbe tracée sur la surface. La courbure de cette courbe au point p s’appelle la courbure normale de S au point p dans la direction 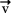. Quand on fait tourner 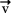, la courbure normale atteint une valeur maximale, la courbure maximale, et une valeur minimale, la courbure minimale. Les directions pour lesquelles ces valeurs sont atteintes s’appellent les directions principales, qu’on peut voir en gras sur la figure.
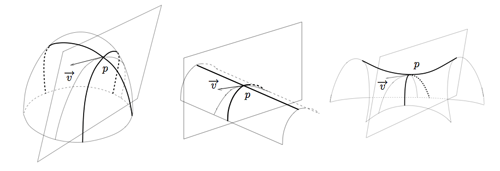
Quelques exemples de courbures.
Dans le dessin du milieu, la courbure minimale est égale à zéro, et elle est atteinte quand 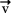est parallèle à l’axe du cylindre. La courbure maximale, quant à elle, est obtenue dans la direction perpendiculaire, et vaut l’inverse du rayon du cylindre. Dans la surface de droite, on voit que la courbure minimale est négative et la courbure maximale est positive, puisqu’il y a un changement de concavité.
À partir des courbures maximale et minimale, on peut définir deux nombres importants : la courbure moyenne, qui est la moyenne des deux, et la courbure de Gauss, qui est le produit des deux. La courbure moyenne a une interprétation physique, dont on peut donner une idée par l’image suivante : si on plonge une boucle en fil de fer (de forme quelconque) dans de l’eau savonneuse, alors le film de savon qui s’appuiera dessus aura une courbure moyenne nulle en tout point.
Film de savon obtenu en plongeant une boucle de fil de fer dans de l’eau savonneuse.
Expérience et photo : Jean-Marie Dendoncker.
La courbure moyenne de ce film de savon est nulle, comment cela s’explique-t-il ?
Un film de savon s’appuyant sur une courbe en 3D va tendre à minimiser son aire, un peu comme un élastique tendu entre deux points adopte la forme de longueur minimale joignant ces deux points, à savoir, bien sûr, un segment de droite. Autrement dit, l’élastique aura une courbure nulle. La propriété analogue pour les films de savon est que la courbure moyenne sera nulle. Cela se démontre par l’absurde : on peut montrer que si la courbure moyenne n’était pas nulle, alors on pourrait déformer légèrement le film de savon de sorte que son aire diminue, ce qui contredirait le fait que l’aire du film est minimale.
Attention, avoir une courbure moyenne nulle ne signifie pas être plan, mais plutôt que les courbures principales sont égales en valeur absolue, mais de signe opposé.
Quant à la courbure de Gauss, on voit qu’elle est positive pour la surface de gauche (et pour toute les surfaces « bombées »), nulle pour celle du milieu, et négative pour celle de droite. (Pour un exemple concret de surface à courbure de Gauss négative, regardez une feuille de salade de près.) Un théorème important de C.F. Gauss affirme (en particulier) que si vous froissez une feuille de papier, alors la surface obtenue aura une courbure de Gauss égale à zéro en tout point.
Du lisse au discret
Courbure en p : cas où p est sur une arête du maillage.
Supposons maintenant qu’on veuille calculer la courbure d’une surface représentée par un maillage très fin. Si le point p considéré tombe dans l’intérieur d’un triangle, alors la courbure du maillage en ce point est bien sûr égale à zéro dans toutes les directions. Si p est sur une arête du maillage, c’est-à-dire à la charnière entre deux triangles, alors la courbure est nulle dans la direction de l’arête. Par contre, si on coupe la surface dans une direction différente de celle de l’arête, alors on obtient une courbe présentant un angle vif, qu’on peut voir comme une courbe de courbure infinie. Si le point p tombe sur un sommet du maillage, alors la situation est encore plus compliquée. Selon les cas, on obtient donc soit zéro, soit l’infini, ce qui ne nous renseigne pas beaucoup !
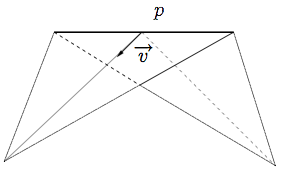
La « quantité totale » de courbure est égale à l’angle entre le premier segment de la portion et le dernier.
L’approche qui consiste à se focaliser sur un point précis p est donc vouée à l’échec. Pour sortir de cette impasse, il faut prendre du recul et regarder le maillage à une échelle plus grande. Illustrons cette idée par l’exemple des courbes polygonales, les analogues unidimensionnels des maillages. Comme précédemment, la courbure est nulle sur les segments qui composent la courbe, et infinie sur les sommets. Par contre, si on considère une portion de cette courbe, il est intuitivement clair que la « quantité totale » de courbure sur cette portion (en gras sur la figure) est égale à l’angle entre le premier segment de la portion et le dernier.
Cette idée, très simple dans le cas des courbes, se transpose au cas des surfaces : au lieu de se focaliser sur un point, on essaie de déterminer la quantité totale de courbure sur une région donnée. L’extension au cas des surfaces est toutefois bien plus compliquée que pour les courbes. On obtient ainsi des formules donnant la quantité totale de courbure moyenne, ou de courbure de Gauss, sur une région d’un maillage.
Ces formules, connues depuis plusieurs décennies, permettent d’obtenir les courbures maximale et minimale de la surface, mais par contre ne disent rien sur les directions dans lesquelles ces courbures sont atteintes. Or ces directions principales sont capitales pour certaines applications, par exemple le remaillage de surfaces. Ce manque a été comblé très récemment, et on dispose aujourd’hui de formules simples permettant de les obtenir en calculant le tenseur de courbure.
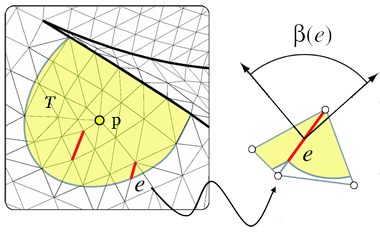
Pour un point p, ce que l’on recherche, ce sont la normale à la surface et les directions principales en p. Pour trouver ces directions, on considère une petite portion de maillage T, qui entoure ce point p, et on s’intéresse en particulier aux arêtes e qui sont dans cette portion de maillage. Pour chacune de ces arêtes, on appelle ß(e) l’angle dièdre, c’est à dire l’angle formé par les normales aux deux faces incidentes à cette arête. Cet angle est positif s’il est convexe ou négatif s’il est concave. On définit également un vecteur unité e parallèle à l’arête e, ainsi que le vecteur et qui est la transposée de e.
À partir de ces éléments, on calcule le tenseur de courbure HT de la portion de maillage T par la formule suivante :
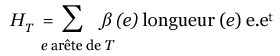
On obtient ainsi une matrice 3×3, et en la diagonalisant, on obtient une approximation des directions recherchées. La normale correspond à la plus petite valeur propre en valeur absolue.
 |
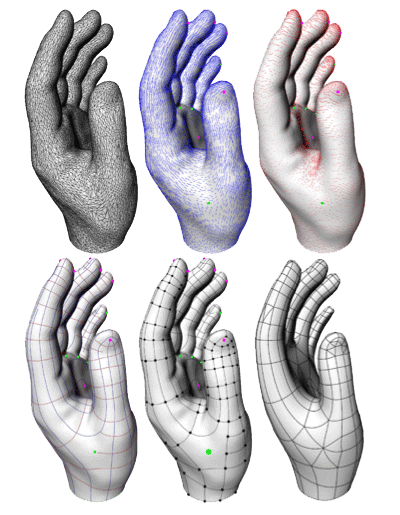
Remaillage d’une main.
À partir d’un maillage fin et irrégulier d’une main (en haut à gauche), on extrait les directions principales (minimales en bleu, maximales en rouge). Puis on trace deux réseaux de lignes tangentes à ces champs de directions, en choisissant l’espacement entre les lignes en fonction de la courbure (en bas à gauche). À partir de ces réseaux, on déduit un nouveau maillage de la surface constitué de quadrilatères (en bas à droite). On peut montrer que ce maillage tend à optimiser la qualité d’approximation, à nombre de quadrilatères fixé.
Voici pour terminer un exemple concret des directions principales obtenues par ces formules, à partir d’un maillage d’une célèbre statue de Michel-Ange. Le lecteur remarquera que ces directions permettent à elles seules de voir la forme tridimensionnelle de la statue !
Les directions principales de courbure mises en évidence à partir du maillage du David de Michel-Ange.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !
