Compression de maillages
Comment comprime-t-on les formes sur un ordinateur ? En se limitant au cas des maillages de surfaces – une représentation très répandue pour modéliser des formes, ce document décrit une technique de compression particulièrement adaptée au stockage sur disques durs, et utile aussi pour faciliter la transmission par réseau.
1. Représentation des formes
Les capacités d’un ordinateur, aussi puissant soit-il, sont limitées en stockage, mémoire et puissance de calcul. Comment représenter des formes complexes avec ces limitations ?
Maillages de surfaces
La première étape consiste à choisir de ne représenter que le bord, la surface des formes à représenter. C’est suffisant pour un grand nombre d’applications, comme la visualisation d’objets opaques. Une seconde étape consiste à décomposer la surface en primitives géométriques simples, des polygones. On appelle maillage cet ensemble de polygones, reliant un ensemble de points, les sommets des polygones. Les maillages composés uniquement de triangles sont courants du fait de leur simplicité. Le nombre de polygones représentable par l’ordinateur étant limité, on ne peut en pratique qu’espérer approcher la surface originale. C’est toutefois exploitable à condition d’utiliser un nombre suffisant de polygones pour l’application visée.

Différents maillages de la statue du David de Michel-Ange, du plus simple au plus détaillé.
Les maillages sont très répandus dans les applications qui exploitent des formes. Il n’est pas rare d’utiliser des maillages comprenant des milliers de polygones pour des jeux en trois dimensions – une carte graphique moderne peut ainsi afficher 180 millions de triangles par seconde – voire plusieurs millions pour des simulateurs de vols. Les maillages sont aussi devenus un outil clé de l’ingénierie numérique, en permettant la modélisation de formes complexes, leur visualisation et la simulation de phénomènes physiques.
L’ingénierie traditionnelle construit un prototype physique (parfois une maquette), et élabore des expériences comme la résistance des matériaux, les mesures de température, les tests de pression. L’ingénierie numérique substitue à la fois le modèle numérique au prototype physique, et le calcul à l’expérience. Ainsi, l’ingénieur accélère le cycle de conception en « essayant le réel », pour mieux concevoir et anticiper. Le maillage y joue le rôle de support pour le modèle défini pour la simulation.
 |
 |
 |
 |
 |
 |
 |
|
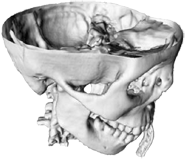
| Visualisations pour la médecine, l’histoire de l’art, la topographie, les jeux vidéo, les boutiques virtuelles, la conception, les simulateurs de vol : les applications des maillages sont multiples. | |||
Le développement vertigineux des capacités des ordinateurs autorise la modélisation de maillages de plus en plus précis, et la visualisation de formes de plus en plus complexes. Prenons l’exemple de la statue du David de Michel-Ange. 700 000 triangles suffisent pour reconnaître la statue dans une application multimédia, mais il en faut près de deux milliards pour retrouver les traces de l’outil utilisé par le sculpteur pour une application en histoire de l’art (Digital Michelangelo).
Cette évolution, qui offre un gain en fidélité pour la simulation, et en réalisme pour la visualisation par images de synthèse, s’accompagne d’une explosion des tailles des fichiers utilisés pour représenter les maillages (plus de 32 milliards d’octets pour la statue du David en très haute résolution). La compression de maillage devient alors essentielle pour exploiter de telles quantités de données.

Approximation de la statue du David par un maillage comprenant 700 000 triangles et 350 000 sommets. (La statue réelle mesure cinq mètres de haut.)
La compression est motivée par le stockage et les applications en réseau. En effet, le débit d’un réseau est limité, voire variable dans le temps, en fonction de l’encombrement. On cherche en particulier à réduire la latence, le temps d’attente lié au temps de transmission. Il en résulte une meilleure qualité de service, l’objectif prioritaire d’un opérateur de télécommunications.
Représentation d’un maillage
Avant de détailler la compression, voyons comment un maillage de surface peut être représenté simplement dans un ordinateur. Le fichier de description du maillage contient les informations sur les deux composantes principales du maillage, sa géométrie et sa connectivité.
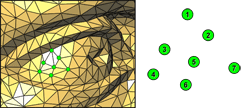
- La géométrie correspond à une liste de points, les sommets des polygones. Cette liste décrit les coordonnées tridimensionnelles (x,y,z) des points :
x1 y1 z1 (sommet 1) x2 y2 z2 (sommet 2) x3 y3 z3 (sommet 3) ...
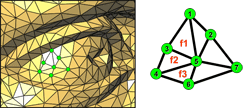
- La connectivité décrit comment les points sont reliés entre eux pour assembler les faces. Un triangle relie trois points, un quadrilatère relie 4 points, un pentagone relie 5 points, etc. Chaque face est décrite par la liste de ses sommets, chaque sommet étant représenté par son indice dans la liste de points et non par ses coordonnées. On parle de format indexé. La connectivité est donc une information combinatoire, car elle ne consiste qu’en une information d’identification de sommets dans une liste finie de points.
1 3 5 (face 1) 3 4 5 (face 2) 4 6 5 (face 3) ...
Quelle taille de fichier pour un format indexé ?
On peut calculer la taille d’un fichier d’un format indexé en nombre de bits par sommet. Prenons le cas d’un maillage triangulaire. La liste des sommets énumère trois coordonnées (x,y,z) par sommet. Si pour représenter chaque coordonnée, on utilise des nombres flottants stockés sur 32 bits – un format standard pour le calcul en virgule flottante – alors chaque sommet utilisera 3 x 32 = 96 bits. Il y a environ deux fois plus de faces (ou triangles) que de sommets. Si on énumère pour chaque triangle trois indices entiers positifs ou nuls stockés sur 32 bits, il en résulte 2 x 3 x 32 = 192 bits par sommet pour l’information combinatoire. La somme des informations combinatoire et géométrique résulte en 192 + 96 = 288 bits par sommet. Par exemple, la statue du David comprenant 700 000 faces occupe 12,6 Mo dans un format indexé binaire, et davantage pour le format indexé ASCII OBJ, qui nécessite 27 Mo car le fichier comprend des espaces, des caractères de contrôle (v et f) ainsi que des sauts de ligne.
Mentionnons qu’un format de fichier peut également représenter des attributs associés aux primitives du maillage, comme des couleurs par face ou par sommet, des coordonnées de texture, des matériaux qui gouvernent l’interaction entre la lumière et la matière lors du rendu, etc.
Un exemple de format indexé proposé par Alias Wavefront est le format ASCII OBJ. Chaque ligne commençant par le caractère « v » décrit un sommet du maillage. Chaque ligne commençant par le caractère « f » décrit une face du maillage. Une minuscule fraction du maillage triangulaire de la statue du David est donnée ci-dessous :
v 0.181171 -0.765913 -0.0161491 v 0.337181 -0.752783 -0.149217 v -0.0567281 0.940739 -0.114169 ... // 350 000 sommets f 146245 146293 146123 f 146126 146294 146165 f 146248 146294 146126 ... // 700 000 triangles
2. Choix d’une méthode
Compression de fichiers ?
Comprimer un maillage consiste à réduire la taille du fichier nécessaire à sa description. On distingue la compression sans perte, comme la compression de fichiers de type ZIP qui préserve l’intégrité des données originales, de la compression avec pertes qui autorise de supprimer certains détails avant la phase de compression. En pratique, ces détails sont supprimés lorsqu’ils sont jugés peu perceptibles lors de la visualisation, ou non pertinents pour la simulation. Pour certaines applications comme l’imagerie médicale, la compression avec pertes peut être légalement interdite, pour éviter par exemple des erreurs de diagnostic liées à la dégradation des images. Tout comme les images en JPEG sont comprimées au prix d’une distorsion plus ou moins importante suivant un critère paramétré par l’utilisateur, pour les maillages, on peut également régler le niveau de distorsion introduit par la compression.
On peut toujours appliquer une technique de compression de fichier de type ZIP sur les fichiers de description de maillages, mais nous verrons que les taux de compression sont bien supérieurs en élaborant des techniques de compression spécialisées pour les maillages.
Codage sur 32 bits ?
Un premier pas vers l’économie de bits consiste à regarder de plus près s’il est nécessaire de représenter les indices sur des entiers codés sur des mots de 32 bits. Un entier positif ou nul stocké sur 32 bits peut représenter des nombres entre 0 et (232-1 = 4 294 967 295) soit plus de 4 milliards. C’est bien plus qu’il n’en faut pour indexer les 350 000 sommets du maillage illustré ci-dessus, pour lequel des indices représentés sur 19 bits suffisent, car 350 000 est compris entre 218 et 219. En utilisant un codage à longueur adaptée, qui choisit des nombres avec un nombre de bits adapté au nombre de possibilités distinctes à représenter, il en résulterait un total de 210 bits par sommet. Ceci n’introduit aucune différence avec la représentation initiale.
Un second pas consisterait à réduire la taille occupée par les coordonnées des sommets, mais cela réduit la précision des nombres et introduirait une distorsion potentielle par rapport à la représentation initiale.
Il y a mieux à faire avant.
Compression monorésolution
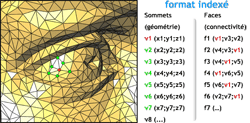
La compression sans perte consiste uniquement à supprimer la redondance présente dans la description originale du maillage. Dans le cas d’un format indexé, on peut voir que des indices se répètent pour la connectivité, proportionnellement à la valence des sommets (la valence d’un sommet correspond au nombre d’arêtes incidentes). Voyons s’il est possible de comprimer avec une technique de codage usuelle la séquence d’indices des sommets utilisée pour représenter les faces.
Codage entropique
Une méthode très répandue de compression, appelée codage entropique, consiste à associer à chaque symbole un code dont la longueur dépend de sa probabilité d’apparition. L’idée est que si l’on associe un code très court à un symbole très fréquent, alors l’économie de bits peut être substantielle. Par exemple dans la langue française, la lettre e est plus fréquente que la lettre z. En affectant un code plus court pour le e que pour le z, on peut réduire la longueur totale d’un texte. C’est déjà ce que l’on retrouve dans le code Morse, où le e est codé par « . » tandis que le z est codé par « – – .. ».
On peut même mesurer la compressibilité d’une séquence de symboles en mesurant son entropie, c’est-à-dire le nombre minimal de bits nécessaires à l’encodage d’un symbole.
L’entropie se calcule selon la formule suivante :
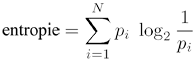
où N est le nombre total de symboles distincts (on parle aussi d’excursion des symboles), et pi est la probabilité d’apparition du i-ème symbole. De cette formule, on peut énumérer les facteurs entrant en jeu :
- les propriétés statistiques des symboles (leur distribution) : moins les symboles sont équiprobables, plus la source est compressible ;
- l’excursion des symboles (le nombre de symboles distincts, noté N) ;
- le nombre total de symboles à coder, à multiplier par l’entropie e pour obtenir le nombre total de bits nécessaires à l’encodage de la séquence.
Notez bien que dans le cas de symboles équiprobables, les longueurs de codes sont identiques. Le codage entropique n’apporte alors pas de compression par rapport à la représentation initiale.
Si l’on suppose que les maillages sont assez réguliers, c’est-à-dire que la plupart des sommets ont des valences proches, alors les indices pour la connectivité ont tendance à se répéter un même nombre de fois. On se trouve alors dans le cas d’une distribution équiprobable, et il y a donc peu d’espoir pour comprimer directement cette séquence.
Codage par transformée
Une alternative consiste à opérer une transformation sur la séquence initiale, afin d’opérer une modélisation statistique propice à un codage efficace. Il s’agit de modifier la distribution des occurrences des symboles, c’est-à-dire les probabilités d’apparition de ces symboles dans la nouvelle représentation. On parle de codage par transformée, très utilisé pour la compression du son et des images. La séquence initiale de symboles est remplacée par une autre, que le décodeur saura traduire en un maillage identique à l’original. Un codage entropique est ensuite appliqué à la nouvelle séquence. Si la nouvelle séquence de symboles présente une distribution moins uniforme, moins de symboles distincts, moins de symboles au total que la séquence originale, alors le gain en compression peut être spectaculaire.
Codage de la connectivité
Concrètement, la connectivité est comprimée par une transformée de la séquence initiale d’indices en une liste de degrés des faces (le nombre d’arêtes qui les bordent) et de valence des sommets (le nombre d’arêtes incidentes), plus un faible nombre de symboles accidentels. L’idée d’opérer une telle transformation a été introduite par Touma et Gotsman en 1998 pour les maillages triangulaires. Elle tire parti de l’observation qu’un maillage exhibe une faible dispersion en valence, d’autant plus que le maillage est régulier. Cette faible dispersion est liée d’une part aux algorithmes de maillages, et d’autre part à la formule d’Euler pour les maillages de surfaces, qui lie les nombres de sommets, d’arêtes, de faces, de trous et de composantes connexes. Cette formule contraint la valence moyenne des sommets à être proche de 6 dans le cas triangulaire – sachant que la valence minimale est de 3 pour un sommet intérieur, et de 2 pour un sommet du bord.
Dans sa version complète, la formule d’Euler s’écrit ainsi :
V – E + F + B = 2 (C – G)
où V désigne le nombre de sommets
E le nombre d’arêtes
F le nombre de faces
B le nombre de bords
C le nombre de composantes connexes
G le genre du maillage (c’est-à-dire le nombre de poignées).
Dans sa version simplifiée, s’il n’y a pas de bords, et que le genre est 0 (il s’agit d’une sphère topologique), la formule s’écrit :
V – E + F = 2
Dans le cas d’un maillage triangulaire, chaque face est bordée par trois arêtes, et une arête est incidente à deux faces. On a alors :
3 F = 2 E
d’où E = F + V – 2 = 2 E / 3 + V – 2
d’où 3 E = 2 E + 3 V – 6
donc E = 3 V – 6
Chaque arête étant incidente à deux sommets, on a alors :
∑ valences = 2 E = 6 V – 12
Lorsque le nombre de sommets est grand, on néglige le nombre 12, cette formule indique alors que la moyenne des valences est de 6.
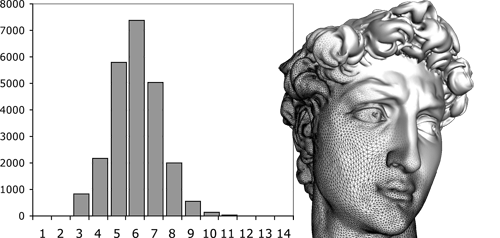
La distribution des valences des sommets de ce maillage présente une faible dispersion autour de la moyenne 6.
Dans le cas d’un maillage triangulaire, la séquence des degrés des faces est une longue suite de 3, donc d’entropie nulle, puisque le symbole 3 apparaît avec la probabilité 1. Si le maillage est parfaitement régulier, comme le maillage de droite ci-dessous, la séquence de valences des sommets est une suite de 6, également d’entropie nulle. Avec un grand nombre de sommets, le nombre de bits par sommet tend vers zéro, et le nombre total de bits utilisés par ce maillage après compression est donc négligeable.
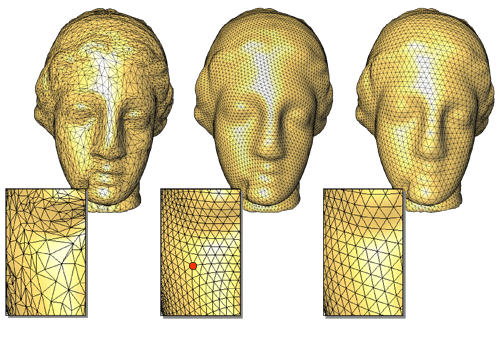
De gauche à droite : un maillage irrégulier, presque régulier (zoom autour d’un sommet de valence 7) et parfaitement régulier (tous les sommets ont une valence égale à 6).
Le gain en compression obtenu présente un facteur proche de 100 en moyenne pour la connectivité des maillages (soit 2.8 bits par sommet en moyenne contre 288 pour une représentation indexée). Même si le facteur de compression est moins impressionnant pour la géométrie (un facteur 3 dans le cas sans perte), c’est en moyenne deux fois plus performant qu’une méthode de compression de fichiers.
Phase de codage
Voyons tout de suite dans le détail comment cette transformée opère. L’algorithme de codage choisit une face initiale du maillage, la marque comme région conquise, et procède par expansion de cette région face par face, par pivot successif autour des sommets situés sur le bord de la région. La chaîne d’arêtes reliant ces sommets est appelée liste active, elle est représentée en mémoire par la liste chaînée des sommets.
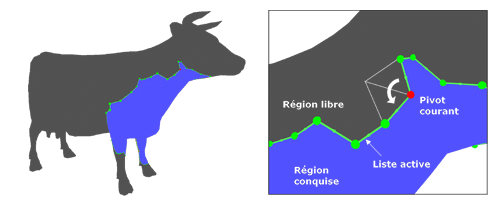
Une étape d’expansion de la région conquise dans le cas d’un maillage triangulaire.
Lorsqu’un nouveau sommet est inséré dans la liste active, un symbole correspondant à sa valence est généré. Lorsqu’une nouvelle face est conquise, un symbole correspondant à son degré est généré.
Lorsque le sommet pivot courant est incident à une seule face non conquise, cette dernière est marquée conquise, et le pivot est supprimé de la liste active. Notons que cette opération ne nécessite pas de génération de symbole, le décodeur pouvant la déduire à partir des informations de valence des sommets.
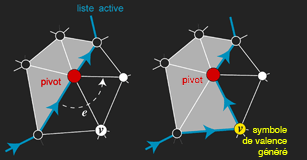 |
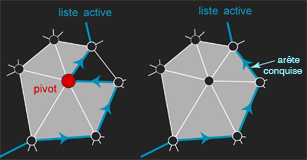 |
| Opération élémentaire d’expansion dans le cas d’un maillage triangulaire. | Ici, la dernière face est marquée conquise, et le pivot est supprimé de la liste active. |
Deux nouveaux types d’événements peuvent se produire au cours de l’expansion. Le premier se produit lorsque le prochain sommet à conquérir se situe sur la liste active. Dans ce cas, un symbole spécial « séparation » est émis, et la liste active est scindée en deux listes d’orientations opposées. L’une reste active, et l’autre est mise en attente dans une pile de listes inactives.
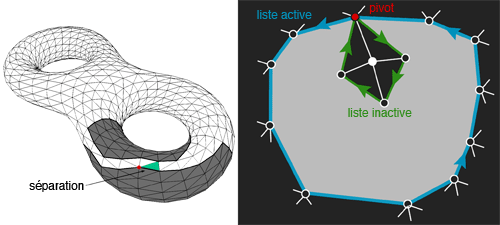
Séparation de la liste active.
Le second nouveau type d’événement correspond au cas où le prochain sommet à conquérir se trouve dans une liste inactive. Dans ce cas, un symbole spécial noté « fusion » est émis, et les deux listes correspondantes sont fusionnées. Il y a en pratique autant de codes « fusion » que de « poignées » dans le maillage (deux dans le cas du double tore ci-dessous).
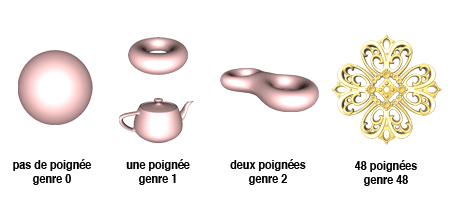
La topologie est une science qui étudie les propriétés géométriques invariantes d’un objet quand celui-ci est étiré, tordu ou rétréci de manière continue. Un tore (une chambre à air ou un beignet) et une tasse sont ainsi équivalents.
Une tasse peut être obtenue en perçant deux trous sur une sphère et en ajoutant une anse (ou poignée, c’est-à-dire un cylindre dont les deux extrémités coïncident avec les trous). On peut transformer une tasse en un double beignet en ajoutant encore une poignée, etc.
Le genre d’un objet se définit en fonction de son nombre de poignées.
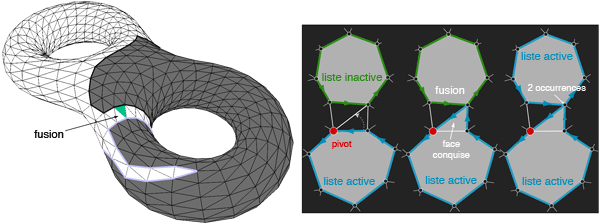
Fusion de la liste active et d’une liste inactive.
Phase de décodage
Plaçons-nous maintenant dans le cas du décodeur, qui ne dispose que des symboles de degré des faces et de valence des sommets pour reconstruire la connectivité originale du maillage. L’animation suivante illustre la phase de décodage.

Principe du décodage : le décodeur utilise successivement les informations sur la valence des sommets et sur le degré des faces pour reconstituer la connectivité du maillage.
Analyse
Afin de prouver la validité de leur méthode dans le cas général, les chercheurs se sont interrogés sur l’entropie maximale atteignable par la séquence de valences des sommets, en se limitant dans un premier temps au cas des maillages triangulaires. À partir de la formule de l’entropie et de la formule d’Euler, ils ont déduit que la distribution des symboles est une exponentielle décroissante, avec une valeur d’entropie d’environ 3.24 bits par sommet. Un calcul similaire a été mené dans le cas des maillages polygonaux. La valeur trouvée coïncide avec l’entropie des graphes planaires calculée par une méthode énumérative dans les années soixante.
Codage de la géométrie : quantification et codage prédictif
Nous venons de décrire la compression de la connectivité. Il reste à comprimer la géométrie, c’est-à-dire les coordonnées des sommets. La première étape consiste à opérer une quantification uniforme.
La quantification uniforme des positions des sommets revient à arrondir chaque coordonnée sur une grille régulière. Le niveau de précision de la grille s’exprime en bits, une quantification sur 8 bits signifiant une grille avec 28 = 256 valeurs distinctes. Des pertes sont donc introduites à cette étape.
Après quantification, les positions des sommets sont codées par prédiction de type parallélogramme : chaque nouveau sommet conquis est prédit de manière à former un parallélogramme à partir du triangle incident (voir figure ci-dessous). Seul le résidu après prédiction (la flèche rouge sur la figure) est alors encodé.
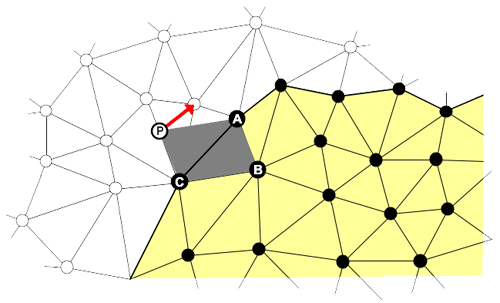
Codage prédictif : le point P est calculé à partir du triangle ABC, le résidu après prédiction correspond à la flèche rouge.
Ainsi, l’information géométrique (au départ, les coordonnées des sommets) est convertie en une suite de résidus après prédiction, qui tire parti de l’ordre du parcours sur le maillage lors du codage de la connectivité. Il s’agit une nouvelle fois de modélisation statistique, puisque dans le cas d’une distribution uniforme des sommets, les résidus sont concentrés autour de zéro, et donc propices à une compression entropique efficace.
Codage arithmétique
Les deux étapes précédentes opèrent un encodage propice à une compression efficace. L’étape finale comprime les trains de symboles résultant en un fichier binaire, par codage arithmétique. Le codage arithmétique est un raffinement du codage entropique, qui présente l’intérêt de coder chaque symbole sur un nombre fractionnaire de bits, en exploitant finement les probabilités des symboles. À chaque symbole correspond un mot de code d’autant plus court que sa probabilité est élevée.
Résultat
La statue du David, avec ses 700 000 triangles, est codée avec 29.92 bits par sommet (soit 2.15 bits pour la connectivité, 27.78 pour la géométrie), en quantifiant la géométrie sur 18 bits. Avec ce taux de compression, c’est près de 510 modèles de la statue du David que l’on peut stocker sur un CD-ROM ! C’est près de 10 fois moins d’espace disque que le format indexé, qui occupe 288 bits par sommet.
Conclusion
La méthode de compression monorésolution de maillages présentée ici permet une réduction de la taille des données par un facteur 10 sans entraîner de dégradations visuelles importantes. Mais ce n’est qu’une facette de la compression, qui peut recouvrir de nombreux aspects. En particulier, la compression progressive transforme un maillage en un flux de raffinements pour la transmission progressive sur les réseaux. La problématique devient alors l’optimisation du compromis entre débit et distorsion. Un autre axe de recherche important concerne la compression de maillages dans la mémoire de l’ordinateur. En effet, comprimer une forme pour le stockage ou la transmission est une chose, mais après décompression, un maillage volumineux occupe une place importante dans la mémoire pour l’affichage ou la simulation. Peut-on comprimer dans la mémoire la structure de données associée au maillage, tout en permettant de l’exploiter pour des applications ? Économiser toutes les ressources possibles, c’est toujours cohérent avec le leitmotiv des chercheurs en compression de données.
Nous vous proposons quelques références :
- si vous cherchez des notions générales sur la compression de données ;
- si vous voulez en savoir plus sur la compression de maillages.
Ces documents, en anglais, sont destinés à l’origine à un public de chercheurs.
- Benchmark de Martin Isenburg
- Recent Advances in Compression of 3D Meshes, Pierre Alliez and Craig Gotsman, chapitre du livre Advances in Multiresolution for Geometric Modelling, N.A. Dodgson and M.S. Floater and M.A. Sabin, Springer-Verlag 2005 (pages 3 à 26).
Remerciements à Martin Isenburg pour une partie des illustrations, et au projet Digital Michelangelo de l’université de Stanford pour le modèle 3D de la statue du David.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !
