
De Fourier à la reconnaissance musicale
Le succès planétaire de l’application mobile Shazam montre que la reconnaissance musicale par une machine est concrètement possible. Quelles sont ses limites ? Quelles améliorations peut-on imaginer dans ce domaine ? Mais surtout, quel rapport avec Fourier ?
Fourier et la représentation des sons
La transformée de Fourier est un formidable outil d’analyse des signaux musicaux. En particulier, elle permet d’obtenir une représentation Temps-Fréquence d’un enregistrement musical, appelée spectrogramme. En pratique, le spectrogramme est généré avec la TFCT (Transformée de Fourier à court terme) calculée sur des segments successifs de signal. Le spectrogramme permet ainsi de visualiser la variation au cours du temps des principales composantes fréquentielles de l’enregistrement musical (voir la figure 1 ci-dessous).
Le spectrogramme est ainsi une représentation caractéristique d’un enregistrement musical. Il est alors possible d’extraire à partir de cette représentation des « signatures » ou « empreintes » des morceaux de musique un peu à l’image des empreintes digitales pour l’identification de personnes. Les systèmes de reconnaissance musicale permettent ainsi de comparer la signature d’un morceau de musique inconnu à l’ensemble des signatures préalablement calculées et stockées dans une base de données.
- Choisir une succession d’instants t, par exemple tous les centièmes de secondes ;
- Autour de chaque instant, sélectionner un segment de signal. Chaque segment contiendra un nombre N d’échantillons et des segments adjacents se recouvriront partiellement ;
- Pour chaque segment, calculer sa transformée de Fourier, par exemple par l’algorithme de FFT (Fast Fourier Transform), ce qui conduira à N valeurs Xf dont on calculera ensuite le carré du module |Xf|2 ;
- Chaque coefficient |Xf|2 représente ainsi l’énergie à la fréquence f du segment de signal à l’instant t.
Extraire une empreinte musicale
Le spectrogramme contient beaucoup d’informations redondantes. Utiliser directement le spectrogramme comme empreinte musicale serait à la fois complexe et très largement sous-optimal. Il est en effet essentiel qu’une empreinte musicale contienne une information caractéristique de l’enregistrement musical qui soit à la fois compacte et discriminative. L’une des premières idées au cœur de la reconnaissance musicale est ainsi de découper le spectrogramme à l’aide d’une grille définissant des zones spectrotemporelles localisées. On peut ainsi définir l’empreinte musicale à partir des maximums d’énergie de chaque zone spectrotemporelle, avec par exemple un seul maximum par zone (comme illustré sur le bas de la figure 1 ci-dessous). Une empreinte musicale plus sophistiquée mais aussi plus performante va consister à répertorier des paires entre les maximums d’énergie de zones proches. Chaque paire de maximums spectraux ainsi définie constitue une « clé ». Un morceau est alors caractérisé par un ensemble de clés indexées dans le temps (c’est-à-dire avec leur instant d’occurrence t).
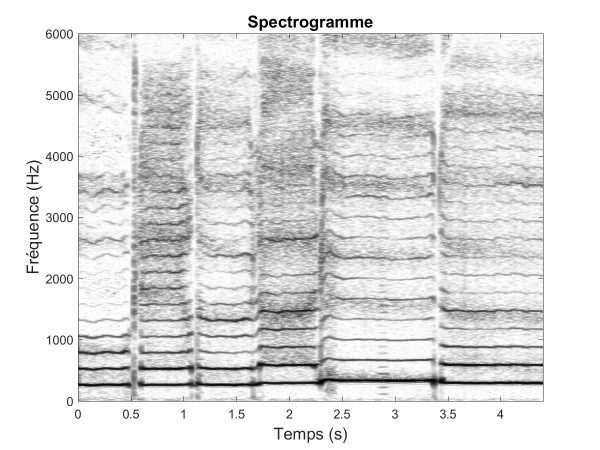
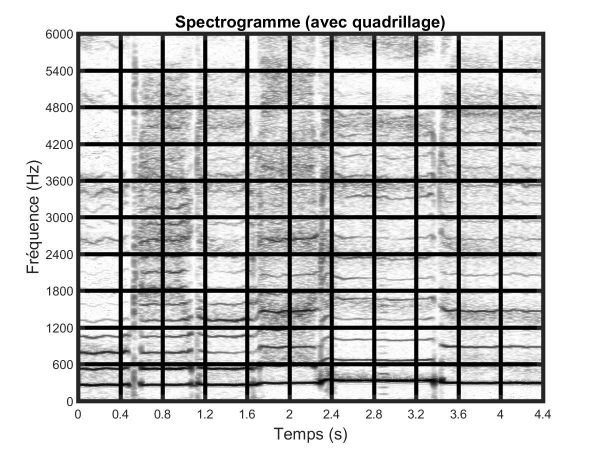
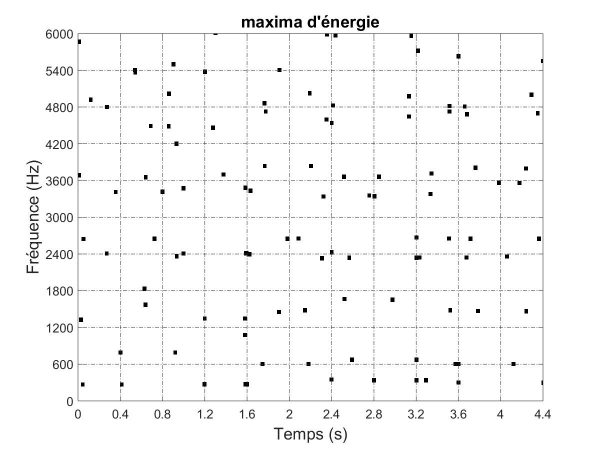
Figure 1. En haut, spectrogramme d’un enregistrement musical de la chanson Au clair de la lune chantée a cappella. Au milieu, pavage du spectrogramme en zones spectrotemporelles — la première zone en bas à gauche correspond au segment musical du début du morceau au temps 0.4 s et pour les fréquences comprises entre 0 et 600 Hz. En bas, dans chaque zone, on ne conserve qu’un maximum d’énergie dont la valeur est forcée à « 1 ». Pour des enregistrements simples de percussion, ces maximums seront principalement localisés au moment des frappes sur les instruments qui sont alors des instants d’énergie maximale très localisés. Cependant, dans le cas plus général d’un enregistrement polyphonique, il sera plus difficile de les relier directement à des concepts musicaux tels que le rythme ou les notes.
Reconnaître un morceau inconnu
La reconnaissance d’un morceau de musique pourrait se faire en comparant son empreinte avec toutes celles dites de référence qui sont en mémoire.
Néanmoins, l’enjeu d’un système de reconnaissance musicale est de pouvoir reconnaître un extrait musical au sein d’une collection contenant jusqu’à plusieurs dizaines de millions de titres. Dans ce cadre, il n’est pas envisageable de comparer l’extrait à chacune des références, le temps de calcul devenant largement prohibitif sur de telles collections.
Il est ainsi nécessaire de reposer sur ce qui est communément appelé un « index ». Construire un index consiste à réordonner les informations contenues dans les références. Dans notre cas, au lieu de stocker les données référence par référence, on associera à chaque clé possible l’ensemble des références la contenant ainsi que l’instant auquel cette clé apparaît dans la référence. Il devient alors très simple, à partir d’une clé, de retrouver toutes les références la contenant. Ce fonctionnement est le même que celui mis en œuvre lorsque l’on cherche les pages d’un livre contenant un terme précis grâce à l’index de mots-clés parfois fourni en fin d’ouvrage.
En réitérant cette opération, rapide, sur l’ensemble des clés de l’extrait inconnu on obtient un ensemble de références « candidates » possédant des clés en commun avec l’extrait. Néanmoins, l’extrait inconnu et les références auront en général une origine des temps différente (il est en effet courant que l’extrait n’inclue pas le début du morceau) et il convient donc de conserver l’information de décalage temporel entre l’apparition de la clé dans l’extrait inconnu et dans les différentes références. On peut ensuite chercher parmi ces références celle qui a le plus de clés en commun avec l’extrait, à décalage temporel constant (autrement dit, celle qui possède les mêmes clés avec la même succession temporelle).
-
Extraction des paires de maximums (avec leurs instants d’occurrence respectifs) du morceau à reconnaître. Chaque paire constitue une clé et est encodée sous laforme d’un vecteur [f1, f2, t2−t1] où(f1, t1) (resp. (f2, t2)) est la position spectrotemporelle du premier maximum (resp. du second maximum) ;
-
Recherche dans la base de l’ensemble des références candidates qui ont des clés communes avec celles du morceau à reconnaître. Pour chaque clé extraite, on notera le décalage temporel ∆t = t1 − tref où t1 et tref sont respectivement les instants du premier maximum de la clé dans le morceau à reconnaître et dans la référence candidate.
-
La référence qui a le plus de clés en commun à décalage temporel ∆t constant est le morceau reconnu (cf figure 2 ci-dessous pour un exemple d’histogramme pour 3 références candidates).
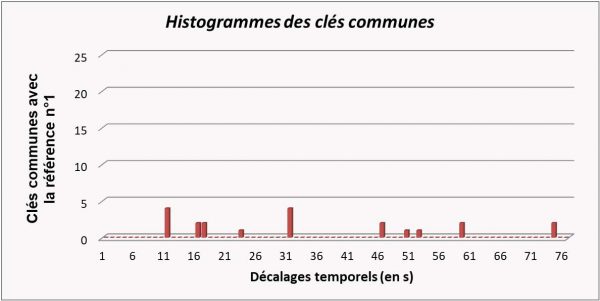
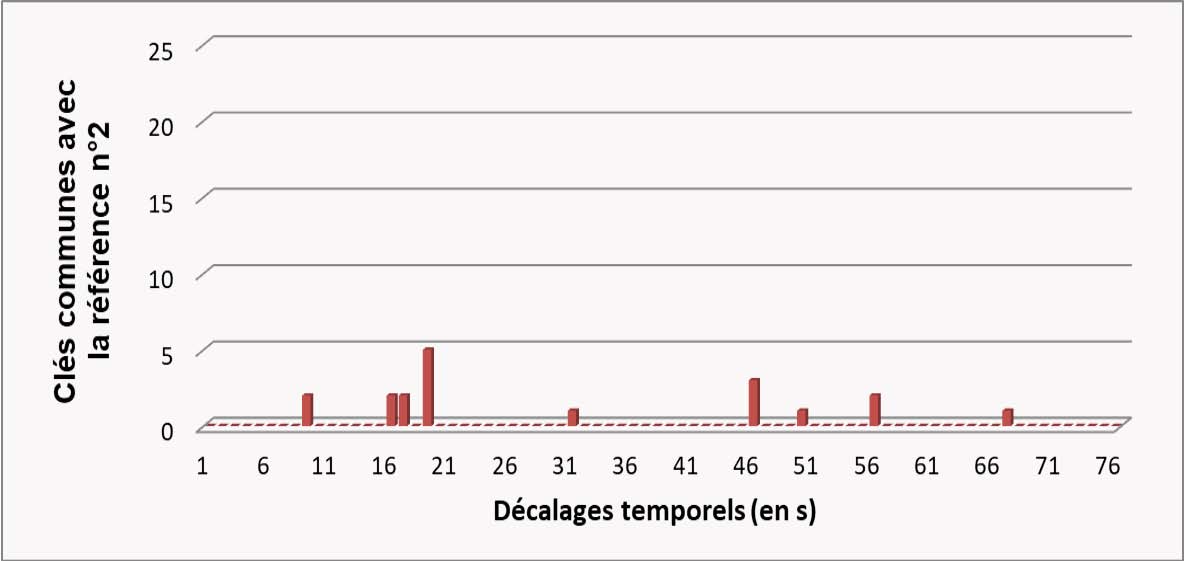
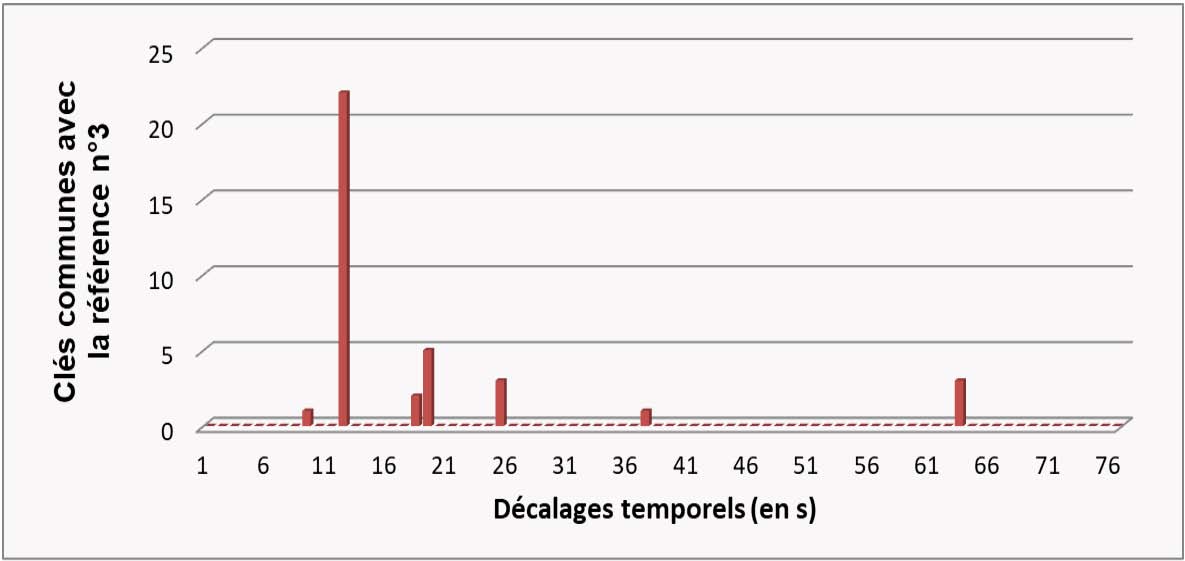
Figure 2. Exemple synthétique illustrant la reconnaissance : histogrammes des paires de maximums spectraux (ou « clés ») communes entre le morceau à reconnaître et trois morceaux de références de la base. Le morceau reconnu correspondra à la référence qui a le plus de clés communes pour un décalage temporel ∆t donné (en l’occurrence ici la référence nº3 qui possède plus de 20 clés communes avec un décalage identique de 12 secondes).
Si l’on veut, de plus, pouvoir indiquer que le morceau à reconnaître ne fait pas partie de la base de morceaux connus, il sera nécessaire de définir un seuil précisant le nombre minimal de clés communes qui doivent être trouvées pour prendre une décision de reconnaissance.
Performances et améliorations possibles
Cette méthode assez simple à l’origine de l’application Shazam obtient déjà d’excellents résultats. Par exemple un taux de bonne reconnaissance de 83 % a été obtenu dans une expérience menée en laboratoire sur l’analyse automatique de 7 jours d’une radio française et avec une base en mémoire de 7300 titres.
Cependant, cette expérience permet aussi de mettre en lumière certaines des limitations de cette méthode. Par exemple, une variation de la vitesse de lecture d’un titre (ce qui est couramment utilisé par les radios) va clairement affecter la reconnaissance. En effet, une augmentation de la vitesse de lecture va avoir pour effet de déplacer les paires de maximums vers les hautes fréquences (effet de modulation) et raccourcir le décalage temporel entre les deux maximums de la paire. C’est surtout le décalage fréquentiel qui sera d’ailleurs problématique en raison de la forme rectangulaire des zones spectrotemporelles qui induit une sensibilité plus faible au décalage temporel. Une autre limitation est liée au fait que l’on accorde autant d’importance à l’information en basses fréquences et en hautes fréquences. En effet, la transformée de Fourier ainsi que le pavage défini pour les empreintes donnent des zones spectrotemporelles d’égale extension en fréquence alors même que l’on sait que les capacités de l’oreille en résolution fréquentielle sont plus proches d’une échelle logarithmique.
Une des solutions à ces deux limitations a pu être trouvée en remplaçant la transformée de Fourier initiale par une transformée à Q constant. Cette transformée permet d’obtenir une représentation temps-fréquence dont la résolution fréquentielle diminue avec la fréquence et dont les indices de fréquence varient logarithmiquement. Il est ensuite nécessaire d’adapter l’encodage de l’empreinte mais, en reproduisant l’expérience décrite ci-dessus, les performances de reconnaissance grimpent à 97 %.
D’autres solutions ont aussi été proposées en appliquant des techniques de traitement d’images au spectrogramme. Les empreintes peuvent être calculées à partir de caractéristiques invariantes à l’échelle (comme par exemple les caractéristiques « SIFT » ou Scale Invariant Features Transform en anglais).
Il existe cependant une limitation plus difficile à résoudre. En effet, ces méthodes ne permettent pas de reconnaître une version réinterprétée du morceau original (version live ou nouvel enregistrement avec les mêmes musiciens) et bien sûr encore moins une reprise du morceau enregistrée par d’autres musiciens et potentiellement dans un genre musical différent. En effet, pour parvenir à résoudre ce problème il est nécessaire d’extraire des informations plus générales de contenu musical telles que la mélodie (la séquence des notes jouées par l’instrumentiste principal par exemple), l’harmonie (la séquence des accords joués par exemple), le rythme, etc.
Plusieurs méthodes proposent ainsi d’intégrer dans le calcul des signatures des indices liés à l’harmonie ou au rythme musical pour reconnaître non seulement les enregistrements identiques mais aussi identifier une grande proportion des morceaux réinterprétés.
Enfin, un certain nombre de travaux récents se concentrent sur la réduction de la taille mémoire et la maîtrise de la complexité de calcul des empreintes. En effet, ces deux aspects sont particulièrement importants pour pouvoir passer à l’échelle (c’est-à-dire permettre une utilisation sur des bases de plus en plus volumineuses) ou pour envisager une implémentation sur des terminaux mobiles de faible capacité.
Conclusion
Dans cet article, nous avons illustré le rôle central de la transformée de Fourier dans un système de reconnaissance musicale. Nous avons également vu comment on pouvait adapter cette représentation initiale pour obtenir à la fois une reconnaissance plus robuste aux modifications de vitesse de lecture d’un enregistrement et mieux prendre en compte certaines propriétés perceptives de l’oreille. Aujourd’hui, les performances des systèmes de reconnaissance musicale sont remarquables pour reconnaître un enregistrement connu mais restent limitées pour reconnaître une réinterprétation ou une reprise d’un morceau.
Nous avons esquissé quelques directions qui permettraient d’obtenir une reconnaissance plus intelligente, capable d’identifier les reprises. Ce problème représente clairement l’un des enjeux majeurs des futurs systèmes de reconnaissance musicale.
- Wang, A. An industrial-strength audio search algorithm. in Proceedings of the Conference of the International Society for Music Information Retrieval (ISMIR-2003)(Baltimore, US).
- Fenet, S., Richard, G. & Grenier, Y. A scalable audio fingerprint method with robustness to pitch-shifting. in Proceedings of the Conference of the International Society for Music Information Retrieval(ISMIR-2011) (Miami, USA).
- Six, J. & Leman, M. Panako: a scalable acoustic fingerprinting system handling time-scale and pitch modification. in Proceedings of the Conference of the International Society for Music Information Retrieval (ISMIR-2014) (Taipei, Taiwan).
- Zhang, X. et al. Sift-based local spectrogram image descriptor: a novel feature for robust music identification. EURASIP J. on Audio, Speech, Music. Process. 2015, 6 (2015). DOI 10.1186/s13636-015-0050-0.
- Fenet, S., Grenier, Y. & Richard, G. An extended audio-fingerprint method with capabilities for similar music detection. in Proceedings of the Conference of the International Society for Music Information Retrieval (ISMIR-2013) (Curitiba, Brazil, 2013).
- Malekesmaeili, M. & Ward, R. K. A local fingerprinting approach for audio copy detection. Signal Process. 98, 308 – 321 (2014). DOI.
- Sonnleitner, R. & Widmer, G. Robust quad-based audio fingerprinting. IEEE/ACM Transactions on Audio, Speech, Lang. Process. 24, 409–421 (2016). DOI.
- Yao, S., Niu, B. & Liu, J. Audio identification by sampling sub-fingerprints and counting matches. IEEE Transactions on Multimed. 19, 1984–1995 (2017). DOI.
- Plapous, C., Berrani, S.-A., Besset, B. & Rault, J.-B. A low-complexity audio fingerprinting technique for embedded applications. Multimed. Tools Appl. 77, 5929–5948 (2018).
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Gaël Richard
Professeur, membre du Laboratoire Traitement et Communication de l'Information (LTCI) de Télécom ParisTech, Université Paris-Saclay.

Sébastien Fenet
Chercheur en traitement du signal au sein du Laboratoire Traitement et Communication de l'Information (LTCI) de Télécom ParisTech, Université Paris-Saclay.

Yves Grenier
Enseignant-chercheur au sein du Laboratoire Traitement et Communication de l'Information de Télécom ParisTech, Université Paris-Saclay.