Démêler les nœuds avec des boucles

Si vous pratiquez le tricot, il vous est peut-être déjà arrivé, suite à l’action malicieuse d’un animal, d’un enfant ou d’un lave-linge, d’être confronté à ce genre de crise :

Peut-être trouvez-vous cela d’ailleurs relaxant de mettre de l’ordre dans un tel chaos : il existe sur Internet plusieurs communautés en ligne consacrées à ce hobby et l’on y trouve des comparatifs avant/après très satisfaisants à contempler.

Mais pour le commun des mortels, dénouer n’est pas une partie de plaisir. En ces temps d’IA omniprésente, il est tentant de se demander si les ordinateurs pourraient nous enlever cette épine du pied.

Des bobines de ficelle à la théorie des nœuds

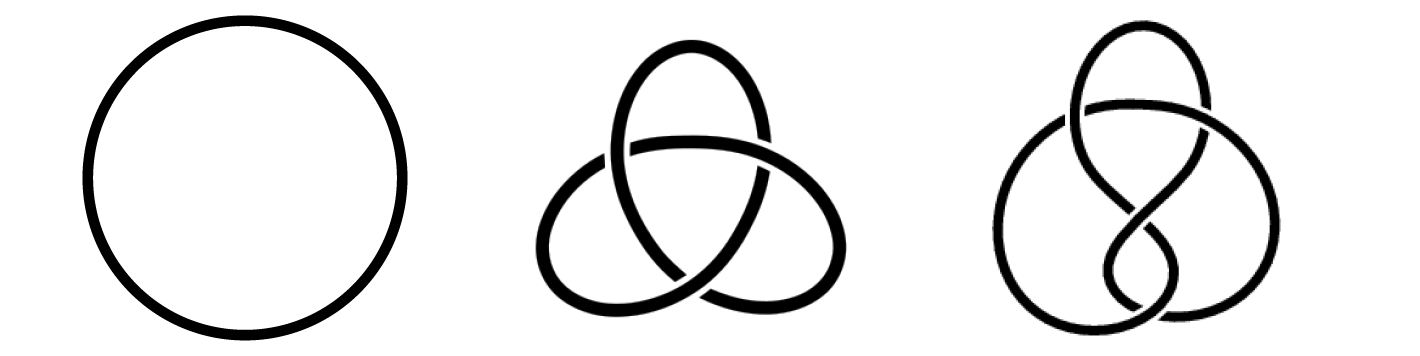
Il se trouve que l’étude des nœuds forme un domaine mathématique à part entière, assez méconnu du grand public, la théorie des nœuds. Son objet d’étude principal ressemble comme deux gouttes d’eau à nos ficelles, mais à une différence importante près : d’un point de vue mathématique, l’étude de ces ficelles n’est pas bien intéressante car elles sont, en théorie du moins, très faciles à démêler. En effet, il suffit de trouver une extrémité, de s’armer de patience et de la suivre et le tour est joué. C’est pourquoi on étudie plutôt des nœuds où les deux extrémités sont attachées ensemble (NDLA : un lecteur critique objectera peut-être que le problème dont je parle est donc fondamentalement différent de mes ficelles introductives. Ce n’est pas faux mais pas tout à fait vrai non plus : dans de nombreux cas, par exemple avec une corde d’escalade, on n’a aucune envie d’aller chercher très loin un brin libre pour dénouer une corde et on préfèrerait défaire le nœud là où il est. Cela revient à avoir attaché les bouts). On considère ensuite que deux nœuds sont équivalents si on peut déformer l’un en l’autre, et comme les bouts ont été attachés, il apparaît différentes familles de nœuds. Je vous présente le nœud trivial (ou nœud dénoué), le nœud de trèfle et le nœud de huit, et il y en a plein d’autres.

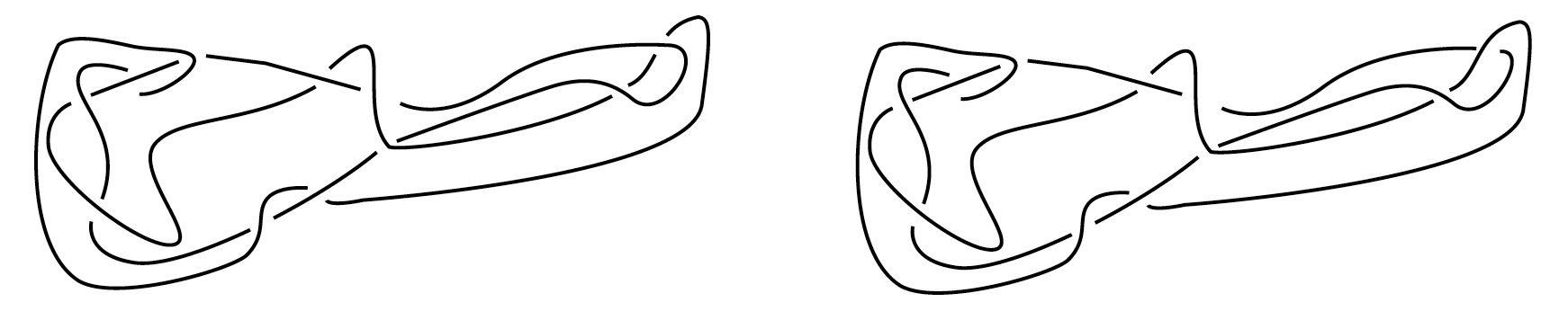
Ces bouts attachés n’empêcheront pas votre chat de sévir. D’ailleurs celui-ci a bien travaillé : après une après-midi très occupée, il vous montre les deux nœuds suivants. Pouvez-vous déterminer si l’un d’eux est trivial ? La réponse sera donnée un peu plus loin.

L’ordinateur à la rescousse

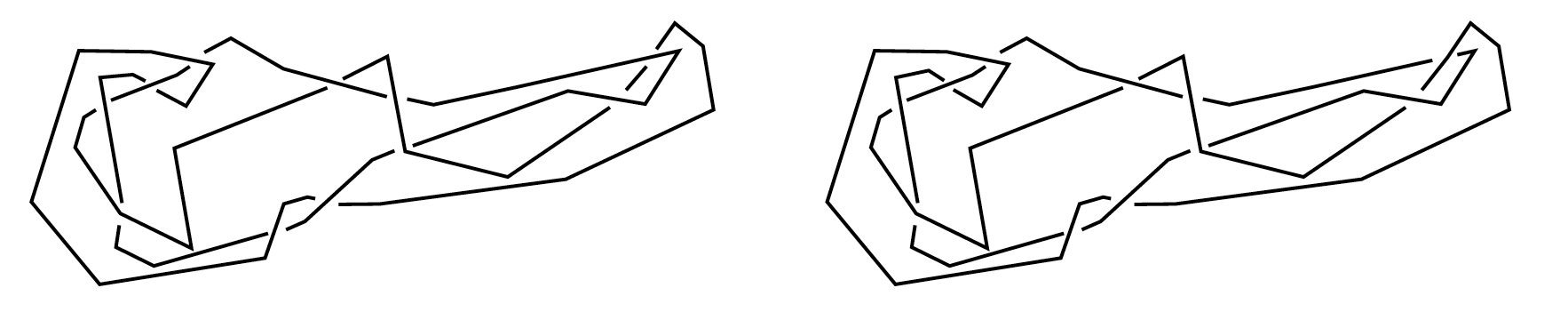
Pour demander de l’aide à un ordinateur, il faut d’abord trouver un moyen de lui décrire ces nœuds : un algorithme travaille sur des entrées discrètes, c’est-à-dire avec un nombre fini d’informations. Pour discrétiser un nœud, une méthode simple est de le décrire par une courbe polygonale : une succession de segments dans le plan, décrits par les coordonnées de leurs extrémités où l’on ajoute à chaque croisement une information décrivant quel brin passe au-dessus de l’autre. De façon plus formelle, il s’agit d’un graphe planaire 4-régulier où l’on a décoré chaque sommet d’un bit encodant le type de croisement.
Nos exemples deviennent alors plutôt comme cela.

Que faire maintenant ? Mistral, ChatGPT et leurs amis ne vous seront pas d’une grande aide ici (essayez !). Et pour cause : le problème n’a rien d’évident. Dans un article célèbre, le fondateur de l’informatique théorique Alan Turing, joué par Benedict Cumberbatch dans le film The Imitation Game, dont on a déja parlé sur Interstices, écrivait en 1954 “No systematic method is yet known by which one can tell whether two knots are the same” (« Aucune méthode systématique n’est connue pour dire si deux nœuds sont les mêmes »). A-t-on fait des progrès depuis ?

Une boucle pour dénouer ?

Une approche naïve pour attaquer ce problème qui correspond à ce qu’on fait en pratique serait de manipuler le nœud un peu au hasard, en le déformant localement en espérant arriver quelque part. On peut décomposer de tels mouvements locaux en trois mouvements élémentaires, appelés mouvements de Reidemeister.

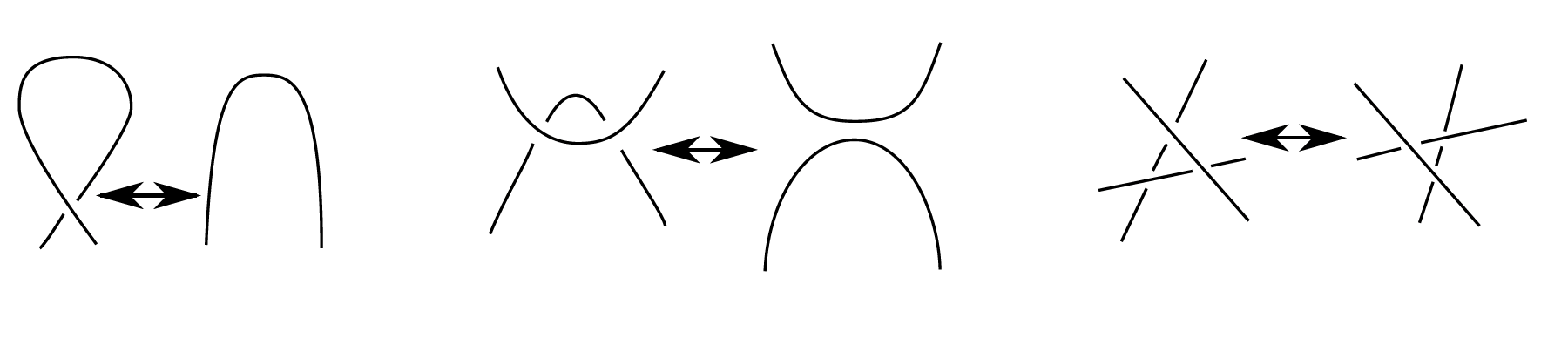
Figure 1 — Les trois mouvements de Reidemeister : le premier mouvement fait ou défait une boucle, le deuxième sépare ou superpose deux brins l’un au-dessus de l’autre et le troisième passe un brin au-dessus d’un croisement.

Un théorème fondamental de Kurt Reidemeister, prouvé en 1927, montre que si un nœud est trivial, on peut le démêler en appliquant ces trois mouvements un nombre fini de fois. Plus généralement, on peut toujours relier deux diagrammes de nœuds équivalents par une suite de mouvements de Reidemeister. Cela donne une idée de départ : pour démêler un nœud, on peut d’abord essayer tous les mouvements de Reidemeister disponibles à partir du nœud de départ. Si cela ne suffit pas, on essaye les suites de deux mouvements de Reidemeister consécutifs. Puis trois, puis quatre, et ainsi de suite. Le théorème nous garantit que si le nœud est trivial, cela finira par fonctionner. Bien sûr, ce n’est pas très efficace, et si le nœud n’est pas trivial, notre algorithme ne s’arrête jamais. En fait, une telle procédure ne s’appelle en général même pas un algorithme, mais plutôt un semi-algorithme, qui rend notre problème récursivement énumerable.

Un premier algorithme

Pour avoir un vrai algorithme, il nous faudrait une version quantitative du théorème de Reidemeister : certes, on peut démêler un nœud trivial avec un nombre fini de mouvements mais combien en faut-il ? Ce problème d’apparence très simple n’est encore aujourd’hui pas complètement résolu. Le meilleur résultat connu est un théorème assez récent de Marc Lackenby (datant de 2015) qui montre que si un nœud avec n croisements est trivial, il existe une suite d’au maximum (236 × n)¹¹ mouvements de Reidemeister qui le dénouent. Cela donne maintenant un véritable algorithme : il suffit d’essayer toutes les suites de mouvements jusqu’à ce nombre magique de (236 × n)¹¹. Si on n’a pas gagné d’ici-là, c’est maintenant une preuve que le nœud n’est pas trivial et on peut s’arrêter. On dit maintenant que notre problème est calculable ou bien décidable.

Les exemples donnés plus haut par votre chat ont 11 croisements, ce qui donne une suite d’au-plus (236 × n)¹¹ = 3.6 × 10³⁷ mouvements. Ce nombre est fini, mais en effectuant mille millards d’opérations par seconde, il nous faudrait 3.6 x 10²⁵ secondes : on est déjà bien au-delà de l’âge de l’univers, qui est autour de 4.5 × 10¹⁷ secondes. Et pourtant, c’est un problème ouvert d’obtenir un meilleur nombre magique que ce (236 × n)¹¹. Pour ce problème, la meilleure borne inférieure connue est une famille de nœuds triviaux à n croisements construits par Joel Hass et Tahl Nowik, pour lesquels on peut prouver qu’il faut au moins 2 n² + 3 n − 2 mouvements de Reidemeister.

Polynômes et complexité

Du point de vue de l’informatique théorique (qui porte bien son nom), ce (236 × n)¹¹ n’est considéré pas si mal : certes cela donne des grands nombres, mais la croissance reste contrôlée puisqu’il s’agit d’un polynôme en n, ici de degré 11. D’autres fonctions croissent bien plus vite, comme les exponentielles, et il y a même pire.

Cependant une importante clarification s’impose : si le nombre de mouvements de Reidemeister a une taille polynomiale, encore faut-il les trouver. Et cette recherche de la bonne suite de mouvements aura une complexité (nombre d’opérations nécessaire) exponentielle. Existe-t-il un algorithme de complexité polynomiale pour démêler les nœuds triviaux ? C’est un des problèmes ouverts les plus importants du domaine. Le meilleur algorithme connu, annoncé par Marc Lackenby en 2021 a une complexité quasi-polynomiale.

Cette situation, où un problème admet une solution de taille polynomiale si elle existe mais il n’est pas facile de la trouver, est très commune en informatique : on parle de problèmes dans la classe de complexité NP. Nous renvoyons à un autre article Interstices pour une introduction au domaine fascinant de la complexité algorithmique et le million de dollars à la clé. En termes pratiques, les problèmes NP sont considérés difficiles à résoudre, mais il est facile de vérifier une solution quand elle est donnée. Vous pouvez ainsi vérifier par vous-même que le nœud de droite était trivial en suivant mes gribouillages. 

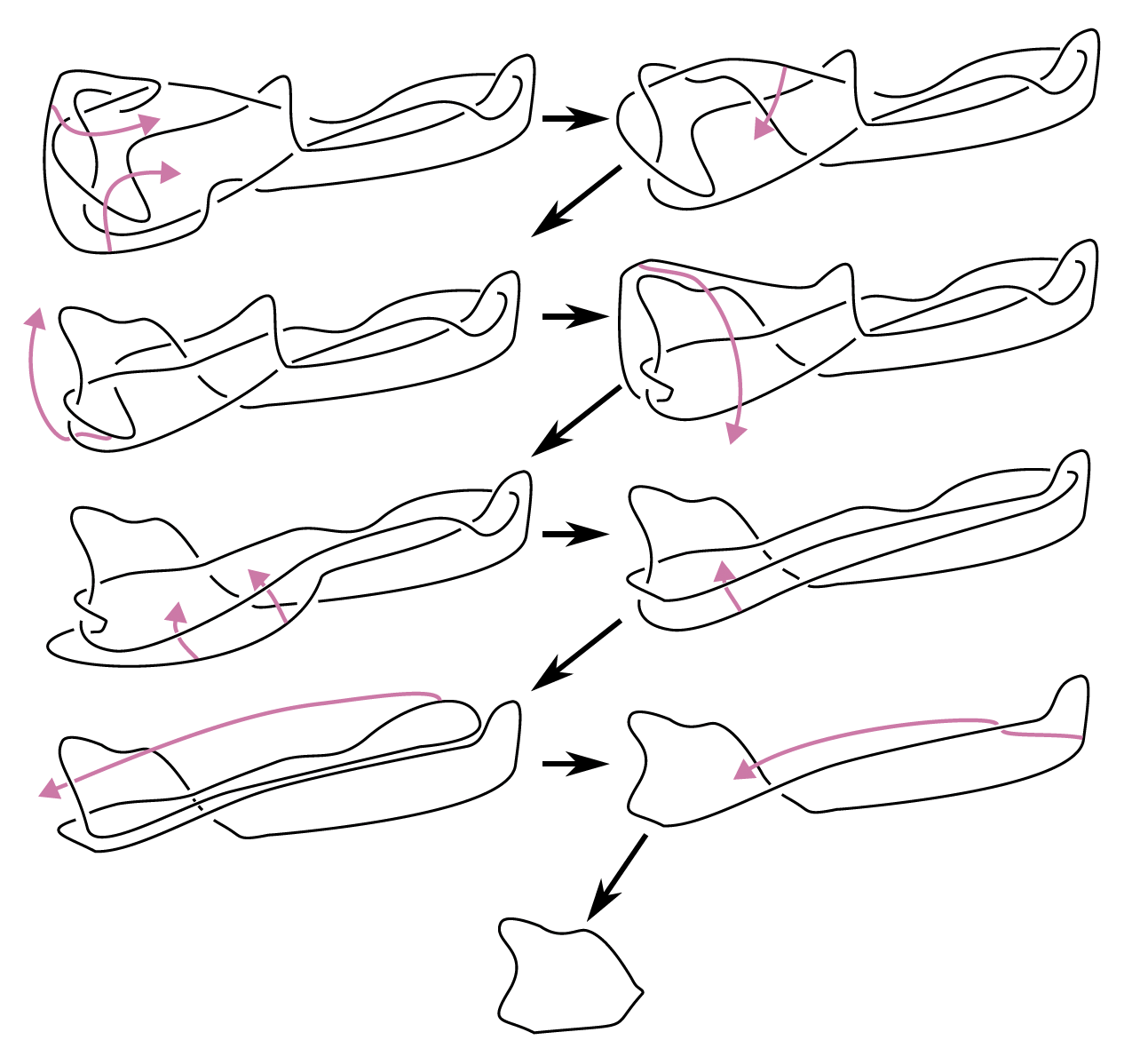
Le problème inverse

Mais qu’en est-il de l’exemple de gauche ? Vous l’aurez deviné, celui-là n’est pas trivial, mais comment puis-je vous en convaincre ? Sauf à essayer toutes les suites de (236 × n)¹¹ mouvements de Reidemeister, cela nécessite une autre approche. Une façon de faire est d’utiliser un invariant : une propriété d’un nœud qui reste valide pour tous ses diagrammes. L’exemple le plus simple est la tricolorabilité : on dit qu’un nœud est tricoloriable si on peut colorier ses brins en exactement trois couleurs, avec les contraintes suivantes :

• on n’a le droit de changer de couleur que lorsque l’on passe sous un croisement, et
• à chaque croisement, on voit soit exactement trois couleurs, soit une seule.

Figure 2 — Tricoloriage : à gauche, trois couleurs se retrouvent à un croisement, au milieu, une seule couleur et à droite un nœud de trèfle est tricolorié.

On peut prouver que cette mystérieuse propriété de tricolorabilité est un invariant : si deux nœuds sont équivalents, soit ils la satisfont toutes les deux, soit aucun ne la satisfait (le lecteur curieux peut d’ailleurs prouver cette invariance : il suffit de prouver que la propriété est maintenue lorsqu’on applique des mouvements de Reidemeister).

Il est immédiat de voir que le nœud trivial n’est pas tricoloriable : comme il n’y a pas de croisements dans le diagramme trivial, on ne peut pas le colorier avec trois couleurs. Pour certifier qu’un nœud est non-trivial, il suffit donc d’exhiber un tricoloriage. Arriverez-vous à en trouver un pour l’exemple de gauche ? 

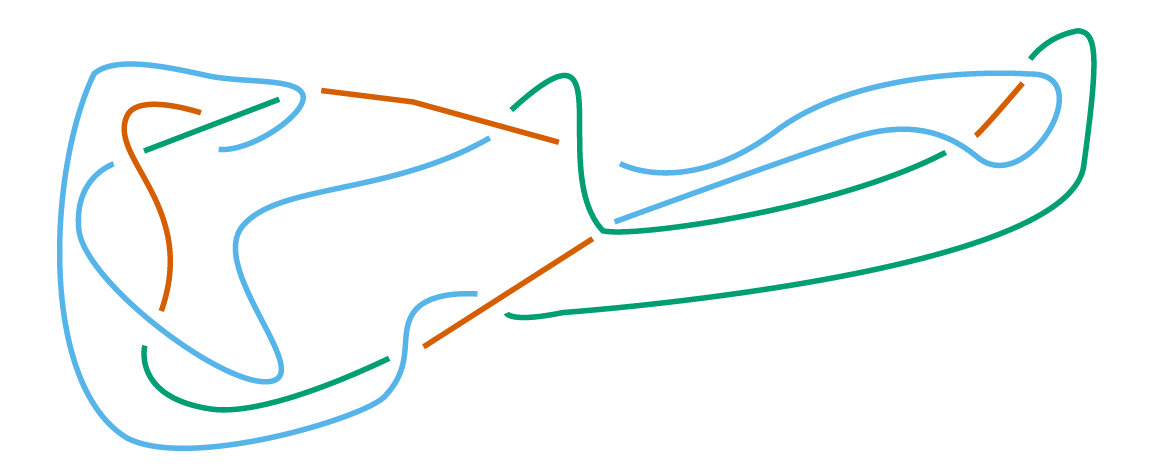
Un autre aspect de cet invariant est que l’exemple de droite n’était pas tricoloriable, puisque, comme on l’a vu c’est un nœud trivial déguisé. Vous pouvez essayer de vous en convaincre à la main, mais on se heurte dans ce cas à un problème très similaire au précédent : s’il est facile de vérifier un tricoloriage valable, pour se convaincre qu’il n’y en a pas, il faut les essayer tous.

Cette méthode a des limites et ne marche pas tout le temps : certains nœuds ne sont pas triviaux et ne peuvent cependant pas être tricoloriés. Mais en 2014, Greg Kuperberg a montré qu’une certaine généralisation de cette méthode fonctionne : il existe un invariant de taille polynomiale qui détecte tous les nœuds non triviaux. Il y a un hic cependant : la preuve de Greg Kuperberg suppose la véracité de l’Hypothèse de Riemann généralisée, une autre conjecture à un million de dollars ! Heureusement, des travaux plus récents ont montré comment obtenir des certificats de non-trivialité sans avoir besoin de cette hypothèse un peu audacieuse.

En termes informatiques, cela montre que notre problème est dans la classe de complexité co-NP. Comme il est également dans NP, il existe donc deux certificats, franchement différents, l’un pour certifier quand un nœud est trivial, et l’autre pour certifier quand il ne l’est pas. Une telle situation en l’absence d’un algorithme polynomial est très rare en informatique, ce qui motive la quête, très active depuis une vingtaine d’années, vers des algorithmes de plus en plus efficaces.

Pour aller plus loin 

Si cet article vous a intrigué, je vous recommande pour découvrir la théorie des nœuds la lecture de l’excellent et très accessible livre de Colin Adams, qui n’a hélas à ma connaissance pas été traduit en français.