La théorie de la complexité algorithmique pour calculer efficacement

De la calculabilité à la complexité

Figure 1. EDVAC, l’un des premiers ordinateurs électroniques, occupait 45,5 m² pour un poids de 7 850 kg mais sa mémoire n’était que de 5,5 kilooctets. Crédits : U.S. Army Photo / Public Domain via Wikimedia

C’est dans les années trente qu’Alan Turing, Alonzo Church et Kurt Gödel introduisent la notion de calcul, par l’intermédiaire, entre autres, de la machine de Turing, ancêtre abstrait de l’ordinateur. Les mathématiciens découvrent alors avec effroi que certains problèmes — comme celui de décider si un énoncé mathématique admet une preuve valide — ne sont pas calculables, c’est-à-dire qu’ils ne peuvent être résolus à l’aide d’un algorithme, anéantissant par là-même le projet de David Hilbert — identifié sous le nom de « problème de la décision » (Entscheidungsproblem) — d’automatiser la recherche de preuves mathématiques. Pourtant, dès les années soixante et avec l’utilisation de plus en plus récurrente des ordinateurs, le paradigme se met à évoluer. On réalise qu’en pratique, la plupart des problèmes que l’on veut résoudre s’avèrent être calculables. Rappelons qu’à l’époque, la vitesse des processeurs ainsi que la mémoire disponible sont très limitées (voir la figure 1 ci-contre à droite). Dès lors, la vraie question devient : peut-on trouver des méthodes de résolution efficaces ? Cette question est l’essence même de la théorie de la complexité, qui est l’art de déterminer ce que l’on peut résoudre en ayant une quantité donnée de ressources à disposition (temps, espace mémoire, etc). L’une des questions les plus connues posées par cette théorie, qui fait partie des « problèmes du prix du millénaire » de l’institut Clay, et dont la résolution vaut la coquette somme d’un million de dollars, est « P = NP ? ».

Pourquoi il est important de savoir qu’un problème est difficile à résoudre

Les recherches tournent autour de deux quêtes complémentaires. La première consiste à trouver les algorithmes les plus efficaces possibles pour résoudre un problème — c’est la quête dite des bornes supérieures. La deuxième, qui la complète, est de montrer qu’un algorithme est bien le meilleur, c’est la quête dite des bornes inférieures. En pratique, les choses sont plus nuancées. La meilleure borne inférieure connue n’est pas toujours la même que la meilleure borne supérieure connue ; on peut alors être tenté d’améliorer les algorithmes existants ou bien d’affiner la borne inférieure.

Pourquoi chercher des bornes inférieures ? Comprendre qu’un problème n’est pas efficacement soluble peut s’avérer d’une importance capitale pour plusieurs raisons. Un problème difficile peut être un gage de sécurité. Par exemple, le chiffrement RSA, très utilisé pour échanger de manière sécurisée des données, notamment sur Internet, repose sur l’hypothèse que factoriser un nombre en ses facteurs premiers est un problème difficile pour un ordinateur. Démontrer cette intuition nous permettrait de dormir sur nos deux oreilles. De plus, savoir qu’un problème est difficile nous évite de chercher inutilement des méthodes efficaces qui n’existent pas. À la place, il semble plus raisonnable de restreindre ses ambitions en recherchant, par exemple, des solutions approximatives.

Comptons les opérations élémentaires

Lors de l’exécution d’un algorithme, l’ordinateur effectue une succession d’opérations très simples comme comparer des petits nombres par exemple. On mesure alors la complexité en temps d’un algorithme comme le nombre de ces opérations élémentaires. Par exemple, en considérant élémentaire l’addition de 2 chiffres, poser l’addition de deux nombres de n chiffres nous fera effectuer n additions à 1 chiffre, la complexité sera donc de n. En revanche, poser la multiplication de ces deux même nombres (par la méthode apprise à l’école) aura une complexité de l’ordre de n². L’intérêt de ne compter que ces opérations (et pas le temps réel) est de s’affranchir de la puissance proprement dite de l’ordinateur. Un ordinateur récent sera vraiment beaucoup plus rapide que l’ordinateur laissé au placard depuis le début des années 2000, mais le nombre d’opérations élémentaires restera à peu près identique. De cette manière, on peut parler de complexité intrinsèque d’un problème : c’est le plus petit nombre d’opérations élémentaires nécessaires à un algorithme afin de résoudre ce problème.

Soulignons que la complexité possède de multiples aspects. On mesure le plus souvent la complexité dans le pire des cas, c’est-à-dire sur la pire instance du problème. Cependant, il sera parfois plus judicieux de mesurer la complexité en moyenne (c’est-à-dire la difficulté moyenne d’une instance prise au hasard). De même, plutôt que de s’intéresser au temps, on peut également considérer la complexité en espace (l’espace mémoire nécessaire pour résoudre le problème).

Classifier les problèmes : les classes de complexité

La théorie s’intéresse à comprendre comment va se comporter la complexité d’un problème en fonction de la taille de son entrée. L’objectif est de regrouper les problèmes de complexité similaire dans des catégories appelées classes de complexité. Par exemple, pour une fonction g(n), on définit la classe DTIME(g(n)) comme l’ensemble des problèmes que l’on peut résoudre en g(n) opérations élémentaires sur une entrée de taille n (pour des raisons techniques, les temps d’exécution sont en fait à considérer à une constante multiplicative près, mais nous ferons l’impasse sur ce détail !). Comme vu plus haut, additionner deux nombres de n chiffres se résout en temps n donc appartient à DTIME(n). On peut aussi montrer qu’on ne peut pas faire mieux ou, autrement dit, que ce problème n’appartient pas aux classes plus petites. Pour la multiplication, c’est plus délicat. Comme évoqué précédemment, elle peut s’effectuer en n² opérations et on pourrait s’imaginer que c’est optimal. Il n’en est rien : l’algorithme (non trivial) de Schönage-Strassen montre par exemple que ce problème peut se résoudre en temps n log(n) log log(n), ce qui est sensiblement mieux que n² ! Il existe une méthode plus abordable, l’algorithme de Karatsuba, beaucoup plus efficace que la méthode apprise à l’école mais toutefois moins efficace que celle de Schönage-Strassen.

En 1965, un des résultats fondateurs de la théorie voit le jour — le théorème de hiérarchie de Hartmanis et Stearns. Celui-ci explique l’adage suivant, intuitif mais toutefois loin d’être évident à prouver : « avoir plus de temps permet de résoudre strictement plus de problèmes ». Plus formellement, ce théorème montre qu’il existe des problèmes qui peuvent se résoudre en temps h(n) mais pas en temps g(n) dès lors que h(n) est sensiblement plus grand que g(n). Du point de vue des classes, ceci équivaut à dire que DTIME(g(n)) est strictement incluse dans DTIME(h(n)) si g(n) est beaucoup plus petit que h(n).

Un pied dans le bestiaire des classes de complexité

Il existe des centaines de classes de complexité capturant chacune un concept différent — l’intuition, la stratégie des jeux de plateau, le hasard, la communication, etc. Vous pouvez jeter un œil à l’excellent « Zoo de complexité » pour vous faire une idée (Diagramme des classes de complexité, Le site du Zoo).
Effleurons-en quelques-unes.
La classe P est l’ensemble des problèmes qui peuvent se résoudre en temps polynomial. Autrement dit, c’est la collection de tous les problèmes se résolvant en temps n^c, et ce pour n’importe quelle constante c. Comme mentionné plus haut, l‘addition et la multiplication sont d’ailleurs dans la classe P. On trouve les premières occurrences de cette classe dans la thèse de Cobham-Edmonds, qui part du postulat que cette classe correspond à l’ensemble des problèmes « faciles ». Par opposition, les problèmes nécessitant un temps exponentiel —  du type 2^nc— sont jugés difficiles car même le plus puissant des ordinateurs ne pourra jamais résoudre que de très petites instances de ces problèmes. On regroupe dans la classe dite EXP tous les problèmes qui peuvent se résoudre en temps exponentiel.

La classe NP correspond quant à elle aux problèmes pour lesquels les solutions sont faciles à vérifier (c’est-à-dire que la vérification d’une solution peut se faire en temps polynomial), bien que trouver une solution peut s’avérer très difficile. Pensez au sudoku : si je vous donne la solution d’une grille, il est aisé de vérifier que celle-ci est bien la bonne ; en revanche, il semble plus corsé de trouver la solution elle-même. De même, factoriser un nombre semble être une tâche difficile ; en revanche, étant donnée la factorisation, il est facile de vérifier que celle-ci est bien correcte. Ces deux problèmes sont donc dans NP. On peut montrer que P est incluse dans NP, elle-même incluse dans EXP. On peut également montrer que P est différente de EXP comme corollaire du théorème de hiérarchie de Hartmanis et Stearns. En revanche, la célèbre question « est-ce que P est égal à NP ? » reste ouverte et revient en fait à se demander : « trouver une solution est-il aussi facile que la vérifier ? ».

À première vue, on a l’impression que non. Résoudre un sudoku difficile nécessite souvent de tester énormément de possibilités à l’aveugle avant d’arriver à la solution. Pourtant, on ne sait pas le démontrer et cette question vaut un million de dollars !

Le temps n’est pas la seule ressource importante, on peut également s’intéresser à l’espace mémoire nécessaire (que l’on compte en termes de briques d’espaces élémentaires). Ainsi, PSPACE se définit comme l’ensemble des problèmes dont la résolution nécessite un espace mémoire polynomial. Il est peut-être surprenant de constater que l’espace mémoire semble être une ressource plus puissante que le temps puisque l’on peut montrer que cette classe se situe quelque part entre NP et EXP.

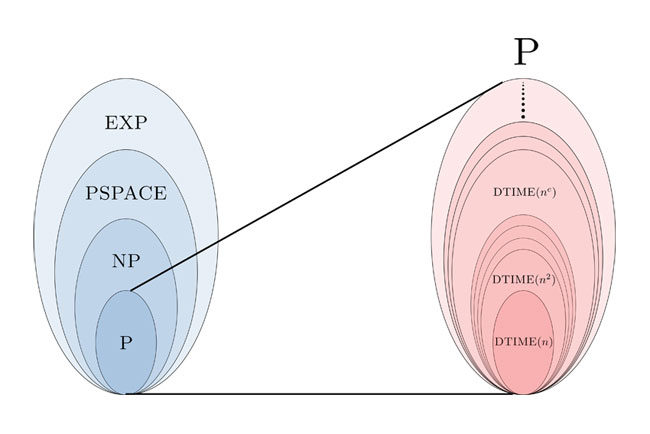
Figure 2. À gauche : imbrication des classes de complexité mentionnées. On ne sait ni démontrer que P ≠ NP, ni que NP ≠ PSPACE, ou encore que PSPACE ≠ EXP mais il est suspecté que ces inégalités soient vraies. À droite : zoom sur la classe P ; le théorème de hiérarchie dit que les sous-classes représentées sont d’inclusions strictes.

Complétude de classe

Il est possible de comparer les problèmes entres eux via la notion de réduction. Intuitivement, un problème A se réduit à un problème B si dès lors que l’on sait résoudre B alors on sait aussi résoudre A. Si tel est le cas, le problème A n’est alors pas plus difficile que le problème B. Par exemple, montrons qu’on peut réduire le problème de la multiplication de deux nombres au fait de savoir simultanément élever au carré, additionner et diviser par deux. Pour cela, remarquons que a×b = ((a+b)²−a²−b²)/2. Ainsi, pour calculer la multiplication de a par b, il suffit d’effectuer 3 additions, 3 élévations au carré, et une division par 2.

Le début des années 1970 est un tournant majeur de la théorie : Stephan Cook et Leonid Levin démontrent qu’un problème dénommé SAT est NP-complet, ce qui signifie que tous les problèmes de la classes NP se réduisent à SAT. Ainsi, si on sait résoudre ce problème particulier efficacement alors on sait également résoudre tous les autres problèmes de la classe NP au passage ! L’existence même d’un tel problème a un côté mystérieux et magique, et explique en partie l’importance pratique du problème SAT car de nombreux problèmes de la vie réelle se réduisent à celui-ci. D’ailleurs, chaque année est organisée une compétition internationale de solveurs SAT (site de la compétition) qui procure une émulation positive à la communauté. Très vite, on se rend compte que de nombreux problèmes s’avèrent aussi NP-complets : planifier des trajectoires, ordonnancer des ateliers de production, résoudre des sudokus, le problème du voyageur de commerce, n’en sont que quelques exemples. (cf ici pour une liste non exhaustive)

La notion de complétude n’est pas l’apanage de la classe NP et se révèle un outil précieux pour la compréhension de n’importe quelle classe de complexité. Trouver une stratégie gagnante pour le jeu mahjong, par exemple, est PSPACE-complet. Ainsi, savoir résoudre le mahjong permet en réalité de résoudre tous les problèmes de la classe PSPACE ! En revanche, le jeu de go semble être plus difficile puisqu’il se révèle être EXP-complet.

D’autres complexités

Les complexités sont dépendantes d’un modèle de calcul. Celui que nous avons considéré pour l’instant correspond à l’ordinateur classique. Il n’est pas impossible qu’un problème difficile pour ce modèle devienne facile dans un autre. En 1994, Peter Shor formule un algorithme quantique efficace de factorisation d’entiers. Ce problème, a priori difficile pour un ordinateur classique et sur lequel repose le système cryptographique RSA, s’avère donc facile pour un ordinateur quantique. L’étude de la complexité vis-à-vis du modèle quantique ouvre donc un nouveau champ des possibles dans ce domaine de la recherche et a amené à définir des classes de complexités… quantiques cette fois-ci ! On pourrait aussi considérer d’autres modèles comme l’ordinateur à ADN imaginé par Leonard Adleman, par exemple.

Enfin, comme mentionné précédemment, il n’est pas inutile de souligner que la théorie de la complexité s’intéresse le plus souvent à la complexité dans le pire cas, c’est-à-dire sur la pire instance du problème. En pratique, les instances que l’on veut réellement résoudre (c’est-à-dire celles issues du monde réel, provenant de l’industrie par exemple) sont très particulières et peuvent s’avérer faciles à résoudre, bien que le problème général, lui, soit difficile. Ainsi, une preuve de difficulté d’un problème ne justifie donc pas nécessairement l’arrêt de la recherche de méthodes efficaces pour les cas pratiques.