Des arithmétiques pour la géométrie
De nombreux algorithmes géométriques sont sensibles aux erreurs d’arrondis causées par l’arithmétique flottante des ordinateurs. Une analyse détaillée des raisons sous-jacentes à ces problèmes de non-robustesse peut être effectuée pour chaque algorithme, comme par exemple le calcul d’enveloppe convexe. Pour cet algorithme, des problèmes apparaissent lorsque des points sont presque alignés. Cet exemple est développé dans le document Un joli algorithme géométrique et ses vilains problèmes numériques.
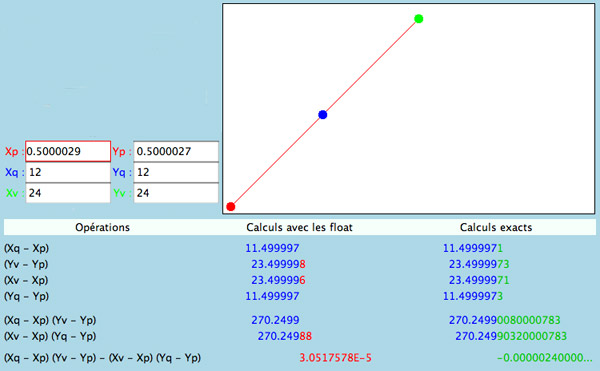
Exemple de problème rencontré lors du calcul d’enveloppe convexe.
Un algorithme géométrique se compose de propositions élémentaires appelées prédicats. Un prédicat est en fait l’équivalent d’une question dont la réponse peut être oui ou non. Cela revient à faire un calcul, et la proposition est vraie ou fausse selon que le résultat du calcul est positif ou négatif. Lorsqu’une erreur survient dans un prédicat, elle peut perturber l’algorithme dans sa globalité. En revanche, résoudre les problèmes au niveau des prédicats permet d’assurer la robustesse de l’algorithme.
Le paradigme du calcul géométrique exact
La première solution générale à avoir été utilisée pour résoudre ces problèmes a été de calculer les prédicats géométriques à l’aide d’une arithmétique exacte en lieu et place de l’arithmétique flottante fournie par les ordinateurs. Des entiers multiprécisions sont ainsi représentés en mémoire par un tableau de mots, et les opérations arithmétiques sont définies sur cette représentation. Cette représentation est étendue aux rationnels multiprécisions de manière évidente. Des bibliothèques comme GMP offrent ce type de fonctionnalités.
Le principal problème de cette approche est son manque d’efficacité en pratique : elle peut facilement causer un ralentissement d’un facteur 100 à 1000 sur le temps de calcul d’un algorithme géométrique. En effet, les prédicats sont parfois de très petites routines en termes de lignes de code, comme le prédicat d’orientation de 3 points dans le plan qui n’est composé que de 5 soustractions, 2 multiplications et une comparaison, mais ils sont appelés des millions de fois au cours de l’exécution d’un algorithme.
Le calcul géométrique exact filtré
On utilise maintenant un moyen d’accélérer les calculs, tout en garantissant les propriétés d’exactitude des prédicats géométriques. L’idée générale est de considérer l’expression d’un prédicat dans son ensemble, et non pas les opérations arithmétiques qui la composent. On part de l’observation que le calcul flottant fournit généralement un résultat exact à un prédicat, mais qu’il échoue dans de très rares cas. L’idée des filtres arithmétiques consiste donc à fournir, en plus de l’évaluation en calcul flottant, un certificat qui permet de dire si le signe de la valeur approchée est le même que celui de la valeur exacte, ou s’il ne sait pas. Dans les cas où il ne sait pas certifier, on fait alors appel au calcul multiprécision coûteux, mais on espère que ce ne sera pas très souvent, et que donc le temps de calcul moyen des prédicats ne sera pas trop affecté. Si le certificat est rapide à calculer en comparaison de l’évaluation flottante du prédicat, et qu’il est suffisamment précis dans le sens où il sait certifier souvent, alors on peut espérer que le temps de calcul global sera bon.
Le type de filtres le plus facile à mettre en œuvre utilise l’arithmétique d’intervalles.
Il arrive souvent que l’on ait besoin de représenter, non pas uniquement la valeur d’un nombre, mais également une incertitude autour de ce nombre. C’est le cas par exemple lorsque les nombres représentent des mesures de quantités physiques qui sont faites avec une certaine imprécision due aux appareils de mesure. On utilise alors souvent un couple de nombres pour représenter ces intervalles d’incertitude. L’intervalle x = [xinf ; xsup] signifie « tous les nombres compris entre xinf et xsup ».
On peut effectuer des opérations arithmétiques sur ces intervalles, comme sur les nombres réels. Par exemple, on définit l’addition de deux intervalles x + y comme étant l’intervalle [xinf +inf yinf ; xsup +sup ysup]. L’opération +inf (respectivement +sup) signifie l’addition des deux nombres, arrondie au nombre flottant représentable le plus proche dans la direction – ∞ (respectivement + ∞).
Les arrondis des opérations arithmétiques de base sont des propriétés fournies par le calcul flottant des ordinateurs, qui suivent la norme IEEE 754.
Ces arrondis permettent de conserver la propriété d’inclusion, qui est que pour tout couple de valeurs réelles dans les intervalles x et y, leur somme se trouve nécessairement dans l’intervalle résultat x + y.

Exemple d’addition d’intervalles.
Ici, on additionne les intervalles [-6 ; -4] et [4 ; 5]. Le résultat [-2 ; 1] contient 0, le signe en est donc indéterminé.
De manière similaire, on définit la soustraction, la multiplication (légèrement plus compliquée), la division, la racine carrée… Les comparaisons d’intervalles, contrairement aux comparaisons de nombres réels, admettent une valeur indéterminée lorsque des intervalles se chevauchent. Par exemple, la comparaison [1 ; 2] < [3 ; 4] est vraie, mais [1 ; 3] < [2 ; 4] est indéterminée, parce qu’on peut trouver des couples de valeurs réelles dans les deux intervalles pour lesquels la comparaison est soit vraie soit fausse.
L’arithmétique d’intervalles est utilisée dans de nombreux contextes, en particulier pour contrôler les erreurs d’arrondis causées par le calcul flottant des ordinateurs.
On peut la généraliser en utilisant d’autres types de nombres pour représenter les bornes des intervalles. Par exemple, en utilisant les nombres flottants multiprécisions de MPFR, on peut obtenir des intervalles beaucoup plus précis.
Plus d’informations en anglais sur le site Interval Computations.
Accès à la bibliothèque C++ Boost Interval (logiciel libre).
Voir aussi la vidéo Intervalles qui présente un exemple d’analyse par intervalles : la résolution d’un système d’équations à deux inconnues dans un intervalle donné.
Pour ce faire, on évalue le prédicat avec des intervalles, et si le signe de l’intervalle final n’est pas indéterminé (il ne contient pas zéro), alors on n’a pas à faire appel au calcul multiprécision. Ce type de filtre est très précis et fait partie de la classe des filtres dynamiques. Le temps de calcul d’un algorithme géométrique utilisant ce type de filtres est généralement environ 4 à 5 fois plus lent que lorsqu’on utilise du calcul flottant (non robuste), ce qui est nettement meilleur que du calcul multiprécision.
D’autres types de filtres existent, dits statiques, qui sont encore plus rapides, car ils reposent sur une analyse fine des expressions des prédicats et des propagations d’erreurs d’arrondis. Expliquer en détail leur fonctionnement demanderait de faire appel à des notions plus ardues. Ces filtres sont néanmoins moins précis, et sont donc généralement couplés à de l’arithmétique d’intervalles, formant ce que l’on appelle des filtres en cascade. On arrive ainsi à des temps de calcul seulement 25 % plus lents que du calcul flottant non certifié. Ce surcoût est variable, car il dépend par exemple du jeu de données sur lequel on applique l’algorithme : il peut contenir plus ou moins de cas qui posent problème, qui sont la cause de l’utilisation du calcul exact coûteux.
Le calcul utilisant des filtres est appelé calcul paresseux, parce qu’il essaie de n’évaluer que ce qui est nécessaire pour fournir le résultat voulu, en l’occurrence le signe d’une expression. On peut faire le parallèle avec l’effort nécessaire à l’Homme pour déterminer l’orientation de 3 points dessinés sur une feuille : si les points ne sont pas presque alignés, alors la tâche est facile. Par contre, si les points sont presque alignés, il faut faire l’effort de porter sa vision proche de l’axe d’alignement des points (ou d’utiliser une règle) pour déterminer le résultat.

Ces techniques de filtres sont diffusées comme logiciels libres disponibles dans la bibliothèque C++ d’algorithmes géométriques CGAL.
Recherches en cours autour des problèmes de non-robustesse des algorithmes géométriques
Les prédicats étudiés en ce moment portent sur les calculs sur les objets courbes, plutôt que simplement des points ou des droites. Ce sont par exemple des calculs mettant en jeu des arcs de cercles ou d’ellipses.
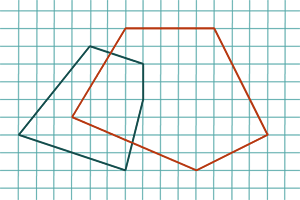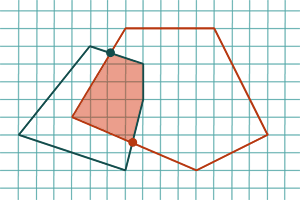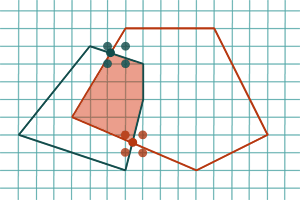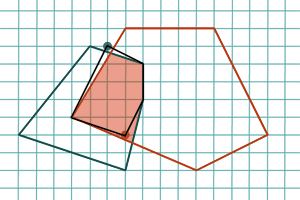
Comment arrondir les points d’intersection de deux polygones sur la grille des coordonnées flottantes ?
Ils font intervenir des techniques non seulement du domaine de l’arithmétique, mais également du domaine du calcul algébrique effectif, parce que des nombres algébriques (racines de polynômes) interviennent dans les calculs.
Un autre volet de recherche actuelle concerne l’accélération des calculs spécifiques aux constructions géométriques (par opposition aux prédicats bien mieux étudiés). Ce travail est également plus proche des applications, où la sortie des algorithmes est souvent contrainte à être dans un format donné. Par exemple, en CAO (Conception Assistée par Ordinateur), on calcule souvent des intersections de polygones dont les sommets ont des coordonnées flottantes, mais ceux du résultat sont en général rationnels. Il faut donc les reconvertir en nombres flottants. C’est le problème des arrondis géométriques, où la difficulté essentielle réside dans la conservation de propriétés géométriques d’une structure (par exemple la convexité).
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !
