Des outils mathématiques pour prévoir la fonte des calottes polaires

L’article Modéliser et simuler la fonte des calottes polaires décrit comment modéliser une calotte polaire pour simuler son évolution pendant une période donnée et pour faire des prédictions. En particulier, les simulations servent à estimer le volume de glace qui part dans l’océan sous forme d’icebergs et qui contribue à la montée du niveau des mers.

Ce deuxième article présente les outils mathématiques, que l’on appelle les méthodes inverses, qui permettent d’effectuer des prévisions fiables, en combinant deux sortes d’informations disponibles : le modèle d’évolution de la calotte polaire et les mesures physiques réalisées surtout à la surface du glacier.

Entrées et sorties du modèle

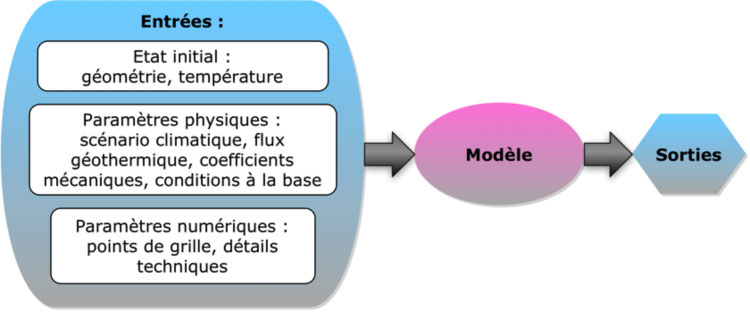
Le modèle mathématique traduit avec des équations les processus physiques en jeu dans le glacier. Ces équations sont transformées, pour pouvoir être résolues à l’aide d’algorithmes. Ceux-ci sont programmés dans un logiciel de simulation associé au modèle. Le modèle d’évolution d’une calotte polaire utilise des paramètres en entrée et fournit des résultats en sortie, selon le schéma suivant.

Les entrées du modèle sont des paramètres qui dépendent de la calotte polaire étudiée, du scénario climatique envisagé, etc. Ce sont des variables d’entrée dans le logiciel associé au modèle, dont les valeurs sont déterminées par les processus physiques ou choisies pour étudier divers scénarios. Voici une liste de quelques paramètres typiques d’un modèle de glacier.

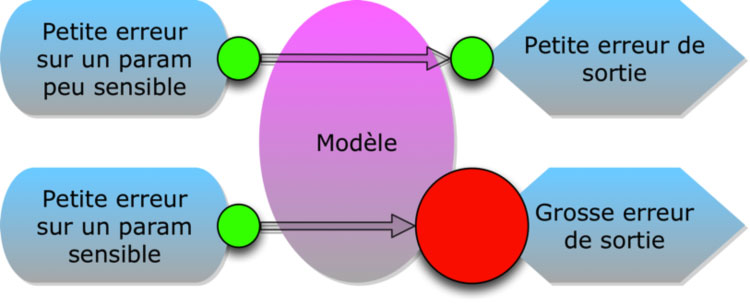
En pratique, les valeurs de ces paramètres sont entachées d’erreurs, qui vont se répercuter dans les équations du  modèle, s’influencer les unes les autres et finalement produire une erreur sur la sortie du modèle. Certains paramètres ont plus d’effet que d’autres sur l’erreur de sortie. Un paramètre est dit sensible si une petite erreur à l’entrée se traduit par une grosse erreur à la sortie ; il est dit  peu sensible si la petite erreur en entrée reste petite en sortie. Pour ces derniers paramètres, on n’a pas besoin d’être extrêmement précis, une bonne approximation suffit. Pour les paramètres sensibles en revanche, il est crucial de réduire l’erreur autant que possible, en vue d’effectuer des prévisions fiables du futur.

Les paramètres sensibles dans une calotte polaire

La perte de masse des calottes polaires par vêlage d’icebergs est contrôlée par un petit nombre de fleuves de glace ou glaciers émissaires, comme expliqué dans l’article Modéliser et simuler la fonte des calottes polaires. La présence ou non de fleuves de glace est intimement liée à la nature des conditions à la base de la calotte, qui permettent ou non un fort glissement et donc de grandes vitesses d’écoulement. En effet, si à la base de la glace se trouve de l’eau liquide, ou un sédiment gorgé d’eau, la vitesse pourra être grande, voire très grande (une dizaine de kilomètres par an).

Un autre paramètre essentiel est l’altitude du socle rocheux (toujours à la base de la calotte), notamment dans les zones côtières. En effet, la glace se déforme sous l’effet de son propre poids, qui est proportionnel à l’épaisseur de glace, donc à la différence entre l’altitude de surface et l’altitude du socle. De plus, la pression à la base de la calotte dépend aussi de l’épaisseur de glace.

Les conditions basales que sont le coefficient de frottement et l’altitude du socle sont effectivement des paramètres sensibles, car elles ont une forte influence sur l’écoulement : une petite variation de ces conditions basales provoque une grande variation de vitesse. Il est donc indispensable de les renseigner avec précision.

Or les observations pour les conditions de frottement à la base sont très limitées. En effet, il est quasiment impossible d’aller faire des mesures sous la glace, sauf en de rares points de forages profonds où le socle a été atteint. Les expériences en laboratoire sont assez peu représentatives, car il est impossible de restituer la pression équivalente à des milliers de mètres d’épaisseur de glace. D’autres incertitudes portent sur la nature rocheuse du socle et sur le flux géothermique qui conditionne la présence d’eau liquide. En pratique, on n’a donc pas de valeur précise du coefficient de frottement.

Pour la profondeur du socle, on dispose d’un nombre limité de mesures, faites par avion. Les fréquences radar qui permettent de mesurer l’altitude du socle rocheux à travers la glace sont des fréquences militaires, ce qui explique l’absence de mesures par satellite en Antarctique et au Groenland. Les observations sont ainsi restreintes à des traces de survol. En ces points de mesure, la précision est d’une vingtaine de mètres. Des méthodes mathématiques permettent d’estimer l’altitude dans les zones non observées mais l’incertitude peut alors atteindre plusieurs centaines de mètres. Les figures suivantes montrent l’état de l’art des cartes actuelles pour l’Antarctique.

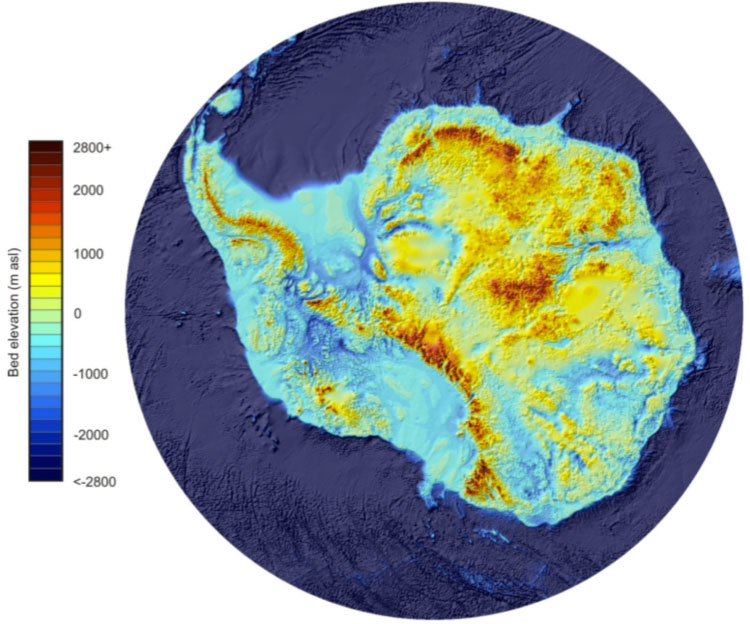
Carte d’observations de l’altitude du socle rocheux en Antarctique. Le plus haut sommet culmine à plus de 4500 mètres (en rouge, les zones de haute altitude). À cause du poids de la glace, de nombreuses régions sont situées environ 1000 mètres sous le niveau des mers (en bleu moyen sur le continent Antarctique). Cette carte, Bedmap2, a été obtenue à partir de mesures effectuées par avion en survol au-dessus du continent.

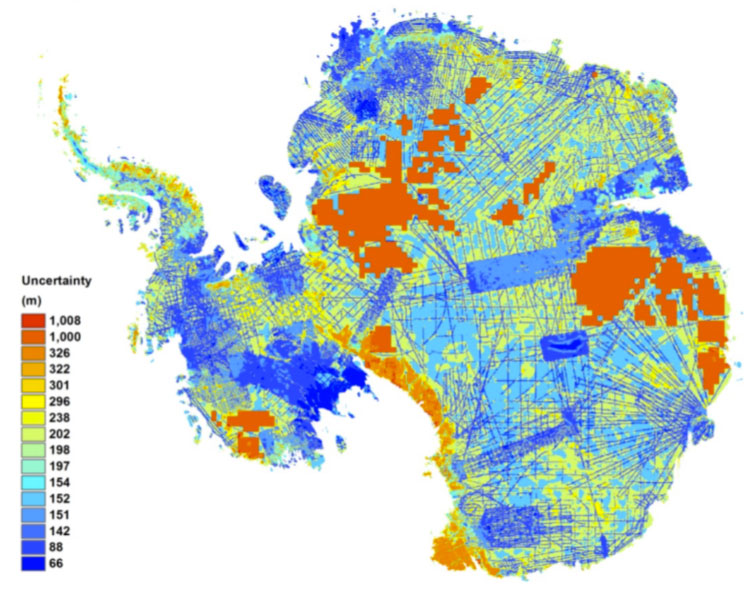
Carte des erreurs estimées pour les observations de l’altitude du socle rocheux en Antarctique. L’incertitude maximale atteint 1000 mètres dans les zones non observées, elle descend autour de 20 mètres au niveau des points de mesure, qui correspondent aux traces de survol par avion, qu’on voit clairement en bleu foncé sur cette carte.
Images : Fretwell, P. et al.: Bedmap2: improved ice bed, surface and thickness datasets for Antarctica, The Cryosphere, 7, 375-393, doi:10.5194/tc-7-375-2013, 2013.

Problème inverse

Les conditions basales que sont le coefficient de frottement et l’altitude du socle sont donc des paramètres à la fois sensibles et mal connus. Par contre, il est possible de disposer d’autres observations bien plus précises : des mesures par satellite fournissent l’altitude de la surface et la vitesse de la glace en surface. En remontant dans le passé, on dispose par exemple d’observations annuelles pendant une dizaine d’années. Peut-on utiliser ces observations pour en déduire les conditions basales ? L’idéal serait de pouvoir inverser le modèle, autrement dit de pouvoir calculer les paramètres du modèle à partir de ces observations.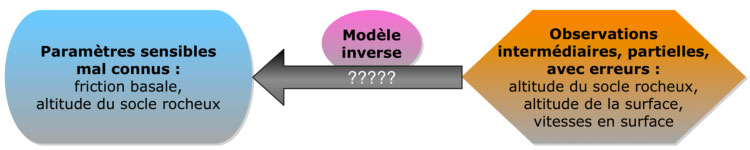

Malheureusement ce n’est pas aussi simple. Mathématiquement, on dit que le modèle « n’est pas inversible », ce qui veut dire qu’il n’y a pas de façon simple de passer des observations aux paramètres d’entrée inconnus.

Pour autant, les mathématiciens ont développé des « méthodes inverses », qui permettent malgré tout de répondre au problème, c’est-à-dire d’estimer au mieux les paramètres mal connus, en utilisant à la fois les observations et le modèle.

En effet, même si on ne peut pas écrire directement un « modèle inverse », on peut encore utiliser le modèle direct. En combinant les quelques observations et leur expertise, les glaciologues disposent d’une première estimation des paramètres d’entrée. L’idée est alors de fournir au modèle ces paramètres d’entrée « un peu faux » et d’exécuter le code associé pour obtenir des simulations qui vont du passé vers le présent.

Les sorties de ce modèle direct sont a priori inexactes, mais fournissent une altitude de surface et un champ de vitesses de surface que l’on peut comparer aux observations. La méthode consiste alors, grâce à l’écart entre les observations et les sorties simulées, à corriger les paramètres d’entrée, afin de réduire cet écart au minimum. Les paramètres qui minimisent l’écart sont la solution du problème inverse, ils expliquent au mieux les observations. Grâce à eux, on pourra effectuer des prédictions fiables pour le futur !

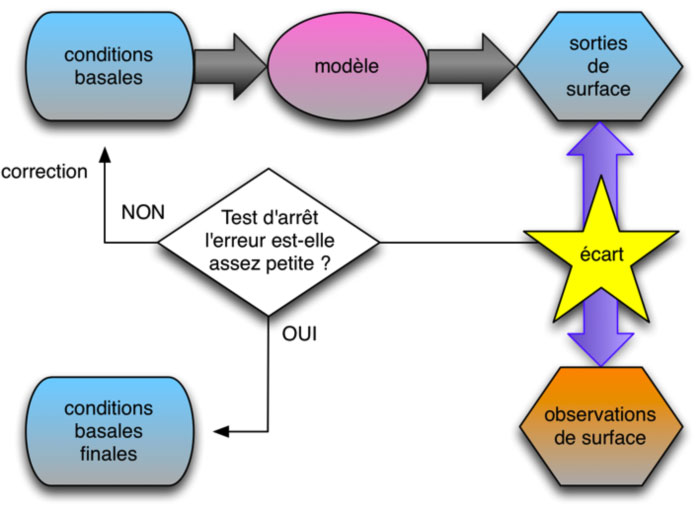
Algorithme de minimisation

Pour trouver les conditions basales qui minimisent l’écart entre valeurs observées et valeurs calculées, on utilise un algorithme itératif, qui procède par étapes successives. L’écart est réduit à chaque étape  et l’algorithme s’arrête lorsque l’écart est plus petit qu’un seuil, qui est un paramètre numérique fixé par les modélisateurs. L’algorithme se déroule selon le schéma suivant.

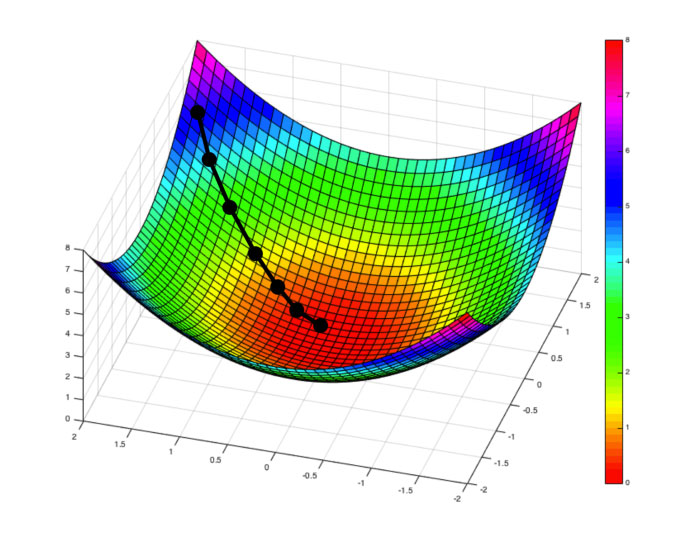
Pour réduire l’écart à chaque étape, on utilise une méthode dite « de descente ». Imaginons une randonneuse en montagne, qui souhaite descendre dans la vallée avec le moins d’étapes possible. Pour cela, elle descend étape par étape en suivant la ligne de plus grande pente pour corriger sa position. À chaque étape, elle recalcule sa position et la ligne de plus grande pente qu’elle emprunte pour effectuer son nouveau déplacement. Elle s’arrête lorsqu’elle est dans la vallée, autrement dit quand la pente est proche de zéro. On procède de façon similaire avec l’écart entre sorties et observations, qui correspond à l’altitude sur la montagne. On corrige les paramètres d’entrée (qui correspondent à la position sur la montagne) grâce à une ligne de plus grande pente, définie mathématiquement et calculée grâce au code associé au modèle direct.

Application au Groenland

Pour le Groenland, on dispose d’observations assez précises de l’altitude du socle. Le problème se résume alors à estimer le coefficient de frottement à la base. Les satellites RADARSAT ont fourni des observations pendant la première décennie des années 2000. La figure suivante montre un résultat obtenu par l’équipe  AIRSEA (Inria Grenoble Rhône-Alpes, Université Grenoble Alpes, Laboratoire Jean Kuntzmann), en collaboration avec des glaciologues du LGGE (Laboratoire de Glaciologie et de Géophysique de l’Environnement, Université Grenoble Alpes et CNRS), dans le cadre du projet ANR ADAGe. La résolution du problème inverse a permis d’obtenir un coefficient de frottement plus précis, et de faire des simulations à l’échelle du siècle pour estimer la contribution du Groenland à la montée du niveau des mers.

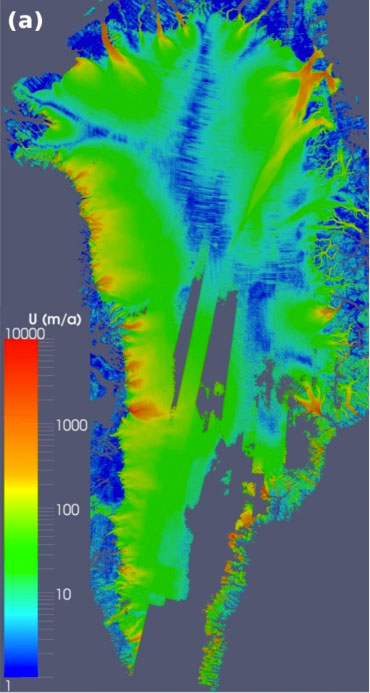
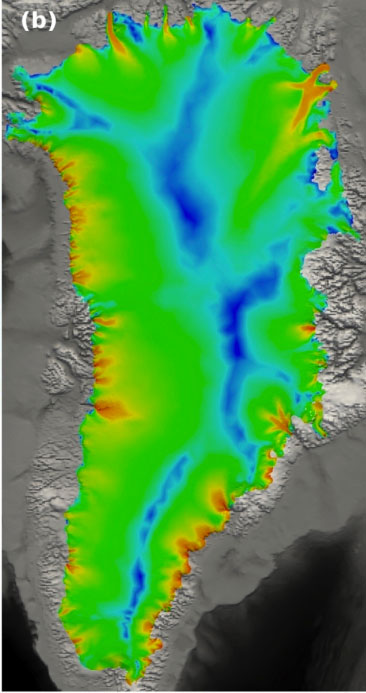
Vitesses à la surface du Groenland. À gauche (a), les vitesses observées par satellite. À droite (b), les vitesses reconstituées après détermination du coefficient de frottement basal. Les principaux glaciers émissaires (vitesses supérieures à 10 km/an) sont bien reproduits, l’écart entre observations et sorties a été minimisé.

Conclusion

Les méthodes inverses sont des outils puissants pour estimer l’état d’un système géophysique, en combinant l’information mathématique contenue dans les équations du modèle et l’information physique contenue dans les observations. Ces outils sont en particulier utilisées quotidiennement pour les prévisions météorologiques !

En glaciologie, il reste des incertitudes, dues au manque d’observations et à la complexité des processus physiques en jeu. À cause de cela, l’algorithme de minimisation nécessite parfois de nombreuses itérations donc un très long temps de calcul. Néanmoins, l’application des méthodes inverses en glaciologie a permis d’effectuer des prévisions fiables de la contribution des calottes polaires à la montée du niveau des mers, ce qui ouvre des perspectives intéressantes pour la prévision du changement climatique global.