
Genèse d’un algorithme
Cet article est devenu obsolète, de par son contenu ou sa forme, il est donc archivé.
Nous vous proposons de participer à la genèse d’un algorithme, de l’énoncé de la classe de problèmes qu’il est censé résoudre jusqu’à sa programmation et son test, en passant par sa formulation, puis sa formalisation.
1. Un problème simple
Nous considérons à cet effet un problème simple, dont l’intérêt scientifique ne saute sans doute pas aux yeux. Dans sa version la plus imagée, le problème consiste en effet à mettre dans l’ordre une pile de crêpes de différentes tailles. La crêpe de plus grand diamètre doit se retrouver en dessous de pile ; la plus petite au sommet ; entre les deux, toute crêpe doit reposer sur une crêpe plus large. Pour modifier l’arrangement de la pile de crêpes, vous êtes armé d’une spatule appropriée et contraint à un seul type d’action : insérer la spatule entre deux crêpes et retourner l’ensemble des crêpes du dessus.
Pour bien comprendre le problème posé, la première étape consiste, assez naturellement, à « jouer avec » et à chercher, en tâtonnant, des solutions dans les cas simples. Vous pouvez donc débuter votre apprentissage dans votre cuisine en confectionnant, par exemple, une pile de quatre ou cinq crêpes de tailles différentes. Vous testerez simultanément vos capacités physiques et intellectuelles en cherchant à les empiler par taille décroissante. Pour cela, vous devrez effectuer autant de fois que nécessaire l’opération qui consiste à placer la spatule sous une certaine crêpe judicieusement choisie et à retourner, en une seule action, l’ensemble des crêpes situées au-dessus de la spatule. Il est à parier que l’état de votre cuisine vous conduise très rapidement à reconnaître la nécessité d’abstraire le problème posé.
Il apparaît clairement que vous ne dénaturez pas le problème à résoudre en remplaçant les crêpes par des disques de carton, ou mieux encore des disques en bois, matière noble et nettement moins grasse que nos crêpes du début. Faut-il préciser que vous pouvez renoncer à l’usage de la spatule, si vous acceptez la règle qui consiste à ne retourner, en un seul mouvement, qu’un groupe de disques accessibles en sommet de pile ? Vous pouvez aussi, avantageusement et sans complexe, emprunter un des jeux dit d’éveil du petit dernier ou de la petite dernière de la famille.
Alternativement, vous pouvez monter d’un niveau dans l’abstraction du problème posé en vous essayant à le résoudre dans les différentes configurations que vous propose l’applet suivante. Comme le reste du monde, nos crêpes sont en passe de devenir numériques !
Pour accéder à l’applet Java, autorisez les applets du domaine https://interstices.info. Si votre navigateur n’accepte plus le plug-in Java, mais que Java est installé sur votre ordinateur, vous pouvez télécharger le fichier JNLP, enregistrez-le avant de l’ouvrir avec Java Web Start.
Applet réalisée par Régis Monte.
Alors, avez-vous réussi à identifier de façon systématique, à chaque étape, la crêpe en dessous de laquelle il vous faut placer votre spatule (virtuelle), de façon à arriver, en un nombre fini (s’il vous plaît…) d’actions, à remettre la pile dans l’ordre ?
Si oui, nous vous invitons à poursuivre votre lecture. Si non, continuez votre quête, honorable lecteur, et que l’inspiration soit avec vous.
2. Une démarche systématique
Bravo. De multiples essais, plus ou moins fructueux, vous ont donc permis de trouver une démarche systématique pour mettre dans l’ordre votre pile de crêpes ou équivalents.
Au tout début, vous choisissez la crêpe la plus grande, vous insérez votre spatule en dessous et vous retournez, en un mouvement, l’ensemble des crêpes situées au-dessus de la spatule. De ce fait, cette crêpe se retrouve maintenant au sommet de la pile. Il ne vous reste plus qu’à retourner la pile tout entière pour que la crêpe la plus grande soit désormais positionnée comme il faut. Bien entendu, si c’était le cas dès le début, il aurait été peu astucieux, car inutile, d’effectuer ces deux opérations de retournement.
Vous êtes désormais dans la situation où la crêpe à la base de la pile est à sa bonne place. Qu’elle y reste. Vous pouvez vous attaquer au reste de la pile. À cet instant, vous avez peut-être la sensation étrange d’un « déjà-vu ». Votre capacité d’abstraction, aiguisée par les exercices antérieurs, vous pousse à penser qu’en effet, en oubliant la crêpe désormais correctement positionnée, vous êtes face à la même situation qu’au début : il vous faut ordonner une pile de crêpes. La bonne nouvelle est que cette pile est plus petite ; le nombre de crêpes à ordonner a diminué de 1 par rapport au début.
On ne change pas une stratégie qui gagne. Vous identifiez, dans cette pile réduite donc, la crêpe la plus large ; vous retournez les crêpes de ce haut de pile ; enfin, vous retournez l’ensemble de la pile, sauf (faut-il vraiment vous le dire ?) la crêpe positionnée à l’étape précédente (on vous l’a dit, on n’y touche plus).
Deux crêpes sont maintenant correctement positionnées. Vous pouvez donc vous attaquer au reste de la pile, au-dessus de ces deux crêpes (non, vous ne touchez plus à ces deux crêpes !). Et recommencer : positionner la spatule, retourner le sommet de pile ainsi délimité, retourner la partie de la pile contenant les crêpes non encore triées, positionner la spatule, retourner le sommet de pile ainsi délimité, retourner la partie de la pile contenant les crêpes non encore triées, positionner la spatule…
Vous pouvez suivre l’exécution de l’algorithme à l’aide de l’applet suivante. Les différentes étapes de chaque cycle y sont détaillées.
Pour accéder à l’applet Java, autorisez les applets du domaine https://interstices.info. Si votre navigateur n’accepte plus le plug-in Java, mais que Java est installé sur votre ordinateur, vous pouvez télécharger le fichier JNLP, enregistrez-le avant de l’ouvrir avec Java Web Start.
Applet réalisée par Régis Monte.
Peut-être, à cette étape, êtes-vous pris d’une angoisse tout à fait légitime – bien des algorithmiciens l’ont connue : serez-vous un jour libéré de ce travail finalement peu valorisant et très répétitif qui consiste à trouver la bonne crêpe, effectuer deux opérations de retournement et recommencer avec le reste de la pile ? Autrement dit, arriverez-vous au bout de votre pile de crêpes ?
3. Des questions fondamentales
Pour répondre à votre angoisse, il y a une bonne et une mauvaise nouvelle. La bonne nouvelle, c’est que puisque la hauteur de votre pile de crêpes à ordonner se réduit de 1 à chaque étape, vous allez vous trouver à un certain moment face à une pile de hauteur 3, puis 2, puis 1. Celle-ci n’a évidemment pas besoin d’être ordonnée, puisqu’elle se réduit à une seule crêpe. Votre travail est fini.
La mauvaise nouvelle, c’est qu’il n’y a aucune raison, dans ce monde réel et cruel, que votre pile initiale ne comporte que 4, 5 ou 6 crêpes. Dans le monde numérique, on a vu des piles de très grande taille. Sans vouloir vraiment vous faire peur, rien n’empêche d’imaginer des piles de 109 crêpes (ou de n’importe quoi d’autre d’ailleurs). 109, c’est un milliard, autrement dit mille millions. Imaginez que, d’une sagacité et d’une dextérité sans pareilles, vous soyez capable en une seconde 1) d’identifier la bonne crêpe, 2) de retourner le sommet de pile ainsi défini, 3) de retourner la pile en cours de réordonnancement pour placer la bonne crêpe à sa bonne place. Il vous faudra donc un milliard de secondes pour arriver au bout du problème, et un milliard de secondes, mine de rien, ça fait environ 278 000 heures, soit 11 500 jours, soit près de 32 ans (à quelques jours près, d’accord).
Face à cette perspective vertigineuse, vous cherchez probablement à vous rassurer. Après tout, pensez-vous, à chaque étape, la pile à explorer pour trouver la bonne crêpe diminue d’une unité. Du coup, la recherche de la bonne crêpe devrait prendre moins de temps. Ce n’est pas faux et nous reviendrons sur ce point prochainement. Néanmoins, vous vous étiez engagés à faire les trois opérations de chaque étape en une seconde… Vous n’allez pas nous faire croire que vous pouvez faire mieux, même si la taille du sous-problème à résoudre se réduit à chaque étape.
De plus, juste pour alimenter sadiquement votre angoisse, qu’est-ce qui vous assure que lorsque l’algorithme s’arrêtera, la pile de crêpes sera dans le bon ordre ? Certes, vous avez vérifié que votre démarche donnait le bon résultat sur des piles de 5, 10, voire 30 crêpes. Mais comment être sûr qu’elle donnera le bon résultat sur des piles de 109 crêpes ?
L’algorithme finit-il ? Est-il performant ? Est-il correct ? Trois questions fondamentales qui ne peuvent trouver de vraies réponses par des essais sur des exemples, quels qu’ils soient et aussi nombreux soient-ils. Trois questions qui nécessitent de ce fait le recours à des techniques formelles que nous esquisserons plus loin.
À ce stade, restons positifs. Vous êtes parvenus à définir une démarche systématique qui conduit, en un nombre fini d’étapes, à résoudre le problème posé ; en un mot, vous avez défini un algorithme ! Et tout l’intérêt de concevoir un algorithme, c’est d’en confier l’exécution à un ordinateur. Cependant, nous nous sommes contentés jusqu’ici d’énoncer une description en langage naturel, insuffisamment spécifiée pour qu’une machine puisse l’interpréter. Il nous faut écrire notre algorithme dans un langage interprétable par une machine, ce que l’on appelle un langage de programmation. Or, il existe de très nombreux langages de programmation, et avant d’en choisir un, il est préférable de poursuivre la description de notre algorithme, en le précisant jusqu’au point où il pourra être décrit sans ambiguïté.

© nerate – Fotolia.
Simplifions-nous d’abord le problème. Il s’agit au départ d’ordonner une pile de crêpes. Vous avez progressivement accepté l’idée que les crêpes pouvaient être remplacées par des disques de carton, de bois ou de plastique (avez-vous testé un jeu d’éveil ?), sans que la nature du problème en soit affectée. Vous avez même joué avec ces « crêpes » stylisées à l’écran. Résoudre le problème des crêpes ne requiert donc pas de doter l’ordinateur d’un bras et d’une main et de lui ordonner de manier la spatule à bon escient. Nous nous contenterons de lui fournir et de lui faire exécuter un programme qui prenne en entrée une description de la pile et restitue en sortie la pile ordonnée.
Comment fournir cette description de la pile de départ ? Nous vous invitons ainsi à déterminer un codage adéquat d’une pile de crêpes, de telle sorte que cette description formelle puisse être manipulée par l’algorithme dûment formalisé, et ultérieurement par un programme.
4. Une description formelle
Notons N le nombre de crêpes de la pile (N est un nombre entier). À chaque crêpe, nous associons un nombre en fonction de sa taille. Le principe est qu’une crêpe plus grande qu’une autre se voit attribuer un nombre plus grand que celui attribué à cette dernière. Nous pouvons noter tout simplement le diamètre de chaque crêpe exprimé en millimètres, tel qu’il est possible d’en prendre la mesure à l’aide d’un double-décimètre.
Par exemple, une pile non ordonnée de 5 crêpes pourrait être visuellement représentée par le schéma ci-dessous.
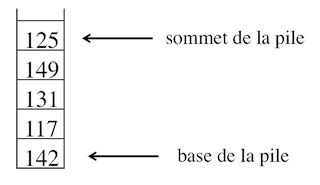

Des contraintes d’édition nous poussent à « renverser » la pile et à la noter simplement 125 149 131 117 142] dans la suite du texte : le nombre 125 est au sommet, placé juste « au-dessus » du nombre 149, qui lui-même est au-dessus du nombre 131, etc. Le caractère « ] » indique ainsi le « fond » de la pile. Une fois ordonnée, la pile se notera 117 125 131 142 149].
Notre algorithme prend en entrée la pile P et doit produire en sortie la pile P ordonnée. Exprimé sous cette forme, il s’agit d’effectuer un tri, procédure pour laquelle il existe de très nombreux algorithmes efficaces. La particularité ici est qu’une seule opération est admissible pour modifier l’ordre des éléments de notre pile : « retourner » une pile partielle constituée d’éléments situés au-dessus d’une certaine position.
Nous disposons de tous les éléments pour décrire le premier pas de l’algorithme. La première étape consiste à marquer l’endroit de la pile qui délimite la sous-pile à retourner. Pour revenir à nos crêpes de départ, il s’agit de déterminer l’endroit où nous insérons notre spatule. À ce stade de formalisation, nous supposons que nous disposons d’une fonction qui prend en entrée notre pile et une position K, et renvoie le rang du plus grand élément situé dans la pile au-dessus de la position K. Nous appelons PlusGrandElément cette fonction. Appliquée à la pile 125 149 131 117 142] et à la position 5, PlusGrandElément renverrait le rang du nombre 149 dans la pile, c’est-à-dire 2, puisque 149 est en 2e position dans la pile 125 149 131 117 142]. Appliquée à la pile 142 117 131 125 149] et à la position K = 4, PlusGrandElément renverrait le rang 1 du plus grand élément (142) de la pile parmi ceux situés au-dessus de l’élément en position 4.
Il reste à décrire les deux opérations de retournement : la première pour amener le plus grand élément de la liste au sommet de pile, la seconde pour retourner l’ensemble de la pile ainsi modifiée et positionner de fait le plus grand élément à sa base.
Là encore, nous supposons disposer d’une fonction, que nous appelons Retourner, qui s’applique sur une pile et une position, et renvoie comme résultat la pile obtenue en retournant la pile partielle constituée des éléments situés à partir de cette position.
Notre algorithme se ramène alors à la double application de la fonction Retourner. La première application permet d’obtenir, à partir de P, la pile P1 où le plus grand élément de P figure maintenant au sommet.
P1 ← Retourner (P, PlusGrandElément (P, N))
où N est la taille de la pile et ← se lit « prend la valeur ».
À cette étape donc, le plus grand élément se retrouve en sommet de pile P1. Ainsi, appliqué à la pile 125 149 131 117 142] et avec N = 5, ce premier appel à Retourner renvoie la pile 149 125 131 117 142].
La seconde application retourne la pile P1 à partir de sa base (la position numéro N de la pile) de telle sorte que le plus grand élément se retrouve désormais à la base de la pile résultante P2 :
P2 ← Retourner (P1, N)
Ce second appel à Retourner appliqué sur la pile 149 125 131 117 142], et toujours avec N = 5, renvoie la pile 142 117 131 125 149].
Il suffit d’ajouter P ← P2, pour que P soit la nouvelle pile dans laquelle l’élément situé à sa base est correctement positionné et ne doit plus être déplacé :
P1 ← Retourner (P, PlusGrandElément (P, N))
P2 ← Retourner (P1, N)
P ← P2
Très bien, direz-vous, nous avons bien placé à la base de la pile l’élément de plus grande valeur, mais comment fait-on pour le reste de la pile ? Eh bien, il suffit, comme nous l’avons vu plus haut, d’appliquer le même enchaînement de la fonction de retournement, mais à la pile privée de cet élément correctement placé à sa base, ici la pile 142 117 131 125 ], de taille 4. Il faut donc appliquer à nouveau les deux étapes précédentes, mais en ayant au préalable fait progresser d’une position en direction du sommet la marque de la base qui délimite la partie de la pile non encore correctement ordonnée, autrement dit diminuer N de 1.
Nous pouvons donc définir la fonction OrdonnerPile qui prend en entrée une pile P et un argument K, effectue l’enchaînement des retournements nécessaires pour obtenir le résultat souhaité à partir de la marque K, et renvoie ce résultat comme valeur de la fonction.
OrdonnerPile (P, K)
Si K > 1
P1 ← Retourner (P, PlusGrandElément (P, K)), K)
P2 ← Retourner (P1, K)
P ← OrdonnerPile (P2, K-1)
Sinon
P
ou dans un style purement fonctionnel :
OrdonnerPile (P, K)
Si K > 1
Soit P2 = Retourner (Retourner (P, PlusGrandElément (P, K)), K)
Dans OrdonnerPile (P2, K-1)
Sinon
P
La fonction OrdonnerPile est dite « récursive », car elle s’appelle elle-même lors de son déroulement. L’appel à OrdonnerPile au sein de la fonction OrdonnerPile est l’expression très naturelle, quoique déconcertante au premier abord, de l’algorithme : ordonner la pile consiste à placer un premier élément à sa base puis à réappliquer la même démarche au reste de la pile. Le test « K > 1 » traite le cas élémentaire où la pile est réduite à un seul élément et interdit que cette récursion se poursuive sans fin.
Pour trier la pile P, de taille N, il suffit donc tout simplement de calculer la fonction OrdonnerPile (P, N).
5. Un programme à exécuter, à vérifier, à améliorer…
Le calcul de la fonction OrdonnerPile peut être effectué par un ordinateur, et c’est évidemment tout l’intérêt d’avoir formalisé l’algorithme jusqu’à pouvoir l’écrire dans un langage de programmation. Un langage fonctionnel de type Caml peut servir à la rédaction d’un tel programme.
« C’est un peu court ! » pensez-vous à ce point de votre lecture. « Qu’en est-il des fonctions PlusGrandElément et Retourner ? ». Il est vrai qu’il faut évidemment les spécifier et les écrire elles aussi dans le langage de programmation choisi. Mais cette écriture ne présente pas de difficultés particulières. Aussi, nous vous la laissons volontiers comme exercice, non sans vous offrir un « corrigé » complet en langage Caml.
Voici le programme ordonne_pile.ml, écrit en langage Caml, qui implémente l’algorithme décrit.
(****** Affichage d'une pile ******)
(******une pile est représentée par une liste
dont le premier élément représente le sommet*****)
(*****[3;1;5;4;2] sera affichée comme:
3
1
5
4
2
********)
let rec affiche p = match p with
| [] -> print_string " "; print_newline()
| a::b -> ( print_int a; print_newline(); affiche b )
;;
(****** Retournement d'une pile ******)
let rec inverse p = match p with
| [] -> []
| a::b -> (inverse b)@[a]
;;
(****** Retournement d'une pile p à partir d'une certaine position n ******)
(*On partage d'abord la pile en 2 en fonction de la position n *)
let rec split p n =
if n = 0 then ([], p)
else let (p1,p2) = (split (tl p) (n-1)) in ((hd p)::p1 , p2)
;;
(* on inverse la partie au début
(qui représente la partie de la pile au dessus de la position n)
et on concatène le résultat avec l'autre partie de la pile restée inchangée *)
let Retourner p n =
if n = 1 then p else let (p1,p2) = split p n in (inverse p1)@p2
;;
(****** Recherche du rang du plus grand élément d'une pile
à partir d'une certaine position******)
(* on cherche d'abord le maximum et son rang dans une pile *)
let rec RangMax p = match p with
| [a] -> (a,1)
| a::b -> let m,r = RangMax b in if a > m then (a,1) else (m,r+1)
;;
(* on cherche ensuite le rang du maximum
dans la partie de la pile "au dessus" de la position k *)
let PlusGrandElement p k =
let (p1,p2) = split p k in (snd (RangMax p1))
;;
(****** Mettre dans l'ordre une pile par retournements
avec affichage du résultat des retournements ******)
let rec OrdonnerPileRec p k =
if k = 1 then p
else let p1 = Retourner p (PlusGrandElement p k) in
affiche p1 ;
let p2 = (Retourner p1 k) in
affiche p2 ;
OrdonnerPileRec p2 (k-1)
;;
let OrdonnerPile p = affiche p ; OrdonnerPileRec p (list_length p)
;;
OrdonnerPile [3;1;5;4;2]
;;
Voici une trace d’exécution de ce programme, qui montre les étapes successives.
> Caml Light version 0.74 #load "D:/Mon_ordi/interstices/ordonne_pile.ml";; affiche : int list -> unit = inverse : 'a list -> 'a list = split : 'a list -> int -> 'a list * 'a list = Retourner : 'a list -> int -> 'a list = Fichier "D:/Mon_ordi/interstices/ordonne_pile.ml", lignes 42-44, caractères 20-115: >....................match p with > | [a] -> (a,1) > | a::b -> let m,r = RangMax b in if a > m then (a,1) else (m,r+1) Attention: ce filtrage n'est pas exhaustif. RangMax : 'a list -> 'a * int = PlusGrandElement : 'a list -> int -> int = OrdonnerPileRec : int list -> int -> int list = OrdonnerPile : int list -> int list = 3 1 5 4 2 5 1 3 4 2 2 4 3 1 5 4 2 3 1 5 1 3 2 4 5 3 1 2 4 5 2 1 3 4 5 2 1 3 4 5 1 2 3 4 5 - : int list = [1; 2; 3; 4; 5] - : unit = () #
Remarquez que l’exemple traité par ce programme Caml utilise une représentation de la pile encore plus détachée de notre exemple d’origine. En effet, plutôt que de noter la mesure des diamètres des objets empilés, nous pouvons attribuer l’entier 1 à la plus petite mesure et l’entier N à la plus grande, et affecter les nombres 2 à N-1 selon ce principe. Une liste de N nombres compris entre 1 et N décrira ainsi une pile, de son sommet à sa base. Pour reprendre l’exemple traité ci-dessus, la pile à trier se note alors 2 5 3 1 4].
Comment s’assurer que notre algorithme, et la fonction OrdonnerPile dans laquelle il s’incarne, est correct, autrement dit qu’il trie bien les éléments de la pile donnée en entrée ? Une première approche consiste à exécuter « à la main » les opérations décrites dans le programme correspondant. Ainsi peut-on établir la suite des différentes piles obtenues lors de l’exécution de la fonction OrdonnerPile (2 5 3 1 4], 5). Évidemment, cette vérification ne peut raisonnablement se faire que sur des piles de petite taille, pour des raisons de temps, mais aussi à cause du risque accru d’erreur de vérification sur des exemples trop grands et donc très longs à « exécuter » : si le résultat obtenu « à la main » n’est pas le bon, est-ce dû au programme ou à l’humain (que vous êtes, cher lecteur) qui a (mal) suivi le programme ?

© pixarno – Fotolia.
S’il ne s’agissait que de trier des crêpes, la vérification de ce programme ne nous inquiéterait pas outre mesure. Mais si notre programme s’insère dans un ensemble dont la bonne exécution est critique ? On pense évidemment aux logiciels embarqués, dans des avions, des voitures, ou, dans une moindre mesure certes, des lave-linge (votre joli pull en cachemire lavé à 90° et essoré à 800 tours/minute, c’est pas critique ?). Plus généralement, confier des tâches à des ordinateurs requiert qu’elles soient correctement exécutées. Il faut donc, non pas simplement « montrer » que le programme produit des résultats corrects sur quelques (petits) exemples, mais « prouver » qu’il est correct. La preuve d’algorithmes est ainsi devenue un chapitre très important de l’algorithmique.
La deuxième préoccupation lors de la conception d’un algorithme et de sa réalisation sous forme d’un programme concerne son efficacité. Une solution simple est de mesurer le temps de l’exécution du programme sur des jeux de données différents, ici des piles plus ou moins ordonnées et de tailles différentes. La limitation essentielle de cette démarche empirique est que les temps d’exécution mesurés dépendent à l’évidence de l’ordinateur employé et des performances de son ou ses processeurs.
Les informaticiens cherchent donc plutôt à faire des estimations théoriques du nombre d’opérations élémentaires effectuées lors de l’exécution de l’algorithme, estimations indépendantes de l’implémentation de l’algorithme et de la machine qui l’exécute.
En ce qui nous concerne ici, les opérations élémentaires sont celles que vous vous êtes engagés à faire en une seconde, à savoir PlusGrandElément et Retourner. Le nombre d’opérations élémentaires dépend de la taille N de la pile. Il s’agit donc de la valeur d’une fonction C qui vérifie les équations :
(a) C (1) = 0
(b) pour N > 1 : C (N) = 3 + C (N-1)
En effet, dans le cas (a), si la pile se réduit à un seul élément, il n’y a aucune opération à faire. Dans le cas général (b), où la pile est de taille N (N > 1), il faut effectuer une fois l’opération PlusGrandElément et deux fois l’opération Retourner pour amener à la base le plus grand élément. Le nombre d’opérations pour ordonner la pile complète est donc 3 plus le nombre C (N-1) des opérations nécessaires pour ordonner la pile privée de cet élément, c’est-à-dire la pile de taille N-1.
Par récurrence, on montre que C (N) = 3 N et que donc le temps d’exécution est proportionnel à la taille de la pile à ordonner ; on dit qu’il est de l’ordre de N et on note O (N). Cela signifie que si la taille de la pile double, le nombre d’opérations double. On parle de complexité linéaire. C’est une situation relativement favorable. Ainsi, une complexité quadratique, notée O (N2) se traduirait, dans la même situation de doublement de la taille des données, par un quadruplement du nombre d’opérations, et donc du temps d’exécution.
Il ne s’agit ici que d’une première approximation de la complexité de notre algorithme. On comprend bien en effet que le calcul de PlusGrandElément, par exemple, dépend lui-même de la taille de la pile, qui, nous l’avons vu, diminue de 1 à chaque cycle de l’algorithme.
Mais cette observation n’est pas véritablement à même de modifier notre analyse de complexité. En effet, si nous décidons de ne retenir comme opérations élémentaires que les retournements de sous-piles, nous obtenons facilement C(N) = 2 N, c’est-à-dire que la complexité est toujours en O(N) : si N double, le temps double. L’applet qui montre le déroulement de l’algorithme affiche d’ailleurs ce nombre de retournements et il est facile de vérifier que ce nombre est effectivement proche de 2 N, où N est le nombre d’éléments à trier.
Il est important de souligner que cette étude de complexité, exemplaire dans la démarche suivie, a retenu comme opérations élémentaires la recherche du plus grand élément et le retournement d’un sommet de pile. En fait, lors de l’analyse des algorithmes de tri, les opérations dénombrées sont de plus petit grain : les comparaisons et les échanges de valeur entre deux éléments de la liste à trier. Ainsi, les méthodes qui trient les éléments deux à deux nécessitent de comparer chacun des N éléments avec chacun des N-1 autres éléments et le nombre de comparaisons est alors de l’ordre de N2, noté O(N2). Les meilleures méthodes de tri ont, elles, une complexité de l’ordre de N log(N).
L’analyse de complexité est un chapitre très important de l’algorithmique, avec des questions théoriques encore non résolues, telles que « P = NP ? ».
Nous avons fait plusieurs fois allusion précédemment à la possibilité d’optimiser l’algorithme, en évitant d’effectuer des opérations inutiles. Prenons un exemple extrême, et supposons que la pile de départ soit déjà correctement triée. Dans sa version actuelle, l’algorithme effectuera néanmoins toutes les opérations de retournement, bien qu’elles soient clairement inutiles ici.
De façon générale, il s’agit de reconnaître quand une crêpe est déjà correctement positionnée. Ainsi, si le plus grand élément identifié est situé juste au dessus des éléments déjà triés, il est inutile d’y toucher. De plus, si le plus grand élément identifié est situé tout au sommet de la pile, un seul retournement est nécessaire pour l’amener à sa bonne place. Ces modifications peuvent être apportées au programme, dont les performances en moyenne s’amélioreront. Pour autant, la classe de complexité de l’algorithme n’en sera pas affectée, car l’estimation 3 N (ou 2 N) constitue un majorant du nombre d’opérations.
La dernière question que, cher lecteur, vous êtes en droit de vous poser est « Mais à quoi peut bien servir cet algorithme, à part bien ranger une pile de crêpes, évidemment ? ». Au-delà de son caractère pédagogique, il se trouve que cet algorithme est utilisé pour résoudre des problèmes de routage dans des réseaux de processeurs qui calculent en parallèle. Satisfait ?
Mais revenons à nos crêpes.
Exigeants sur la présentation de notre pile, nous nous sommes aperçus que chaque crêpe comportait un côté plus brûlé que l’autre et nous souhaitons modifier notre algorithme, et la représentation de nos crêpes, afin que, dans la pile triée, ce soit toujours la face moins brûlée qui apparaisse, autrement dit qui soit tournée vers le haut.
Bon courage !
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Marie-Christine Rousset
Professeur à l'Université Joseph Fourier (Grenoble 1), chercheuse en bases de données et représentation de connaissances.
