
Alignement optimal et comparaison de séquences génomiques et protéiques
1. Comparer des séquences
Qu’est-ce qu’une séquence ?
Une séquence génomique est l’enchaînement des nucléotides le long d’une macromolécule d’ADN. Elle peut être représentée par une chaîne de caractères utilisant l’alphabet des quatre lettres A, C, G et T, initiales des bases azotées – Adénine, Cytosine, Guanine et Thymine – qui distinguent les quatre types de nucléotides. C’est l’enchaînement des nucléotides au sein des régions codantes des gènes qui dicte la suite des acides aminés qui compose un polypeptide, dont le repliement et diverses modifications chimiques conduiront à une protéine fonctionnelle. Une séquence protéique est l’enchaînement des vingt types d’acides aminés le long d’un polypeptide ; cette séquence est classiquement représentée par une chaîne de caractères qui utilise un alphabet de vingt lettres.
Voici les vingt lettres utilisées pour représenter les acides aminés, et le nom de l’acide aminé associé à chacune de ces lettres :
A : Alanine
C : Cystéine
D : Acide aspartique
E : Acide glutamique
F : Phénylalanine
G : Glycine
H : Histidine
I : Isoleucine
K : Lysine
L : Leucine
M : Méthionine
N : Asparagine
P : Proline
Q : Glutamine
R : Arginine
S : Sérine
T : Thréonine
V : Valine
W : Tryptophane
Y : Tyrosine
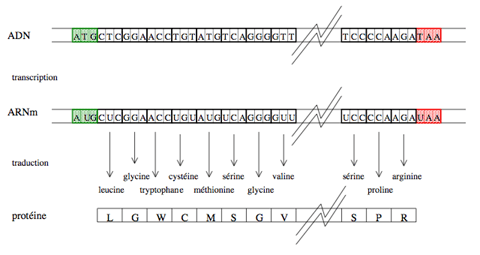
D’une séquence génomique à une séquence protéique.
Encadrée par les codons start (en vert) et stop (en rouge), la succession des codons d’une région codante d’un gène bactérien dicte, à travers les processus de transcription, puis de traduction via le code génétique, la composition de la protéine en acides aminés. L’orientation de la séquence de la gauche vers la droite correspond au sens de lecture du brin d’ADN. Le résultat de la transcription et de la traduction de la région codante est une séquence protéique, qui peut être vue comme un texte écrit dans un alphabet de 20 lettres.
La longueur de la séquence complète d’un génome bactérien est de l’ordre de 106 caractères ; celle d’un génome eucaryote est typiquement de deux ou trois ordres de grandeur plus longue. La longueur de la séquence d’un gène bactérien est de l’ordre de 103 caractères ; celle d’un gène eucaryote est supérieure d’un ordre de grandeur en moyenne, mais peut atteindre 106 caractères. Une séquence protéique comporte de l’ordre de 102 caractères.
Pourquoi comparer des séquences ?
La comparaison de séquences est de loin la tâche informatique la plus fréquemment exécutée par les biologistes. Il s’agit de déterminer dans quelle mesure deux séquences, génomiques ou protéiques, se ressemblent.
La motivation première est d’inférer des connaissances sur une séquence à partir des connaissances attachées à une autre. Ainsi, si deux séquences génomiques sont très similaires, et si l’une est connue pour être codante, l’hypothèse que la seconde le soit aussi peut être avancée. De même, si deux séquences protéiques sont similaires, il est souvent fait l’hypothèse que les protéines correspondantes assument des fonctions semblables ; si la fonction de l’une est connue, la fonction de la seconde peut ainsi s’en déduire. Ce principe d’inférence se justifie par des considérations sur le processus d’évolution qui seront expliquées plus bas.
Il existe des bases de données qui contiennent l’ensemble des séquences nucléiques publiques avec leurs annotations (par exemple GenBank), ou l’ensemble des séquences protéiques expertisées (SwissProt). Le premier réflexe d’un biologiste qui détient une séquence nouvelle est de parcourir ces bases de données, afin d’y trouver les séquences similaires et de faire hériter à la nouvelle séquence les connaissances qui leur sont associées.
C’est également en comparant des séquences de génomes d’espèces actuelles qu’il est possible de reconstruire des arbres phylogénétiques qui rendent compte de l’histoire évolutive.
Depuis son énoncé, la théorie de Darwin s’est progressivement imposée et il est à présent communément admis que tous les êtres vivants actuels descendent d’un ancêtre commun. Jusqu’aux années 1960, les travaux de classification tenant compte de l’histoire évolutive des espèces étaient limités à l’échelle « macroscopique » : comparer leurs morphologies, leurs comportements et leur distribution géographique. La découverte du support de l’hérédité puis de l’universalité du code génétique, et la disponibilité des séquences d’ADN et de protéines ont, dans ce domaine aussi, ouvert des perspectives nouvelles. C’est au niveau moléculaire que se recherchent à présent les « liens de parenté » unissant les différents organismes.
Pour cette recherche, les outils informatiques permettent une analyse des différents gènes d’un génome entier donné, ou bien l’étude de gènes homologues chez un très grand nombre d’organismes et d’espèces différentes. Dans tous les cas, des algorithmes de comparaison et d’alignement de séquences sont sollicités. Le principe est simple : il s’agit d’aligner plusieurs séquences codantes homologues, la « distance » entre ces séquences (c’est-à-dire leur degré de similitude) est alors proportionnelle à la distance relative des organismes correspondants sur l’arbre de vie.
Bien sûr, cette approche n’exclut pas les méthodes plus anciennes de phylogénie et vient compléter les enseignements apportés par des disciplines comme la paléontologie, l’éthologie ou des études d’embryogenèse.
Pourquoi existe-t-il des séquences similaires ?
Des facteurs multiples sont à l’origine de modifications de la séquence génomique : un nucléotide peut être substitué par un autre, disparaître ou au contraire s’insérer. Ces erreurs et ces mutations sont susceptibles de se propager au sein des populations. Ainsi, la séquence d’un génome d’une espèce, c’est-à-dire l’enchaînement des nucléotides qui composent les macromolécules d’ADN au sein de ses chromosomes, évolue dans le temps.
L’histoire des espèces peut être représentée par un arbre, dont les feuilles sont les espèces actuelles. Deux espèces sont considérées d’autant plus proches que leur espèce ancestrale commune est récente. Deux gènes de deux espèces différentes et issus d’un même gène ancestral sont dits « homologues ». Intuitivement, les séquences de deux gènes homologues se ressembleront d’autant plus que ce gène ancestral est récent. C’est cette similarité que les algorithmes de comparaison de séquences cherchent à mesurer.
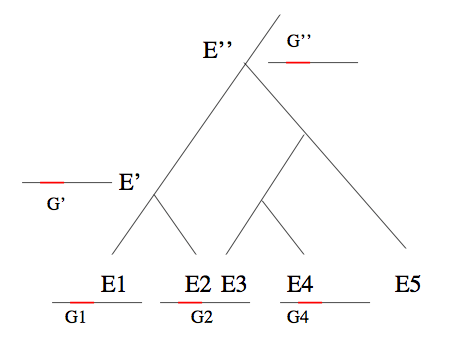
Arbre d’espèces, gènes homologues et similarité de séquences.
Les deux espèces E1 et E2 possèdent une espèce ancestrale commune (E’) plus récente que l’espèce ancestrale E’’ commune à E2 et E4. E1 et E2 seront donc considérées comme plus proches que E2 et E4. Les gènes G1 et G2, des génomes des espèces respectives E1 et E2, sont homologues car issus d’un gène ancestral commun G’ du génome de l’espèce E’. Il en est de même des gènes G2 et G4, dont le gène ancestral commun G’’ est cependant plus lointain. On peut donc s’attendre à ce que les séquences de G1 et G2 se ressemblent plus que celles de G2 et G4.
2. Comparaison et alignement
Il est facile de concevoir une mesure de similarité entre deux séquences de même longueur, par exemple en se limitant à compter le nombre de caractères qui diffèrent. Ainsi, sur la figure suivante, les deux séquences (b) seront considérées plus similaires que les deux séquences (a).

Exemple de la comparaison simple d’une paire de séquences sur toute leur longueur.
Compte tenu des critères retenus ici (nombre de caractères différents), les séquences de la paire (b) sont considérées comme plus similaires que celles de la paire (a).
Mais le problème de la comparaison de séquences est un peu plus compliqué, pour deux raisons. D’une part, les séquences à comparer ont rarement la même longueur ; et même quand c’est le cas, rien ne dit qu’elles doivent être comparées sur cette longueur exactement.

Alignement simple de deux séquences.
Les séquences en (a) sont peu similaires si comparées sur toute leur longueur (6 caractères différents) ; en (b), un simple décalage d’un caractère augmente la valeur de similarité (2 caractères différents seulement).
D’autre part, on vient de le voir, des nucléotides ou des acides aminés ont pu s’insérer ou au contraire disparaître au cours de l’évolution. Pour tenir compte de ces insertions ou délétions éventuelles, il faut introduire un caractère particulier, appelé gap et noté « — ». La mise en correspondance d’un caractère d’une séquence avec un gap dans l’autre séquence s’interprète soit comme une insertion du caractère dans la première séquence, soit comme une délétion d’un caractère dans la seconde, et rend compte d’une insertion ou d’une délétion d’un nucléotide dans la macromolécule d’ADN ou d’un acide aminé dans le polypeptide.
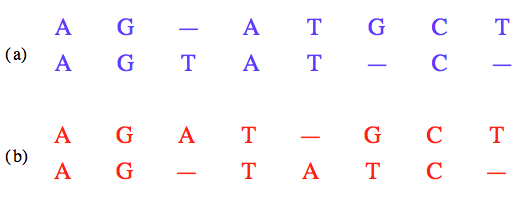
Deux alignements possibles de la même paire de séquences avec insertion de caractères gap.
Le calcul de la similarité de deux séquences requiert donc une opération préalable d’alignement, c’est-à-dire d’insertion de caractères gap dans l’une ou l’autre des séquences et de mise en correspondance des caractères de l’une avec les caractères de l’autre.
Pour chaque alignement, il est possible de calculer la similarité des deux séquences alignées, à condition bien entendu de s’être doté des critères nécessaires.
Il s’agit d’abord de se donner un tableau, dit « matrice de substitution », qui contient les coûts de la substitution d’un acide nucléique par un autre dans le cas de séquences génomiques, d’un acide aminé par un autre dans le cas de séquences polypeptidiques. Autrement dit, cette matrice fournit le coût de la mise en correspondance, dans un alignement, d’un caractère par un autre. Cette matrice est de taille 4 × 4 dans le cas de la comparaison de séquences génomiques et de taille 20 × 20 pour les séquences polypeptidiques.
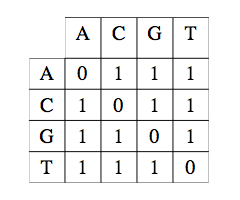
Matrice de substitution unité.
Ici, la mise en correspondance de deux caractères identiques est affectée d’un coût nul, la mise en correspondance d’un caractère avec un caractère différent est affectée du coût 1.
Les valeurs des éléments de la matrice de substitution traduisent évidemment des considérations biochimiques et évolutives.
À titre d’exemple, les bases distinguant les acides nucléiques se décomposent en deux groupes : les purines (Adénine et Guanine) et les pyrimides (Cytosine et Thymine). Les biologistes savent que la substitution d’un acide nucléique par un acide nucléique dont la base est du même groupe (appelée transition) est plus fréquente que les autres substitutions (appelées transversions). De ce fait, les substitutions de A par G et de G par A d’une part, de C par T et de T par C d’autre part, peuvent être moins pénalisées que les autres. Une matrice de substitution qui traduit cela est dite de « transition-transversion ».
De même, et toujours à titre d’exemple simple, la substitution d’un acide aminé hydrophobe par un autre hydrophobe sera moins pénalisée que sa substitution par un acide aminé hydrophile.
Il faut ensuite fixer un coût d’insertion ou de délétion, autrement dit le coût d’insertion d’un caractère gap.
Dans cette présentation, le coût d’insertion d’un gap est fixe. Or, il est possible de distinguer le coût dit d’ouverture d’une séquence de gaps du coût d’insertion d’un gap à la suite d’un ou plusieurs autres. Il est facile de modifier l’algorithme, afin de prendre en compte de telles fonctions de coût.
Un coût peut alors être calculé pour chaque alignement possible des deux séquences. Dans l’exemple donné ci-dessus, si la mise en correspondance de deux caractères identiques est affectée d’un coût nul, que la mise en correspondance d’un caractère avec un caractère différent est affectée du coût 1 (conformément à la matrice de substitution unité choisie ici), et que la mise en correspondance avec un gap est affectée du coût 2, alors l’alignement (a) a un coût de 6, et (b) de 7.
Parmi tous les alignements possibles, le principe est de retenir ceux (il peut y en avoir plusieurs) dont le coût est minimal. Un alignement de coût minimal est dit optimal. La similarité des deux séquences se mesure alors par ce coût minimal. Mais il est en pratique impossible d’énumérer tous les alignements possibles, car leur nombre est beaucoup trop élevé. La solution consiste à mettre en œuvre un algorithme qui calcule directement les alignements optimaux et le coût correspondant.
Au lieu d’affecter les mises en correspondance de caractères d’un coût et de chercher les alignements de coût minimal, il est tout aussi possible d’affecter un score d’autant plus grand que la correspondance est bonne et de chercher les alignements de score maximal. Le principe de l’algorithme, et en particulier le schéma de calcul, reste le même. Bien entendu, les valeurs des termes de la matrice de substitution et du coût d’insertion d’un gap sont déterminées en conséquence.
3. Principe d’un algorithme de recherche des alignements optimaux
La compréhension du principe de cet algorithme passe par une représentation graphique. On peut en effet visualiser les différents alignements possibles de deux séquences de longueur N et M comme autant de chemins menant du nœud (0, 0) au nœud (N, M) d’une grille où chaque colonne correspond à une lettre de la première séquence et chaque ligne à une lettre de la seconde.
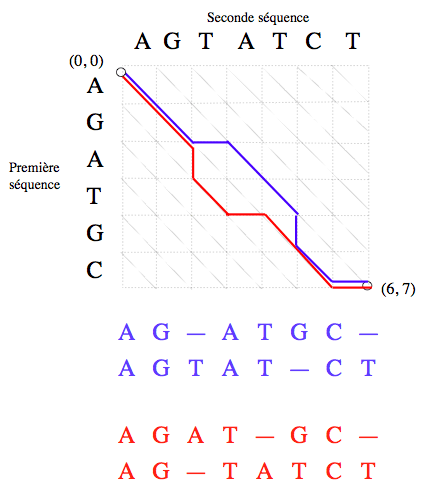
Représentation graphique des alignements.
Un alignement des séquences « AGATGC » et « AGTATCT » est un chemin menant du nœud (0, 0) au nœud (6, 7) (les nœuds se situent à l’intersection des lignes en pointillés). Ici sont représentés, en bleu et en rouge, deux exemples d’alignement.
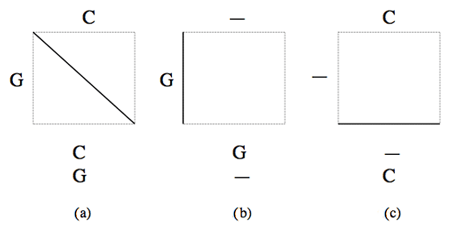
Dans chaque case de la grille, un trait en diagonale (a) indique la mise en correspondance d’un caractère d’une séquence avec un caractère de l’autre, un trait vertical (b) indique la mise en correspondance d’un caractère de la première séquence avec un gap inséré dans la seconde, et un trait horizontal (c) l’insertion d’un gap dans la première séquence en face d’un caractère de la seconde.
Animation : expérimenter le tracé d’un chemin
Nous vous proposons, à l’aide d’une animation HTML5/JS, d’expérimenter le tracé d’un chemin, dans le cas où les coûts de mise en correspondance d’un caractère avec un caractère différent d’une part et de mise en correspondance avec un gap d’autre part valent 1.
Animation : chercher un chemin optimal
L’algorithme a pour but de déterminer, parmi tous les chemins possibles, ceux dont le coût est minimal. À l’aide de l’animation, nous vous proposons à présent de chercher un chemin optimal.
Le principe de l’algorithme repose sur une remarque simple. Imaginons qu’il ait été trouvé un chemin optimal du nœud (0, 0) au nœud (N, M), de longueur L, c’est-à-dire composé de L segments verticaux, horizontaux ou obliques. Le sous-chemin de longueur L-1, composé des L-1 premiers segments du chemin complet, correspond à l’alignement complet privé de la dernière paire de caractères mis en correspondance. Puisque le chemin complet est optimal, ce sous-chemin l’est aussi. En effet, si ce n’était pas le cas, cela signifierait qu’il existe un autre sous-chemin de longueur L-1 arrivant sur le même avant-dernier nœud du chemin complet, mais d’un coût inférieur ; le chemin complet qui incorporerait ce sous-chemin posséderait de ce fait un coût inférieur au chemin complet optimal, ce qui est contradictoire.
Le même raisonnement permet d’affirmer que le sous-chemin de longueur L-2, et l’alignement partiel associé, est également optimal. Par récurrence, tous les sous-chemins d’un chemin optimal sont optimaux ; autrement dit, tous les alignements progressifs partiels qui composent un alignement optimal sont optimaux.
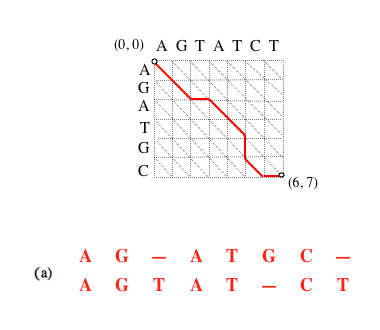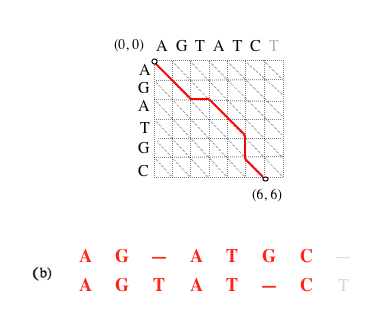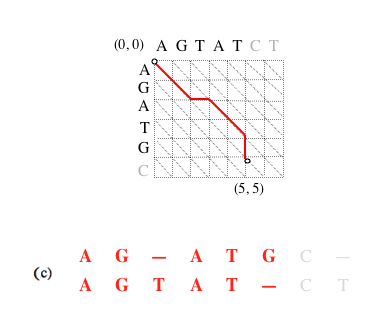
Si le chemin complet (a) est optimal, alors le sous-chemin (b) obtenu en supprimant le dernier segment l’est aussi, et ainsi de suite (c).
Supprimer le dernier segment revient à considérer l’alignement amputé de la dernière paire de caractères mis en correspondance. L’alignement (a) est l’alignement optimal des séquences AGATGC et AGTATCT (matrice de substitution unité et coût d’insertion de gap égal à 1) ; le (b) des séquences AGATGC et AGTATC ; le (c) des séquences AGATG et AGTAT.
Ce résultat permet de concevoir une démarche de construction d’un alignement optimal de deux séquences de longueurs N et M. Un alignement (ou chemin) optimal de longueur L s’obtient, on vient de le voir, en complétant un alignement partiel (ou sous-chemin) optimal de longueur L-1. Or, il n’existe que trois sous-chemins de longueur L-1 du chemin arrivant au nœud (N, M) : celui qui arrive au nœud (N, M-1), celui qui arrive au nœud (N-1, M-1) et celui qui arrive au nœud (N-1, M). Supposons que les coûts des chemins optimaux arrivant sur ces nœuds soient connus ; appelons-les C N, M-1, C N-1, M-1 et C N-1, M. Le chemin optimal arrivant sur le nœud (N, M) se détermine alors facilement : il suffit de tracer le segment à partir du nœud, parmi les trois possibles, qui correspond à la plus petite des trois valeurs C N, M-1 + β, C N-1, M-1 + α N, M et C N-1, M + β, où β est le coût d’insertion d’un gap et α N, M est le coût de mise en correspondance du caractère de rang N dans la première séquence et du caractère de rang M dans la seconde ; cette valeur α N, M est fournie par la matrice de substitution. Il est facile de voir que n’importe quel autre choix conduirait à un alignement plus coûteux, et donc non-optimal.
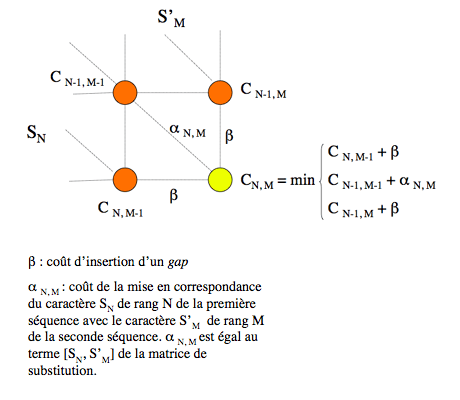
Il n’y a que trois nœuds (en orange) par lesquels peut passer un chemin arrivant sur le nœud (N, M) (en jaune).
Si les coûts des chemins optimaux qui y arrivent sont connus, il est simple de déterminer le dernier segment à tracer pour que le chemin complet arrivant sur le nœud (N, M) soit optimal : c’est celui pour lequel la somme du coût qui lui est associé et du coût de la mise en correspondance des deux caractères des séquences en ligne et en colonne est la plus petite des trois.
Fort bien, mais nous avons supposé que les coûts des alignements optimaux arrivant sur les nœuds (N, M-1), (N-1, M-1) et (N-1, M) étaient connus. Comment les obtenir ? La solution est immédiate : il suffit d’appliquer la même démarche à chacun de ces trois nœuds, et ainsi de suite jusqu’à retrouver le nœud origine (0, 0). Ainsi, le problème de calculer un alignement optimal se ramène à calculer trois alignements optimaux plus courts ; chacun d’entre eux demande à son tour le calcul de trois alignements optimaux encore plus courts, et ainsi de suite. Ce calcul, dit « récursif », s’arrête sur le nœud origine (0, 0). Il est possible de programmer directement ce schéma sous la forme d’une procédure récursive qui calcule le coût optimal en un nœud (i, j) en effectuant trois appels à elle-même pour calculer les coûts minimaux des trois chemins arrivant au nœud (i, j-1), au nœud (i-1, j-1) et au nœud (i, j-1). Cette procédure est initialement activée sur le nœud (N, M).
Cette mise en œuvre récursive se révèle cependant extrêmement peu efficace, car un même alignement partiel doit être calculé plusieurs fois.
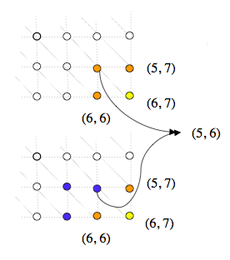
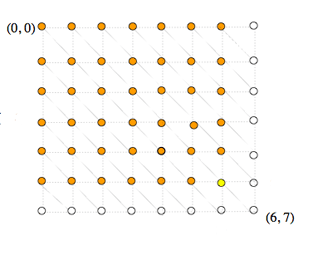
Lors de la démarche récursive de détermination du coût du chemin optimal arrivant sur un nœud, le coût d’un même sous-chemin est calculé plusieurs fois, pénalisant lourdement l’efficacité de l’algorithme.
Sur cet exemple, à gauche, on voit que le calcul du coût au nœud (6, 7) en jaune requiert le calcul des coûts aux nœuds (6, 6), (5, 6) et (5, 7) en orange. Le calcul du coût au nœud (6, 6) requiert à son tour le calcul des coûts aux nœuds en bleu (6, 5), (5, 5) et de nouveau (5, 6). Or, le calcul du coût au nœud (5, 6) est évidemment lui-même récursif et entraîne, à chaque fois qu’il est lancé, le calcul des coûts de tous les nœuds (i, j) où i ≤ 5 et j ≤ 6 (en orange à droite). Ces nœuds sont eux-mêmes calculés suivant le même schéma, et ainsi de suite. Si bien que le nœud (1, 1) par exemple sera calculé plusieurs dizaines de fois.
À cette démarche récursive est donc préférée une mise en œuvre itérative, nettement moins gourmande en temps et en espace mémoire, qui aboutit à l’algorithme d’alignement optimal de Needleman et Wunsch, présenté à la section suivante.
Une procédure récursive est une procédure qui, lors de son exécution, fait un ou plusieurs appels à elle-même. Il est assez fréquent de rencontrer des problèmes dont la formulation semble conduire naturellement et élégamment à l’écriture d’une procédure récursive pour l’obtention de leurs solutions. Une analyse plus attentive peut en fait montrer l’existence d’une méthode de résolution itérative. C’est le cas de la recherche des alignements optimaux de deux séquences telle qu’exposée ici. La méthode itérative est généralement préférée, car plus économe en temps comme en place mémoire. Il existe cependant des algorithmes qui ne peuvent pas se programmer autrement que sous une forme récursive.
Cet algorithme, présenté ici sur des exemples de séquences de nucléotides, s’applique également sur des séquences d’acides aminés. En fait, il a initialement été conçu pour comparer de telles séquences (Needleman et Wunsch, 1970, « A general method applicable to the search of similarities in the amino acid sequence of two proteins », J. Mol. Biol. 48: 443-453). Dans l’évaluation des coûts, une matrice 20 x 20 donne les différents coûts de substitution d’un acide aminé par un autre.
4. L’algorithme d’alignement optimal
L’algorithme se déroule en deux grandes étapes. La première consiste à calculer itérativement les (N+1) × (M+1) coûts des chemins optimaux qui partent du nœud (0, 0) et arrivent sur un nœud (i, j), avec 0 ≤ i ≤ N et 0 ≤ j ≤ M et qui correspondent aux alignements optimaux des i premiers caractères de la première séquence avec les j premiers de la seconde.
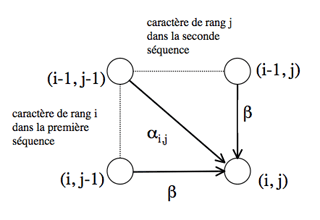
Le chemin aboutissant au nœud (i, j) passe obligatoirement par l’un des trois nœuds (i-1, j-1), (i-1, j) ou (i, j-1).
Les chemins aboutissant à ces nœuds sont optimaux par construction. Pour que le chemin aboutissant au nœud (i, j) le soit, il faut et il suffit que la somme du coût attaché au nœud qui le précède et du coût de passage de ce nœud au nœud (i, j) soit minimale.
Il est possible de déterminer le coût minimal du chemin qui aboutit sur le nœud (i, j) si les coûts C i-1, j-1, C i, j-1 et C i-1, j des chemins optimaux arrivant respectivement sur les nœuds (i-1, j–1), (i, j-1) et (i-1, j) ont été calculés lors des itérations précédentes : c’est la plus petite des trois valeurs C i-1, j-1 + α i, j, C i, j-1 + β, C i-1, j + β, où α i, j est le coût de mise en correspondance du caractère situé à la position i dans la première séquence avec le caractère situé en position j de la seconde (α i, j est égal au terme [Si, S’j] de la matrice de substitution, où Si est le caractère de rang i de la première séquence, et S’j le caractère de rang j de la seconde), et β est le coût d’insertion d’un gap dans l’une ou l’autre séquence.
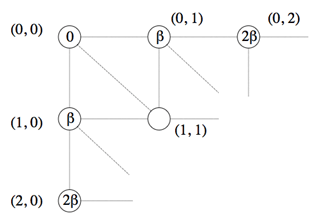
Début du calcul itératif.
En partant du nœud (0, 0), il n’y a qu’une seule façon de passer au nœud (0, 1), et donc un seul chemin, qui de ce fait est optimal : en traçant un segment horizontal, ce qui correspond à l’insertion d’un caractère gap dans la première séquence, de coût β. De même, il n’existe qu’une seule possibilité pour passer au nœud (1, 0) : insérer un caractère gap dans la seconde séquence, de coût β également. Il est alors possible de calculer le coût minimal du chemin menant au nœud (1, 1).
Cette fois, le calcul part du nœud (0, 0). Le coût de l’alignement optimal aboutissant au nœud (0, 1) se calcule à partir du coût nul associé au nœud (0, 0) : la seule possibilité pour passer de l’un à l’autre est de faire correspondre un gap au premier caractère de la seconde séquence, opération de coût β. Le nœud (0, 1) se voit donc associer le coût 0 + β, soit β. Il en va de façon symétrique pour le nœud (1, 0) qui se voit également associer le coût β. Les coûts des nœuds (2, 0), (1, 1) et (0, 2) peuvent alors être calculés.
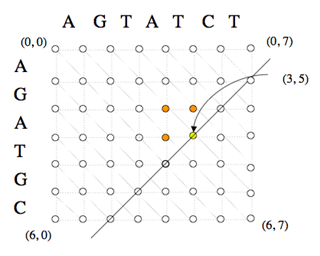
Le calcul des coûts des chemins optimaux partant du nœud (0, 0) et aboutissant à chaque nœud (i, j) s’effectue de façon itérative, à partir du coût nul associé au nœud (0, 0).
Par exemple, le coût associé au nœud (3, 5), en jaune, peut être calculé à partir des coûts associés aux nœuds (2, 5), (3, 4) et (2, 4), en orange, calculés antérieurement. Les nœuds d’une même diagonale peuvent être calculés dans un ordre quelconque, ce qui a permis d’implémenter des versions parallèles de cet algorithme.
Il est ainsi facile de déterminer de proche en proche le coût de l’alignement optimal partiel qui se termine en chaque nœud (i, j), et donc de l’alignement complet au nœud (N, M). Compte-tenu du schéma expliqué ci-dessus, tous les coûts d’une même diagonale peuvent être calculés à partir des valeurs portées par la diagonale précédente.
Animation : visualiser la phase 1 de l’algorithme
Le résultat de cette première phase de l’algorithme est donc un tableau à N+1 lignes et M+1 colonnes qui contient, pour chaque nœud (i, j), la valeur du coût du chemin optimal du nœud (0, 0) à ce nœud (i, j), autrement dit le coût du meilleur alignement impliquant les i premiers caractères de la première séquence et les j premiers de la seconde. C’est bien entendu la valeur au nœud (N, M) qui est importante, puisque c’est celle qui est associée à l’alignement optimal des séquences complètes. Mais ce tableau ne dit pas quel est cet alignement.
Pour connaître l’alignement optimal, il faut, dans la seconde phase de l’algorithme, repartir de ce nœud (N, M) et cheminer « en arrière » en choisissant à chaque fois la direction qui ramène au nœud, parmi les trois possibles, auquel est associée, suivant le même principe que précédemment, la plus petite des trois valeurs C i-1, j-1 + α i, j, C i, j-1 + β, C i-1, j + β (qui est de fait égale à C i, j) et ainsi de suite jusqu’au nœud (0, 0). Le chemin ainsi tracé fournit l’alignement.
Animation : retrouver les alignements optimaux
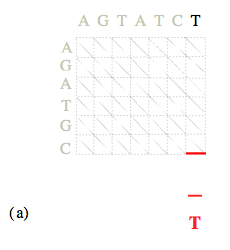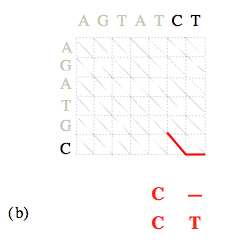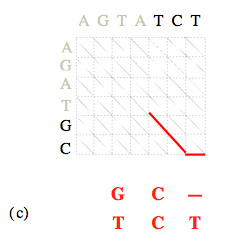
Une fois la matrice des coûts calculée, la détermination des alignements optimaux se fait en « remontant » du nœud (N, M) au nœud (0, 0).
Les coûts de chemins optimaux arrivant sur chacun des (N 1)×(M 1) nœuds ayant été calculés lors de l’étape précédente, il suffit à chaque nœud (i, j) de retenir, parmi les trois nœuds « amont » possibles, celui associé à la plus petite des trois valeurs C i-1, j-1 + α i, j, C i, j-1 + β, C i-1, j + β. L’alignement se construit ainsi progressivement « de la droite vers la gauche ».
Il faut noter que le nombre d’opérations de ce cheminement « en arrière » est bien inférieur au nombre d’opérations effectuées lors de la première étape, puisque l’opération qui consiste à retenir le minimum des trois sommes ne doit être effectuée ici que L fois, où L est du même ordre que les longueurs N ou M (L est au plus égal à N + M), et non plus de l’ordre de N × M. Par ailleurs, il se peut qu’à partir d’un nœud donné, plus d’un nœud puisse être retenu ; cela signifie qu’il existe plusieurs alignements optimaux qu’il est possible de générer.
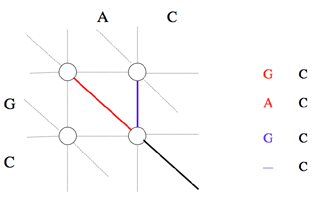
Dans la seconde phase de l’algorithme, il se peut qu’à une certaine étape de la remontée du nœud (N, M) au nœud (0, 0) plus d’un nœud puisse être retenu.
C’est le cas si deux des trois sommes C i-1, j-1 + α i, j, C i, j-1 + β, C i-1, j + β sont égales, et inférieures à la troisième ; ou encore lorsque les trois sommes sont égales. Cela signifie qu’il existe plusieurs alignements différents, mais tous optimaux (et donc de même coût). Il faut alors poursuivre chacun des chemins, afin de produire ces différents alignements.
Animation : visualiser la phase 2 de l’algorithme
Programmation dynamique et principe de Bellman – Pontryagin
Cet algorithme de recherche des alignements optimaux de deux séquences appartient à la classe des algorithmes dits de « programmation dynamique ». Ces algorithmes mettent en œuvre un schéma de résolution qui détermine une solution optimale d’un problème à partir des solutions de tous les sous-problèmes. Les problèmes ainsi traités satisfont le principe de Bellman – Pontryagin, qui se traduit, sur le cas de l’alignement de séquences, par la propriété d’un alignement optimal d’être composé d’alignements partiels optimaux.
Précisons que dans l’expression « programmation dynamique », le terme « programmation » ne se réfère pas à la notion de programme d’ordinateur, mais plutôt de planification.
Animation : choisissez d’autres séquences…
Vous pouvez maintenant relancer le programme en choisissant vous-mêmes les deux séquences à aligner, la matrice de substitution, et le coût d’insertion d’un caractère gap. Pour un meilleur affichage, choisissez des séquences assez courtes.
Les séquences d’acides nucléiques sont formées à partir des quatre lettres A, C, G, T. Pour ces séquences, vous avez le choix entre la matrice unité et une matrice qui tient compte du fait que les mutations de A en G et de G en A d’une part, de C en T et de T en C d’autre part, sont plus fréquentes que les autres. Cette matrice est dite de « transition-transversion ». Vous pouvez faire apparaître les valeurs de la matrice en cliquant sur l’icône associée. Notez que ce sont les valeurs relatives des éléments de la matrice qui sont déterminantes, mais que la valeur du coût d’insertion d’un gap doit être choisie en conséquence.
Vous pouvez également faire fonctionner l’algorithme sur des séquences polypeptidiques, formées à partir des 20 lettres initiales des acides aminés. Dans ce cas, la seule matrice de substitution qui vous est accessible est la matrice dite PAM250, que vous devez afficher si vous voulez comprendre les coûts de substitution utilisés par l’algorithme lors du calcul des coûts d’alignement (phase 1).
L’animation HTLM5/JS a été adaptée d’une applet réalisée par Régis Monte, adaptation par Centrale Lille Projets modifiée et finalisée par Ouest INSA.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !
