Vers l’ordinateur quantique : un défi scientifique majeur pour les prochaines décennies

NDLR : Cet article reflète l’état de l’art sur la question il y a 15 ans.

1. Physique quantique et information : perspectives audacieuses pour l’informatique

Dès 1982, Richard Feynmann, Prix Nobel de Physique, suggérait que d’utiliser la physique quantique au lieu de la physique classique comme support matériel de l’information et du calcul permettrait de traiter des problèmes que leur complexité met hors de portée de l’informatique actuelle. C’est au cours des années quatre-vingt-dix que des premiers résultats, d’abord algorithmiques et théoriques, puis expérimentaux, sont venus confirmer de manière éclatante cette intuition initiale.

De la théorie à l’expérimentation

En 1994, Peter Shor (AT&T) montre en effet que le calcul quantique permet de factoriser les entiers en temps polynomial, alors que le meilleur algorithme classique connu a un coût exponentiel. En 1996, Lov Grover (Lucent) conçoit un algorithme quantique qui n’a besoin que de √n requêtes à un oracle f pour trouver un élément qui satisfait f dans une base de données non ordonnée de taille n, là où le calcul classique requiert de l’ordre de n requêtes au même oracle. Quelques conséquences de ces deux résultats majeurs sont expliquées plus loin (voir partie 4).

Un peu plus tôt, en 1993, Charles Bennett (IBM Research), Gilles Brassard (université de Montréal) et quelques autres mettaient en évidence un usage inattendu de l’intrication, propriété de l’information quantique tellement étrangère au monde classique que des personnages comme Einstein en avaient, dès 1935, vigoureusement contesté la réalité. Le travail de Bennett et de ses collègues définissait les principes théoriques d’un protocole de « téléportation » : l’état d’un système quantique a (une particule, par exemple) localisé en A peut, après avoir été détruit, être attribué à un autre système quantique b localisé ailleurs, en B, sans que l’état de a ne soit connu ni en A ni en B, et sans que ni a ni aucun autre système quantique porteur de l’état de a ne soit transporté sur une trajectoire reliant A et B. Peu après, en 1997, Anton Zeilinger (université de Vienne) réalise selon ces principes la première expérience de téléportation de l’état d’un photon, suivie depuis de beaucoup d’autres, avec d’autres particules.

Isaac Chuang devant son ordinateur quantique chez IBM.
Photo © IBM.

De 1999 à 2002, Isaac Chuang (IBM Research) conçoit et réalise un ordinateur quantique qui, bien que limité à 7 bits, lui sert à montrer que la physique permet en effet de mettre en œuvre expérimentalement les principes algorithmiques nouveaux imaginés sur le plan théorique par Peter Shor et Lov Grover.

Un foisonnement interdisciplinaire

Ces splendides résultats théoriques sur l’information quantique et son traitement, puis leurs confirmations expérimentales, ont immédiatement suggéré que des problèmes hors de portée de l’informatique classique pourraient être traités en exploitant ce paradigme informationnel radicalement non classique. Ils ont ouvert des perspectives scientifiques et technologiques lointaines, certes, mais immenses. Ces travaux ont donné naissance à un courant de recherche interdisciplinaire, aujourd’hui très foisonnant où physiciens, théoriciens et expérimentalistes, mathématiciens et informaticiens apportent désormais des contributions majeures. Des liens profonds ont été établis entre les disciplines jusqu’alors disjointes de la physique quantique, de l’informatique et de la théorie de l’information. La douzaine de pionniers de la fin des années quatre-vingts est devenue une communauté de plusieurs milliers de personnes qui a ses groupes de recherche renommés, ses conférences internationales, ses écoles d’été et ses journaux scientifiques, où se rencontrent, s’expriment et coopèrent des chercheurs de toutes ces disciplines.

Cette recherche vise le très long terme. Il n’y aura probablement pas d’ordinateur quantique de taille utile avant plusieurs dizaines d’années. Cette recherche a devant elle de grandes questions, souvent difficiles, et même quelques obstacles qui semblent encore insurmontables aujourd’hui. Mais elle a la dynamique, l’imagination et l’audace de la jeunesse. C’est en effet un grand défi scientifique que de porter ce regard neuf sur la connaissance ultime que nous avons, aujourd’hui, de la matière, au niveau le plus profond de sa constitution, pour y distinguer ce qui peut s’interpréter comme de l’information, et pour y trouver ce que nous serons peut-être un jour en mesure de maîtriser pour traiter et communiquer cette information, à des échelles et avec des performances aujourd’hui inconcevables, et pour des applications encore impossibles à imaginer.

2. Retour sur les fondements physiques de l’informatique

L’informatique actuelle code l’information avec des bits qui sont soit dans l’état 0, soit dans l’état 1. Ces bits sont organisés en registres, et l’état d’un registre, qui code une valeur utilisée lors d’un calcul, n’est autre que la suite des états des bits qui composent ce registre. Au cours d’un calcul, l’état des registres pourra être transformé, pourra être recopié dans d’autres registres, puis l’état de l’un de ces registres sera lu à la fin pour produire un résultat. En général, les transformations d’états effectuées pendant le calcul ne sont pas réversibles, c’est-à-dire qu’il n’y a plus assez d’information dans l’état d’après pour reconstituer l’état d’avant. D’autre part, l’état des registres ne sera en rien perturbé par la lecture de leur contenu, et la lecture de deux registres qui sont dans le même état donnera toujours un résultat identique. Cet énoncé simpliste de ce qui se passe au cours d’un calcul n’en dit évidemment presque rien, mais il suffit pour amener une question fondamentale, et rarement posée dans les milieux informaticiens : sur quoi l’informatique actuelle se fonde-t-elle pour fonctionner ainsi ?

Prenons un peu de recul. Quelles que soient les lois de la nature que l’on choisit d’exploiter pour concevoir le fonctionnement d’une machine à traiter l’information, l’information est incarnée dans la matière sous la forme d’états de cette matière, et le traitement de cette information est incarné dans des processus qui, avec un apport d’énergie, agissent sur cette matière pour transformer son état. Il ne peut pas y avoir d’information sans support physique, pas de calcul sans processus physique, si bien que les lois de la physique sont en amont de celles du calcul, qu’elles gouvernent toute forme possible de calcul. Sachant cela, la réponse à la question posée plus haut est brève, à défaut d’être évidente : si l’informatique actuelle peut fonctionner comme elle fonctionne, c’est qu’elle est fondée sur les lois de la physique classique, celle de Newton et de Maxwell. Et, aussi surprenant que cela paraisse, cette affirmation qui ramène tout à la physique vaut autant pour les ordinateurs du commerce que pour leurs modèles théoriques les plus abstraits, comme la machine de Turing ou le lambda-calcul.

Pascaline		Pentium 4.
Des premières machines à calculer aux microprocesseurs les plus récents, le support de l’information obéit aux lois de la physique classique. (Photos : André Devaux)

Pour nous en convaincre, empruntons un chemin détourné. Déracinons l’informatique du terrain de la physique classique pour la replanter dans celui de la physique quantique, celle qui a mis en évidence les propriétés des particules élémentaires. On se limitera ici à contempler, sans les expliquer en détail, les conséquences radicales de cette transplantation sur les quelques rudiments d’informatique évoqués précédemment.

3. Les étrangetés de l’information quantique

Une des expériences les plus simples qui met en évidence un phénomène quantique : interférences lumineuses à travers les fentes de Young. L’interprétation classique de cette expérience parle d’interférences entre ondes lumineuses. Or les mêmes franges d’interférences sont observées si on envoie des photons un par un dans les fentes de Young. Seule la mécanique quantique peut rendre compte de cette situation.

Les bits seront donc désormais des bits quantiques, des qubits : ils pourront être soit dans l’état 0, soit dans l’état 1, mais aussi, privilège du monde quantique, dans une superposition des deux, 0 et 1 à la fois. L’état d’un registre de 2 qubits pourra alors être 0, 1, 2 ou 3, mais aussi une superposition d’une partie quelconque de ces quatre états de base, voire même les quatre à la fois. L’état d’un registre de n qubits pourra être une superposition d’un ensemble quelconque des 2ⁿ valeurs possibles sur n bits, y compris une superposition de toutes ces valeurs à la fois, alors qu’un registre de n bits classiques ne peut contenir, à chaque instant, qu’une seule de ces valeurs. Conséquence : comme les calculs transformeront l’état de tels registres, toute opération effectuée lors d’un calcul quantique pourra agir simultanément sur 2ⁿ valeurs différentes. Ceci apporte un parallélisme massif : si une fonction peut être calculée avec 2ⁿ arguments différents, on calculera toutes ses valeurs simultanément. Les lois de la physique quantique imposent que ces calculs simultanés soient déterministes et réversibles, ce qui ne restreint en rien ce qu’on peut calculer, mais elles interdisent aussi de recopier l’état d’un registre dans un autre registre. Conséquence : dans un programme, on ne pourra pas affecter la valeur d’une variable quantique à une autre, ni utiliser cette valeur plus d’une fois. Ceci conduit à inventer une algorithmique radicalement nouvelle, et des langages de programmation qui respectent ces lois du monde quantique.

Une fois un calcul terminé, le résultat recherché est l’une des valeurs superposées dans un registre. Comment extraire ce résultat ? En effectuant ce que les physiciens appellent une mesure de ce registre : selon les lois de la physique quantique, la mesure pourra produire l’une quelconque des valeurs superposées dans le registre, chacune avec une certaine probabilité et, en même temps, elle réduira la superposition que contenait le registre à une seule valeur, celle qui aura été choisie. La mesure provoque donc l’effondrement des états superposés, et si deux registres contenaient la même superposition, rien ne garantit que leur mesure produira un résultat identique. Mais finit-on quand-même par obtenir ainsi le résultat que l’on cherche ? Oui, si l’algorithme (quantique) a été bien conçu. Conséquence : tout le jeu de l’algorithmique quantique a pour but d’amener aussi près de 1 que possible la probabilité d’obtenir un résultat pertinent, et cela en effectuant aussi peu d’opérations que possible.

Prenons enfin deux objets, A et B, qui ont chacun plusieurs états possibles. Alors que la physique classique, et notre expérience quotidienne, nous disent que l’état du couple (A,B) qu’ils constituent n’est autre que le couple (état de A, état de B), ceci n’est plus vrai dans le monde quantique. Dans cet autre monde, il se peut en effet que seul le couple (A,B) possède un état, alors que ni A ni B n’en ont un qui leur soit propre. On dit alors que A et B sont intriqués. Sans équivalent dans le monde classique, l’intrication est une ressource extraordinaire. Exemple : si A et B sont des registres de qubits, et s’ils ont été intriqués lors d’un calcul, on peut imaginer l’état du couple (A,B) comme reliant indissociablement chacune des valeurs superposées dans A à une ou plusieurs des valeurs superposées dans B. Conséquence : si on mesure A, son état se réduit à une seule des valeurs qu’il contenait, mais l’état de B se réduit aussi, au même instant, à la superposition des valeurs qui étaient reliées à celle qui est restée dans A. Ceci est vrai si A et B sont côte à côte, mais demeure vrai s’ils ont été éloignés de millions de kilomètres l’un de l’autre après avoir été intriqués : le couple (A,B) est toujours le couple (A,B), quelle que soit la distance qui sépare ses constituants. C’est cette non localité de la physique quantique qui avait tant choqué, en 1935, l’inventeur de la relativité. Il a fallu plusieurs décennies pour comprendre que cette « action fantomatique à distance », comme Albert Einstein l’avait appelée, ne transporte pas d’information. On sait aujourd’hui que l’intrication, associée à de la communication classique, rend possible la téléportation des états quantiques.

4. Deux grands résultats et leurs conséquences

C’est dans la première moitié des années quatre-vingt-dix que deux résultats théoriques majeurs ont donné le véritable signal de départ aux recherches aujourd’hui foisonnantes sur l’information quantique et son traitement : l’algorithme quantique de Shor (1994) pour la factorisation des entiers, et l’algorithme quantique de Grover (1996) pour la recherche d’un élément dans une base de données non ordonnée.

Que changerait l’algorithme de Shor ?

Prenons un exemple de problème qui peut devenir insurmontable pour l’informatique classique : la factorisation des entiers. Considérons un nombre entier, très grand, dont on sait qu’il est le produit de deux nombres premiers, mais on ne sait pas lesquels. Le problème de la factorisation est de trouver ces deux nombres. C’est un problème simple à poser, mais il excite les mathématiciens depuis plus de deux millénaires. En effet, s’il faut n chiffres pour écrire notre nombre, on ne connaît encore aucune méthode, ni à la main ni avec les ordinateurs actuels, qui garantisse qu’on puisse trouver ces deux facteurs en effectuant un nombre d’opérations qui ne soit pas une fonction exponentielle de n : tous les algorithmes classiques connus pour la factorisation sont de complexité exponentielle. Pour chacun de ces algorithmes, on connaît une formule qui, étant donnée la valeur de n, permet de déterminer l’ordre de grandeur du nombre d’opérations qu’il devra effectuer. Par exemple, le meilleur de ces algorithmes devra effectuer de l’ordre de 10²⁶ opérations (1 suivi de 26 zéros) pour factoriser un nombre de 300 chiffres. Imaginons alors que nous ayons à notre disposition l’ordinateur le plus puissant qu’on sache construire aujourd’hui, dont les performances sont de l’ordre de 100 teraflops (10¹⁴ opérations par seconde). Pour trouver les deux facteurs de notre nombre de 300 chiffres, c’est-à-dire pour effectuer 10²⁶ opérations à raison de 10¹⁴ opérations par seconde, il lui faudra 10¹² secondes, c’est-à-dire 30 000 ans ! Paradoxalement, l’obstacle que constitue cette complexité présente un grand intérêt, car c’est précisément sur la difficulté à le franchir que repose la sécurité des systèmes de cryptage les plus répandus, comme ceux qui sont utilisés sur Internet pour transmettre des informations confidentielles.

Ce que Peter Shor a montré est que, si on remplace nos vieux principes de calcul par ceux de l’informatique quantique, on pourra alors trouver les deux facteurs premiers de notre nombre de n chiffres en n³ opérations élémentaires, soit de l’ordre de 10⁷ opérations pour un nombre de 300 chiffres. Si l’ordinateur, maintenant quantique, effectue une opération par microseconde, ce qui est modeste, il lui suffira de 10 secondes pour trouver les deux facteurs. C’est ce résultat de Shor, en 1994, qui a mis le feu aux poudres pour les recherches sur le calcul quantique : à toute une classe de problèmes, dont fait partie la factorisation, le calcul quantique apportera des chutes exponentielles de complexité par rapport à ce qu’on sait faire de mieux pour ces problèmes avec le calcul classique. Les conséquences concrètes n’en sont peut-être pas très nombreuses, mais elles sont de taille : si, un jour encore lointain, un ordinateur quantique arrive sur le marché, il suffira de quelques minutes pour faire voler en éclats tous les systèmes de cryptage actuels.

L’information quantique détruira donc d’une main la cryptographie classique, qui est fondée sur des obstacles algorithmiques auxquels on accorde encore une certaine confiance, bien que leur robustesse ne soit pas prouvée. Mais elle reconstruit déjà de l’autre main une cryptographie quantique bien différente, évoquée plus loin (voir partie 6), dont la sûreté est beaucoup plus définitive, car fondée sur des propriétés physiques de la matière à l’échelle quantique.

Qu’apporte l’algorithme de Grover ?

Le problème traité par Grover est bien différent. Un exemple simple suffit pour apprécier la portée de son résultat. Considérons un annuaire téléphonique qui contient les noms et numéros de 10⁶ abonnés, rangés dans l’ordre alphabétique de leurs noms, si bien qu’aucun ordre ne préside au rangement des numéros les uns par rapport aux autres. Si cet annuaire est la seule base de données dont on dispose sur le numéro affecté à chaque abonné, la recherche du nom de l’abonné ayant un numéro donné exigera, à la main ou avec un ordinateur actuel, de l’ordre de 10 ⁶ comparaisons entre ce numéro et ceux que contient l’annuaire (5.10⁵ en moyenne pour trouver la bonne réponse).

Ce que Grover a montré, c’est que les principes du calcul quantique permettront de trouver la réponse en faisant un nombre de comparaisons égal à la racine carrée de la taille de la base de données, c’est-à-dire, dans le cas de notre annuaire, mille comparaisons. Les principes mêmes de l’informatique classique lui interdisent l’accès à une telle chute quadratique de complexité pour ce problème simple. Cette chute est moins impressionnante que l’accélération exponentielle dont bénéficie la classe des problèmes traités par Shor, mais elle concerne la recherche d’information, c’est-à-dire une famille de problèmes omniprésents et d’importance cruciale en traitement de l’information.

5. Alors, l’ordinateur quantique, c’est pour quand ?

Cette question est encore sans réponse. La communauté internationale des chercheurs sur le traitement et la communication de l’information quantique est actuellement composée de 85% de physiciens, théoriciens et expérimentalistes, et de 15% d’informaticiens, ces derniers plutôt sur le versant mathématique et logique de leur discipline. Du côté de la physique, le problème est facile à poser : comment inscrire le bit quantique dans la matière ? Mais c’est un problème redoutablement difficile, car la Nature lui oppose un grand obstacle que les physiciens appellent « décohérence ».

Tout algorithme quantique qui utilise un registre A de n qubits suppose que l’état de ce registre est une superposition de tout ou partie des 2ⁿ états de base possibles, et que si l’état du registre A est intriqué avec l’état du registre B, ceci est une conséquence voulue du calcul en cours. Or, les particules qui peuvent servir à réaliser physiquement des qubits (électrons, ions, photons…) ont la fâcheuse propriété d’entrer naturellement dans des états intriqués avec les particules qui, nécessairement, composent la matière dans leur proche voisinage : c’est le processus, inévitable, de la décohérence. Quand ce processus a fait son effet, ce qui prend un certain temps, en général minuscule, l’état de notre registre ne reflète plus fidèlement ce qui était voulu par le calcul, car il participe à ces états intriqués indésirables : l’état du registre n’est plus « cohérent ». Pire encore, plus notre registre comporte de qubits, plus le temps pendant lequel il reste cohérent, donc pertinent pour le calcul, devient court.

Franchir cet obstacle est crucial si l’on veut réaliser un ordinateur quantique. Cela exige la solution de deux sous-problèmes. Le premier est de nature mathématique et logique : il faut des codes quantiques correcteurs d’erreurs. Plusieurs solutions ont déjà été élaborées, mais ces solutions ont elles-mêmes un coût : coder ainsi un qubit logique coûte de 5 à 9 qubits physiques, selon la solution choisie, ce qui empire évidemment la situation, et la récupération d’erreur coûte du temps, ce temps justement si précieux contre lequel il faut courir pour échapper à la décohérence. Le deuxième sous-problème est de nature physique. Il est maintenant admis qu’une réalisation physique du qubit ne sera viable que si elle garantit un temps avant décohérence de l’ordre de 10⁴ fois le temps nécessaire à l’exécution d’une opération élémentaire sur un qubit. Ceci est nécessaire pour appliquer les procédures de correction d’erreurs après chaque opération. C’est un critère difficile à satisfaire, mais ce n’est pas le seul.

Il faut aussi, évidemment, que la mise en œuvre physique permette d’effectuer des calculs, c’est-à-dire d’appliquer des opérateurs quantiques aux qubits et aux registres de qubits. L’ensemble de ces opérateurs doit constituer un jeu d’instructions suffisamment expressif pour que notre notre ordinateur puisse calculer, de façon exacte ou approchée, une classe de fonctions aussi large que possible. Il faut également pouvoir mesurer ce qubit, et l’intriquer de façon contrôlée avec d’autres qubits. Il faut enfin que tout cela « passe à l’échelle » et que notre ordinateur contienne un nombre suffisant de qubits pour effectuer des calculs utiles. Par exemple, pour factoriser un nombre de 300 chiffres en appliquant l’algorithme de Shor, il faudra de l’ordre de 2000 qubits logiques, c’est-à-dire au moins 10000 qubits physiques pour effectuer les indispensables procédures de corrections d’erreurs à chaque pas du calcul. Aujourd’hui, cela fait partie des obstacles qui semblent encore insurmontables. C’est en tout cas hors de portée de ce que la physique peut envisager à moyen terme.

Les physiciens explorent un éventail très ouvert de supports variés pour le qubit : spins d’électrons, optique, ions piégés, résonance magnétique nucléaire (RMN), jonctions Josephson, etc. Certaines approches semblent d’ores et déjà vouées à l’échec (la RMN, par exemple, passe mal à l’échelle), d’autres paraissent très prometteuses (ions piégés, par exemple).

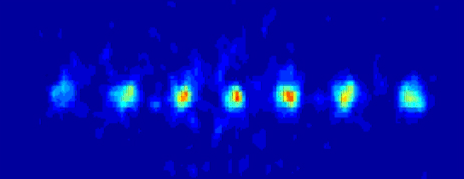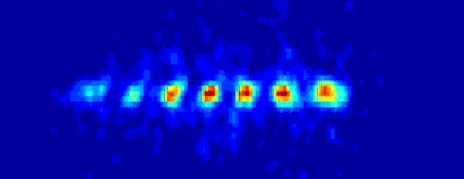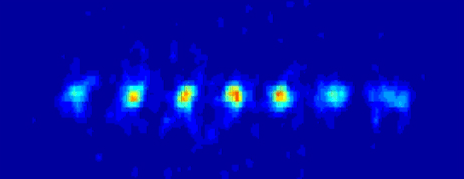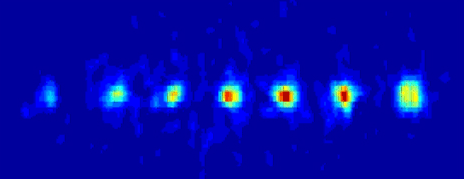
Qubits implémentés par des ions piégés.
Image : Université d’Innsbruck

On est encore loin de savoir quelles approches satisferont tous les critères. On ne sait même pas si la solution existe. Les optimistes parlent de 15 ou 20 ans, ce qui coïnciderait avec le point final d’une extrapolation de la loi de Moore, quand la quantité de matière nécessaire à un bit sera réduite à une particule. Les pessimistes disent jamais. Quoi qu’il en soit, que le chemin aboutisse ou non, on sait déjà qu’il est fertile en beaux résultats scientifique fondamentaux, en physique et en informatique, et qu’il sera jalonné d’avancées technologiques majeures, dont la première en date sera la cryptographie quantique.

6. La cryptographie quantique : c’est pour demain

D’après un dessin paru dans Physics World.

Pour expliquer les principes de la cryptographie, il est traditionnellement fait référence à deux personnages, Alice et Bob (choisis pour leurs initiales), qui souhaitent que les messages envoyés par Alice à Bob restent confidentiels. Or il est toujours possible à un observateur indiscret, traditionnellement baptisé Eve (« evesdropping » signifie indiscrétion en anglais), d’intercepter les informations qui circuleront sur les canaux de communication utilisés par Alice et Bob, quels que soient ces canaux.

La cryptographie consiste donc d’abord, pour Alice, à crypter le message confidentiel d’une façon telle qu’il soit très difficile, voire impossible à Eve d’en extraire de l’information. Elle consiste ensuite, pour Bob, à décrypter le message crypté qui lui parvient pour reconstituer le message confidentiel original. Alice et Bob doivent donc convenir à l’avance d’une méthode de cryptage-décryptage. Il y a pour cela deux grandes catégories de méthodes classiques de cryptographie : cryptographie à clé secrète, et cryptographie à clé publique.

La cryptographie quantique intervient dans le cadre de la cryptographie à clé secrète : elle va permettre à Alice et Bob de convenir d’une clé dont le secret soit garanti. Ils pourront ensuite crypter et décrypter classiquement un message en utilisant cette clé.

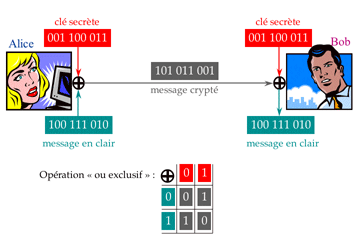
Principe du « one time pad ».

Parmi les méthodes de cryptographie à clé secrète, le « one time pad » est le seul qui garantisse une sécurité absolue. Alice et Bob se sont mis d’accord sur une suite aléatoire de 0 et de 1, la clé de cryptage, qui a la même longueur que le message qu’Alice doit transmettre à Bob. Le message crypté envoyé par Alice est le « ou exclusif », bit à bit, du message en clair et de la clé. Bob reçoit donc une suite aléatoire de 0 et de 1, vide d’information pour quiconque ne possède pas la clé, puis fait un « ou exclusif » de cette suite et de la clé, ce qui reconstitue chez lui le message en clair. Pour éviter les indiscrétions, on ne doit pas utiliser une clé donnée plus d’une fois et, surtout, la clé doit être secrète. On a donc reporté un problème crucial en amont : Alice et Bob doivent disposer d’un moyen de communication absolument sûr pour se mettre d’accord sur une clé chaque fois qu’il veulent échanger un message confidentiel.

C’est pour convenir d’une clé de « one time pad » que la physique quantique vole au secours d’Alice et Bob. À titre d’exemple, voici le protocole BB84 (Bennett et Brassard, 1984) de distribution de clé quantique. Pour constituer la clé, Alice envoie à Bob une suite aléatoire de 0 et de 1, quatre fois plus longue que la clé dont ils auront besoin. Mais chacun de ces bits est codé par un qubit qui circulera sur la ligne entre Alice et Bob. Imaginons que chaque qubit soit un photon qui peut être polarisé à 0, 45, 90 ou 135 degrés. Quand Alice doit envoyer le bit 0, elle tire à pile ou face et code ce 0 soit par un qubit à 0 degré, soit par un qubit à 45 degrés. Idem pour 1 : soit 90 degrés, soit 135 degrés. Mais Bob ne sait à l’avance ni s’il va recevoir un 0 ou un 1, ni si Alice l’aura codé dans la base standard {0,90} ou dans la base diagonale {45,135}. Il tire donc lui aussi chaque fois à pile ou face pour choisir la base, standard ou diagonale, dans laquelle il mesurera le qubit qu’il reçoit.

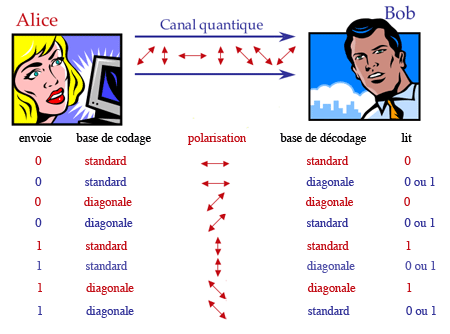
Les différentes possibilités de codage et décodage des bits codés par des photons polarisés.

Pour chaque qubit où ce choix est le même que celui d’Alice, le 0 (le 1) que Bob observe est correct à 100% : Alice avait bien codé un 0 (un 1). Mais les lois de la mesure quantique n’accordent à Bob qu’une probabilité de 50% d’observer 0 (ou 1) si Alice avait codé 0 (ou 1) dans une base différente de celle qu’il a choisie. Quand tous les bits de la suite aléatoire codés de cette manière auront été envoyés par Alice, puis reçus et observés par Bob avec 50% de chance de se tromper d’outil d’observation, Alice et Bob se disent (au téléphone, par exemple : un espionnage de cet échange ne présente plus de risque) la suite des bases qu’ils ont utilisées, Alice pour coder, Bob pour observer, sans révéler les bits codés ou observés. La probabilité de coïncidence entre le choix d’Alice et celui de Bob fait qu’ils ne retiennent alors qu’une moitié des bits, approximativement, ceux pour lesquels ils ont fait le même choix de base : cette suite de bits pourrait constituer une clé de cryptage secrète, sauf si…

… un observateur indiscret, Eve, intercepte les qubits qui passent sur la ligne, les mesure avec la même ignorance que Bob de la base de codage choisie par Alice, ce qui peut modifier le qubit si elle ne choisit pas la bonne base, puis renvoie ce qubit, éventuellement modifié, à Bob qui croit le recevoir d’Alice. Supposons qu’Alice ait envoyé un 0 codé dans la base {0,90} et qu’Eve utilise cette même base pour espionner à ce moment : elle observera un 0, puis renverra un qubit identique à Bob. Si Bob utilise lui aussi la base {0,90} pour observer ce qubit, Alice et Bob ne détecteront pas que ce bit, qu’ils conserveront, est connu par l’espionne. Mais Eve a 50% de chances de se tromper de base pour espionner, donc de renvoyer à Bob un bit codé dans une base différente de celle choisie par Alice. S’il s’agit d’un bit pour lequel Alice et Bob ont utilisé la même base, il y alors 50% de chances que Bob observe un 1 (un 0) alors qu’Alice avait codé un 0 (un 1) : si Eve espionne, 25% des bits codés par Alice et observés par Bob dans la même base seront différents.

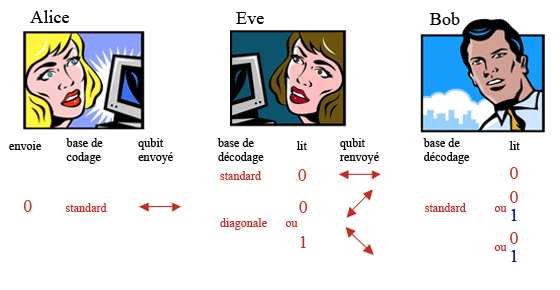
Supposons qu’Alice envoie un 0 codé dans la base {0,90} et que Bob choisisse la même base pour observer le qubit qu’il reçoit. S’ils ont été espionnés, alors le qubit observé par Bob pourra être différent de celui envoyé par Alice.

C’est pourquoi Alice et Bob se téléphonent une deuxième fois, choisissent au hasard une moitié des bits retenus à l’issue de leur premier échange, et sacrifient ces bits car maintenant ils les comparent et Eve peut écouter : s’il n’y a pas de différence, ils savent avec quasi certitude que leur clé n’a pas été espionnée (si m bits sont comparés, la probabilité qu’ils soient tous identiques malgré un espionnage est de (3/4)^m, soit 3.10^-13 pour m=100). Ils doivent évidemment tenir compte d’une ligne normalement bruitée, mais tant que le taux de différences est inférieur au taux normal d’erreurs, ils peuvent considérer que les bits restants (1/4 de la suite initiale) constituent une clé secrète, sinon ils rejettent le tout et recommencent.

Il existe d’autres protocoles que BB84 pour la distribution de clé quantique. Tous exploitent le fait que la mesure quantique perturbe l’état du qubit mesuré pour, in fine, détecter la présence d’un observateur indiscret. Ceci est impossible avec des bits classiques. On peut d’ailleurs noter que « cryptographie quantique » est un abus de langage, car rien n’est crypté, il s’agit de transmission sûre de l’information grâce aux propriétés de la matière à l’échelle quantique. Plusieurs expérimentations du protocole BB84 ont été faites, avec des transmissions sur plusieurs dizaines de kilomètres, soit par fibre optique, soit dans l’air. Un objectif majeur concerne les communications sûres entre le sol et des satellites. Quelques sociétés industrielles sont déjà sur les rangs et commencent à mettre des produits sur le marché, comme ID Quantique à Genève ou MagiQ Technologies à New York et Boston. Ce sera, à brève échéance, la première application commerciale en vraie grandeur du traitement de l’information quantique.

Pour en savoir plus, nous vous proposons, en anglais, un article à télécharger en PDF et quelques références de documents généraux sur l’information quantique.