
Algorithmes, mode d’emploi

Ada Lovelace. © Heritage images / Leemage
En 1843, un siècle avant la naissance des calculateurs électroniques, Ada Lovelace formule les premières idées fondamentales de l’informatique. Elle contribue à améliorer les premiers programmes, conçus alors sur papier.
Elle s’appelle Ada, Augusta Ada King, comtesse de Lovelace, fille du célèbre poète Lord George Gordon Byron. Certains vous diront qu’elle a juste joué un rôle de représentation publique, mais ne les écoutez pas : c’est bien grâce à elle que le premier programme informatique a été écrit (cf. dossier en ligne sur DocSciences).
Elle travaille avec Charles Babbage, mathématicien, sur la « machine analytique ». Pour faire marcher cette future machine, Ada crée des « diagrammes » qui ont pour but d’expliquer comment doit procéder la machine pour arriver au résultat recherché… et ceci indépendamment de la façon dont sont réalisées ces opérations. Ce sont des « algorithmes ».
Ada Lovelace (1815-1852) fut l’assistante de Charles Babbage (1791-1871), le mathématicien qui conçoit en 1821 le premier ordinateur. Trop difficile à réaliser uniquement avec de la mécanique, il faudra attendre un siècle pour que ce « principe » devienne réalisable. Concrètement, Ada Lovelace traduit pour Charles Babbage une conférence sur une « machine analytique » en y ajoutant de nombreuses notes. Cette machine effectuerait automatiquement des opérations abstraites pour « nous faire gagner du temps de travail, écrit-elle en 1843, et nous permettre de refaire sans étourderie des opérations que nous aurions bien définies ». Ada complète ces premiers programmes informatiques et va faire deux choses essentielles : corriger des erreurs, des « bugs », et rédiger une documentation accessible sur cette machine. Un siècle et demi plus tard, pour tous les informaticiens, ce sont encore deux terribles défis !
Pour aller plus loin, retrouvez ce sujet et celui du rôle des femmes en sciences sur DocSciences en ligne.
Le mot algorithme vient du nom du grand mathématicien perse Al – Khwarizmi (vers l’an 820) qui introduit en Occident la numération décimale (rapportée d’Inde) et enseigne les règles élémentaires des calculs s’y rapportant. La notion d’algorithme est donc historiquement liée aux manipulations numériques, mais elle s’est progressivement développée pour porter sur des objets de plus en plus complexes : des textes, des images, des formules logiques, des objets physiques…
Un algorithme, très simplement, est une méthode, une façon systématique de procéder pour faire quelque chose : trier des objets, situer des villes sur une carte, multiplier deux nombres, extraire une racine carrée, chercher un mot dans le dictionnaire… Il se trouve que certaines actions mécaniques ? peut-être toutes ! ? se prêtent bien à cette décomposition. On peut les décrire de manière générale, identifier des procédures, des suites d’actions ou de manipulations précises à accomplir séquentiellement. Décomposer chaque action en actions élémentaires pour mieux les recombiner ensuite. C’est cela, un algorithme. En tant que méthode, il répond donc à des questions du type : « Comment faire ceci ? », « Comment obtenir cela ? », « Comment trouver telle information ? », « Comment calculer tel nombre ? ». C’est un concept pratique, qui traduit la notion intuitive de procédé systématique, applicable mécaniquement, sans réfléchir, en suivant simplement un « mode d’emploi » précis.
Mais comment être sûr qu’un mode d’emploi soit rigoureusement précis ? qu’il marche vraiment dans tous les cas sans avoir besoin d’intelligence ? Il suffit de vérifier que même la chose la plus idiote au monde puisse l’utiliser. Prenons le tout premier monstre (virtuel) venu d’un jeu vidéo, appelons-le Gnirut, et voyons ce qu’il saurait faire en étant très très bête.
Le dessin ci-dessous représente Gnirut, le personnage imaginaire qui incarne dans cet article le modèle abstrait de la « machine de Turing ». Cette machine est à la fois un mécanisme et un objet algébrique qui permet d’étudier l’informatique dans ses aspects théoriques. Son principe peut facilement se résumer ainsi : elle mémorise les données – sur un ruban infini, comme cela est représenté sur le dessin – et les instructions pour manipuler ces données – sur un autre ruban. En conséquence, tout calcul ou traitement de l’information qui est mécanisable peut être programmé sur une telle machine.
D’ailleurs, nos ordinateurs ne sont que des versions de taille finie de la machine de Turing : ils sont plus efficaces uniquement parce qu’ils sont mieux intégrés. Existe-t-il d’autres technologies (biologique, quantique…) qui puissent conduire à des modèles informatiques plus riches encore ? C’est un défi scientifique qui reste à relever. Les processus mentaux de notre esprit vont-ils au-delà de tels mécanismes algorithmiques ? Autre question qui reste ouverte. Mais l’informatique conduit à se la poser de manière nouvelle et mieux formalisée.
Gnirut : le monstre testeur

Gnirut, un monstre codeur. © S. Auvin Ce personnage incarne la « machine de Turing ». Cette « machine » n’existe pas réellement, c’est un modèle qui permet d’étudier l’informatique et sur lequel se base le fonctionnement des ordinateurs.
Disons que Gnirut ne sait même pas compter jusqu’à 2 ! Il ne connaît que 0 (pour lui c’est un blanc [ ]) et 1 (pour lui c’est un bâton [I]). Au-delà, il s’embrouille. Supposons aussi qu’il ne se souvient de rien, il note tout sur un gigantesque ruban, sans limite ni à gauche ni à droite, composé de cases qui contiennent chacune un blanc ou un bâton.
Faire exécuter un algorithme à Gnirut revient à lui donner une suite finie d’instructions. Chacune de ces instructions se décompose en quatre actions élémentaires :
1) lire la case qui est devant lui ;
2) soit écrire un bâton si la case est vide ou effacer un bâton dans le cas contraire, soit ne rien faire ;
3) soit décaler le ruban d’une case vers la droite, soit vers la gauche, soit ne pas le déplacer ;
4) passer à une nouvelle instruction.
Gnirut applique chaque instruction à son ruban et passe de l’une à l’autre selon le résultat de la précédente. Il faut aussi prévoir l’instruction « Stop », sinon il continuerait sans jamais s’arrêter ! Pour Gnirut, un algorithme est l’enchaînement de ces instructions appliquées à son ruban.
Voilà ce qu’on peut demander de plus idiot à un individu (réel ou virtuel). Mais, il n’est nul besoin d’invoquer ce pauvre Gnirut imaginaire, il y a plein de manières (avec de la mécanique, de l’électronique ou même de l’optique) de construire une machine qui va pouvoir exécuter les instructions que l’on demande à Gnirut. Ces machines s’appuient sur le modèle abstrait des « machines de Turing ».
Une bête de code
Tous les informaticiens du monde sont d’accord sur le fait que Gnirut, même avec aussi peu de compétences, peut faire du codage. En effet, il peut coder des chiffres sur son ruban, par exemple en binaire : [ ][ ][ ] pour 0, [ ][ ][I] pour 1, [ ][I] [ ] pour 2, [ ][I][I] pour 3… et, en mettant suffisamment de chiffres bout à bout, il peut coder tous les nombres. Il peut aussi y coder des lettres, [ ][ ][ ][ ][ ] pour le A et ainsi de suite, jusqu’à coder des textes entiers. Il peut aussi coder des couleurs, des lignes de couleurs et, en conséquence, des images ! Les notes de musique et les mélodies ne lui échappent pas non plus ! De proche en proche il peut (avec vraiment beaucoup de blancs et de bâtons) coder tous les objets de l’univers qui l’entoure ! Ces codes n’ont rien à voir avec la réalité : ce sont juste des signes pour la représenter (Voir l’article Nom de code : binaire).
Ensuite, avec les bonnes instructions, Gnirut peut faire des opérations sur ces nombres ou ces signes.
Par exemple, « Ajouter 1 à un nombre » : c’est facile, même pour lui ! Il suffit d’abord d’aller le plus à droite du nombre, codé en binaire avec des blancs et des bâtons. Si c’est un blanc, Gnirut le transforme en bâton et il a fini. Si c’est un bâton, il le transforme en un blanc et, comme il y a une retenue, il se déplace d’un pas à gauche, il regarde le nouveau chiffre et… il applique la même règle qu’à la case d’avant ! Tout cela, Gnirut peut le faire en ayant toutes les instructions élémentaires dont il a besoin. Ensuite, en combinant les instructions précédentes, il peut aller jusqu’à 2 : il sait ajouter 1 à un nombre, donc faire une opération comme 1 1 ! Bien que Gnirut ne sache pas ce qu’est 2, il va quand même pouvoir calculer 2 en suivant les instructions. Ainsi, il est capable de faire toutes les additions. Avec d’autres paquets d’instructions, il fait des soustractions, teste si un nombre est égal à un autre… et beaucoup d’autres opérations de calcul. Voilà Gnirut au moins aussi utile qu’une calculette !
Gnirut, l’ordi… nosaure
De plus, si les blancs et les bâtons correspondent à des signes (lettres et mots, notes et mélodies, couleurs et images), c’est-à-dire si Gnirut dispose des données codées, il peut, en combinant des quantités d’instructions, mémoriser des documents, rechercher des mots dans des textes, trier, comparer, combiner… Il est en mesure de faire précisément ce que tous les ordinateurs du monde font !
Mais au fait, comment Gnirut fait-il pour se souvenir de ces instructions, pour les enchaîner, passer des unes aux autres ? Il va utiliser un deuxième ruban. Gnirut a juste à se souvenir de décaler le ruban à gauche ou à droite, d’écrire un blanc ou un bâton et de retenir le numéro de l’instruction suivante (codée elle aussi avec des blancs et des bâtons). Rien de plus facile à coder. Gnirut note alors toutes ces instructions (toujours à l’aide de blancs et de bâtons) sur un deuxième ruban qu’il n’a plus qu’à lire au fur et à mesure pour enchaîner toutes les instructions. Trop compliqué pour Gnirut me direz-vous ? Non !
Un ruban universel
En effet, pour lire ce deuxième ruban, il n’a besoin d’apprendre que quelques instructions qui lui permettent alors de trouver les instructions pour faire toutes les opérations possibles sur le premier ruban.
Finalement, Gnirut n’est pas si bête, il pourrait même être le boss de fin du jeu ! En effet, il n’y pas un calcul « mécanique », pas un « traitement automatique » que Gnirut ne sache faire avec ses deux rubans ! Quand ce n’est pas Gnirut mais un objet qui fonctionne ainsi, on parle ici de « machine de Turing universelle ».
Cela montre aussi combien calculer est un processus physique, comment les mathématiques s’incarnent quand elles deviennent algorithmes. C’est un processus physique qui marche avec ces « machines universelles à algorithmes » et il est possible que de nouvelles technologies (mécanismes biologiques, nanocalculateurs…) bouleversent complètement cette vision des algorithmes élémentaires : un sujet passionnant à suivre.
De monstrueux calculs
Tous les mathématiciens le pensent : tout ce qui est « calculable », lorsque l’on considère des nombres, ou « décidable », lorsque l’on considère des signes, peut se faire sur une machine de Turing. Ils ont « démontré » que tout ce qui est construit mathématiquement et qui correspond à ces mécanismes (fonctions calculables…) se ramène à ce que sait faire Gnirut avec ses deux rubans ! Cet état de fait s’appelle la thèse de « Church-Turing » qui « tient » depuis plus de cinquante ans. Vraiment tout ? Pas si simple. Cela peut prendre un temps énorme, « exponentiel » ! Cette difficulté se retrouve dans de nombreux problèmes « combinatoires » : il y a bien des choses que l’on peut faire en temps raisonnable, comme trier des données ou trouver le plus court chemin, mais des problèmes aussi simples que remplir au mieux un sac à dos ne pourront jamais ? c’est démontré mathématiquement ? être résolus efficacement. Il faudrait explorer presque toutes les possibilités et cela donne alors des temps de calculs vertigineux ? plusieurs siècles même avec l’électronique la plus rapide ? dès que la taille du problème augmente de beaucoup. On qualifie un tel problème de « NP-complet ». Cela peut ainsi ne jamais aboutir ! Par exemple, il est indispensable de savoir si un algorithme finit par s’arrêter ou s’il boucle indéfiniment. Un algorithme peut-il résoudre automatiquement ce problème ? Eh bien non ! Il n’existe pas d’algorithme qui puisse tester à coup sûr si un autre algorithme finit par s’arrêter ou non. Tous les algorithmes risquent de boucler indéfiniment ou de tomber dans un cas « singulier » qui provoque une erreur. Pire encore : beaucoup d’algorithmes qui seraient bien utiles pour contrôler la façon de faire des algorithmes n’existent pas !
Finalement Gnirut et ses deux rubans n’ont pas fini de nous faire cogiter. Surtout que les mathématiciens ont bien démontré que tous les ordinateurs du monde ne sont que des machines de Turing qui peuvent exécuter en une fois des gros blocs d’instructions. Mais leur mémoire est finie, contrairement aux rubans de Gnirut.
Les talents cachés de Gnirut
En attendant que les informaticiens aient fini de comprendre ces problèmes, essayons de faire des choses utiles avec les machines de Turing :
- programmer un robot pour qu’il sorte d’un labyrinthe (par exemple en le faisant toujours aller à droite sans jamais qu’il ne revienne sur son parcours) ;
- chercher un mot dans le dictionnaire ;
- trouver le chemin le plus court d’un point à un autre (par exemple en simulant un groupe de personnes qui à chaque carrefour se sépare en deux, pour explorer toutes les combinaisons… le premier arrivé prévenant tous les autres) ;
- tester si un théorème mathématique est exact (en générant toutes les formules exactes possibles à l’aide des règles de la logique, des formules de plus en plus longues et en regardant si la formule recherchée apparaît) ;
- simuler des phénomènes naturels, comme la météo de la semaine à venir, ou contrôler des systèmes comme un moniteur cardiaque ou un avion de ligne…
Pour chercher un mot dans un dictionnaire, sans aucune information sémantique, ne première méthode est de tourner les pages une à une. S’il y a 1 000 pages, il faut entre 1 et 1 000 gestes suivant que le mot commence par A ou Z. Cela est fastidieux, mais de cette façon on est sûr de ne pas manquer le mot recherché.
Les informaticiens savent faire mieux : ouvrir le dictionnaire en son milieu ; si le mot est situé avant le milieu, ne considérer que la première moitié des pages, s’il est situé après, ne considérer que la deuxième moitié ; ouvrir le dictionnaire au milieu de la moitié des pages considérées ; répéter le procédé jusqu’à ce qu’il ne reste qu’une page. Que se passe-t-il ? À chaque fois, on ne considère que la moitié des pages, donc 1 000, 500, 250, 125, 63, 32, 16, 8, 4, 2, 1 page… et hop le mot est trouvé ! en 10 étapes au lieu de 1 000 ! Voilà un bel algorithme, « optimal », on ne peut pas être plus efficace, et qui « converge », diviser sans cesse le nombre de pages ne peut que finir par donner 1. Presque tous les algorithmes de recherche sont construits sur de tels mécanismes.
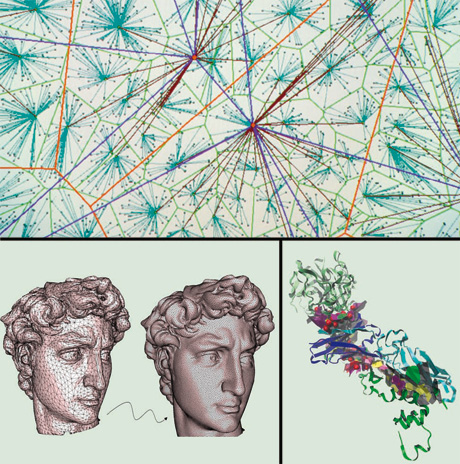
Un algorithme pour trois applications.
© INRIA / TREC / GEOMETRICA / DocSciences
Qu’ont en commun ces trois images ? Elles résultent du même type de calcul ! En effet, c’est le même algorithme qui a permis de représenter des réseaux informatiques (en haut), un objet en trois dimensions (à gauche) et une protéine (à droite).
L’image du haut est une représentation de grands réseaux de communication. Cette représentation plane permet de simuler les performances d’un réseau avant sa construction et d’optimiser sa conception. En-dessous, à droite, se trouve une autre modélisation géométrique qui, elle, simule les contacts entre deux protéines en présence d’un virus. Elle permet de comprendre les relations entre l’architecture biologique et la fonction correspondante. Enfin, la représentation de la statue en trois dimensions résulte d’un calcul qui permet de manipuler, stocker et transmettre les données concernant la surface d’un objet réel.
Ce qui est remarquable ici, est que ces trois constructions numériques résultent du même algorithme, la triangulation de Delaunay/Voronoï. Il permet ainsi d’étudier virtuellement des objets très différents. Sans son efficacité, les calculs sur ces avatars numériques seraient trop lourds à mener. Cette triangulation a bien d’autres applications, elle permet, par exemple, de générer la trajectoire d’un robot.
Il n’est pas question de redonner à chaque fois toutes les instructions élémentaires, nous ne nous en sortirions pas ! Comment faire ? Il existe deux méthodes efficaces. Gnirut sait faire une addition. Convenons avec lui que si on dit : « Additionner A et B. », il copie le nombre A sur son ruban, tout comme le nombre B, puis il enchaîne toutes les instructions pour que la somme A B s’inscrive aussi sur son ruban. Nous avons défini la fonction « addition » et pouvons désormais concevoir des algorithmes sans revenir à de tels détails. On fait de même avec toutes les opérations susceptibles d’être utilisées : multiplier, comparer, trier… mais aussi : afficher une image, tracer une droite, jouer une note de musique… On définit la fonction et ses paramètres, par exemple : « Jouer do pendant 1 seconde. » où la note (do) et sa durée (1 seconde) sont des paramètres. Une fois défini « Jouer une note pendant une durée. » avec d’autres fonctions elles-mêmes définies avec d’autres fonctions… jusqu’aux instructions élémentaires elles-mêmes déjà définies (sur le ruban), nous allons pouvoir les combiner et… jouer de la musique.
Comment organiser ces fonctions pour faire des choses de plus en plus complexes ? C’est très simple. Il y a trois grandes idées : combiner les fonctions, introduire des choix, des branchements, et utiliser des boucles ou des définitions récursives. Ainsi on peut décrire de manière prodigieusement concise tous les algorithmes.
Pour bâtir des algorithmes, on utilise trois grands principes.
Combiner les fonctions : faire ci puis ça. Par exemple, pour additionner A, B et C : « Additionner A à B. », puis « Additionner le résultat à C. » Voilà, l’addition de trois nombres est définie à partir de celle de deux nombres.
Introduire des branchements : si ceci alors cela. Ce principe permet d’exécuter en fonction de paramètres. Par exemple : « Diviser A par B. » est impossible si B = 0. Alors un « bon » algorithme aura la forme : « Si B ≠ 0 alors faire la division. Si B = 0 alors arrêter le calcul. ». On parle de « pseudo-code » pour ces façons concises de spécifier des instructions, « Si B = 0 alors stop, sinon (A / B). ». Ici la construction « si… alors… sinon… » décrit le branchement.
Utiliser des boucles et des récursions : pour jouer les 10 000 notes d’une mélodie, inutile d’écrire 10 000 instructions, une seule suffit :
« Jouer à partir de la note n : jouer la note n puis jouer à partir de la note n + 1, si elle existe. » Cette instruction « récursive », qui se rappelle elle-même, définit la « boucle d’instructions ».
Ce sont les langages informatiques qui permettent de « mettre en musique » ces mécanismes… grâce à la programmation.
Pour aller plus loin, nous vous proposons quelques références bibliographiques.
- Delahaye J.-P., Complexités. Aux limites des mathématiques et de l’informatique, coll. « Bibliothèque scientifique », Belin – Pour la science, 2006.
- Dewdney A. K., The (New) Turing Omnibus. 66 Excursions in Computer Science, Holt Rinehart and Winston, 2003.
- Hernet P., Les Algorithmes, coll. « Que sais-je ? », n° 2928, Puf, 2002.
- Le langage mathématique et les langages de programmation, par G. Dowek, document téléchargeable en PDF.
Cet article est paru dans la revue DocSciences n°5 Les clés de la révolution numérique, éditée par le CRDP de l’Académie de Versailles en partenariat avec l’INRIA.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !
