
La programmation par contraintes
Supposons qu’on veuille organiser la rotation des avions dans un aéroport, en optimisant l’utilisation des pistes, l’emploi du temps du personnel navigant, l’attente des voyageurs, l’acheminement des bagages, etc. Pas question que deux atterrissages se suivent à moins d’une minute ! Ni qu’un atterrissage et un décollage aient lieu en même temps sur la même piste ! On exigera aussi que les avions d’une même compagnie ou à destination d’un même continent partent toujours du même terminal, que chaque avion puisse être ravitaillé avant de redécoller, mais sans rester plus d’une heure au sol, que les temps de travail légaux soient respectés pour chacun, etc. Avec de si nombreuses contraintes, comment trouver en pratique une solution – et la meilleure possible – à ce type de problèmes ?
Tout est dans l’approche
Selon l’approche traditionnelle en informatique, il s’agirait de rechercher un algorithme général (écrit dans un langage tel que le C, Pascal ou Java) capable de résoudre le problème et de s’adapter facilement si on rajoute un vol, par exemple, ou si on supprime une compagnie. Mais on peut aussi envisager une autre solution, utilisant un paradigme issu de la programmation logique et de la Recherche Opérationnelle : la programmation par contraintes. Grâce à elle, le programme informatique résolvant notre problème peut s’écrire de manière très simple, presque comme on l’énoncerait dans le langage naturel. Il s’agit simplement d’écrire, les unes après les autres, les différentes contraintes que l’on souhaite voir respectées… et l’ordinateur se débrouille tout seul !
Déplacer la difficulté
Il n’y a pourtant pas de miracle, et la difficulté intrinsèque du problème doit bien se retrouver quelque part. En fait, le gros du travail a été réalisé en amont, dans la conception même du langage « de haut niveau » utilisé à cet effet : l’algorithmique se situe essentiellement dans les « solveurs » qui permettent d’interpréter le langage utilisé en une suite d’opérations-machine. Il s’agit, comme l’on dit, de « propager les contraintes », c’est-à-dire en quelque sorte de les agglomérer les unes aux autres pour découvrir quelles sont leurs implications conjointes, et ainsi réduire de plus en plus l’espace des paramètres à ajuster (comme les heures de décollage et l’attribution des diverses ressources, vol par vol…). Parallèlement, des algorithmes spécifiques s’intéressent à la manière optimale d’explorer l’arbre des possibilités, ce qui consiste en quelque sorte à décider par quel bout il vaut mieux prendre le problème – le but du jeu étant d’éliminer le plus rapidement possible tout un ensemble de directions de recherche dans lesquelles on peut s’apercevoir très vite qu’il n’y aura pas de solutions.
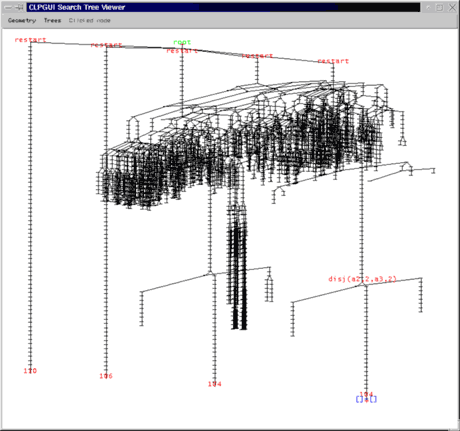
Visualisation 3D de l’arbre de recherche développé dans un problème d’optimisation (ordonnancement disjonctif de 50 tâches, 4000 nœuds) avec l’outil CLPGUI).
L’avantage de la programmation par contraintes, c’est que le travail fait une fois pour toutes au niveau des solveurs peut être réutilisé dans des situations extrêmement diverses. Si on veut rajouter une contrainte – ce qui revient en principe à formuler un autre problème, ayant d’autres solutions – inutile de chercher un nouvel algorithme et de réécrire tout le programme ! Il suffit le plus souvent d’ajouter une seule ligne : celle qui décrit la contrainte en question !
À chaque problème sa solution
Cette technique, extrêmement puissante, peut s’appliquer à des problèmes très divers : attribution de ressources, ordonnancement de tâches, rotation de personnels, gestion d’emplois du temps… Dans un cadre scolaire, par exemple, on obtiendra très vite une solution en imposant des contraintes du type « jamais une classe sans professeur », « jamais deux professeurs en même temps pour la même classe », ou « deux classes dans la même salle », etc. À chaque fois, le programme se présente comme une suite d’énoncés qui sont la traduction directe des contraintes requises par le programmateur, ce qui rend l’ensemble non seulement élégant, simple et naturel, mais également très facile à lire ! D’un point de vue pratique, il faut noter que si la programmation par contraintes a donné lieu au développement de langages spécifiques, l’algorithmique sous-jacente peut en réalité s’écrire – se traduire – dans n’importe quel langage. Son utilisation la plus répandue dans le monde industriel se fait aujourd’hui en C , grâce à des « bibliothèques » qui sont des sortes de ponts entre ce langage et le paradigme des contraintes.
Pour étendre encore le champ de ses applications industrielles et commerciales, les recherches se poursuivent pour mettre au point de nouveaux solveurs, mais aussi sur la visualisation des étapes d’exécution. Car dans ce type de programmes, les contraintes sont traitées conjointement et la solution n’émerge qu’à la fin. Comment suivre, alors, le déroulement du programme et déceler une éventuelle erreur ? D’importantes recherches sont ainsi menées afin d’accroître les possibilités de débogage, d’inspection et d’optimisation des programmes. Mais d’ores et déjà, après un développement rapide depuis une quinzaine d’années, la programmation par contraintes fait l’objet d’applications courantes très diverses, même si elle demeure peu connue des milieux non spécialisés… et même si beaucoup utilisent ses résultats sans le savoir !
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !
