Des calculateurs universels
Dans un premier document, Le calcul, une notion difficile à attraper, nous avons vu qu’il avait fallu attendre la première moitié du 20e siècle pour que la notion de calcul soit formalisée et étudiée pour elle-même. À cette époque, quatre définitions différentes ont été proposées, qui essayent de capturer ce qu’est un calcul effectué automatiquement par une machine.

Alan Turing © Beryl Turing.
Mais la diversité des réponses n’est qu’apparente : les quatre définitions sont équivalentes, en ce sens que ce qui peut se calculer par l’une peut aussi, modulo un codage, se calculer par une autre.
C’est à partir de sa définition du calcul, qui se fonde sur une machine abstraite que l’on appelle depuis la machine de Turing, que Alan Turing établit deux résultats fondamentaux. Le premier nous dit que tout n’est pas calculable : il existe des problèmes dont la solution ne peut se calculer par un algorithme, il existe des fonctions dont on ne peut pas calculer l’image en un point par un ordinateur, il existe des prédicats qu’on ne peut vérifier par un calcul. Ce résultat négatif ne doit donc pas nous amener à baisser les bras : il exprime simplement que si on fixe précisément ce qu’est un calcul, alors on fixe aussi ce que l’on peut calculer dans ce cadre. Et donc, comme tout grand résultat négatif, il ouvre un nouveau continent, l’algorithmique ou science de ce que l’on peut calculer, que les informaticiens se sont empressés de venir habiter et explorer.
Il existe une machine universelle !
Mais c’est le second résultat de Turing qui va nous intéresser ici. Dès son premier article sur le sujet, Alan Turing énonce qu’il existe une machine universelle. Les conséquences de cette idée sont gigantesques et ont véritablement transformé notre monde.
Pour expliquer pourquoi, il faut en savoir un peu plus sur le fonctionnement des machines de Turing. Vous pouvez voir une explication animée de ces machines sur la page Machine de Turing. Il nous suffira de retenir qu’une machine de Turing est composée d’un ruban et d’une unité qui contrôle une tête de lecture/écriture capable de se déplacer sur ce ruban. Nous désignerons une machine de Turing en notant ces deux ingrédients entre crochets :
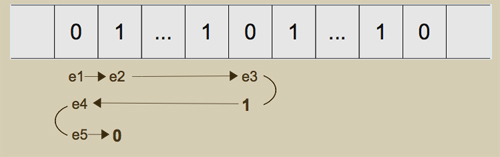
Le ruban, aussi long que nécessaire, est divisé en cases sur lesquelles sont imprimés des symboles (appartenant à un alphabet fini). Une tête de lecture/écriture se déplace sur ce ruban de case en case. Elle est capable de lire le symbole de la case courante, écrire un symbole dans la case courante et peut se déplacer d’une case vers la droite, vers la gauche ou rester sur place. Le comportement de la tête est dicté par l’unité de contrôle qui possède un état interne (il y a un nombre fini d’états internes possibles). L’état interne indique ce que doit faire la tête de lecture/écriture à la lecture d’un symbole donné sur le ruban : il faut écrire un symbole (lequel), se déplacer (dans quelle direction) et changer d’état interne (lequel). Tout cela peut se définir par un tableau, comme celui ci-dessous. Le résultat du calcul est l’état du ruban quand la machine s’arrête.
 |
||||
| ancien état | symbole lu | symbole écrit | mouvement | nouvel état |
|---|---|---|---|---|
| e1 | 0 | 0 | droite | e2 |
| 1 | erreur | |||
| e2 | 0 | 1 | gauche | e3 |
| 1 | 1 | droite | e2 | |
| e3 | 0 | 0 | droite | e4 |
| 1 | 1 | gauche | e3 | |
| e4 | 0 | erreur | ||
| 1 | 0 | droite | e5 | |
| e5 | 0 | erreur | ||
| 1 | 1 | stop | – | |
Ce tableau représente le contrôle d’une machine de Turing qui additionne deux nombres écrits en unaire sur le ruban de la machine, et séparés par un zéro. Un nombre n écrit en unaire correspond à une suite de n symboles 1 successifs sur le ruban. Par exemple, pour additionner 2 et 3, on écrit 01101110.
Le contrôle détermine les actions de la tête de lecture/écriture qui se déplace sur le ruban. L’idée du calcul est de se déplacer vers la droite jusqu’à rencontrer le premier 0 et de le remplacer par un 1. La tête se déplace alors vers la gauche jusqu’à rencontrer le 0 initial. Elle se déplace alors à nouveau vers la droite pour effacer le premier 1 qu’elle rencontre.
Il est important de remarquer que le contrôle de la machine est fixé une fois pour toutes et s’identifie donc avec la machine elle-même. Une machine de Turing est une machine abstraite, mais s’il fallait la construire, le contrôle correspondrait à une structure fixe. La seule partie variable de la machine est constituée des symboles écrits sur le ruban qui peuvent changer au cours de l’exécution :
Le résultat établi par Alan Turing est le suivant : il existe une machine de Turing MU qui est dite universelle car elle est capable de simuler l’exécution de toutes les autres machines de Turing. Simuler une machine quelconque T veut dire ici qu’il suffit de fournir à la machine universelle :
- la description du contrôle de T (en l’écrivant dans un certain format sur le ruban de MU),
- et les données en paramètres du calcul (ailleurs sur le ruban de MU),
pour que MU se comporte comme la machine T : quand elle s’arrête, elle laisse le ruban dans l’état où T l’aurait laissé à son arrêt. Autrement dit, avec notre notation :
Si l’on réfléchit un peu, ce résultat est surprenant : il dit qu’au lieu de considérer une variété infinie de machines différentes (des additionneurs qui font des additions, des multiplieurs qui font des multiplications, des horloges qui calculent la date et l’heure du jour, des astrolabes qui calculent la position des étoiles, des machines à calculer l’heure des marées, etc.), il suffit de considérer une seule machine, qui peut faire tous les calculs, pourvu qu’on lui fournisse une description adéquate de la tâche à exécuter. Cette description, c’est une représentation du contrôle du calcul à effectuer et dans la suite, nous l’appellerons un programme.
Il ne faut pas croire que les machines universelles soient intrinsèquement plus compliquées que les autres. Elles peuvent être même très simples. Par exemple, en 2007, Alex Smith (un étudiant de l’Université de Birmingham) a construit une machine de Turing (c’est-à-dire qu’il a spécifié une unité de contrôle) à seulement deux états, agissant sur 3 types de symboles, et qui est universelle. C’est une machine très simple et dont la description est très petite ! (Cependant, la notion d’universalité utilisée n’est pas exactement la notion d’universalité habituelle, et elle requiert de préparer éventuellement un ruban infini.)
D’autres machines ou d’autres processus, qui n’ont pas du tout été pensés pour être des calculateurs universels, se révèlent en être. Par exemple, le jeu de la vie, initialement proposé en 1970 par le mathématicien britannique John Horton Conway comme un simple jeu sur un damier, exhibe des comportements d’une surprenante complexité, en dépit de la simplicité de ses règles. En fait, chaque case du damier est habitée par une cellule vivante ou morte et en choisissant bien la configuration initiale de ce damier, on peut simuler le fonctionnement d’une machine de Turing arbitraire.
Ce qu’il faut en retenir, c’est que l’universalité n’est pas une propriété très spéciale chez les machines et qu’il y a beaucoup de dispositifs qui sont des calculateurs universels.
Un détour par la Reine Christine de Suède

Christine de Suède en conversation avec René Descartes. Détail d’une peinture de Louis Michel Dumesnil. Photo © RMN (château de Versailles) – Hervé Lewandowski.
En définissant ce qu’est un calcul, Alan Turing est amené à distinguer contrôle et données. Mais pour avoir la notion la plus générale possible de calcul, il faut que le contrôle puisse aussi être vu (parfois) comme une donnée. Cette idée peut sembler se réduire à une astuce technique qui permet d’exhiber une machine à calculer qui a des propriétés particulières. Elle a pourtant des conséquences pratiques considérables sur lesquelles nous reviendrons ci-dessous. Elle a aussi des conséquences épistémologiques et permettra à John von Neumann de répondre à un défi lancé au 17e siècle par la reine Christine de Suède à René Descartes.
Le corps est une machine
René Descartes (1596 – 1650) pense en effet comprendre la vie en comparant les organismes à une machine : on peut expliquer les principales fonctions corporelles – la digestion, la locomotion, la respiration, mais aussi la mémoire et l’imagination – comme si elles résultaient d’un automate, à l’image d’une horloge destinée à montrer les heures par la seule disposition de ses roues et contrepoids. Mais la Reine Christine de Suède, que René Descartes essaya de convaincre, lui rétorqua qu’elle y croirait quand il lui aurait montré comment une horloge peut se reproduire…
Un siècle plus tard, en 1739, Jacques de Vaucanson (1709 – 1782) présente à l’Académie des Sciences un automate fameux, le « Canard Digérateur », un chef-d’œuvre de simulation anatomique comptant plus de 400 pièces en mouvement reproduisant les principales fonctions vitales (respiration, digestion, locomotion) : l’animal battait des ailes, mangeait du grain et déféquait (les grains étaient digérés par dissolution). Mais si les automates de Vaucanson imitaient les grandes fonctions physiologiques, ils ne pouvaient toujours pas se reproduire.

Réplique du canard de Vaucanson. © Musée des automates de Grenoble. L’automate original a été perdu.
Voltaire a décrit Vaucanson par ces vers :
« Le hardi Vaucanson, rival de Prométhée,
Semblait, de la nature imitant les ressorts,
Prendre le feu des cieux pour animer les corps. »
Il fallut attendre John von Neumann et les années 1950 pour obtenir une réponse convaincante : oui, une machine peut effectivement construire une copie d’elle-même : s’auto-répliquer.
John von Neumann
John von Neumann (1903 – 1957) est un mathématicien hongrois émigré aux États-Unis. Il contribua de manière majeure à de nombreux domaines comme la mécanique quantique, la théorie des ensembles et l’analyse numérique, et en créa d’autres comme la théorie des jeux.
En 1945, John von Neumann fut appelé comme consultant sur le projet EDVAC. Les États-Unis avaient besoin de grands moyens de calcul pour soutenir l’effort de guerre et le projet EDVAC faisait suite au calculateur ENIAC. Le programme à exécuter n’était pas enregistré dans la mémoire de l’ENIAC mais devait être câblé manuellement. Ses concepteurs, John Mauchly et Presper Eckert, virent tout l’intérêt d’enregistrer le programme dans la mémoire centrale de la machine, au même titre que les données sur lesquelles il travaille, et proposèrent cette architecture pour la nouvelle machine. Von Neumann, qui avait rencontré Turing en 1936-37 lorsque ce dernier séjourna à Princeton, insista sur ce point dans son rapport sur l’EDVAC. Ce rapport fut largement diffusé et l’architecture correspondante fut baptisée architecture de von Neumann. Dans les grandes lignes, cette organisation est toujours celle de nos ordinateurs actuels.
La réponse de von Neumann
Pour répondre à la question de la Reine Christine, il faut précisément définir ce qu’on entend par « machine » et ce qu’on entend par « reproduction ». Pour von Neumann, qui a sur ce point une approche très fonctionnaliste, le mécanique est in fine ce qui peut être réduit à un programme d’ordinateur et la reproduction correspond à dupliquer ce programme.
L’objectif de von Neumann était clairement de montrer que les processus du vivant sont réductibles à des processus mécaniques, décrits par des opérations pouvant être exécutées de manière autonome, sans l’aide d’un « cornac caché » : une machine comme l’entend Turing. Pour von Neumann, comme pour la Reine Christine, la reproduction et le développement sont une caractéristique spécifique du vivant. Mais pour von Neumann, cette caractéristique est juste une propriété particulière possédée par certaines machines, et non pas une qualité transcendant les processus physiques pour donner un statut particulier aux processus biologiques. L’existence d’une machine, d’un ordinateur, capable de reproduction, est donc un élément de réponse crucial dans un débat fort ancien opposant le statut de la biologie à celui de la physique.
Von Neumann ne va pas s’appuyer sur les machines de Turing pour montrer qu’un calcul peut s’auto-répliquer. Il utilisera un autre modèle de calcul qu’il va inventer à la fin des années 1940 : les automates cellulaires (qui bien sûr ne calculent pas plus de choses qu’une machine de Turing).
Nous pouvons donner une idée simplifiée de sa construction en utilisant notre notation et en suivant un exemple développé par Bernard Chazelle. Considérons le calcul suivant :
Ce calcul consiste à appliquer un certain programme à lui-même. Le programme est donc vu à la fois comme un calcul à effectuer (quand il est à gauche et vu comme du contrôle) ou comme une donnée (quand il est à droite). Le résultat de ce calcul qui fait référence à lui-même, est simplement :
Ce résultat est presque ce que l’on veut obtenir : il manque nos crochets, qui permettent de savoir où débute et où s’achève la description d’un calcul, et notre barre de séparation, qui permet de savoir quand un objet doit être vu comme un programme ou bien comme une donnée. La correction est facile et l’exécution du programme suivant fournit une copie de lui-même :
Autre exemple, un robot modulaire auto-réplicateur tridimensionnel a été réalisé physiquement en 2005 par Hod Lipson, Viktor Zykov, Efstathios Mytilinaios et Bryant Adams à l’Université de Cornell. Un module prend la forme d’un cube articulant deux parties le long d’un plan diagonal. Les modules se lient les uns aux autres par électro-aimantation.

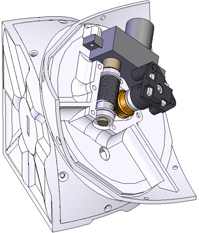
Robot modulaire auto-réplicateur. Un module prend la forme d’un cube articulant deux parties le long d’un plan diagonal. À droite, le schéma de son mécanisme.
© Cornell University.

Robot modulaire auto-réplicateur. Les cubes se lient les uns aux autres par électro-aimantation.
© Cornell University.
Les photos suivantes illustrent le processus d’auto-réplication d’un robot composé de 4 modules. Ce processus, qui nécessite 2,5 minutes, se fait sans autre intervention humaine que la mise en place de nouveaux modules à des places localisées (cerclées en rouge sur les photos) que le robot en cours de réplication vient chercher afin de les intégrer à la nouvelle structure. Un film du processus complet est visible sur le site de l’Université de Cornell.

Robot modulaire auto-réplicateur. Vues successives du processus.
© Cornell University.
Notons qu’une machine n’a pas besoin d’être universelle pour se répliquer. Mais cette capacité repose de manière cruciale sur la possibilité de regarder le même objet parfois comme un calcul à effectuer et parfois comme des données (y compris des données de ce même calcul). L’autre ingrédient nécessaire est le « deux fois » : il faut pouvoir itérer un calcul. Ces deux notions, la dualité programme/données et l’itération, sont si fondamentales que l’on peut dire que l’informatique naît comme domaine scientifique avec l’étude de ces notions.
L’ADN et le code génétique
En avril 1953 paraît l’article de James Watson et Francis Crick élucidant la structure du code génétique. L’ADN est constitué de deux brins complémentaires. Chaque brin est constitué d’une suite de nucléotides notés A, T, C et G. Le nucléotide A est toujours apparié à T et G à C :
T A G C A G C T A G C A G C…
La structure en brins complémentaires n’apporte pas d’information supplémentaire par rapport à un seul brin. Mais elle permet un mécanisme simple de copie de l’ADN : les deux brins se séparent et les nucléotides libres disponibles dans l’environnement viennent s’apparier aux deux brins simples pour reconstituer deux molécules identiques d’ADN.
L’ADN correspond donc à la donnée d’un processus de copie. Ce processus de copie est réalisé par la machinerie cellulaire qui, en partie, est constituée par des protéines. Ces protéines sont codées par certaines séquences de nucléotides sur l’ADN : les gènes. C’est la machinerie cellulaire elle-même qui « lit » les gènes sur l’ADN et les interprète pour construire ces protéines. L’ADN joue donc à la fois le rôle de données (on le duplique) et de programme (il dicte les protéines à construire). En oubliant la structure en double brin, et en simplifiant brutalement, on peut donc écrire :
Même si notre présentation est caricaturale (tout n’est pas codé dans le génome par exemple), elle est correcte dans les grandes lignes. La dualité programme/données et l’itération sont donc présents d’une façon cruciale au cœur du vivant !
Les ordinateurs nous envahissent
Mais revenons aux calculateurs et au calculateur universel. L’idée géniale de Turing est de considérer que l’unité de contrôle d’une machine à calculer peut être vue comme une donnée pour une autre machine à calculer : programmes et données sont traités sur le même pied d’égalité grâce à la machine universelle.

La machine universelle est capable de réaliser tous les traitements possibles sur toutes les représentations numériques. © Yudesign | Dreamstime.com.
Cette idée est géniale car elle ouvre la voie au développement des ordinateurs : au lieu de construire physiquement une machine pour chaque type de calcul, il suffit de construire une machine universelle et de lui donner le programme voulu. Elle fera le même calcul que la machine spécialisée, elle ira sans doute un peu moins vite, elle utilisera sans doute un peu plus de mémoire (de longueur de ruban), mais elle arrivera au même résultat tout en évitant de construire autant de machines spécialisées qu’il y a de type de calculs à effectuer.
Et c’est ce qui a été fait : tous nos ordinateurs sont des machines universelles. Le supercalculateur utilisé pour les prévisions météorologiques, mon ordinateur portable et le processeur embarqué dans mon lecteur de MP3 sont capables de faire les mêmes calculs, même si ce n’est pas à la même vitesse ou s’il manque de mémoire. Car il est bien plus simple de construire une machine universelle et de la programmer que de construire une machine spécialisée pour chaque besoin. Le contrôle d’une machine universelle est relativement simple : il consiste à interpréter les ordres du programme (qui sont écrits sur le ruban) et agir en accord sur les données (qui sont aussi sur le ruban). Cela peut se faire avec quelques dizaines d’états internes : le premier microprocesseur complet sur une seule puce, le I4004 construit par Intel, ne comportait que 2300 transistors.
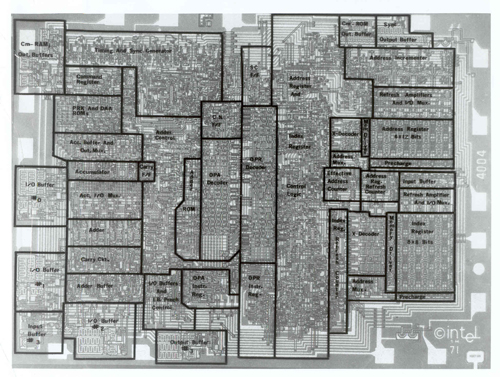
I4004 : premier processeur complet (4 bits) sur une seule puce. Ce processeur comportait 2300 transistors. Il correspond à l’unité de contrôle d’une machine universelle.
© Intel Corporation.
Nos ordinateurs sont en fait un peu plus compliqués, afin d’être plus efficaces. Par exemple, au lieu de se déplacer de case en case sur le ruban, on se permet de sauter d’une case à une autre case arbitraire grâce à une adresse (il faut numéroter les cases du ruban). On ne parle plus de ruban (d’une machine de Turing) mais de mémoire (d’un ordinateur). Cela ne change rien à ce que l’on peut calculer, mais cela permet d’aller plus vite.
Nos ordinateurs, contrairement à la machine abstraite de Turing, ne disposent pas d’une mémoire « aussi grande que nécessaire » : leur capacité mémoire est limitée par notre technologie. Et même si aller plus vite ne change rien en principe à ce que l’on peut calculer, en pratique, il est important de disposer du résultat d’un calcul sans attendre trop longtemps.
Par exemple, la prévision météo est faite en simulant l’évolution de l’atmosphère par un calcul : on ne peut donc faire de prédiction que si la simulation « va plus vite » que le phénomène naturel. Les technologies utilisées pour construire physiquement la machine universelle ont donc un impact considérable. Or depuis les années 50, nos capacités technologiques ont à peu près doublé tous les deux ans pour un prix décroissant.
Cette constatation a été faite par Gordon Moore, l’un des fondateurs d’Intel. En 1965, en étudiant l’évolution des technologies utilisées pour construire les ordinateurs (d’abord des tubes à vide et des mémoires en ferrite, puis des transistors sur des circuits imprimés jusqu’à l’apparition des premiers circuits intégrés) il se rend compte de cette croissance exponentielle et postule qu’elle se poursuivra. Cette loi de Moore est vérifiée jusqu’à nos jours.
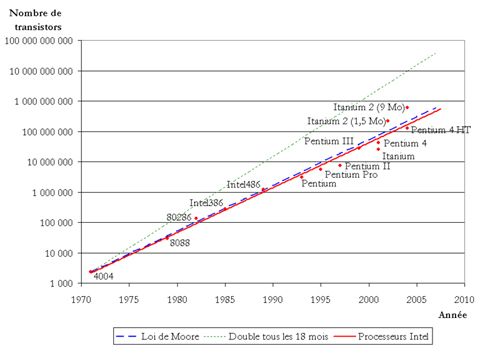
Graphique illustrant la loi de Moore. Ce graphique (en ordonnées logarithmiques) illustre la loi de Moore par rapport à l’évolution réelle du nombre de transistors dans les microprocesseurs Intel ; en pointillés verts au-dessus, représentation de l’hypothèse selon laquelle ce nombre doublerait tous les 18 mois. Source : Wikipédia.
Depuis les années 70, une grande partie de cette croissance exponentielle est due à la miniaturisation et à l’intégration toujours plus grande des transistors dans les circuits électroniques. Ce sont les transistors qui permettent de construire les mémoires et les unités de contrôle qui constituent nos ordinateurs. Plus les transistors sont petits, plus ils sont rapides (car l’électricité les traverse sur une plus courte distance, leur capacité est plus faible et l’énergie qu’ils consomment est plus petite : ils peuvent donc fonctionner à une fréquence plus élevée). Les ingénieurs d’Intel ont calculé que nos transistors actuels sont suffisamment petits pour en faire tenir 200 millions sur la tête d’une épingle et que le prix d’un transistor ne revenait pas plus cher que celui d’un caractère imprimé dans un journal de grande diffusion.
Un dernier exemple montre l’extraordinaire croissance des techniques permettant de construire nos ordinateurs. En 1978, un billet d’avion sur un vol commercial Paris – New York revenait à 900 $ et le voyage durait 7 heures. Si la loi de Moore s’appliquait aux voyages en avion comme elle s’applique à l’industrie des semi-conducteurs, un vol Paris – New York reviendrait aujourd’hui à 1 centime d’euro et prendrait moins d’une seconde.
Le monde numérique
Les progrès technologiques de l’industrie des semi-conducteurs et les avancées faites dans le domaine du logiciel au fur et à mesure que l’on comprend mieux ce que sont les programmes, ces objets nouveaux et étranges, ont permis la diffusion de l’informatique et créé pour chacun de nouveaux espaces à habiter et de nouvelles activités humaines : le monde numérique. Le web, les réseaux sociaux ou les blogs sont des exemples de ces nouveaux espaces à habiter. Mais le monde numérique ne se déploie pas qu’à travers des espaces autonomes et indépendants de notre monde physique. Il vient s’entrelacer intimement avec nos objets les plus usuels.
Par exemple, nous avons mentionné le lecteur de MP3 dans la liste des calculateurs universels. On parle d’informatique enfouie pour désigner ces ordinateurs que nous ne voyons pas mais qui calculent dans nos machines à laver, nos appareils photos, nos voitures, nos téléphones, nos GPS, nos maisons…
Mais pourquoi trouve-t-on des ordinateurs partout ? Et que calcule un lecteur de MP3 ? Après tout, on ne considère pas que le tourne-disque de papa qui permet d’écouter les disques microsillons calcule le son qu’il émet via les haut-parleurs. Alors pourquoi considérerait-on qu’un lecteur de MP3 calcule ?

Si mon lecteur de MP3 est un calculateur universel, qu’en est-il de mon tourne-disque ?
Source des images : Wikipédia (tourne-disque, lecteur MP3, ordinateur portable).
Le tourne-disque de papa est pourtant un calculateur analogique : les rugosités du sillon du disque vinyle font vibrer le diamant de la tête de lecture. Le courant produit par effet piézo-électrique est amplifié avant d’être transformé en son par les haut-parleurs. Pour l’électronicien qui conçoit l’amplificateur, le tourne-disque se réduit bien à un calcul : il s’agit de multiplier par un certain coefficient le signal en entrée fourni par le diamant avant de le transmettre aux haut-parleurs. Mais ce calcul est toujours le même. Par ailleurs l’électronicien ne peut s’abstraire des caractéristiques du signal en entrée. Ce n’est pas un nombre abstrait qui varie au cours du temps : c’est une tension et le dispositif qu’il doit concevoir doit multiplier des tensions électriques. Qu’il se retrouve devant le problème de multiplier des fréquences plutôt que des courants, et il devra concevoir un circuit entièrement nouveau, alors qu’il s’agit du même problème abstrait. Considérer le tourne-disque comme un calculateur n’apporte rien : c’est une machine tellement spécialisée qu’elle n’exécute qu’un seul type de calcul possible sur une seule représentation possible des données.
L’affaire est tout autre pour le lecteur de MP3. D’abord, on ne manipule pas à proprement parler de signaux continus. Les morceaux de musique à jouer sont stockés sous une forme digitale dans la mémoire de l’appareil. « Stockés sous forme digitale » cela veut dire que l’on a représenté le morceau de musique par une suite de symboles abstrait pris dans un alphabet fini (en fait il n’y a que deux symboles, 0 et 1). Et là, c’est gagné ! Toute manipulation mécanique de ces symboles est un calcul. Et si ce calcul est effectué par une machine universelle, il est possible d’enchaîner d’autres calculs, de les faire évoluer et d’en faire d’autres… sans toucher à la structure physique du système. Ce que ne peut pas faire une machine analogique. Votre lecteur de MP3 peut alors embarquer, pour le même prix, un équaliseur, afficher les pochettes des disques (s’il était déjà doté d’un petit écran LCD) et aussi vous donner l’heure, ce que ne fera jamais un tourne-disque (sauf s’il est construit dès le départ pour embarquer un équaliseur et une horloge, mais alors il coûte plus cher).
Shawn Smith : Everett (2008), tilleul, peinture acrylique, branche. Shawn Smith, artiste américain, explore nos relations au monde numérique à travers la représentation d’animaux 3D construits à partir d’images pixellisées trouvées sur internet, afin de « comprendre comment chaque pixel joue un rôle dans l’identité d’un objet ».
On voit que la notion de calcul élaborée par Turing est très tolérante : la notion de calcul porte moins sur la nature de ce sur quoi on calcule que sur l’enchaînement des opérations, leurs itérations, leurs dépendances. Un ordinateur ne fait pas de différence entre calculer sur des entiers ou sur des morceaux de musique. Ce qui importe, c’est de manipuler des suites de symboles pris dans un ensemble fini.
Et c’est pourquoi, depuis les années 1950, les chercheurs et les ingénieurs s’efforcent de trouver une représentation digitale, un reflet numérique à tous les objets du monde et à développer des convertisseurs analogique → digital (capteurs) et digital → analogique (actuateurs) toujours plus performants pour relier et enchevêtrer le monde numérique au monde réel.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Jean-Louis Giavitto