Biathlon relais
Dans ce jeu, deux entraîneurs s’affrontent, ils doivent exploiter au mieux les capacités d’une même équipe d’athlètes. Les athlètes doivent d’abord effectuer un circuit en kayak puis une épreuve cycliste. L’équipe ne dispose pour cela que d’un unique kayak et d’un unique vélo, les athlètes doivent donc passer les uns après les autres. On lance le chronomètre quand le premier athlète s’installe dans le kayak pour ne l’arrêter que lorsque le dernier athlète descend du vélo. L’objectif est de terminer l’ensemble des épreuves le plus vite possible. On connaît les performances des athlètes dans chaque sport. Il faut, à partir de cette connaissance, décider quel est leur meilleur ordre de passage.
Qui sera le meilleur entraîneur ? Si vous jouez contre l’ordinateur, serez-vous meilleur que lui ?
Pour comparer les solutions, deux équipes aux performances individuelles égales sont montrées simultanément, l’une avec des dossards bleus, l’autre avec des dossards rouges.
Pour accéder à l’applet Java, autorisez les applets du domaine https://interstices.info. Si votre navigateur n’accepte plus le plug-in Java, mais que Java est installé sur votre ordinateur, vous pouvez télécharger le fichier JNLP, enregistrez-le avant de l’ouvrir avec Java Web Start.
Cette applet a été réalisée dans le cadre d’un projet étudiant de l’École Polytechnique de l’Université de Tours
par Chi Thanh Bui, encadré par Yannick Kergosien, Christophe Lenté et Jean-Charles Billaut.
Pour les personnages, merci à Andrew Scott du site DoppelMe.
Si l’applet ne s’affiche pas correctement, vérifiez que Java est installé et autorisez les applets du domaine https://interstices.info.
Évaluation d’une solution

La première difficulté consiste à calculer le temps nécessaire pour effectuer l’ensemble des épreuves. Pour cela, on peut s’aider d’un graphique. Prenons l’exemple d’une équipe composée de quatre athlètes dont les temps de parcours en kayak sont respectivement de 12, 15, 6 et 10 minutes et pour le vélo de 7, 12, 13 et 11 minutes. Supposons qu’on les fasse passer dans l’ordre 1, 2, 3 et 4.
Représentons le parcours d’un circuit par un rectangle de longueur proportionnelle au temps mis par l’athlète. Dans le diagramme ci-dessous, la première ligne correspond à l’épreuve de kayak et la seconde à celle de cyclisme. Les athlètes se succèdent dans l’ordre 1, 2, 3 et 4 sur chacune des épreuves. Une légende a été ajoutée sur chaque rectangle pour rappeler le numéro de l’athlète correspondant, ainsi que le temps mis pour effectuer le parcours.
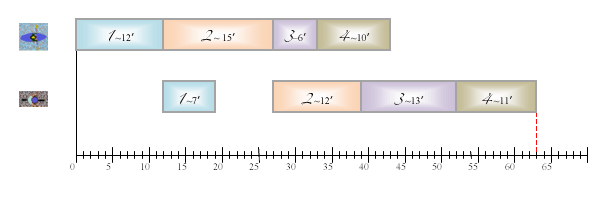
La première ligne est simple à construire, puisque dès qu’un athlète a fini l’épreuve de kayak, le suivant peut partir immédiatement. Il suffit donc d’accoler les rectangles les uns aux autres. La seconde ligne est un peu plus délicate à construire, car elle obéit à deux règles. La première dit qu’il n’y a qu’un seul vélo, les rectangles doivent donc se succéder dans l’ordre pré-établi de passage des athlètes. La seconde dit qu’un athlète doit avoir bouclé son circuit de kayak avant d’entamer celui de vélo. Un rectangle de la seconde ligne doit donc toujours se situer à la droite du rectangle qui lui est associé sur la première ligne. Cette seconde règle explique les espaces vides, les « trous » entre certains rectangles.
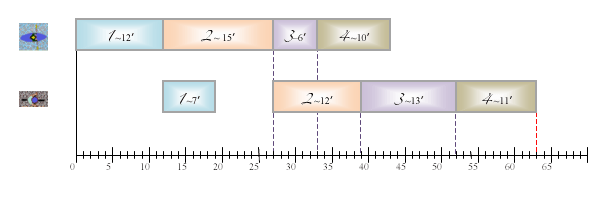
La lecture de ce diagramme, qui est connu sous le nom de diagramme de Gantt, nous renseigne sur l’impact de l’ordre qui a été choisi. Pour commencer, on constate que le dernier athlète termine son tour de vélo 63 minutes après que le premier a débuté l’épreuve de kayak. Mais on peut également obtenir des renseignements sur chaque athlète. Par exemple, le troisième athlète débute le kayak à la date 27 et boucle ce circuit à la date 33, puis il attend la date 39 pour monter sur le vélo et roule jusqu’à la date 42. On peut également voir qu’à la date 30, l’athlète 3 utilise le kayak pendant que l’athlète 2 utilise le vélo.
Choix du meilleur ordre
En observant le diagramme, on constate que le temps nécessaire pour faire passer tous les athlètes est donné par la fin de la seconde ligne. Cette ligne est composée de rectangles et de trous. Les longueurs des rectangles sont incompressibles car elles correspondent aux performances des athlètes, il faut donc s’arranger pour qu’il y ait le moins de trous possible. Ces trous correspondent en fait à des périodes où le vélo est inutilisé. Cette remarque permet de formuler une intuition de l’ordre optimal dans deux cas particuliers.
- Supposons que tous les athlètes passent moins de temps dans le kayak que sur le vélo, par exemple parce que le circuit de kayak est beaucoup plus court que celui de vélo. Dans le diagramme, il y a un trou qui est inévitable, c’est celui sous le premier rectangle. Pour que ce trou soit le plus petit possible, il faut placer en tête l’athlète le plus rapide en kayak, autrement dit, celui qui a le plus petit rectangle sur la ligne 1. Ensuite, le « rectangle kayak » de l’athlète en deuxième position se placera au-dessus du « rectangle vélo » de l’athlète en première position. Il faut s’arranger, dans la mesure du possible, pour que cela ne crée pas de trou sur la seconde ligne ou que le trou soit le plus petit possible. Pour cela, le mieux est de placer l’athlète le plus rapide sur le kayak, parmi ceux qui restent. Et ainsi de suite, on reproduit le même raisonnement pour chaque position. En conclusion, il faut classer les athlètes du plus rapide au moins rapide à l’épreuve de kayak ou encore par longueur de rectangle croissante sur la première ligne. On peut démontrer que cette règle d’ordonnancement est optimale sous l’hypothèse faite en début de paragraphe (que le temps de parcours en kayak soit inférieur au temps de parcours en vélo pour chaque athlète).
Cette méthode est celle utilisée par l’ordinateur au niveau Maître. - Considérons maintenant le cas inverse, c’est-à-dire que les athlètes passent systématiquement moins de temps sur le vélo que dans le kayak. Nous allons nous appuyer sur une propriété de symétrie du problème pour nous ramener à l’étude précédente. Considérons un ordre et son diagramme représentatif. Pour fixer les idées, supposons que les temps sur le kayak soient de 10, 14, 9 et 15 minutes et que les temps correspondants sur le vélo soient de 8, 12, 7 et 10 minutes.
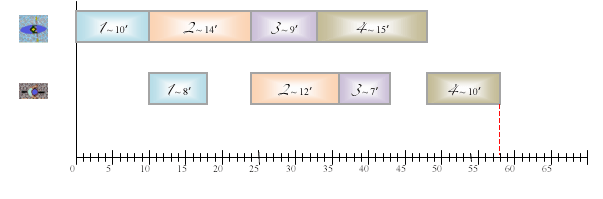
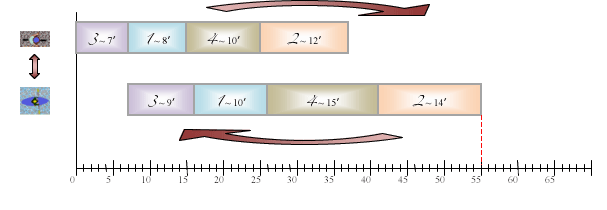
La durée totale associée à cet ordre est en fait la distance séparant le début du premier rectangle de la première ligne et la fin du dernier rectangle de la seconde ligne. Traçons maintenant une diagonale entre ces deux rectangles, prenons son milieu et effectuons une rotation de 180° autour de ce point.
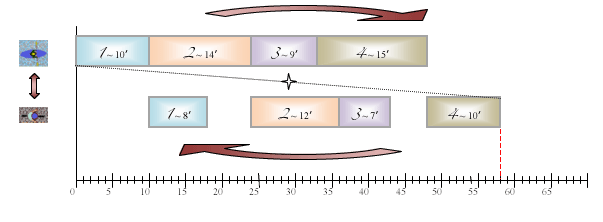
On obtient un diagramme inversé, dans lequel la première ligne correspond au vélo et la seconde au kayak, au détail près qu’il y a des trous sur la première ligne.
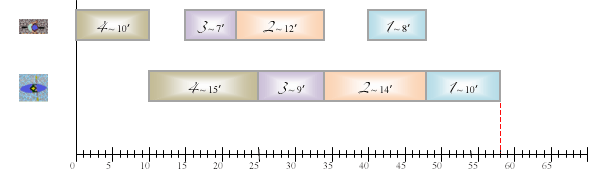
Qu’à cela ne tienne, tassons maintenant les rectangles vers la gauche, en prenant soin que chaque rectangle de la seconde ligne soit toujours à droite de celui auquel il est associé sur la première.
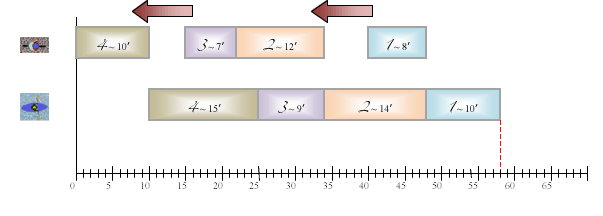
On obtient alors la représentation graphique d’une compétition où l’épreuve cycliste se déroulerait avant l’épreuve de kayak.
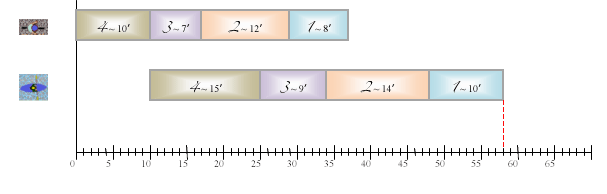
On sait alors, d’après l’étude précédente, qu’il faut classer les athlètes par longueur de rectangle croissante sur la première ligne.
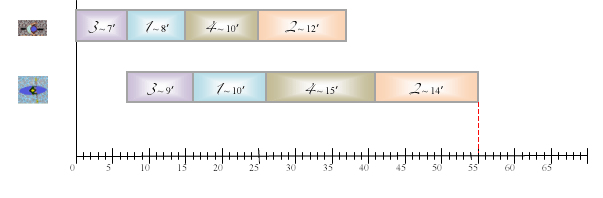
Il suffit enfin de refaire une rotation de 180° pour revenir au problème initial.
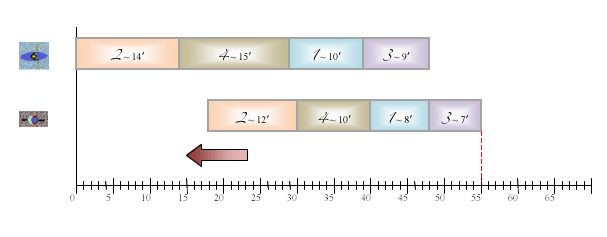
Cela signifie qu’il fallait classer les athlètes par longueur de rectangle décroissante sur la seconde ligne, soit encore du moins rapide au plus rapide sur l’épreuve cycliste.

Cette méthode est celle utilisée par l’ordinateur au niveau Débutant.
- Et dans le cas général ? L’étude du problème montre qu’il faut combiner les deux cas précédents. On commence par séparer les athlètes en deux groupes : on place en premier ceux qui passent moins de temps dans le kayak que sur le vélo, classés du plus rapide au moins rapide à l’épreuve de kayak, suivis de ceux qui passent moins de temps sur le vélo, classés du moins rapide au plus rapide à l’épreuve de cyclisme.
Cette méthode, toujours optimale, est celle utilisée par l’ordinateur au niveau Expert.
Si on reprend le premier exemple, cela veut dire qu’on fait d’abord passer les athlètes 3 et 4 dans cet ordre, puis les athlètes 1 et 2 dans l’ordre 2 – 1. L’ordre retenu est donc : 3, 4, 2 et 1 pour une durée totale de 50 minutes. Si on avait classé les athlètes par temps croissants sur le kayak (ordre 3, 4, 1 et 2), on aurait obtenu une durée totale de 55 minutes et si on les avait classés par durées décroissantes sur le vélo (ordre 3, 2, 4 et 1), on aurait obtenu une durée totale de 51 minutes.
À quoi ça sert ?
Imaginez un petit atelier qui fabrique des étagères « à monter soi-même ». Le processus de fabrication s’effectue en deux étapes, une première machine découpe des planches à la taille requise et une seconde machine se charge de percer les trous nécessaires à l’assemblage. Suivant le modèle de l’étagère, la découpe ou le perçage prennent plus ou moins de temps. Le chef d’atelier a un carnet de commandes et son objectif est de terminer le travail le plus vite possible. Dans ce problème d’ordonnancement d’atelier, les machines correspondent au kayak et au vélo et les commandes d’étagères jouent le rôle des athlètes. Ce type d’atelier est appelé flowshop (ou atelier en flux) à deux machines. Il a été étudié pour la première fois par Johnson en 1954, qui à cette occasion a proposé l’algorithme de classement décrit dans le paragraphe précédent.
En général, les ateliers sont bien plus complexes que ce petit exemple. Si on ajoute ne serait-ce qu’une troisième machine, le problème devient NP-difficile, ce qui explique que les problèmes d’ordonnancement d’ateliers soient encore l’objet de nombreuses études théoriques.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Christophe Lenté
Maître de conférences au Laboratoire d'informatique et à l'École Polytechnique de l'Université de Tours.

Yannick Kergosien
Maître de conférences à l'Université de Tours (Laboratoire d'informatique) et à l'École Polytechnique de l'Université de Tours.

Jean-Charles Billaut
Professeur à l'Université de Tours, directeur du Laboratoire d'informatique et enseignant à l'École Polytechnique de l'Université de Tours, ancien président de l'association ROADEF.