Démixer la musique

La séparation de sources consiste à récupérer plusieurs signaux à partir de l’observation de leur mélange. Dans le domaine du son, cette problématique est souvent introduite en évoquant l’effet cocktail party. Lors d’une réception, de nombreuses voix simultanées parviennent à mes oreilles. Pourtant, je suis capable si je le souhaite de ne porter mon attention que sur l’une d’entre elles. Ce faisant, j’ai réduit l’influence des autres voix dans la compréhension de ce qui m’intéresse. Pour cela, mon cerveau a séparé certains sons des autres.

De la même manière, en écoutant une chanson, je peux me concentrer sur l’un des instruments, en l’isolant ainsi mentalement des autres. Cette capacité, si elle pouvait être imitée par une machine, permettrait l’extraction ou la suppression à l’envi de n’importe quel son d’un enregistrement audio. Par exemple, nous pourrions enlever automatiquement la voix d’un morceau pour en faire une version karaoké, ou bien au contraire l’isoler pour l’utiliser dans un nouveau morceau. En focalisant sur la voix dans un environnement bruité, nous pourrions aussi améliorer le fonctionnement des aides auditives ou la compréhension automatique des mots prononcés. Il est donc légitime qu’une large communauté de chercheurs en traitement du signal audio se soit penchée sur le problème.

Masquage temps-fréquence

Considérons le cas d’un morceau de musique stéréo. Il est composé d’un canal gauche et d’un canal droit. Nous appellerons ce signal le mélange, parce qu’il est la superposition des différents sons que nous cherchons à séparer, appelés sources. Le son produit par chaque instrument s’entend à la fois à gauche et à droite, en même temps que les autres instruments. En effet, un ingénieur du son a travaillé pour fabriquer un mélange qui soit agréable à écouter, dans lequel tous les instruments s’entendent. Ici, notre objectif est de réaliser l’opération inverse, il s’agit en quelque sorte de démixer la musique, dans le but d’isoler les sons des différents instruments.

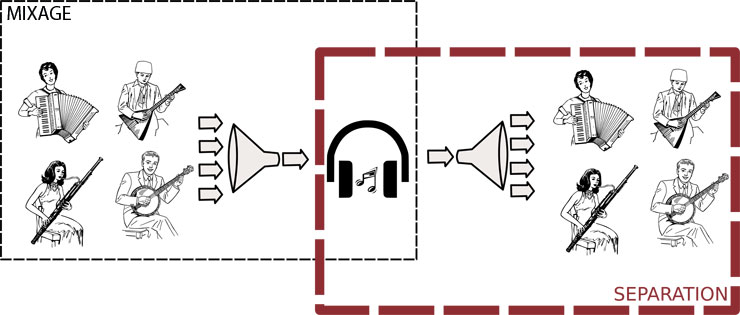
La séparation est habituellement comprise comme une opération de filtrage, ce qui signifie que pour récupérer le son d’un seul instrument, on va supprimer du mélange tout ce qui ne lui correspond pas.

Un filtre peut être compris comme un égaliseur, semblable à celui des autoradios, qui va atténuer ou amplifier certaines fréquences. La plage de fréquences des CD musicaux est de 0 à 22.05 kHz. Si notre objectif est par exemple d’extraire la basse, une solution pourrait être de simplement supprimer tous les aigus du mélange. Cette approche peut marcher à la condition que, dans toutes les fréquences que nous gardons, seul le son cible soit présent. En pratique, il est nécessaire de considérer environ un millier de bandes de fréquences, de manière à avoir une précision suffisante pour que dans chacune il n’y ait qu’un seul instrument présent à la fois. Ensuite, l’essentiel de notre travail consiste à choisir quelles bandes il nous faut atténuer ou conserver, dans le but d’isoler un instrument donné. Pour compliquer les choses, nous sommes obligés de changer ce choix très régulièrement, parce que le morceau change constamment. La séparation de sources audio consiste ainsi à définir quelles fréquences garder ou supprimer, et à faire ce choix pour environ 1000 bandes de fréquences, toutes les 20 ms.

D’un point de vue technique, l’opération de séparation requiert une représentation temps-fréquence du son, qui est souvent la Transformée de Fourier à Court Terme (TFCT). Son principe est de découper le son en petits bouts appelés trames, qui correspondent au son pendant de petits intervalles de temps. Chaque trame est alors décomposée en une somme de sons purs, sinusoïdaux, par une Transformée de Fourier. N’importe quel son peut être représenté de cette manière. Dans la suite de cet article, nous appellerons x(f, t) la TFCT de notre morceau de musique. Il s’agit de la fonction qui donne la portion du son qui vibre à chaque fréquence f, à chaque temps t. Elle contient une information de puissance et de phase : le module et l’argument du nombre complexe x(f,t). Si on regarde sa puissance⎮x (f, t)⎮², appelée spectrogramme, on obtient une image qui nous informe sur l’évolution au cours du temps du contenu fréquentiel d’un enregistrement sonore. Par exemple, voici le spectrogramme d’un enregistrement de voix chantée.

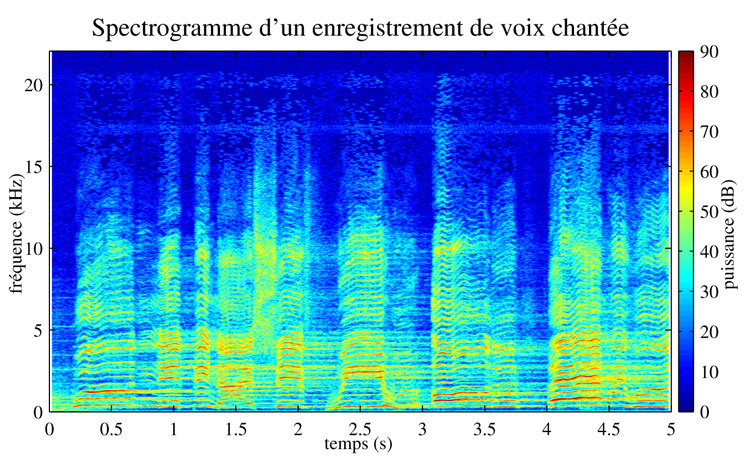
Dans une telle représentation, le rouge nous indique que de l’énergie est présente dans le signal. Cette visualisation permet à l’expert d’analyser les sons. Par exemple, dans le cas de la voix, un phonéticien professionnel serait capable de transcrire le son pour deviner quelles sont les paroles du morceau, uniquement en regardant le spectrogramme ! On appelle « point temps-fréquence » chaque pixel d’un tel spectrogramme.

Maintenant, considérons que notre morceau est la somme de J différents sons à séparer. Pour le cas d’un quatuor, nous avons par exemple J = 4. Tout comme les ondes qui se propagent à la surface de l’eau, les formes d’ondes sonores s’ajoutent. La Transformée de Fourier du morceau est alors simplement égale à la somme des Transformées de Fourier des sources :
x(f, t) = s₁ (f, t) + s₂ (f, t) + s₃ (f, t) + s₄ (f, t)

Dans cette équation, le nombre complexe s₁ (f, t) est la TFCT de la source 1, mettons l’accordéon, s₂ (f, t) celle de la source 2, etc.

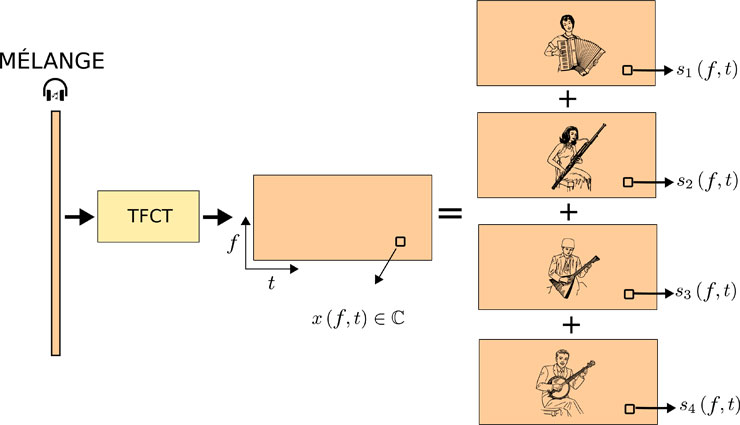
Notre problème est donc de récupérer les TFCT s_j des sources à partir de celle du mélange x.  Comme nous l’avons suggéré plus haut, cela peut être fait en supprimant ou en conservant certaines fréquences au cours du temps.

À un instant t et pour une fréquence f donnés, le signal que nous observons est noté x (f, t). Appliquer une égalisation au signal à cette fréquence f et ce temps t peut être fait très simplement en multipliant x (f,t) par une valeur entre 0 et 1, appelée « gain » : si on choisit 0, on atténue totalement cette bande de fréquence, on la garde au contraire intacte si on choisit 1. Ce gain utilisé pour séparer une source dépend à la fois du temps et de la fréquence, nous l’appelons  « masque temps-fréquence » et le notons w₁ (f, t) : c’est l’égalisation à appliquer à la TFCT du mélange pour récupérer une bonne estimée de la source 1. On note cette estimée \(\hat{s}_{1}\left(f,t\right)\) (prononcer « s₁ chapeau »).

Il est possible de donner directement une valeur à ce gain w₁ (f, t) utilisé pour extraire la source 1. Habituellement, on choisit alors une valeur égale à 0 ou à 1, qui revient soit à éliminer ce point, soit à le conserver, pour estimer la source. On dit dans ce cas que le masque temps-fréquence est binaire.

Il est aussi possible de choisir n’importe quelle valeur entre 0 et 1, afin d’obtenir des sons séparés plus agréables à entendre. Dans ce cas, on exploite souvent la notion de spectrogramme de puissance que nous avons vue plus haut. Supposons pour l’heure que nous connaissions les puissances de toutes les sources à chaque fréquence f et à chaque instant t, notées v_j (f, t) ≥ 0. Pour extraire la source 1, on utilise alors souvent un masque qui porte le nom de filtrage de Wiener, en l’honneur de Norbert Wiener (1894-1964) qui l’a proposé pour la première fois. Il revient à choisir pour masque d’une source la proportion de sa puissance par rapport à la somme des puissances de toutes les sources v₁ + v₂ + … + v_J. Cela s’écrit par l’équation suivante :

\[
w_{1}\left(f,t\right)=\frac{v_{1}\left(f,t\right)}{\sum_{j=1}^{J}v_{j}\left(f,t\right)}.
\]

Un tel choix garantit que si v₁ est très grand devant les autres v_j , le masque aura une valeur proche de 1. Sinon, il aura une valeur proche de 0. Si les puissances sont connues, le son séparé obtenu de cette manière sera très bon. Cependant, les spectrogrammes de puissance des sources sont en pratique inconnus, et nous avons besoin de les « deviner » à partir du mélange.

Modéliser la musique

Fabriquer un masque temps-fréquence est une tâche difficile. Le nombre de paramètres à régler est en effet très grand. Dans notre exemple, il est pour chaque source de 1000 bandes de fréquences multipliées par le nombre de trames, habituellement des dizaines de milliers. Bien qu’il soit en théorie possible de le faire à la main, cela nécessiterait un travail laborieux de la part de l’utilisateur, de l’ordre de plusieurs heures pour quelques secondes de son. Plusieurs idées ont ainsi été proposées pour calculer les masques temps-fréquence automatiquement.

Une première méthode se nomme DUET, pour Degenerate Unmixing Estimation Technique. Elle repose sur l’idée que dans un morceau stéréo, les différents instruments sont souvent placés à différents endroits de l’espace stéréo, c’est-à-dire entre la gauche et la droite. Un utilisateur peut facilement nous donner une telle information, comme « la guitare est à droite » ou « la voix est au centre ». Dans ces conditions, pour une trame et une fréquence donnée, nous pouvons regarder si le son est plus fort à gauche, à droite, ou à peu près égal. Ce critère nous permet de décider à quelle source nous devons associer ce point temps-fréquence. Cette première méthode est dite spatiale, parce qu’elle exploite surtout la position des sources dans l’espace stéréo. Elle fonctionne très bien pour les morceaux de musique qui exploitent pleinement la stéréo, et dont le nombre d’instruments n’est pas trop grand. Ce sera par exemple le cas pour certains enregistrements des années 70, tels ceux des Beatles. DUET fonctionnera mal lorsqu’il y a beaucoup d’instruments, ou bien lorsque leur position dans le plan stéréo n’est pas très précise, comme cela arrive lorsqu’il y a de la réverbération. Des améliorations ont été proposées depuis, où on ne suppose plus qu’un instrument est à une position précise, mais plutôt qu’il présente une certaine corrélation entre la gauche et la droite. Dans le cas où le mélange est très compliqué, notamment en raison de la multiplicité des sources, cela permet de lever les ambiguïtés et d’ainsi obtenir de bien meilleurs résultats.

Le problème d’une telle séparation purement spatiale est qu’elle ne peut pas fonctionner pour séparer des sources qui ont la même position dans le plan stéréo. Par exemple, il est très courant dans la musique populaire de placer la basse, la grosse caisse et la voix au centre. Il est alors impossible de séparer ces sons en utilisant uniquement des critères spatiaux et il devient nécessaire de prendre aussi en compte la nature de ces signaux par des critères spectraux.

Un exemple classique est la séparation harmonique-percussive. Dans un morceau de musique, il s’agit d’isoler les sons impulsifs de la batterie des autres sons du morceau, qui sont dits harmoniques. Pour comprendre ce qui distingue ces sons, il suffit d’en regarder le spectrogramme.

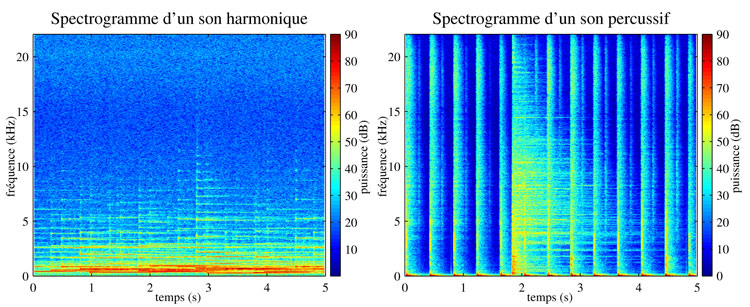
Les sons harmoniques ont un contenu spectral qui évolue peu au cours du temps : on voit des lignes horizontales, qui correspondent aux différentes fréquences qui le composent. Ces fréquences produisent une nette sensation de hauteur lorsque nous écoutons le son. Cette hauteur est ce qu’un musicien appellera une note, et placera sur une partition. Au contraire, les sons impulsifs de la batterie sont très courts, et on voit qu’ils activent toutes les fréquences à la fois. Visuellement, leur spectrogramme présentera de nombreuses lignes verticales. Ainsi, la méthode proposée par D. Fitzgerald  consiste à identifier toutes les lignes horizontales du spectrogramme du mélange comme correspondant à la source harmonique, tandis que les lignes verticales seront rassemblées dans la source percussive. Cette technique très efficace permet d’identifier simplement les spectrogrammes de ces deux sources et de les séparer grâce à un filtre de Wiener. De façon similaire, dans le cas de la voix parlée ou chantée, des techniques plus récentes permettent d’apprendre la forme du spectrogramme des différents sons de la voix et de l’exploiter pour la séparation.

Deux exemples à écouter

Voici deux exemples à écouter de séparation de la voix et de l’accompagnement instrumental. Le système fonctionne de la même manière que l’exemple harmonique/percussif donné ci-dessus, mais discrimine entre les sons répétitifs de l’accompagnement musical et les sons non-répétitifs  de la voix.

Conclusion

Démixer la musique en séparant les sources sonores requiert des systèmes de filtrage sophistiqués qui sont rendus possibles grâce à des connaissances dans le domaine des mathématiques appliquées, de l’informatique et de l’acoustique. Plus généralement, la séparation de sources est un problème difficile qui a des applications dans de nombreux autres domaines, les télécommunications, l’imagerie hyperspectrale ou le traitement des signaux biomédicaux. Dans la plupart des cas, les techniques mises en œuvre compensent une indétermination du problème, qui comprend plus d’inconnues que d’équations, par la prise en compte de connaissances sur la nature des signaux à séparer. Si nous avons vu certains exemples simples de modèles spécifiques à la musique, d’autres champs d’application exploitent des propriétés spécifiques à leur domaine. Ainsi, sans en connaître exactement la forme, on peut savoir par exemple qu’un des signaux à séparer est périodique, ou qu’un autre est lisse, tandis qu’un troisième est un bruit imprévisible.