La simulation par ordinateur change-t-elle les sciences ?

« En cet Empire, l’art de la cartographie fut poussé à une telle perfection que la carte d’une seule province occupait toute une ville et la carte de l’Empire toute une province. Avec le temps, ces cartes démesurées cessèrent de donner satisfaction et les collèges de cartographes levèrent une carte de l’Empire, qui avait le format de l’Empire et qui coïncidait avec lui, point par point. Moins passionnées pour l’étude de la cartographie, les générations suivantes réfléchirent que cette carte dilatée était inutile et, non sans impiété, elles l’abandonnèrent à l’inclémence du soleil et des hivers. »
Suarez Miranda, Viajes de Varones Prudentes (1658), imaginé par J.-L. Borges, Histoire universelle de l’infamie/Histoire de l’éternité, Union générale d’éditions, collection 10/18, Paris.

L’ ordinateur a changé les pratiques des mathématiciens, en les aidant à énoncer des hypothèses et des résultats, en produisant la démonstration de théorèmes qu’aucun humain ne peut mener, en validant des preuves complexes ou douteuses. Ce n’est peut-être pas étonnant puisque, comme le mathématicien, l’ordinateur manipule des nombres, des symboles et des règles logiques. En revanche, dans les sciences de la nature, son usage ne va pas de soi.

Quels rapports entretiennent avec la réalité la modélisation informatique et la mise en œuvre dynamique des modèles – la simulation ? Que représentent la modélisation et la simulation dans la pratique de la recherche scientifique : un outil de description formelle, destiné à se substituer à l’outil mathématique ? Une technique expérimentale simplifiant ou dispensant de l’observation du monde réel ? Une méthode d’exploration d’hypothèses concurrentes ? Peut-être sont-elles tout cela à la fois, c’est-à-dire une forme nouvelle de l’activité scientifique, sans équivalent dans le passé, que les chercheurs de toutes les disciplines déclinent à leur manière, jour après jour. Donner des éléments concrets de réflexion sur ces questions et informer sur ce qui apparaît comme un bouleversement profond dans la pratique scientifique, c’est l’objectif du dossier de la revue Pour la science La modélisation informatique, exploration du réel, élaboré avec Interstices, dont ce document trace les lignes directrices et dont les différentes contributions seront mises en ligne progressivement sur ce site.

Tout modèle est faux, et c’est très bien !

Commençons par nous débarrasser d’une idée reçue : la modélisation n’est pas destinée à reproduire exactement la réalité. Seul un modèle identique au système pourrait être considéré comme une représentation exacte de ce dernier. Or, tout comme la légendaire carte à l’échelle 1/1 de Borges, un tel modèle ne peut être construit, et, tout comme cette carte, il ne présenterait aucun intérêt. En effet, l’élaboration d’un modèle est motivée par un ensemble de questions auxquelles ce modèle doit contribuer à répondre. Quel avantage à disposer d’un modèle de même complexité que son objet ?

La modélisation procède d’une longue suite de décisions : quels sont les sous-systèmes et quelle hiérarchie les organise ? Quelles sont les variables à prendre en compte ? Quelle formulation de leurs interactions retenir ? Tous ces choix sont orientés par les questions initiales. Ainsi, de même qu’il existe une multitude de cartes pour un même territoire – routières, géologiques, climatiques… à des échelles différentes selon les besoins –, un même système sera modélisé fort différemment selon les objectifs de ses concepteurs. Plus qu’un portrait, un modèle est une caricature, qui ne retient que les traits pertinents compte tenu des attentes formulées.

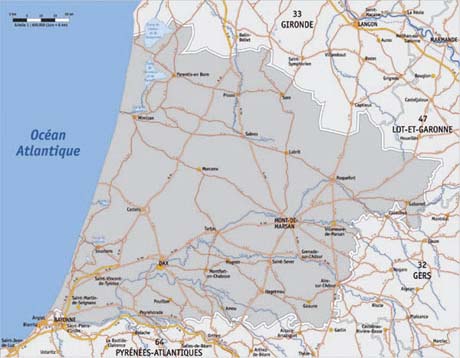
Une carte qui représenterait un territoire (ici les Landes) à l’identique et à la même échelle ne servirait à rien. Au contraire, une carte ne rassemble que les informations jugées utiles pour une utilisation déterminée. De même un modèle représente un aspect particulier d’un système étudié, pour permettre de répondre à un ensemble de questions précises. Infographies : Pour la Science

Ces choix sont aussi déterminés par le niveau de connaissance que les modélisateurs ont de leur système. Ce dernier est imparfaitement connu, c’est pourquoi on cherche à le modéliser. On introduit ses nombreuses interactions une à une dans le modèle, puis la simulation en fait la synthèse et révèle les comportements qui en résultent. De ce point de vue, les comportements inattendus sont plus instructifs que ceux qui reproduisent ce que l’on sait déjà du système. Ils mettent en évidence les incompréhensions et les formulations inadéquates, et forcent à revenir sur la modélisation, à chercher de nouvelles interactions, voire à planifier de nouvelles observations. C’est en suivant ce processus itératif que les modélisateurs affinent leur compréhension du système. Le premier mérite d’un modèle, c’est d’avoir été construit.

Le processus de modélisation n’est jamais abouti, et l’idée d’un modèle-produit cédé à des utilisateurs-clients est quelque peu dangereuse. Peut-on utiliser un modèle de façon pertinente quand on n’a pas participé à son élaboration ? La question est cruciale pour les modèles destinés à la prédiction. La confrontation du modèle à la perception du système qu’ont ses « utilisateurs » doit se poursuivre, et les révisions nécessaires doivent être apportées en conséquence. En outre, aucune « prédiction » issue d’un modèle ne saurait être utilisée telle quelle. Ne valant que ce que valent les hypothèses constitutives du modèle, les résultats d’une simulation ne produisent que des scenarios d’évolution. C’est par la production et l’examen de nombreuses simulations sous des hypothèses différentes que les utilisateurs d’un modèle formulent progressivement des futurs possibles, et peuvent recommander des décisions.

La question est, non pas de savoir si un modèle est correct ou non, mais d’apprécier son apport dans un processus de compréhension progressive du système et de ses comportements, motivé par un ensemble de questions initialement explicitées. Un bon modèle est un modèle utile.

Des usages multiples

Qu’est-ce donc que ce modèle utile, cette « carte » adaptée au scientifique sur le point d’explorer une contrée inconnue de sa discipline ? Si l’on s’en tient aux schémas traditionnels du fonctionnement des sciences, on est tenté de ramener l’usage de l’ordinateur à quelques applications prédéfinies qui fixeraient sa bonne exploitation scientifique. L’ordinateur calcule, de même que, de tout temps, l’astronome a calculé. Un modèle informatique n’est qu’un type particulier de modèle mathématique. Une simulation n’est qu’un calcul compliqué, déroulant les états successifs du modèle, comme le mathématicien fait depuis longtemps en résolvant des systèmes d’équations, etc.

Un modèle est-il une nouvelle caverne de Platon ? Représente-t-il une simple projection de la réalité ? Pour pouvoir en tirer des enseignements sur le système réel qu’il représente, l’utilisateur doit être conscient des limites de son modèle.
(Gravure : La caverne de Platon , XVI^e siècle, conservée à la Bibliothèque Nationale, Paris, France / Archives Charmet.)
Photo © The Bridgeman Art Library

Cette attitude conservatrice ne tient pas compte de l’évidente nouveauté de la modélisation informatique. Elle ne semble pas défendable pour qui examine la pratique réelle de chaque discipline. En effet, chacune invente pour son propre compte de nouvelles manières de mettre l’ordinateur au service de ses buts. Il s’ensuit une explosion de configurations théoriques imprévues, où la modélisation et la simulation tantôt aident à formuler les théories – voire en constituent le cœur –, réalisent des expériences aussi cruciales que les expériences traditionnelles, produisent des « observations » déterminantes, ou sont elles-mêmes des objectifs qu’on cherche à atteindre sans copier le détail précis des objets, structures, espaces ou entités complexes qu’on modélise et simule. Ce foisonnement ne manquera pas de surprendre, tant il montre que les modèles informatiques donnent aux scientifiques bien plus qu’ils n’en attendaient.

Pour tenter d’ordonner la multitude, on peut organiser les exemples de modèles informatiques en trois grandes parties : la première concerne les sciences fondamentales, la deuxième la prédiction ainsi que l’aide à la décision, et la dernière, la technologie.

L’élaboration des connaissances

La première partie est consacrée aux plus troublants usages et pratiques de la modélisation et de la simulation : ceux qui s’insinuent au cœur même de la recherche fondamentale, ceux qui aident à comprendre des phénomènes et donc à formuler les théories, découvrir les faits, voir les objets, que sans eux on ne formulerait pas, on ne découvrirait pas, on ne verrait pas.

Qui aurait imaginé qu’un calcul conduise à identifier une nouvelle particule comme le révèlent les recherches de D. Weingarten (voir Quarks et simulation numérique), ou que la mise au point d’ordinateurs spécialisés se substitue à la construction d’accélérateurs et détermine la masse de particules élémentaires ? Cette physique théorique expérimentale signifie-t-elle que toute expérience devient inutile ? Ce serait aller trop loin et Jean Zinn-Justin (CEA, Saclay) nous met en garde : « La simulation numérique ne peut intervenir que dans des domaines où la théorie a déjà des bases suffisamment solides ; elle ne peut rien tant que les modèles physiques ne sont pas encore connus. »

Pourtant, dans l’étude des phénomènes astronomiques, la simulation produit une étonnante science qui « observe » grâce aux calculs de l’ordinateur. À propos de l’évolution des galaxies, Françoise Combes affirme : « Grâce à la simulation numérique, les astronomes ont été les témoins de phénomènes dynamiques que les calculs analytiques ne pouvaient pas traiter, ni même soupçonner ». L’ordinateur se substitue ici au mathématicien qui ne peut résoudre les trop difficiles équations que la théorie engendre. En exécutant ses programmes et en montrant les solutions qu’il calcule, il rend disponibles à l’astronome de nouveaux faits d’observation. La distinction entre l’activité théorique – raisonnements, calculs – et les observations semble vaciller. La simulation par ordinateur révèle ici une catégorie de vérités intermédiaires : ni tout à fait analytiques, ni tout à fait d’observation.

Concernant la turbulence dans les plasmas, Laurent Villard évoque, lui aussi, la possibilité que confère la simulation numérique « d’observer des phénomènes physiques avec un niveau de détail bien supérieur à ce qui peut être mesuré expérimentalement » : le modèle mis dans l’ordinateur est ce qui permet de voir le monde et, dans un tel cas, il est plus précis que les instruments d’observation classiques ! La philosophie des sciences a depuis longtemps attiré l’attention sur l’impossibilité de produire des faits purs indépendamment des théories ; ici il semble que les théories mises dans l’ordinateur par le biais des modèles et laissées à leur logique calculatoire massive produisent des quasi faits non déductibles sans lui de la théorie, et parfois non observables directement dans la nature (cas des plasmas). L’ordinateur n’est pas un auxiliaire facultatif de la théorie et de l’observation : il permet la formulation des théories et il produit l’observation.

Notons aussi que les simulations informatiques ont prouvé leurs capacités prédictives. Citons deux exemples : les simulations à autogravité firent apparaître des barres en travers des disques galactiques dont, après coup, on constate que 80 pour cent des galaxies sont pourvues lorsqu’on les observe en proche infrarouge. Dans un tout autre domaine, les expérimentations virtuelles sur les araignées sociales permirent la formulation de l’hypothèse que la taille d’une toile dépend du niveau de satiété de l’animal, laquelle influence la force d’attraction de la toile, hypothèse validée ultérieurement par l’observation (voir La stratégie de l’araignée, par V. Chevrier).

Entre théories et réalités…

Le fonctionnement normal d’une science serait, non plus un va-et-vient entre la théorie et le monde réel, mais un jeu plus complexe et plus varié à trois, entre la théorie, les modèles placés dans l’ordinateur et le monde réel.

Un modèle est-il un oracle, à l’image de l’oracle de Delphes, ou un sphinx aux énigmes insolubles ? Peut-il aider à prévoir l’avenir pour prendre les bonnes décisions ? Une confrontation permanente entre le modèle et la réalité permet d’affiner les prévisions et d’évaluer les incertitudes.
(Tableau Oedipe explique l’énigme du sphinx, peint par Jean-Auguste-Dominique Ingres (1780-1867), conservé au Musée du Louvre.)
Photo © RMN / René-Gabriel Ojéda

La simulation serait devenue un outil central, au même titre que les mathématiques, qu’elle utilise souvent pour projeter dans la machine des hypothèses, mais qu’elle abandonne (partiellement) préférant chercher les solutions à coup de gigaflops plutôt qu’à coup de raisonnements et de théorèmes. Ce relatif recul des mathématiques – résultant de ce qu’elles permettent de formuler plus de problèmes qu’elles ne savent en résoudre – n’exclut pas que d’autres mathématiques numériques, combinatoires et algorithmiques prennent la relève. Celles-ci posent des questions fondamentales et conduisent au développement de nouveaux domaines comme la zoologie des automates cellulaires étudiés notamment par M. Delorme et J. Mazoyer, dont la profondeur des interrogations ne manquera pas d’intéresser les philosophes.

Ajoutons à cela que l’outil – le modèle comme objet mathématique –  lui-même demande à être compris, ce qui réserve parfois des surprises comme Raoul Robert nous en donne un bel exemple (voir L’effet papillon n’existe plus !). En effet, selon que l’on prend en compte un petit ou un grand nombre de degrés de liberté, le système évolue très différemment : soit il exhibe la fameuse sensibilité aux conditions initiales (qui conduit à l’effet papillon), soit il ne la montre pas. En définitive, il est difficile de ne pas confondre les propriétés du modèle et celles du système réel, dans ce contexte nouveau où artefacts numériques, approximations, projections, extractions et visualisations des données sont autant de sources d’erreurs et d’illusions.

La simulation fournit de la compréhension, elle permet de formuler les théories, de les tester et, parfois, elle conduit même à la constitution de domaines inconcevables sans elle, fonctionnant selon une logique centrée sur l’ordinateur (voir Modéliser le vivant : créer des plantes virtuelles pour comprendre, simuler, tester, de Ch. Godin, H. Sinoquet, É. Costes et J. Traas).

La simulation pour regarder vers le futur

À cette première partie où la modélisation et la simulation aident à la compréhension succède une seconde partie, moins dérangeante, car plus facile à ranger dans nos catégories anciennes : la simulation pour la prédiction et l’anticipation et donc l’aide à la décision. Notons que certains exemples de la première partie auraient pu aussi bien se trouver dans la seconde et réciproquement : la classification que nous proposons est délicate.

L’idée consiste ici à réaliser un micromonde numérique, le plus semblable possible au monde réel ou à sa partie pertinente, et à le faire « tourner » grâce à l’ordinateur, pour prévoir le temps de demain ou savoir comment se comporteront les marchés l’année prochaine si tel événement se produit. Le modèle dans ce cas résulte d’une théorie à peu près arrêtée et de choix de représentations (plus ou moins précis, omettant volontairement telle ou telle caractéristique jugée secondaire) qu’on fait fonctionner pour voir en avant dans le temps. On simplifie délibérément en tentant d’identifier ce que la simplification masque ou déforme.

On discute par conséquent le niveau de précision du modèle, et on espère qu’il soit « suffisamment proche de la réalité pour pouvoir simuler un grand nombre de caractéristiques réelles », comme le disent A. Chaigne, G.  Derveaux, P. Joly à propos de simulations de la guitare acoustique (voir Modélisation numérique de la guitare acoustique et Comprendre la guitare acoustique). Cependant, ainsi que le rappelle M. Thiriet (voir Marc Thiriet : il simule les fluides de notre corps et L’air et le sang : les écoulements in vivo), il faut adopter le précepte de Guillaume d’Ockham, c’est-à-dire ne pas multiplier inutilement les éléments et paramètres du modèle, lequel doit rester le plus simple possible. Comme le précisent M. Ha Duong et P. Matarasso qui étudient comment intégrer l’économie, l’énergie et le climat, cela entraîne la nécessité d’évaluer et de cerner les limites du modèle, ce qui oblige à envisager plusieurs « niveaux d’incertitude dans les résultats du modèle », notamment dans les modèles intégrés associant plusieurs disciplines.

Dans ce processus, les techniques de paramétrisation et de validation des modèles deviennent complexes. Elles associent un travail de confrontation des données avec des résultats partiels et locaux et demandent de nombreux ajustements (modifiant parfois profondément le modèle lui-même). Cette situation est illustrée par l’exemple délicat et pourtant si important des travaux sur le changement climatique (voir Comment estimer le changement climatique ?, par Serge Planton).

Ces modèles utilisés pour prédire et anticiper l’avenir servent aussi à évaluer les décisions à prendre. O. Brandouy et Ph. Mathieu, à propos de la finance des marchés (voir Marchés financiers artificiels), évoquent une expérimentation de la taxe Tobin non testable dans la réalité. On le voit, la simulation est devenue un outil fondamental pour faire parler les théories et tenter d’en tirer des prédictions de comportement futur.

Copier sans chercher à être fidèle

Des modèles-théories de la première partie – où l’ordinateur formule et explore les hypothèses formelles et produit des faits – aux modèles-prédictifs de la seconde – où l’ordinateur tire les conséquences numériques d’une série d’hypothèses mises en calcul dans ses mémoires –, l’ambition de représentation du réel s’est légèrement relâchée. Dans la troisième partie, l’objectif de modélisation ne portera plus que sur quelques aspects limités, les modèles étant ici utilisés non plus pour représenter ou prédire, mais pour créer des objets ressemblant approximativement – voire superficiellement – à d’autres objets du réel.

Il s’agit par exemple de copier des parties du corps humain pour réaliser des simulateurs de chirurgie (voir Simulation de chirurgie hépatique, par H. Delingette et N. Ayache) ou de s’inspirer du déplacement humain pour stimuler des membres paralysés (voir Recherche en marche et Restaurer la marche grâce à une puce de David Guiraud), ou encore d’imiter certains aspects de la vision humaine ou animale pour qu’un robot voie (voir La grenouille et le robot, par Th. Vieville), ou enfin d’analyser la géométrie des formes en trois dimensions pour minimiser le coût en mémoire d’ordinateur (voir Compression de maillages, par P. Alliez).

Le chercheur explore la nature pour y trouver des solutions algorithmiques et techniques qu’il ne sait imaginer seul. L’ingéniosité nécessaire, l’importance de ces réalisations, la finitude des ressources informatiques que l’on doit économiser, tout cela stimule la créativité et ouvre de nouveaux champs de la modélisation et de la simulation. Celles-ci voient décidément leur empire couvrir tous les aspects de la recherche scientifique et technique, ce qui met la recherche en informatique au centre d’un nombre toujours plus grand de domaines scientifiques.