La soirée
Il est très inhabituel de recevoir un télégramme de nos jours, dit Ecco en ouvrant l’enveloppe. Et sa teneur est encore plus inhabituelle. Qu’en pensez-vous, professeur ?
Voici le télégramme :
Dr Ecco ai besoin votre aide pour énigme stop pense issue de la mythologie grecque stop vous rendrai visite demain après-midi.
« Vous êtes un amateur éclairé de mythologie grecque, n’est-ce pas ? dis-je en montrant une rangée de livres.
– Un amateur, c’est le mot. Mais, à en juger par le ton de ce télégramme, j’en sais peut-être plus long que notre client, qui doit d’ailleurs être en train de sonner à la porte. »
Notre visiteur était un jeune homme qui avait une allure très athlétique avec son polo et son visage bronzé. Après les présentations, il exposa son problème.
« La femme que j’aime étudie la littérature grecque. Elle a parfois d’étranges exigences. La dernière en date est de me demander de résoudre une énigme adaptée de ses recherches. Elle m’épousera si je peux répondre à trois questions. Acceptez-vous de m’écouter ?

© Inria / Photo Christian Tourniaire.
– Bien sûr. Allez-y.
– Cela se passe à une soirée. Tous les invités ont serré la main de trois des autres invités, sauf un qui n’a serré la main qu’à une personne.
Ce sont là toutes les informations que vous aurez, Dr Ecco. Voici les trois questions :
- Quel est le plus petit nombre possible de gens qui pourraient assister à cette soirée ?
- Pourrait-il y avoir vingt et un invités à cette soirée ?
- Peut-on dégager un schéma général pour déterminer le nombre de gens qui pourraient assister à cette soirée ? »
Pouvez-vous répondre à ces questions ?
Il fallut près d’une journée à Ecco pour répondre aux trois questions. « Le secret, dit-il quand il rappela son client, est de se souvenir que serrer la main de quelqu’un implique une symétrie. Si X serre la main de Y, Y serre la main de X. »
Le jeune homme nota les réponses, remit un chèque à Ecco et prit congé.
Le plus petit chiffre possible est 6. Trois ou moins de trois est impossible, puisque personne n’aurait pu alors serrer la main de trois autres invités. Quatre n’est pas possible, puisque si trois avaient serré la main de trois autres, alors la quatrième personne aurait serré la main des trois autres aussi. Cinq n’est pas possible pour la même raison. Six est possible.
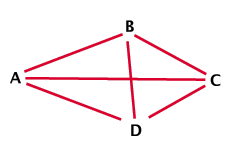
Appelons ces six invités A, B, C, D, E et F. Voici les poignées de main possibles : A et B, B et C, C et D, D et E, E et F, A et C, A et E, et enfin B et D.
 |
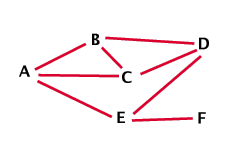 |
| Le nombre des invités doit être supérieur à quatre. Si A, B et C serrent la main de trois autres personnes, c’est aussi le cas de D. Il peut y avoir six invités. | |
Non, il ne pourrait pas y avoir vingt et un invités à une telle soirée ; le nombre des invités ne peut être que pair. Chaque fois que deux personnes se serrent la main, chaque personne ajoute un au nombre de personnes à qui elle a serré la main. Le nombre total de poignées de main a donc augmenté de 2 (une par personne), il reste pair. Si les invités étaient vingt et un, le nombre total de poignées de main serait de 20 x 3 + 1 = 61. Mais c’est impossible.
Oui, on peut dégager un schéma général. Tout nombre pair supérieur à six est possible. Aucun nombre impair ne convient.
Il est facile de voir que six plus tout multiple de quatre marchera, puisque nous pourrions utiliser la solution de la question 1. pour montrer que six satisfait les propriétés et poser que chaque groupe supplémentaire de quatre personnes n’a en fait serré la main qu’à des personnes de ce groupe.
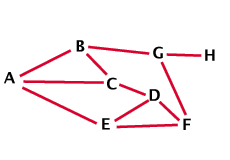
Pour voir si huit plus tout multiple de quatre marche, notez seulement que s’ils étaient huit, A, B, C, D, E, F, G et H, alors les couples suivants se seraient serré la main : A et B, B et C, C et D, D et E, E et F, F et G, G et H, A et C, A et E, B et G, D et F.
« Pourquoi la jeune femme mentirait-elle à son ami au sujet de l’origine de l’énigme ? dit alors Ecco. Les questions sont difficiles, certes, mais elles ne sont pas dans le style de la mythologie grecque. »
Ecco réfléchit plusieurs minutes. « Mais bien sûr… l’oracle de Delphes posait souvent des questions auxquelles on n’était pas censé répondre. Y réfléchir aidait celui qui les entendait. Notre jeune ami était censé échouer. Dans sa tentative, il devait se rendre compte qu’il n’était pas fait pour elle. Voilà le lien entre ces questions et les énigmes mythologiques. Ah ! professeur, ai-je commis une erreur ?
– Vous aurez au moins donné une leçon à cette jeune femme. Les choses ont changé au cours des trois derniers millénaires, et elle devrait le savoir. Les Grecs n’avaient pas d’omniheuristes sous la main ! »
Cette énigme montre une utilisation élémentaire de la théorie des graphes, qui sont l’outil mathématique privilégié pour modéliser toutes sortes de réseaux.
Cette énigme a été publiée dans le livre Les Aventures extraordinaires du Docteur Ecco, Éditions Odile Jacob, nouvelle édition juin 2006.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Dennis Shasha