La tour de Lego

© INRIA / Photo Christian Tourniaire

Ecco avait déjà une solide clientèle quand je l’ai revu. Mais une question ne cessait de me hanter : comment avait-il créé son cabinet d’omniheuriste, profession tellement nouvelle qu’il avait dû en inventer le nom ? Comment parvenait-il à convaincre quelqu’un de faire appel à ses services ? Tout cela me paraissait fort mystérieux. Mais pour Ecco, se constituer une clientèle n’avait jamais été qu’une énigme de plus à résoudre.

« Toute personne exerçant une profession indépendante finit par trouver des clients grâce à ses références ou à la célébrité », m’expliqua Ecco le jour où je trouvai le courage de lui poser la question. Premièrement, il faut que les clients potentiels soient disposés à se lancer dans l’inconnu et, deuxièmement, il faut qu’ils n’aient pas le choix. La première condition exclut les ronds-de-cuir timorés du gouvernement et du monde des affaires. La seconde implique que les clients potentiels n’aient en fait besoin que d’un soupçon d’encouragement pour faire appel à moi. Les gens désespérés sont prêts à se raccrocher à n’importe quel espoir, aussi bizarroïde soit-il. Pensez à la vogue que connaissent les charlatans religieux.

« J’ai donc passé une petite annonce dans plusieurs périodiques soigneusement choisis, des journaux internationaux et des revues d’anciens élèves de certaines universités. Je ne l’ai guère fait plus de deux douzaines de fois dans ma carrière. Le bouche-à-oreille a fait le reste. »

Ecco me montra le texte de l’annonce :

« Elle me paraît un peu courte. Mais elle a porté ses fruits, dites-vous ?

— Superbement. Mais cela ne s’est pas fait tout seul. Une des revues a rechigné à publier une annonce aussi « énigmatique ». La rédaction a exigé une copie de mon doctorat avant d’accepter de publier quoi que ce soit suggérant un savoir-faire mathématique. (J’avais fini mes études à ce moment-là). Un autre magazine a omis le terme « mathématique », si bien que j’ai commencé à recevoir des demandes de gens tentant de surmonter des crises existentielles. Je leur ai recommandé un séjour à San Gimigniano. »

L’un des premiers clients d’Ecco avait été un excentrique, le célèbre milliardaire Hank Alfred. Ecco me raconta l’histoire avec un certain amusement.

« À l’époque, je vivais encore dans une résidence universitaire. Un dimanche après-midi, j’étais sur la piste d’une preuve combinatoire quand des coups frappés à ma porte, avec une canne apparemment, me tirèrent de mes réflexions. Mon visiteur, un homme assez âgé, entra d’un pas décidé, tenant comme un sceptre la canne qu’il avait à la main. »

« Jacob Ecco, je m’appelle Hank Alfred, me dit-il en me serrant vigoureusement la main. J’ai bien l’intention de laisser une trace dans l’histoire. Je veux construire une tour d’un kilomètre de haut. J’aimerais la construire vite, en un an si possible. Peu m’importe que quelqu’un y habite un jour, l’important pour moi est de la construire. J’ai le terrain (une plaine désertique), la technologie et l’argent. Il me manque seulement la méthode. Aidez-moi, Ecco, et vous serez un homme riche. »

« M. Alfred m’a immédiatement plu et son problème ne manquait pas de piquant. Ma seule inquiétude était de me retrouver dans le Guiness des records. Mais M. Alfred m’assura l’anonymat. »

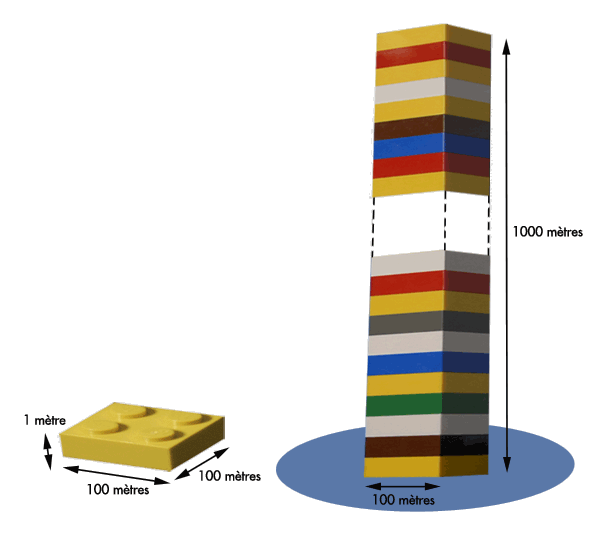
En empilant 1 000 plaques, le millionnaire Hank Alfred se propose de construire une tour d’un kilomètre de haut.

« Je vous résume la situation, poursuivit-il. Nous avons des plaques préfabriquées qui s’emboîtent les unes dans les autres comme les pièces de Lego de ma petite-fille. Chacune est un carré de 100 mètres de côté et de 1 mètre d’épaisseur. Ces plaques sont munies de coupleurs sur les deux faces qui leur permettent de s’accrocher les unes aux autres. D’après mes ingénieurs, il est possible de les empiler sur un kilomètre de haut si on le souhaite. Elles sont si légères qu’un élévateur conçu pour cela peut soulever une pile de 5 000 plaques pour la poser sur une autre. Je peux vous fournir autant d’élévateurs que vous voulez. Placer une plaque sur une autre prend une semaine. Placer une pile sur une autre prend également une semaine, mais si une des deux piles mesure plus de 100 mètres de haut, il faut compter une semaine supplémentaire pour la monter. Je ne reculerai devant aucune dépense. En combien de temps pouvons-nous faire cela au plus vite ? »

Sachant que les ressources sont illimitées, en commençant par les plaques non empilées, avec quelle rapidité une équipe peut-elle construire ce kilomètre vertical ? (Proposez un calendrier.)