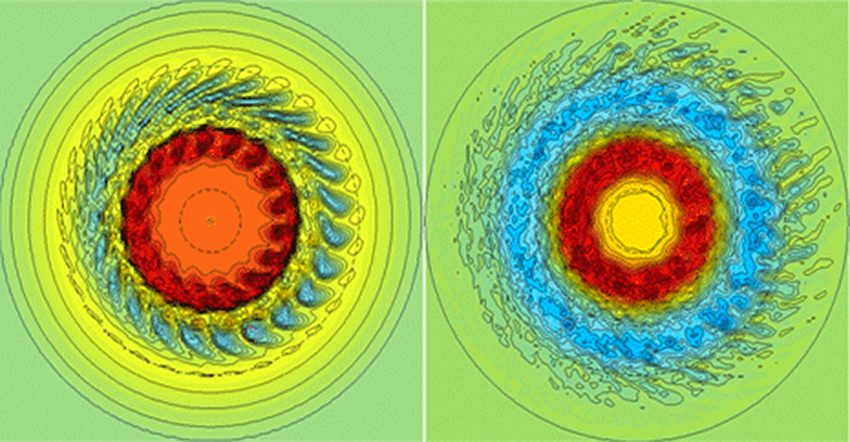
La turbulence dans les plasmas

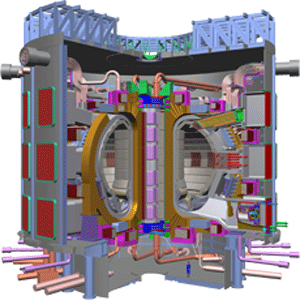
Maquette d’ITER, en cours de construction à Cadarache.
Image : © ITER

Le 21 novembre 2006, les représentants de l’Union Européenne, du Japon, de la Chine, de la Russie, de la Corée du Sud, de l’Inde et des États-Unis ont signé l’accord établissant l’organisation internationale qui aura pour mission d’implémenter le projet ITER pour l’énergie de fusion qui sera construit à Cadarache, dans le Sud de la France. Ce sont donc des scientifiques et ingénieurs de pays représentant plus de la moitié de la population mondiale qui unissent leurs efforts pour obtenir une source d’énergie primaire quasi inépuisable et aux effets environnementaux bénins. Estimé à cinq milliards d’euros, ce projet constitue le second projet international par la taille – après la Station spatiale internationale – et cette taille est précisément une des raisons pour lesquelles il a été considéré judicieux d’unir les forces au niveau planétaire.

Pourquoi la réalisation de la fusion sur la Terre nécessite-t-elle des moyens aussi importants ? Pourquoi ITER est-il si gros ? En un mot : à cause de la turbulence. La turbulence impose des contraintes sur la taille d’un réacteur comme ITER. Son étude nécessite l’élaboration de simulations numériques fines, que nous allons décrire. Mais avant, faisons un petit détour par le cosmos afin de comprendre ce qu’est la fusion nucléaire.

Notre Soleil brille grâce à l’énergie de fusion. Il est constitué principalement d’hydrogène, confiné à des pressions gigantesques par son propre poids : la température au centre de cet astre atteint 15 millions de degrés et la densité est 150 fois celle de l’eau, résultant en une pression de 200 milliards d’atmosphères. Par une succession de réactions de fusion et de désintégrations nucléaires, l’hydrogène se transforme en hélium, en dégageant une énergie gigantesque. Mais le processus est extrêmement lent : il faudrait environ dix milliards d’années pour que le Soleil épuise son combustible hydrogène. Cette lenteur nous est bénéfique : sans elle, le Soleil se serait déjà éteint bien avant que la vie ait eu une chance d’apparaître sur la Terre. Elle est due à la très faible probabilité que l’hydrogène fusionne, même aux conditions extrêmes qui règnent au sein de l’astre du jour. Autrement dit, si l’on veut faire de la fusion sur la Terre, on doit utiliser d’autres phénomènes que ceux régnant à l’intérieur du Soleil.

Deux choses vont nous aider : d’abord l’existence d’isotopes de l’hydrogène, le deutérium et le tritium, qui ont une probabilité de fusionner plus élevée que l’hydrogène lui-même ; puis les champs magnétiques, qui ont la propriété de confiner les particules chargées.

La vitesse de la réaction de fusion du deutérium et du tritium est maximale lorsque la température atteint plusieurs centaines de millions de degrés. Dans ces conditions, toute matière est à l’état de plasma, c’est-à-dire que l’énergie cinétique (énergie d’un corps en mouvement) des particules est suffisante pour arracher les électrons aux noyaux atomiques. Le plasma, aussi appelé gaz ionisé, ressemble à une « soupe » constituée de deux ingrédients fondamentaux : les ions, chargés positivement, et les électrons, chargés négativement. La force attractive entre les particules des deux types est telle que les charges positives et négatives tendent à se mêler en un ensemble quasi neutre à l’échelle macroscopique.

Une bonne bouteille magnétique

Le fait que les particules du plasma soient chargées a des conséquences à la fois bénéfiques et maléfiques. Examinons d’abord le côté positif de la médaille. Placée dans un champ magnétique, toute particule chargée effectue un mouvement en hélice qui s’enroule autour des lignes de champ. Le rayon de giration, appelé aussi rayon de Larmor, est de l’ordre de quelques millimètres pour un ion hydrogène et d’une fraction de millimètre pour un électron, pour les valeurs de champ magnétique et les températures envisagées dans ITER. Ainsi, le mouvement des particules dans un champ magnétique est confiné, comme des perles sur un fil. Pour ne pas perdre les perles, la première idée est de refermer le collier. On fait de même avec le champ magnétique. Cependant, à cause de la courbure du champ magnétique qui en résulte, les particules ne suivent plus exactement leur ligne de champ, mais dérivent lentement dans la direction perpendiculaire au champ et au gradient de l’intensité de ce champ : le champ magnétique est plus intense à l’intérieur de l’anneau qu’à l’extérieur. Cette dérive a lieu dans des directions opposées pour les particules des deux signes, et si rien d’autre n’était fait, il y aurait séparation des charges, donc apparition d’un champ électrique, ce qui finirait par expulser les particules hors des lignes de champ.

Pour empêcher cette ségrégation des charges, l’idée est de créer une composante hélicoïdale au champ magnétique, de telle sorte que les particules dérivent tantôt d’un côté de la ligne de champ, tantôt de l’autre, et donc d’éviter qu’elles ne s’écartent trop de leur chemin initial. La configuration résultante est en forme d’anneau, les lignes de champ s’enroulant sur des surfaces imbriquées, appelées surfaces magnétiques.

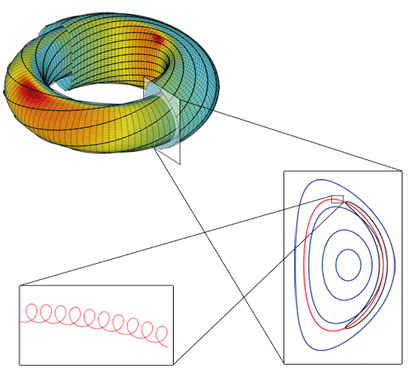
Configuration d’un tokamak : les lignes de champ magnétique s’enroulent en hélice sur des surfaces magnétiques imbriquées en couches superposées (en haut). Dans une vue en coupe (en bas à droite), les trajectoires des particules, l’une piégée (en noir), l’autre passante (en rouge), dérivent hors des surfaces magnétiques (en bleu), mais restent confinées. Une vue de détail (en bas à gauche) montre la trajectoire d’une particule. Images : L. Villard

Dans ce qui suit, nous considérerons le cas du tokamak (acronyme russe signifiant chambre torique — c’est-à-dire en forme de tore — dans des bobines magnétiques), qui consiste à créer cette torsion hélicoïdale, ou transformée rotationnelle, des lignes de champ en faisant passer un courant électrique dans le plasma. Nous avons ainsi une « bouteille magnétique », une sorte de contenant dans lequel les parois en verre seraient remplacées par un champ magnétique, qui a la propriété de confiner les particules chargées du plasma. Une « bonne bouteille » est ainsi caractérisée par un champ magnétique suffisamment fort pour avoir des rayons de giration petits et une torsion suffisante, donc un courant plasma suffisamment élevé. Ainsi, le champ magnétique au cœur d’ITER sera de 5,3 teslas (ce qui représente 100 000 fois le champ magnétique terrestre) et le courant plasma atteindra 15 millions d’ampères.

Le revers de la médaille

Cependant, les particules du plasma ne sont pas isolées : il en faut un nombre suffisant, assez chaudes et pendant un temps assez long pour que les réactions de fusion libèrent suffisamment d’énergie dans le plasma. En effet, même si une bouteille magnétique est en mesure de confiner quelques particules individuelles, le confinement d’un grand nombre de ces particules n’est pas garanti, car les interactions électromagnétiques peuvent prendre la forme d’effets collectifs.

De même que le comportement d’un individu pris dans un mouvement de foule peut être très différent de celui qu’il aurait s’il était seul, de nombreuses ondes et instabilités peuvent modifier de façon importante le comportement des particules du plasma. Parmi ces instabilités, les instabilités magnétohydrodynamiques (provoquées par les fluides en mouvement dans un champ magnétique) sont si violentes qu’elles peuvent conduire à la perte totale du plasma ; pour les éviter, on doit limiter la pression et le courant dans un tokamak. On sait aujourd’hui calculer ces limites, notamment grâce aux travaux de l’équipe de Francis Troyon, du Centre de recherches en physique des plasmas de l’École polytechnique fédérale de Lausanne, au début des années 1980.

Même si l’on sait maintenant contrôler un tokamak en évitant ces limites « dures », il subsiste une famille d’instabilités dans de tels plasmas. Elles sont dues à la présence de gradients de température, de densité et de champ magnétique. Lorsque le gradient de température excède une valeur critique, une instabilité apparaît, à l’image de ce qui se passe pour un tas de sable, dont la pente ne peut être plus raide qu’une certaine valeur.

Dans les plasmas qui nous concernent, la plupart de ces instabilités sont électrostatiques, c’est-à-dire que l’effet des perturbations sur le champ magnétique est faible et peut être négligé. Ces instabilités se développent jusqu’à former un état turbulent dont l’effet est de « brasser » les particules chaudes du centre du plasma avec celles plus excentrées et plus froides : ce flux de chaleur dégrade la qualité de confinement de l’énergie et des particules. Il s’effectue alors une perte du pouvoir isolant thermique. Pour vous donner une image, considérons les surfaces magnétiques imbriquées comme des couches successives de vêtements : imaginez que vous vous trouvez en plein hiver en Sibérie par – 50 degrés. Vous aimeriez que la température du corps, au centre des habits, puisse rester suffisamment chaude quand le bord est glacial. Si vos habits sont faits d’un matériau bien isolant, vous avez besoin d’une épaisseur moindre que s’ils sont constitués d’un mauvais isolant ou troués voire déchirés. L’« épaisseur » des habits représente la taille du plasma. Plus les couches sont nombreuses, meilleure est l’isolation thermique. L’effet de la turbulence peut être assimilé à des déchirures dans les couches d’habits qui laissent ainsi passer des courants d’air. On a besoin de plus de couches d’habits pour se maintenir au chaud lorsque ceux-ci sont troués que dans le cas contraire. Les simulations numériques directes permettent de calculer comment le flux de chaleur dû à la turbulence varie avec la taille du plasma. La diffusivité diminue avec la taille du plasma, plus exactement avec le rapport entre le rayon du plasma et le rayon de giration des particules. Le pouvoir confinant du champ magnétique est extraordinaire, et ce malgré la présence de turbulence : dans ITER, les électrons parcourront en moyenne 150 000 kilomètres avant de perdre leur énergie, et ceci dans un « grand » plasma de 16,4 mètres de taille. S’il n’y avait pas de turbulence toutefois, la taille du plasma nécessaire à la fusion serait bien plus petite.

Le plasma au cœur d’ITER sera un million de fois plus chaud que la température ambiante, mais aura une densité plusieurs centaines de milliers de fois plus faible que l’air, résultant en une pression de quelques atmosphères seulement, soit la pression de gonflage d’un pneu de vélo… On est donc bien loin des conditions régnant au cœur du Soleil ! Dans tous les plasmas confinés par des champs magnétiques, il existe en effet une limite de pression au-delà de laquelle des instabilités globales se déclenchent. Ce sont des instabilités macroscopiques — c’est-à-dire à grande échelle, par opposition aux instabilités responsables de la turbulence dont il est question dans cet article, qui sont, elles, à l’échelle microscopique — et leur effet est pire qu’une augmentation de turbulence, car elles peuvent conduire à la perte totale du plasma, qui sort de sa bouteille magnétique.

On prédit le temps de confinement —  c’est le temps moyen pendant lequel l’énergie reste à l’intérieur du système — d’ITER à partir des extrapolations des résultats des expériences existantes. Grâce aux développements de la simulation numérique, est apparue la possibilité de calculer la turbulence dans les plasmas directement à partir des équations fondamentales. Mais la difficulté est considérable : les échelles de temps du système varient de la nanoseconde à plusieurs secondes ; les échelles d’espace vont de quelques micromètres à plusieurs mètres, et sont différentes pour les deux espèces (ions et électrons). En outre, le plasma présente une très forte anisotropie, c’est-à-dire que ses propriétés varient en fonction de la direction considérée. Cette anisotropie est due à la présence du champ magnétique qui est le siège de nombreux phénomènes non linéaires.

Dans un plasma de fusion magnétique, une particule parcourt plusieurs fois la machine entière avant que l’effet des collisions avec les autres particules ne soit mesurable : ce sont des conditions très différentes des gaz neutres que nous rencontrons dans la vie courante, par exemple l’air ambiant, dont les molécules subissent des milliers de collisions chaque millimètre de leur parcours. Ceci a pour conséquence la sensibilité des particules du plasma à la géométrie de la configuration magnétique. Celle-ci influe sur les instabilités, le niveau de turbulence et finalement la qualité du confinement. D’autre part, les modèles fluides, décrivant l’évolution dans l’espace et le temps de quantités locales moyennes, sont impuissants à décrire nombre de phénomènes qui dépendent de la distribution en vitesses des particules. Pour ces phénomènes, on a donc besoin d’une théorie cinétique, que nous allons considérer.

Le décompte des paramètres

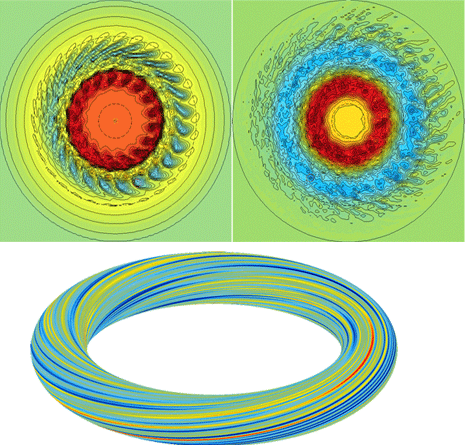
Simulations de la turbulence. Les perturbations du potentiel électrostatique sont représentées dans des couleurs allant du bleu pour la valeur minimale au rouge pour la valeur maximale. Deux vues en coupe (en haut), perpendiculaires au champ magnétique, prises à des instants différents, montrent le développement de perturbations de courte longueur d’onde par rapport aux dimensions du tokamak. La figure en haut à gauche se situe à une phase plus précoce du développement de la turbulence. La vue tridimensionnelle (en bas) d’une surface magnétique montre que les perturbations forment des structures alignées avec le champ magnétique, dont les lignes de champ sont représentées sur la figure « Configuration d’un tokamak » (voir plus haut). Images : L. Villard

Le plasma comporte de l’ordre de 10²³ particules, et il est totalement irréaliste de calculer le mouvement de chacune d’elles. On remplace, dans la description cinétique, les particules individuelles par une fonction de distribution, dont la valeur représente la densité de probabilité qu’une particule ait une position et une vitesse données. Il y a trois composantes de la position et trois composantes de la vitesse, si bien que les fonctions de distribution sont définies dans un espace à six dimensions. Or, il s’avère que la turbulence qui est responsable de l’essentiel du flux de chaleur, est due à des perturbations à des fréquences bien inférieures à la fréquence de giration des particules du plasma. Cela a conduit au développement de la théorie gyrocinétique, dans laquelle on effectue analytiquement une moyenne temporelle sur le mouvement de giration. Il reste donc trois dimensions d’espace, deux dimensions de vitesses (parallèle et perpendiculaire au champ magnétique), et le temps. À chaque instant t, la particule est donc représentée par un point dans un espace à 5 dimensions.

Une caractéristique fondamentale du plasma est la forte anisotropie due au champ magnétique : le mouvement parallèle des ions est environ 100 fois plus rapide que celui de dérive perpendiculaire et, pour les électrons, ce rapport s’élève à plusieurs milliers. En conséquence, les perturbations ont tendance à être alignées avec le champ magnétique : les longueurs d’onde parallèles au champ sont de l’ordre de la taille du plasma, alors que les longueurs d’onde perpendiculaires peuvent être aussi petites que le rayon de giration.

Les équations que nous devons résoudre découlent des équations fondamentales de la physique classique : celles de Newton pour la dynamique et de Maxwell pour l’électromagnétisme. Elles sont écrites pour des champs continus. Avant de résoudre ces équations avec un ordinateur, il faut les discrétiser, c’est-à-dire remplacer la description continue des quantités par un ensemble fini, et remplacer les opérateurs de différentiation et d’intégration par des opérations arithmétiques et logiques, qui sont à ce jour les seules qu’un processeur sache effectuer.

Les radars d’Euler ou les mouchards de Lagrange

Il existe deux méthodes de discrétisation des champs continus. Par analogie, imaginons que l’on veuille déterminer le flux de circulation automobile sur un réseau routier. L’approche eulérienne (du mathématicien suisse Leonhard Euler (1707-1783)) consiste à placer des radars fixes partout le long des routes. L’approche lagrangienne (du mathématicien français Joseph-Louis Lagrange (1736-1813)) consiste à placer des mouchards sur chaque véhicule. Dans les deux cas, on peut reconstruire toute l’information nécessaire pour obtenir une image précise du trafic.

Pour notre plasma, la méthode d’Euler revient à définir un ensemble de points sur un maillage fixe de l’espace 5D, et de considérer les valeurs de la fonction de distribution des particules aux nœuds du maillage, les valeurs intermédiaires étant obtenues par interpolation. Dans la méthode lagrangienne, on choisit des particules à des conditions initiales fixées dans l’espace 5D, puis on suit leur déplacement en intégrant dans le temps les équations du mouvement. À chaque pas temporel, on calcule la perturbation de densité à partir des positions instantanées. Dans les deux cas (Euler et Lagrange), cette densité perturbée intervient alors dans la résolution des équations du champ. Les résultats présentés dans cet article ont été obtenus avec l’approche lagrangienne.

On utilise un échantillonnage des fonctions de distribution, la taille de l’échantillon étant limitée par la mémoire disponible et par le temps de calcul nécessaire à l’intégration des trajectoires. Un élément de l’échantillon n’est pas une particule réelle du plasma, mais « représente » en quelque sorte une portion de l’espace 5D. On parle de « marqueur » de l’espace 5D, ou de « pseudo-particule », ou encore de « particule » par abus de langage.

Résoudre sans faire de bruit

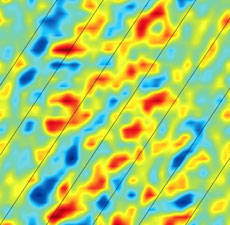
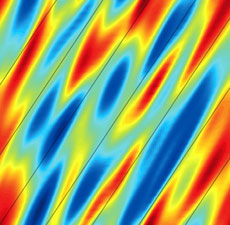
Détails de la turbulence simulée sur une surface magnétique. À gauche, les perturbations se noient dans le « bruit numérique ». À droite, de nouvelles méthodes numériques de filtrage ont permis d’éliminer ce comportement non physique. Images : L. Villard

Bien sûr, plus nombreuses sont les « particules » du modèle, meilleure sera la description. Combien faut-il de « particules » pour simuler la turbulence dans un tokamak ? La méthode d’échantillonnage a le désavantage de fournir un résultat dont l’erreur statistique, appelée aussi « bruit numérique », décroît très lentement avec le nombre de « particules ».

Un progrès important vers une meilleure précision des modèles a été accompli au début des années 1990, quand on n’a échantillonné que la partie perturbée de la fonction de distribution, la partie d’équilibre étant traitée analytiquement.

Un deuxième pas a été franchi lorsque nous avons, pour la première fois, introduit dans un programme de calcul numérique global un système d’équations gyrocinétiques qui conserve l’énergie : c’est une propriété importante des équations de base, et elle nous sert à évaluer la qualité numérique des simulations. De plus, ce programme tient compte de la géométrie exacte et globale du champ magnétique.

Un troisième pas a consisté à effectuer une première simulation pour obtenir la distribution optimale, du point de vue statistique, des conditions initiales ; l’idée était de peupler densément les régions de l’espace 5D où les perturbations seraient importantes.

Nous venons de franchir une quatrième étape : nous avons réduit une des causes majeures du bruit numérique grâce à une méthode de filtrage des perturbations dans la direction des lignes de champ magnétique. Cette méthode a permis d’augmenter la taille du pas temporel d’un ordre de grandeur, et donc d’obtenir des simulations plus longues, tout en améliorant la conservation de l’énergie et la convergence numérique.

Malgré ces améliorations, on estime qu’il faudra des milliards de « particules » pour simuler tout le plasma d’ITER. À ce jour, une telle simulation n’a pas encore été faite. Cependant, nous pouvons déjà simuler des plasmas de tokamaks existants, pour lesquels un cas test, appelé CYCLONE, a été défini afin de comparer les théories et programmes numériques avec l’expérience.

Les ordinateurs les plus puissants aujourd’hui sont constitués d’un grand nombre de processeurs reliés par un réseau de connexions rapides, le plus performant étant actuellement un IBM Blue Gene, à 131 072 processeurs. Les algorithmes utilisés doivent s’adapter à cette architecture : il s’agit de répartir les opérations de telle sorte que tous les processeurs soient simultanément occupés. On parle de parallélisme massif. Le défi est d’obtenir un programme dont la performance croît linéairement avec le nombre de processeurs. Cela n’est pas banal, car il faut veiller à ce que les communications entre processeurs ne ralentissent pas trop l’exécution. Nous avons introduit un double parallélisme : le domaine est découpé en tranches et chaque tranche est clonée. Une simulation globale complète d’un cas CYCLONE, sur 1 024 processeurs de l’IBM Blue Gene/L de l’École polytechnique fédérale de Lausanne, prend environ huit heures. Il faudra donc plusieurs milliers de processeurs et plusieurs jours pour simuler tout le cœur d’ITER !

Des cascades et des avalanches

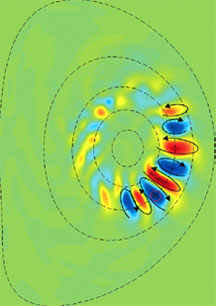
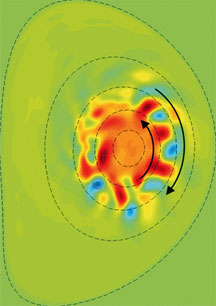
Les écoulements zonaux ont un effet régulateur sur la turbulence. Les perturbations turbulentes ont pour conséquence un mouvement radial de brassage (flèches sur l’image de gauche) entre les régions chaudes du centre et les régions plus froides de la périphérie. Les écoulements zonaux se caractérisent en revanche par un mouvement transverse (flèches sur l’image de droite), qui cisaille les perturbations turbulentes et réduit ainsi le flux de chaleur entre le centre chaud et la périphérie froide. Images : L. Villard

Les simulations numériques directes de la turbulence dans les plasmas confinés magnétiquement ont donné des résultats intéressants. Partant d’une condition initiale avec un gradient de température donné, les modes instables croissent rapidement. Par couplage non linéaire, ils créent une composante appelée zonale, dont le mouvement associé consiste en une alternance de bandes de directions opposées. Ce mouvement cisaille les perturbations instables et diminue ainsi le transport d’énergie. Les écoulements zonaux ont alors un effet régulateur sur la turbulence. La création d’une structure zonale à partir de la turbulence est un exemple de cascade inverse et d’auto-organisation, où des perturbations de courte longueur d’onde se couplent pour former des grandes structures cohérentes. De tels phénomènes sont observés dans la nature, par exemple la structure en bandes de l’atmosphère de Jupiter ou encore les « jet streams », des zones de vents rapides dans la haute atmosphère qui apparaissent à la limite entre des masses d’air subtropicales chaudes et polaires froides ; ces vents orientés d’Ouest en Est sont perpendiculaires au gradient de température Nord-Sud.

Les écoulements zonaux régulent la turbulence grâce à deux mécanismes fondamentaux. Premièrement, ils sont engendrés par un transfert d’énergie des modes instables, et ainsi soustraient de l’énergie de la turbulence, alors qu’eux-mêmes ne transportent pas de flux de chaleur puisqu’ils sont perpendiculaires au gradient de température. Deuxièmement, ils cisaillent les structures turbulentes et réduisent ainsi le transport de chaleur causé par ces structures. Pour comprendre cet effet, imaginons qu’une foule de gens (symbolisant la turbulence à petite échelle) souhaite traverser une route parcourue par des véhicules dans les deux sens (symbolisant les écoulements zonaux) ; le flux des piétons est fortement ralenti par la présence du trafic. Quand on supprime artificiellement les écoulements zonaux dans les simulations, on obtient des flux de chaleur trois à cinq fois plus élevés, ce qui confirme leur rôle dans la détermination du niveau de turbulence.

Nous avons observé que lorsque le gradient de température est bien au-dessus de la valeur critique du seuil d’instabilité, un phénomène d’avalanches se produit : il y a une succession d’effondrements du gradient de température, causée par de brusques jaillissements de turbulence. Celle-ci est immédiatement suivie par des montées d’écoulements zonaux qui réduisent localement et momentanément la turbulence. Après plusieurs avalanches, le profil de température est réduit partout, à des valeurs proches du seuil d’instabilité, et une accalmie de la turbulence s’ensuit.

L’effet bénéfique du courant

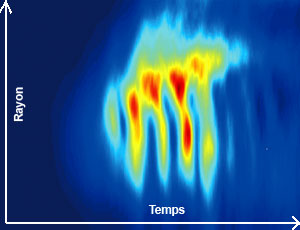
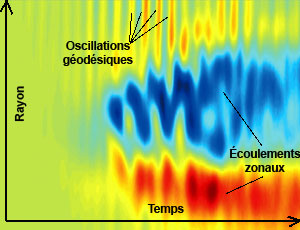
Jaillissements de turbulence. On a représenté, en fonction du temps sur 150 microsecondes et du rayon sur 24 centimètres, le flux de chaleur (à gauche, du bleu pour un flux nul au rouge pour un flux maximal) et la vitesse des perturbations (à droite, du bleu pour une vitesse minimale au rouge pour une vitesse maximale). Les deux images montrent une périodicité équivalente. Les écoulements zonaux forment de larges bandes horizontales. Les oscillations géodésiques se manifestent par d’étroites bandes verticales. Images : L. Villard

Les perturbations zonales peuvent aussi osciller au cours du temps ; leur fréquence est due à la courbure dite « géodésique » des lignes de champ magnétique.

Nous avons observé que la turbulence peut exciter de telles oscillations. Les écoulements zonaux oscillants réduisent la turbulence moins efficacement que la composante stationnaire : les structures turbulentes n’ont pas le temps d’être complètement cisaillées avant que le sens du cisaillement ne s’inverse. Nos résultats indiquent que ces oscillations géodésiques ont une amplitude d’autant plus faible que la torsion des lignes de champ magnétique est grande. Dans un tokamak, cette torsion est due au courant circulant dans le plasma. Nous avons montré, avec une série de simulations numériques directes globales, que le flux de chaleur dû à la turbulence est inversement proportionnel au courant plasma ; autrement dit, plus le courant est élevé dans un tokamak, meilleur est le temps de confinement de l’énergie. Or, les lois d’échelles empiriques, obtenues sur la base des résultats expérimentaux, et sur lesquelles repose l’architecture d’ITER, montrent également un effet favorable du courant sur le confinement.

Avec les progrès de la théorie, des méthodes numériques et des performances des ordinateurs, on envisage d’inclure à l’avenir de plus en plus d’effets physiques dans les simulations, afin de les rendre plus proches de la réalité. Mais la comparaison avec l’expérience n’est pas facile, car la réalité est bien plus complexe que ne le sont les effets physiques pris en charge dans les modèles. Cependant, la simulation numérique nous permet d’observer des phénomènes physiques avec un niveau de détail bien supérieur à celui qui peut être mesuré expérimentalement. On n’a observé que très récemment des écoulements zonaux et des oscillations géodésiques au cœur d’un tokamak. Un des objectifs sera aussi de développer des techniques de mesure toujours plus fines, pour les comparer aux prédictions théoriques. Le chemin (iter en latin) est encore long, mais s’annonce passionnant.

Une première version de cet article est parue dans le dossier n°52 La modélisation informatique, exploration du réel de la revue Pour la Science, numéro de juillet/septembre 2006.