Le problème du voyageur de commerce
C’est déjà sous forme de jeu que William Rowan Hamilton a posé pour la première fois ce problème, dès 1859. Sous sa forme la plus classique, son énoncé est le suivant : « Un voyageur de commerce doit visiter une et une seule fois un nombre fini de villes et revenir à son point d’origine. Trouvez l’ordre de visite des villes qui minimise la distance totale parcourue par le voyageur ». Ce problème d’optimisation combinatoire appartient à la classe des problèmes NP-Complets.
Les domaines d’application sont nombreux : problèmes de logistique, de transport aussi bien de marchandises que de personnes, et plus largement toutes sortes de problèmes d’ordonnancement. Certains problèmes rencontrés dans l’industrie se modélisent sous la forme d’un problème de voyageur de commerce, comme l’optimisation de trajectoires de machines outils : comment percer plusieurs points sur une carte électronique le plus vite possible ?
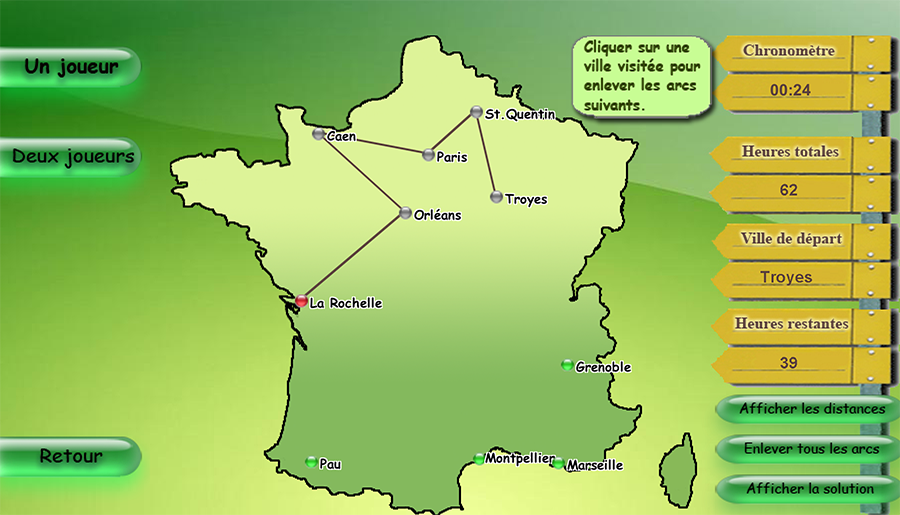
Comme illustration de ce problème, nous vous proposons le jeu ci-dessous. Le but ? Trouver le parcours du voyageur pour qu’il visite toutes les villes de France affichées, en respectant la durée maximale du voyage, exprimée en heures. Le nombre de villes à visiter dépend de la difficulté choisie. En mode deux joueurs, si les parcours trouvés ont la même durée, le gagnant sera celui qui aura trouvé la solution le plus rapidement.
Cette animation a été réalisée par Ouest INSA, à partir de l’applet réalisée dans le cadre d’un projet étudiant de l’École Polytechnique de l’Université de Tours, par Li Yifang, encadrée par Yannick Kergosien et Jean-Charles Billaut.
Comme vous avez pu le remarquer, le niveau expert peut être très difficile, même pour peu de villes. Dès que le nombre de villes augmente, ce problème devient rapidement impossible à résoudre de tête. Même les meilleurs algorithmes en informatique ont leurs limites lorsque le nombre de villes devient vraiment très grand.
Pour un nombre de villes égal à N, le nombre de parcours possibles est égal à (N-1)!/2 = [(N-1)(N-2)(N-3)…1]/2. Par exemple, pour 5 villes, le nombre de parcours est égal à 12, mais pour 10, il est déjà de 181 440 et pour 20, il est d’environ 60 × 1015. Supposons un ordinateur assez rapide pour évaluer un parcours en une demi-microseconde : le cas à 5 villes serait résolu en moins de 6 microsecondes, le cas à 10 villes en 0,09 secondes, mais il faudrait 964 ans pour résoudre le cas à 20 villes en balayant toutes les solutions possibles. C’est pourquoi il est indispensable d’élaborer des techniques performantes de résolution pour trouver rapidement la meilleure solution, ou du moins une solution de bonne qualité.
Représentation du problème
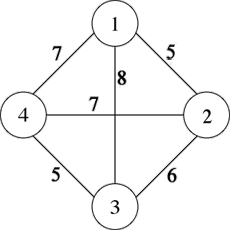
Exemple de graphe à 4 sommets.
Le problème du voyageur de commerce peut être modélisé à l’aide d’un graphe constitué d’un ensemble de sommets et d’un ensemble d’arêtes. Chaque sommet représente une ville, une arête symbolise le passage d’une ville à une autre, et on lui associe un poids pouvant représenter une distance, un temps de parcours ou encore un coût. Ci-contre, un exemple de graphe à 4 sommets.
Résoudre le problème du voyageur de commerce revient à trouver dans ce graphe un cycle passant par tous les sommets une unique fois (un tel cycle est dit « hamiltonien ») et qui soit de longueur minimale. Pour le graphe ci-contre, une solution à ce problème serait le cycle 1, 2, 3, 4 et 1, correspondant à une distance totale de 23. Cette solution est optimale, il n’en existe pas de meilleure.
Comme il existe une arête entre chaque paire de sommets, on dit que ce graphe est « complet ». Pour tout graphe, une matrice de poids peut être établie. En lignes figurent les sommets d’origine des arêtes et en colonnes les sommets de destination ; le poids sur chaque arête apparaît à l’intersection de la ligne et de la colonne correspondantes. Pour notre exemple, cette matrice est la suivante :
| 0 | 5 | 8 | 7 |
| 5 | 0 | 6 | 7 |
| 8 | 6 | 0 | 5 |
| 7 | 7 | 5 | 0 |
Dans cet exemple, le graphe est « non orienté », c’est-à-dire qu’une arête peut être parcourue indifféremment dans les deux sens, cela explique que la matrice soit symétrique. Cette symétrie n’est pas forcément respectée dans le cas d’un graphe orienté. Il existe alors deux catégories de problèmes : le cas symétrique (le poids de l’arc du sommet X vers Y est égal au poids de l’arc du sommet Y vers X) et le cas asymétrique (le poids de l’arc du sommet X vers Y peut être différent du poids de l’arc du sommet Y vers X).
Méthodes de résolution
Comme pour le problème du sac à dos (un autre des problèmes les plus connus dans le domaine de l’optimisation combinatoire et de la recherche opérationnelle), il existe deux grandes catégories de méthodes de résolution : les méthodes exactes et les méthodes approchées. Les méthodes exactes permettent d’obtenir une solution optimale à chaque fois, mais le temps de calcul peut être long si le problème est compliqué à résoudre. Les méthodes approchées, encore appelées heuristiques, permettent quant à elles d’obtenir rapidement une solution approchée, mais qui n’est donc pas toujours optimale.
Méthodes exactes
Pour le problème du voyageur de commerce, l’une des méthodes exactes les plus classiques et les plus performantes reste la Procédure par Séparation et Evaluation (PSE). Cette méthode repose sur le parcours d’un arbre de recherche. Dans un chemin de cet arbre, le premier nœud représente la ville de départ, son successeur la deuxième ville visitée, puis la troisième ville visitée, etc. À chaque étape de l’algorithme, on crée autant de nœuds qu’il reste de villes à visiter. À chaque nœud, le choix consiste à sélectionner la prochaine ville à visiter parmi les villes restantes. Ainsi, voici l’arbre de recherche pour l’exemple présenté ci-dessus :
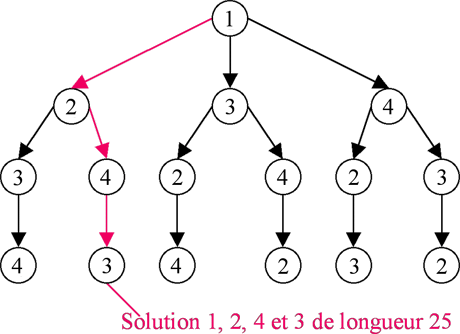
Dans le cas du problème du voyageur de commerce, la fonction objectif à minimiser est la longueur du cycle. La réduction de l’espace de recherche repose sur l’utilisation de bornes inférieures et supérieures. Rappelons que :
-
une borne inférieure est une estimation par défaut de la fonction objectif. Autrement dit, c’est une valeur qui est nécessairement inférieure à la valeur de la meilleure solution possible. Dans notre cas, s’il y a un graphe avec N sommets à traverser, le cycle hamiltonien passera obligatoirement par N arêtes. Ainsi, pour avoir une borne inférieure assez intuitive, il suffit d’additionner le poids des N arêtes possédant les plus petits poids. Même si cette solution a de forts risques de ne pas être réalisable, la valeur de la fonction objectif ne pourra pas être plus petite.
-
une borne supérieure est une estimation par excès de la fonction objectif. Autrement dit, la meilleure solution a nécessairement une valeur plus petite. Dans notre cas, un cycle hamiltonien quelconque dans le graphe fournit une borne supérieure.
Le principe de réduction de l’arbre de recherche consiste à couper l’exploration de l’arbre à la hauteur de certains nœuds. Où faut-il couper l’arbre de recherche ? Supposons que la borne supérieure soit fournie par un algorithme approché – que nous détaillerons plus loin. On examine les nœuds sur les différentes branches, en partant du sommet, pour déterminer une borne inférieure correspondant à chacun des nœuds visités. Pour un nœud donné, on calcule cette borne inférieure en additionnant la somme des poids des arêtes déjà sélectionnées dans le cycle avec la somme des x plus petits poids parmi les arêtes restantes, x étant le nombre d’arêtes manquantes dans le cycle en cours de construction. À partir d’un nœud et de sa borne inférieure, les solutions descendantes de ce nœud ne pourront pas avoir une valeur plus petite que cette borne inférieure. Si jamais, à un nœud donné, la valeur de la borne inférieure excède la valeur de la borne supérieure, alors il est inutile d’explorer les nœuds en dessous de celui-ci. Enfin, la valeur de la borne supérieure peut être actualisée lorsqu’est trouvée une solution réalisable qui possède une valeur plus petite. Ce système de calcul de bornes demande un faible coût en temps de calcul et permet d’augmenter la rapidité de la PSE, puisqu’elle coupe les branches inutiles à explorer.
Les chercheurs ont mis au point différentes techniques pour diminuer la taille de l’arbre et augmenter la rapidité de la PSE. Certaines sont basées sur le choix de l’ordre de visite des villes. Ainsi, une stratégie de recherche qui fonctionne bien pour fixer l’ordre de visite des villes est la règle du plus proche voisin : au nœud correspondant à une ville donnée, la recherche du prochain nœud, c’est-à-dire de la prochaine ville à visiter, commencera par le nœud le plus proche de celui considéré. Elles peuvent aussi reposer sur une évaluation à chaque nœud, ou encore sur des propriétés du problème qui permettent de tirer des conclusions au sujet de certaines villes ou sur des sous-ensembles de villes. C’est une telle démarche qui a été utilisée pour la niveau expert de l’applet.
Méthodes approchées
Dans le cas d’un nombre de villes si grand que même les meilleures méthodes exactes nécessitent un temps beaucoup trop long de résolution, des méthodes approchées, ou algorithmes d’approximation, sont utilisées. Elles permettent d’obtenir en un temps très rapide de bonnes solutions, pas nécessairement optimales, mais d’une qualité suffisante.
Étant donné que le problème du voyageur de commerce a été, et continue à être largement étudié du fait de sa complexité et du nombre important de problèmes dérivés, il existe de nombreux algorithmes d’approximation. Chacun a ses avantages et ses inconvénients. La méthode retenue ne sera pas le même selon que l’on privilégie le temps de calcul, la qualité de la solution, ou encore le choix entre plusieurs solutions.
-
Une famille de méthodes est celle des algorithmes gloutons, dont l’un des plus connus est la méthode par insertion. L’idée est la suivante : le parcours du voyageur de commerce est construit pas à pas en y insérant de nouvelles villes. À un instant donné de l’algorithme, un certain cycle de villes a été construit. L’étape suivante consiste à insérer une ville supplémentaire dans le cycle de manière optimale, c’est-à-dire qu’elle augmente au minimum la longueur totale du cycle. À l’étape initiale de l’algorithme, le parcours de voyageur est composé de deux villes, la ville de départ et celle qui en est la plus proche. L’algorithme se termine lorsque toutes les villes à visiter ont été insérées. Cependant, même si l’insertion d’une ville dans le cycle est optimale et rapide à calculer, la solution finale n’est pas nécessairement optimale, mais elle est obtenue rapidement.
-
L’algorithme du plus proche voisin, qui peut lui aussi être considéré comme un algorithme glouton, est également simple. La première étape repose sur le choix aléatoire d’une première ville, et les étapes suivantes consistent à se déplacer de ville en ville en appliquant la règle du plus proche voisin, c’est-à-dire en sélectionnant la prochaine ville telle que le poids entre la ville courante et la prochaine ville soit minimal, et ce, jusqu’à avoir visité toutes les villes. Il faut enfin revenir à la première ville choisie, pour obtenir un cycle.
-
La méthode de l’élastique n’est pas facile à mettre en œuvre, mais l’idée reste simple. Comme son nom l’indique, elle repose sur un élastique dont la propriété est de s’étirer tout en gardant une force l’empêchant de se détendre. Pour comprendre le principe, il suffit d’imaginer que les villes sont des points fixes distants les uns des autres en fonction des poids. Il s’agit de placer un élastique au milieu des villes et d’étirer celui-ci jusqu’à ce qu’il passe par tous ces points fixes, tout en essayant de le détendre le moins possible.
-
L’algorithme de descente locale donne aussi rapidement de bons résultats. Son principe est le suivant : après la construction d’une solution initiale par l’utilisation d’un algorithme glouton, un opérateur de voisinage est appliqué à cette solution pour obtenir plusieurs nouvelles solutions voisines. Cet opérateur de voisinage consiste à modifier une solution selon une règle bien définie. Parmi cet ensemble de nouvelles solutions, l’algorithme va choisir la meilleure, celle qui a le cycle de plus petite longueur. Enfin, soit cette solution sélectionnée est meilleure que la précédente, et l’algorithme recommence à appliquer l’opérateur de voisinage sur cette nouvelle solution sélectionnée, soit la solution est moins bonne que la précédente et l’algorithme se termine. Il existe de nombreux opérateurs de voisinage d’efficacités variées. Un exemple simple est l’échange de deux villes dans le cycle. Pour obtenir l’ensemble de nouvelles solutions à partir d’une solution, il suffit de tester l’échange de chaque ville avec toutes les autres dans le cycle. Par exemple, avec une solution 1-2-3-4, en appliquant cet opérateur de voisinage, les solutions testées seraient : 2-1-3-4 (permuter 1 et 2), 3-2-1-4 (permuter 1 et 3), 4-2-3-1 (permuter 1 et 4), 1-3-2-4 (permuter 2 et 3), 1-4-3-2 (permuter 2 et 4), et 1-2-4-3 (permuter 3 et 4).
-
L’algorithme du recuit simulé, inspiré du processus de refroidissement et réchauffement d’un métal pour minimiser son énergie, peut être utilisé pour améliorer l’algorithme de descente locale. En effet, ce dernier algorithme se termine assez rapidement, puisqu’il n’autorise à explorer que les solutions améliorant les précédentes. Dans l’algorithme du recuit simulé, l’exploration de solutions autorise à explorer les solutions de moins bonne qualité. Au lieu de s’arrêter dès que la solution ne peut plus être améliorée par l’opérateur de voisinage, le recuit simulé continue l’exploration en prenant la meilleure solution parmi l’ensemble calculé, même si celle-ci est moins bonne que la solution précédente. Le critère d’arrêt est donc différent, il va dépendre du temps et de la dégradation de la solution, évaluée comme la différence de la longueur du cycle de la solution précédente et de la nouvelle solution sélectionnée. À chaque dégradation, l’algorithme s’arrête avec une probabilité dépendant de cette dégradation — plus la dégradation est grande, plus la probabilité de continuer diminue — et du temps ou du nombre d’itérations de l’algorithme — plus ce nombre est grand, plus la probabilité de continuer diminue elle aussi.
-
La recherche tabou, très utilisée pour de nombreux problèmes, est encore une amélioration de la descente locale. Elle converge vite vers une bonne solution. Le principe est similaire : à partir d’une solution, appelée solution courante, l’algorithme explore d’autres solutions en appliquant un opérateur de voisinage. La sélection d’une solution à partir de la solution courante doit être la meilleure parmi son voisinage. À chaque choix d’une solution parmi un voisinage, la solution choisie est stockée dans une liste tabou. Cette liste contient donc un certain nombre de solutions choisies précédemment. Le temps que la solution reste dans la liste dépend de la longueur maximale de cette liste, que l’on aura fixée au préalable. À chaque sélection, la nouvelle solution choisie ne doit pas appartenir à cette liste tabou. Contrairement à une simple descente locale, la solution sélectionnée peut être de moins bonne qualité que la solution courante, ce qui permet d’éviter d’être rapidement bloqué sur une solution et de continuer à en explorer d’autres. Après un certain nombre d’itérations, la meilleure solution trouvée, parmi toutes celles qui ont été explorées, est retournée par l’algorithme. Le nombre d’itérations maximal doit lui aussi être défini préalablement.
-
Il existe encore de nombreuses améliorations des algorithmes présentés ici, ainsi que des hybridations (mélanges d’algorithmes) proposées dans le but de rendre leur résolution plus performante.
Enfin, il existe d’autres méthodes approchées, fondées sur des principes totalement différents. Nous évoquerons deux d’entre elles, assez innovantes et intéressantes puisqu’elles s’inspirent de phénomènes naturels : les algorithmes génétiques et les algorithmes de colonies de fourmis.
Algorithme génétique
Les premiers algorithmes génétiques ont fait leur apparition vers les années 1970. L’idée d’un algorithme génétique est tirée de la théorie darwinienne de l’évolution. Chaque groupe d’individus (animaux, espèces végétales…), appelé aussi population, donne lieu à une génération suivante par reproduction sexuelle. Cette génération consiste à croiser les individus entre eux pour donner des descendants possédant les caractères des deux parents. En plus de ce croisement, des mutations de caractères interviennent aléatoirement dans la génération de la population suivante. Puis, cette nouvelle population subit une sélection, métaphore de la sélection naturelle : seuls les individus les mieux adaptés à l’environnement survivent. Enfin, à son tour, cette population donnera lieu par le même processus à une nouvelle population, qui sera encore plus performante dans son environnement. Pour développer un algorithme génétique, les individus sont des solutions, la sélection se fait grâce à leur qualité (évaluée à travers la fonction objectif), les croisements entre deux solutions sont faits à l’aide d’opérateurs de croisement, etc. Pour en savoir plus sur ces algorithmes, vous pouvez écouter le podcast Quand des algorithmes s’inspirent de la théorie de l’évolution… Nous allons décrire un tel algorithme pour le problème du voyageur de commerce.
Dans un premier temps, il faut initialiser une population, c’est-à-dire construire un nombre important d’individus, chaque individu correspondant à une solution. La première étape consiste donc à définir le codage d’un individu : comment l’individu peut représenter une solution. Pour cela, il existe deux types de codages : direct et indirect. Pour le codage direct, l’individu représente directement la solution du problème à résoudre. Par exemple, dans notre cas, un individu peut être représenté par la liste ordonnée de numéros des villes à visiter. C’est ce codage que nous utiliserons. Par contre, dans le codage indirect, l’individu n’exprime pas directement la solution, mais plutôt une manière de construire cette solution.
Pour initialiser une population, on peut lancer plusieurs fois un algorithme glouton, avec des paramètres différents pour obtenir des solutions différentes. Puis, pendant un certain nombre d’itérations, les étapes suivantes sont exécutées :
-
Tout d’abord, chaque individu est évalué. Pour cela, on calcule la valeur de la fonction objectif, c’est-à-dire la longueur du cycle parcouru par le voyageur de commerce.
-
Puis, une étape de sélection est appliquée. Cette étape permet d’éliminer les moins bons individus et de garder uniquement les meilleurs en fonction de leur évaluation. Il existe plusieurs méthodes de sélection. Une sélection par rang ne fait pas intervenir le hasard, contrairement à la roulette, car elle choisit les n meilleurs individus de la population. Chaque individu a ainsi une probabilité de sélection dépendant de son évaluation, avec une plus forte probabilité pour les meilleurs individus.
-
L’étape suivante consiste à croiser les individus précédemment sélectionnés pour obtenir une nouvelle population. Deux parents sont donc choisis pour appliquer un opérateur de croisement afin d’obtenir un descendant (nouvel individu). Il existe de nombreuses techniques de croisement ; dans le cas présent, nous utiliserons le « crossover en un point ». Cet opérateur consiste à recopier une partie du parent 1 et une partie du parent 2 pour obtenir un nouvel individu. Le point de séparation des parents est appelé point de croisement. Il faut cependant faire attention à ne pas visiter plusieurs fois la même ville (on ne recopie pas les villes déjà visitées), et à ne pas oublier de ville (on rajoute à la fin les villes non prises en compte). Voici un exemple avec 8 villes et un point de croisement juste après la troisième ville :
| Parent 1 | Parent 2 | Descendant |
| 1 | 2 | 1 |
| 2 | 6 | 2 |
| 3 | 1 | 3 |
|
|
||
| 4 | 8 | 8 |
| 5 | 4 | 4 |
| 6 | 3 | 5 |
| 7 | 5 | 7 |
| 8 | 7 | 6 |
-
Enfin, avant de revenir à la première étape, un procédé de mutation est utilisé pour diversifier les solutions au fur et à mesure des générations. Cette mutation consiste à modifier aléatoirement une petite partie d’un caractère dans certains individus de la nouvelle génération. Cette étape est effectuée avec une très faible probabilité, et consiste par exemple à échanger deux villes consécutives dans un individu.
Dans certains cas, après chaque croisement et mutation, une étape d’optimisation des descendants est appliquée. L’utilisation d’un algorithme de type recherche locale est adapté pour effectuer cette optimisation rapidement. Nous parlerons alors d’algorithme mimétique.
Ce type d’algorithme est intéressant pour obtenir plusieurs solutions de bonne qualité. En effet, à la fin de l’algorithme, la population est constituée des meilleures solutions trouvées.
Algorithme de colonies de fourmis
Les algorithmes s’inspirant des colonies de fourmis sont assez récents dans le domaine de l’optimisation. Ils ne sont pas encore en mesure de rivaliser avec les meilleurs algorithmes classiques, mais leurs résultats ont vite progressé. Nous présentons ici le principe d’un algorithme de fourmis appliqué à notre problème de voyageur de commerce, mais sans entrer dans les détails. Pour en savoir plus sur cette méthode, consultez le document L’intelligence en essaim. Vous y trouverez une applet qui montre le principe sous-jacent au choix du plus court chemin par les fourmis et une autre qui illustre son application au problème du voyageur de commerce.
Le principe de l’algorithme s’appuie sur l’aptitude des fourmis à éviter les obstacles et à toujours trouver un plus court chemin entre deux points. Lorsque plusieurs fourmis effectuent des allers-retours entre deux points A et B, pour rapporter de la nourriture par exemple, elles se mettent au fur et à mesure à emprunter le plus court chemin entre A et B. Ce phénomène est dû aux phéromones que chaque fourmi sécrète. En effet, chaque fourmi dépose une certaine quantité de phéromones sur le chemin qu’elle emprunte. Et une fourmi a tendance à choisir le chemin qui possède la plus grande quantité de phéromones. Un autre facteur est à prendre en compte : l’atténuation, qui exprime le fait que la quantité de phéromones sur chaque arête diminue dans le temps.
Voici un exemple schématique avec deux chemins possibles entre A et B, évitant un obstacle :
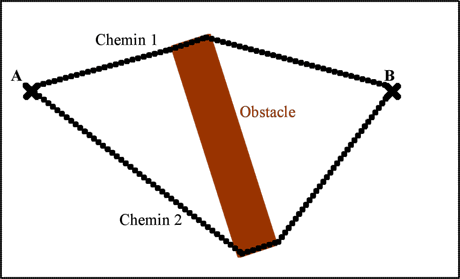
Comme le chemin 1 est plus court que le chemin 2, une fourmi qui emprunte le chemin 1 fera plus d’allers-retours en un même temps qu’une fourmi empruntant le chemin 2. Elle laissera donc plus de phéromones sur le chemin 1 que l’autre fourmi sur le chemin 2. Ainsi, les autres fourmis emprunteront plus souvent le chemin 1 que le chemin 2, et laisseront encore plus de phéromones sur le chemin 1. La différence sera renforcée à cause de l’atténuation. À terme, les fourmis tendront à ne passer que par le chemin 1.
Ce principe peut être repris pour le problème du voyageur de commerce. Il suffit de simuler un certain nombre de fourmis et leurs déplacements dans le graphe. Il faut imposer un sommet de départ qui sera aussi celui du retour pour toutes les fourmis, et les contraindre à passer par tous les sommets. Chaque fourmi laissera à son passage sur chaque arête une quantité de phéromones dépendant du poids de l’arête (plus le poids est petit, plus la quantité de phéromones laissée par la fourmi sera forte). Lorsqu’une fourmi se trouve à un sommet, elle partira vers un sommet qu’elle n’a pas encore visité avec une probabilité d’autant plus élevée que l’arête qui les relie possède le plus grand taux de phéromones. Les différents paramètres (nombre de fourmis, taux de phéromones, atténuation) peuvent être ajustés pour améliorer l’efficacité de l’algorithme.
Conclusion
Le problème du voyageur de commerce est toujours d’actualité dans la recherche en informatique, étant donné le nombre important de problèmes réels auxquels il correspond. Les problèmes dérivés et les extensions en sont très nombreux. Par exemple, des fenêtres de temps peuvent y être ajoutées. Ce concept consiste à imposer des contraintes de temps pour la traversée de chaque sommet. Autre exemple, il peut y avoir plusieurs voyageurs de commerce partant d’un même sommet, ou de sommets différents. Il suffit alors de considérer que les voyageurs de commerce sont des véhicules pour arriver à des problèmes de tournées de véhicules : étant donnée une flotte de véhicules, le problème consiste à déterminer les trajets de chacun pour livrer à moindre coût des clients en marchandise (chaque client est représenté par un sommet dans le graphe). Le nombre de véhicules peut être fixe ou non, les capacités des véhicules peuvent être les mêmes ou non, des fenêtres de temps peuvent être définies… Pour chacune de ces variantes, de nouvelles méthodes peuvent être explorées.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Yannick Kergosien
Maître de conférences à l'Université de Tours (Laboratoire d'informatique) et à l'École Polytechnique de l'Université de Tours.

Jean-Charles Billaut
Professeur à l'Université de Tours, directeur du Laboratoire d'informatique et enseignant à l'École Polytechnique de l'Université de Tours, ancien président de l'association ROADEF.