Les mathématiques financières des quants

Si le cinéma s’est depuis longtemps approprié l’univers de Wall Street et la figure du trader achetant ou vendant des actions frénétiquement, image fantasmée et très souvent éloignée de la réalité, l’actualité financière est de plus en plus occupée par les produits dérivés. Futures (contrats à terme), stock options, swaps, dérivés de crédit, CDOs, etc., en sont tous des exemples. De façon générale, les produits dérivés sont des contrats prévoyant un paiement à une date ultérieure d’un montant calculé à partir du prix à cette date d’un autre produit. Ils servent à se protéger contre des risques financiers ciblés et donc par symétrie, permettent aussi de s’y exposer.

Dans les banques d’investissement, qui en sont les principaux émetteurs, l’analyse des risques associés à ces produits dérivés est assurée par les quants, abréviation de l’anglais quantitative analysts. Parfois décrits comme « magiciens » ou « sorciers » par ceux ayant une connaissance limitée du domaine (ce qui n’est pas entièrement sans rappeler la façon dont des peuples anciens attribuaient à des dieux les phénomènes naturels incompréhensibles à l’époque : foudre, tremblements de terre, etc.), les quants sont les ingénieurs de la finance. D’une formation à forte composante mathématique (mathématiciens, physiciens, informaticiens…), leur rôle est de comprendre comment gérer ces produits dérivés. Il existe aussi, dans les fonds d’investissement notamment, des quants impliqués dans l’analyse statistique des historiques de prix à des fins d’investissement, mais il s’agit d’une activité très différente. Dans le cas présent, nous allons voir, en suivant un exemple, ce que font les « quants pour les produits dérivés ».

Les produits dérivés

Les produits dérivés sont des contrats entre deux parties qui prévoient un échange d’argent dont le montant dépend du prix d’autres actifs ou produits financiers, souvent à la date d’expiration du contrat. Ce montant est donc inconnu aujourd’hui. Ces autres actifs peuvent être de nature financière diverse : actions dans des entreprises, devises étrangères, matières premières, etc.. Dans le cadre d’un produit dérivé, ces actifs sont qualifiés de sous-jacents. Et le produit dérivé, justement, dérive de ces actifs.

Les produits dérivés, pour les plus simples d’entre eux en tout cas, ne sont pas d’invention nouvelle. Par exemple, vers 1710 au Japon commencent à s’échanger de façon standardisée les premiers contrats à termes (des futures) : ces contrats sont des promesses d’achat ou de vente d’un certain bien, à une date ultérieure et à un prix convenu le jour de la transaction. Ils sont donc non-optionnels. Cependant, les produits dérivés ont réellement pris leur essor dans les années soixante-dix.

Les produits dérivés les plus connus aujourd’hui sont probablement les options. La terminologie financière se rattache ici très bien à l’usage commun de « mettre une option sur quelque chose ». Pour une option d’achat par exemple, à la date prévue d’expiration du contrat, le détenteur du contrat a la possibilité d’acheter auprès de l’émetteur l’actif sous-jacent à un prix convenu à l’avance, s’il le souhaite. Bien entendu, ce droit ne sera utilisé que si le prix convenu est plus avantageux que le prix sur le marché.

Prenons l’exemple d’une compagnie de distribution de gaz qui aurait promis à ses clients des tarifs fixes. Cette compagnie doit cependant se procurer ce gaz tous les mois en l’achetant sur des marchés où le prix peut varier. Si le prix du gaz augmente trop, ne pouvant modifier ses tarifs à la vente, la compagnie risque d’enregistrer des pertes, voire de faire faillite si celles-ci sont trop importantes. Pour se protéger contre des hausses de prix, elle peut acquérir, auprès d’une banque en général, l’option d’acheter le gaz dont elle aura besoin le mois prochain à un prix fixé aujourd’hui et qui lui convient. Le mois prochain, si le gaz a trop augmenté, la compagnie fait valoir son option et achète alors son gaz auprès de la banque, pour moins cher que le prix du marché. Si au contraire le gaz a baissé, elle n’utilise pas son option et se fournit directement sur le marché.

La problématique initiale

Plaçons-nous à présent du point de vue de la banque auprès de qui la compagnie de distribution de gaz achète une option sur le gaz dont elle aura besoin le mois prochain. Se pose alors une première question : à combien vendre une telle option ?

En effet, la banque récupère ici la « patate chaude » : le risque de pertes financières associé à une hausse des prix du gaz sur le marché est transféré de la compagnie vers la banque. Admettons que la compagnie ait acheté son gaz pour 100 Gils ce mois-ci (prix arbitraire dans une monnaie fictive, simplement pour fixer les idées), et qu’elle achète une option pour pouvoir l’acquérir à ce même prix le mois suivant. Si le prix de la même quantité de gaz passe, disons, à 120 Gils alors, en théorie, la banque devrait acheter ce gaz à 120 Gils sur le marché pour le vendre à 100 Gils à la compagnie, et c’est donc la banque qui encaisse les pertes qui auraient autrement été celles de la compagnie. Si le prix baisse à moins de 100 Gils, alors la compagnie achètera le gaz sur le marché. Dans la pratique, le contrat prévoit simplement un règlement en espèces : si le gaz augmente, la banque paiera la différence à la compagnie (prix du marché moins prix convenu dans l’option), tandis que dans le cas contraire, elle ne paiera rien. Le schéma ci-dessous décrit le montant du paiement effectué par la banque à la compagnie dans cet exemple, à la date d’expiration de l’option.

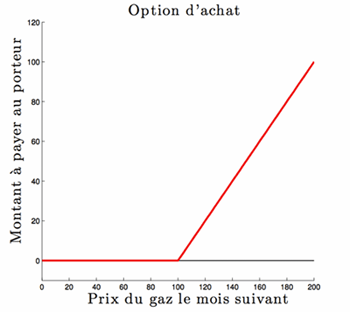
L’option pouvant donc être vue comme une assurance, il se pose la question de savoir quelle prime facturer.

On peut aussi remarquer que le paiement effectué par la banque à la compagnie sera toujours positif : soit nul, soit strictement positif. Mais son montant est inconnu aujourd’hui. La question est de savoir quel paiement la compagnie devrait faire à la banque aujourd’hui pour recevoir cette somme inconnue dans un mois. C’est ce problème auquel les quants ont pour fonction de répondre.

La solution dans un modèle simple

Supposons d’abord que, pour diverses raisons, le gaz requis par la compagnie dans un mois ne puisse coûter que 80 Gils si le prix a baissé, ou 120 Gils si le prix a augmenté. Les scénarios possibles sont donc représentés par le schéma suivant :

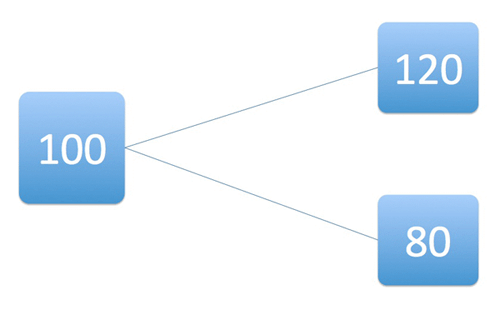
Imaginons ensuite qu’un trader de la banque vende à la compagnie cette option d’acheter le gaz pour 100 Gils. Voici la solution proposée par les quants. Il va la vendre pour 10 Gils. Mais, au lieu de simplement espérer que les prix baissent, il va investir 50 Gils dans le gaz. Pour cela il va emprunter 40 Gils auprès de sa banque, ou sur les marchés, peu importe : chaque trader a sa comptabilité propre et celui de notre exemple a maintenant une position de -40 Gils en « espèces », avec un demi-volume de gaz d’une valeur de +50 Gils. À la date d’expiration de l’option, dans un mois, il va revendre son investissement en gaz et utiliser les Gils ainsi récupérés pour rembourser son emprunt de 40 Gils. En suivant ces instructions, le nombre de Gils qui lui reste correspond alors exactement au montant qu’il doit à la compagnie de gaz, quel que soit ce montant.

Sans chercher à expliquer comment obtenir cette solution — les lecteurs intéressés pourront se référer à l’encadré expliquant comment déterminer le prix de l’option — vérifions qu’elle fonctionne bien. Si le prix du volume de gaz requis est passé de 100 à 80 Gils, il s’agit d’une baisse des prix de 20 %. Le demi-volume que le trader possède a donc perdu 20 % de sa valeur initiale, soit 50 Gils, et vaut maintenant 40 Gils. Le trader revend ce demi-volume pour 40 Gils, rembourse son emprunt de 40 Gils et se retrouve donc avec 0 Gil. C’est exactement le montant que la banque paie à la compagnie dans ce scénario. Si le prix du volume de gaz requis est passé de 100 à 120 Gils, il s’agit d’une hausse des prix de 20 %. Le demi-volume que le trader possède a donc gagné 20 % de sa valeur initiale, soit 50 Gils, et vaut maintenant 60 Gils. Le trader revend ce demi-volume pour 60 Gils, rembourse son emprunt de 40 Gils et se retrouve donc avec 20 Gils. C’est exactement le montant que la banque paie à la compagnie dans ce scénario. En effet, la compagnie reçoit en paiement la différence entre le prix du marché et le prix convenu dans l’option, soit 120 – 100 = 20 Gils.

Dans cet exemple, le trader impliqué dans cette transaction part de 0 Gil. Il vend l’option au prix judicieux de 10 Gils, et investit judicieusement dans le gaz. À la fin du mois, il liquide son investissement, paie la compagnie, et se retrouve avec 0 Gil, et ce, quel que soit le scénario qui s’est réalisé ! S’il n’avait rien fait, et à supposer qu’il vende toujours l’option pour 10 Gils, il aurait pu se retrouver avec -10 Gils (cas d’une augmentation des prix, et donc un paiement de 20 Gils à la compagnie), ou +10 Gils (cas d’une baisse des prix, et donc un paiement de 0 Gil à la compagnie). Il se serait agi d’un pari, et comporterait des risques. La solution du quant permet à la banque d’annuler complètement le risque hérité en vendant l’option.

L’idée de réplication

Cet exemple met en œuvre l’idée centrale de réplication. Du côté de la compagnie de gaz, il y a une option, dont on cherche à déterminer le prix : acheter cette option est un investissement qui rapporte 0 ou 20 Gils suivant le scénario qui se réalise. Du côté du trader, dans le modèle utilisé, il y a initialement une richesse de 10 Gils, sous la forme d’un investissement judicieux fait de 40 Gils de découvert en espèces et de 50 Gils dans le gaz. Cet investissement rapporte exactement les mêmes sommes que l’option dans exactement les mêmes scénarios. Autrement dit, il réplique l’option. Cet investissement judicieux des 10 Gils n’est pas l’option, mais il rapporte exactement la même chose dans les mêmes cas. Les 10 Gils sont le capital requis pour répliquer — on dit parfois aussi synthétiser — l’option à l’aide uniquement de moyens plus simples (un compte en Gils et un investissement dans le marché). Les financiers parlent de prix juste ou de valeur fondamentale de l’option.

Imaginons une boulangerie qui veut vendre des sandwichs. D’une part, il faut savoir produire un sandwich, à partir de produits plus simples (pain, salade, etc.) et en suivant une certaine recette (couper le pain d’abord, puis mettre la salade dans le pain, etc.). D’autre part, il faut décider du prix auquel vendre le sandwich. La somme des prix des ingrédients permettant de faire le sandwich donne la valeur fondamentale. Beaucoup d’autres facteurs entrent en jeu dans le prix auquel la boulangerie décidera de proposer le sandwich, mais la valeur fondamentale est clairement une information à prendre en compte dans la décision finale. De façon similaire, les quants cherchent à évaluer le prix juste des produits dérivés (le prix des ingrédients) et la stratégie (la recette à suivre) permettant de reproduire le paiement d’un produit dérivé à partir de produits financiers plus simples. Il y a cependant une différence : les sandwichs sont des matériels et doivent être fabriqués avant d’être vendus. Les contrats dérivés quant à eux sont immatériels et peuvent toujours être conclus, c’est à dire vendus. De plus, les termes disant comment calculer le paiement ne sont limités que par l’imagination. Mais le principe reste fondamentalement le même que celui de la fabrication physique, et c’est en ce sens qu’on parle d’ingénierie financière.

Cette idée de réplication était comprise à l’origine dans un article des économistes Black et Scholes de 1973. Avant cela, on pensait que le prix des options devait se déterminer en ayant une vue sur le marché (« si je pense que le prix va monter, je devrais sûrement vendre l’option plus cher »). Les options étaient des produits peu compris, donc risqués, et relativement peu courants. Par la suite, le marché des options s’est énormément développé, passant de presque rien dans les années soixante-dix à une activité impliquant des milliers de milliards de dollars aujourd’hui. Les acteurs s’échangeant aujourd’hui des options d’achat sur le gaz, par exemple, sont des entités ayant un risque à couvrir, des entités prêtes à couvrir de tels risques, ou simplement des investisseurs ayant une vue sur le marché et espérant des profits.

Un modèle un peu plus réaliste

Il faut noter que la solution proposée dépend du modèle, c’est-à-dire de l’ensemble de scénarios envisagés. Et l’on peut objecter que la possibilité que le prix ne change pas n’a pas été prise en compte dans le modèle précédent. En ajoutant ce scénario, le modèle est maintenant décrit par le schéma suivant.

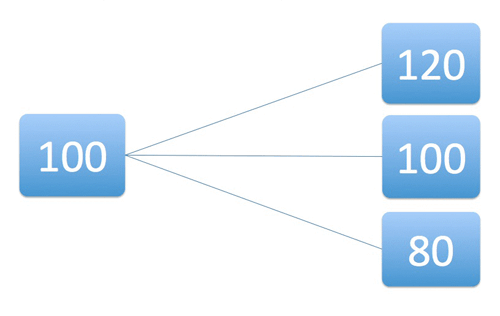
Dans ce modèle, il n’est pas possible de répliquer l’option dès le départ, comme précédemment (cela tient essentiellement au fait qu’il y ait maintenant trois scénarios et seulement deux variables d’ajustement pour la banque : le prix de l’option et l’investissement initial en gaz). Cependant, quitte à considérer que le trader peut investir dans le gaz aujourd’hui, au lieu de simplement vendre l’option et attendre, on peut considérer que le trader peut aussi ajuster son investissement dans quinze jours. Considérons donc le modèle suivant, avec quatre scénarios.

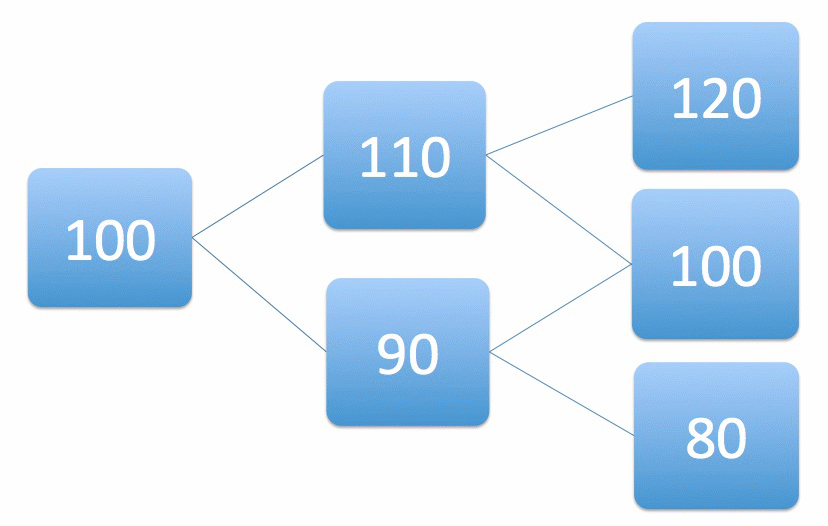
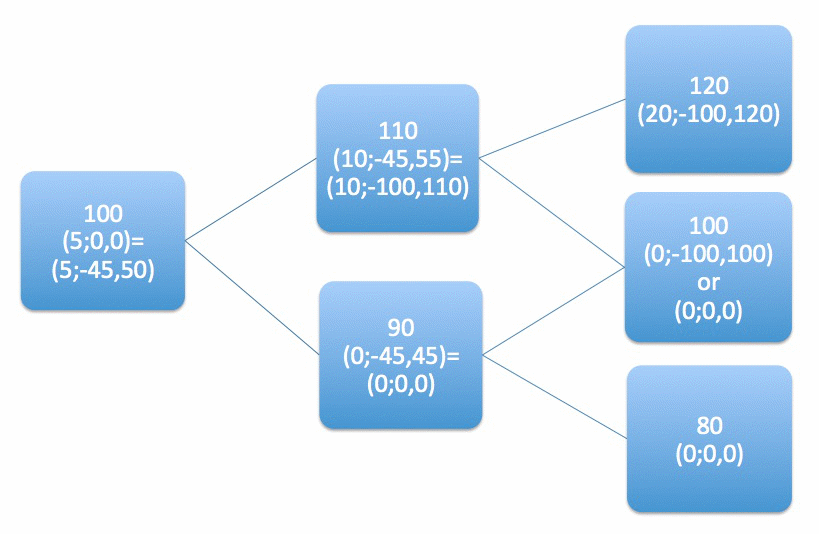
Dans ce modèle, il est possible de répliquer l’option. La solution du quant prend alors la forme de l’algorithme suivant.
– Prix à demander pour l’option : 5 Gils
– Initialement, investir dans un demi-volume de gaz (valant 50 Gils, donc emprunter 45 Gils)
– 15 jours plus tard :
* si le prix est monté à 110 Gils : acheter un demi-volume de gaz supplémentaire.
* si le prix est descendu à 90 Gils : vendre le demi-volume de gaz possédé.

Le schéma ci-dessous montre l’évolution de la position du trader, après application de la recette ci-dessus. Sous le prix du gaz, entre parenthèses, est indiquée la valeur totale de la position du trader, décomposée en d’une part le nombre de Gils sur son compte et d’autre part la valeur en Gils de son investissement en gaz. Par exemple (5 ; -45, 50) signifie que le trader a une position valant 5 Gils, faite de 45 Gils de découvert sur son compte et d’un investissement dans le gaz valant 50 Gils.

Des modèles encore plus réalistes

Bien sûr, le modèle précédent est encore bien trop peu réaliste. Il n’y a aucune raison de croire que le prix dans un mois ne peut prendre que trois valeurs, et qu’il n’y a que quatre scénarios possibles. On peut considérer des modèles avec de plus en plus de scénarios et prendre en compte la possibilité pour le trader d’ajuster sa position plus fréquemment, au fur et à mesure des mouvements des prix. Ci-dessous sont représentés 3 modèles avec, respectivement, 8, 16 et 32 scénarios. Ils sont suivis d’un modèle où le trader peut ajuster sa position une fois par jour (pour un mois de 31 jours). Pour ce dernier, on ne représente que quelques scénarios possibles, pour des raisons de lisibilité du schéma (il y a en effet 2³⁰ scénarios possibles, soit un peu plus d’un milliard).

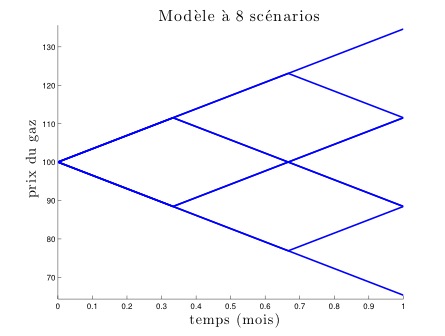
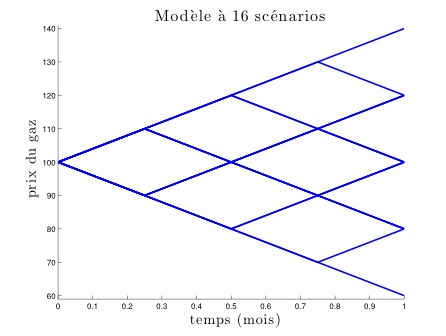
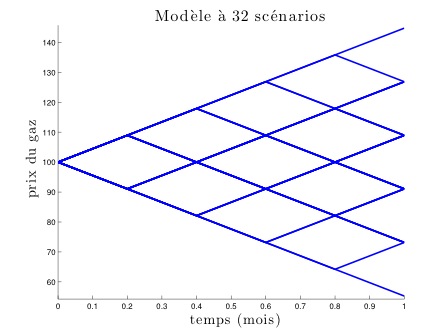
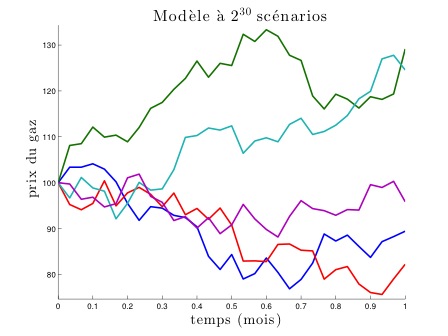
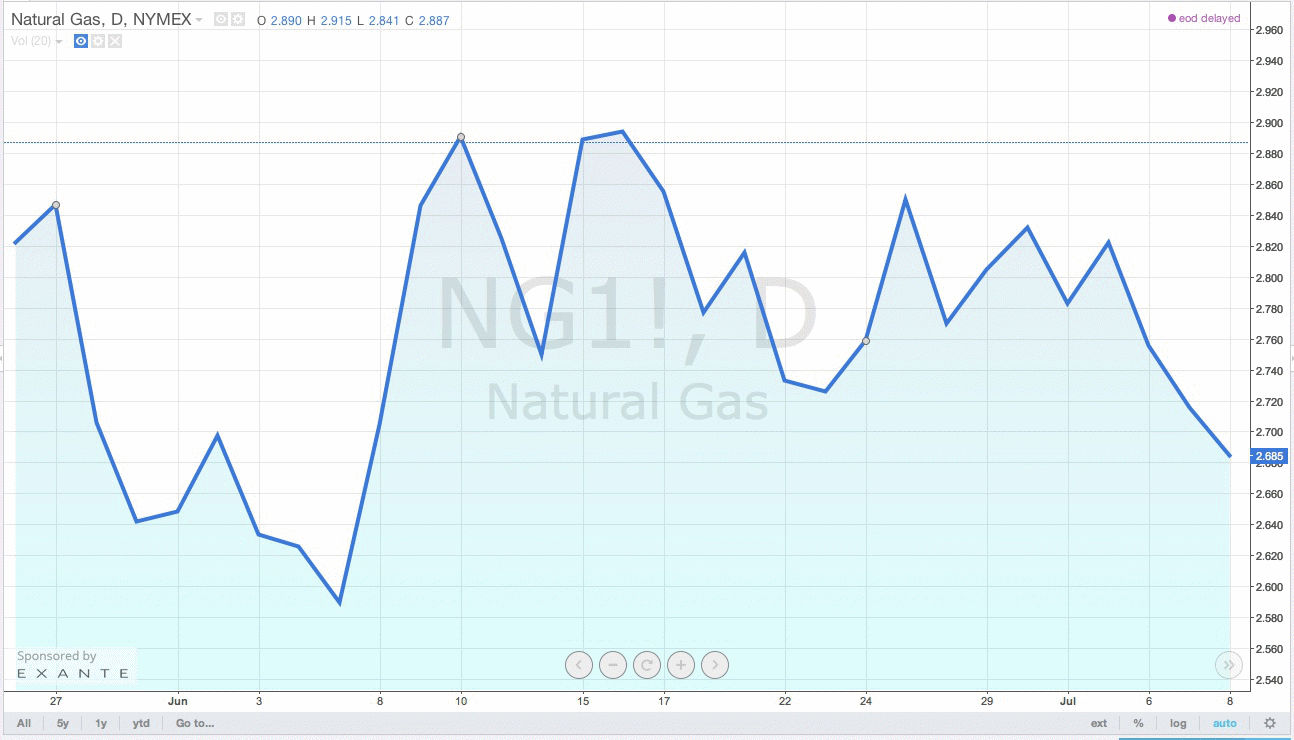
En continuant à affiner cette suite de modèles, on obtient à la limite un modèle où les prix évoluent continûment dans le temps et peuvent prendre un continuum de valeurs. Plus précisément, on obtient ici un mouvement brownien (du nom du botaniste britannique Robert Brown qui observa en 1827 le mouvement erratique de particules de pollen dans un bol d’eau, mouvement qui peut être décrit par ce modèle). C’est un cas particulier de modèle de prix de Bachelier (du nom du mathématicien français Louis Bachelier, considéré comme l’un des précurseurs de l’utilisation des mathématiques en finance par ses travaux en 1900). D’autres modèles de prix sont possibles, le plus célèbre étant sûrement celui utilisé initialement par les économistes américains Black et Scholes, qui sert un peu de modèle de référence. Ci-dessous sont représentés, pour une évolution sur un mois, quelques scénarios dans chacun de ces modèles parmi l’infinité des scénarios envisagés par chaque modèle, ainsi que l’évolution du prix du gaz en juin 2015, autrement dit le scénario qui s’est réalisé ce mois-là.

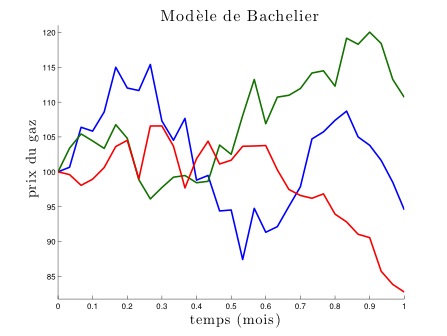
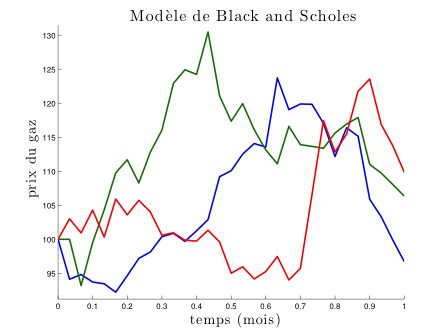
Dans ces modèles ayant une infinité de scénarios, la détermination de la valeur fondamentale d’un produit dérivé et de la stratégie d’investissement dans des produits simples pour le répliquer implique la résolution d’un type d’équation différent du système linéaire utilisé dans les premiers modèles (voir encadré plus haut) : il s’agit d’une équation aux dérivées partielles. Dans le cas du modèle de Black et Scholes, et pour une option d’achat, la solution est donnée par la formule de Black et Scholes. Pour d’autres produits dérivés, et d’autres modèles, on ne sait en général pas calculer la solution exacte d’une telle équation. C’est-à-dire qu’on ne sait pas donner de formule exprimant explicitement la solution en fonction des paramètres du modèle et du produit dérivé. En pratique cependant, on n’a pas vraiment besoin de la formule : ce qui compte pour le trader c’est de savoir le prix fondamental du produit dérivé, et quels produits simples il doit acheter à un moment donné. On a donc recours à des algorithmes de résolution numérique. Ce sont des procédures de calcul qui fournissent une valeur approchée de la solution. Par exemple, on peut calculer le prix à un centime près, ou à un millième de centime près. Et plus on calcule longtemps, plus on obtient un résultat précis. Ces calculs seraient très longs et rébarbatifs à faire à la main, et sont donc programmés par les quants pour être réalisés par un ordinateur (rappelons qu’ordinateur se dit computer en anglais, ce qui se traduit littéralement par calculateur : ce sont des machines qui ont été inventées précisément pour faire des calculs !).

En conclusion

Comme on a pu le constater dans l’exemple ci-dessus, le travail des quants est analytique et non prédictif. Il ne s’agit pas de dire comment va évoluer le marché, mais de dire comment répliquer un produit dérivé (c’est-à-dire imiter à partir de produits financiers plus simples l’investissement qu’il représente) et par là-même éliminer le risque associé, au fur et à mesure des mouvements du marché.

Les produits dérivés simples comme l’option d’achat présentée plus haut sont de fait tellement échangés (vendus, achetés, revendus, etc.) qu’il existe déjà un prix, le prix de marché, auquel on peut se les procurer ou les vendre. De la problématique initiale, ce n’est donc plus tellement la détermination du prix fondamental qui importe. Mais, d’une part, comprendre la réplication d’un produit dérivé permet l’évaluation des risques associés à la position d’un trader qui en aurait acheté ou vendu : « si demain le prix du gaz et d’autres paramètres du marché changent, comment évolue la valeur de ma position ? ». D’autre part, des produits toujours plus complexes et ciblés, souvent faits « sur mesure », se sont développés. Par exemple, un contrat peut permettre à la compagnie de distribution de gaz de recevoir la différence si le prix du gaz est monté à plus de 100 Gils (comme une option d’achat), mais ce paiement est limité à 50 Gils maximum, et le contrat est entièrement annulé si le prix a dépassé 200 Gils à un moment donné, tout en assurant à la compagnie un taux de change déterminé pour le mois prochain si la distribution de gaz se fait dans un pays utilisant une autre monnaie. Les produits dérivés simples comme les options d’achat peuvent alors servir à leur tour d’ingrédient de base pour répliquer ces produits plus complexes.

Comme il n’y a pas de prix de marché pour ces produits complexes, la détermination du prix fondamental importe donc de nouveau. Mais une fois celui-ci identifié, la banque voudra sûrement vendre le produit pour plus cher que le prix de revient, tirant des bénéfices de son expertise (tout le monde n’a pas des ingénieurs financiers à sa disposition) et éventuellement de sa position sur le marché (si aucune autre banque n’est prête à proposer à cette compagnie le même produit sur mesure, celui-ci sera probablement plus cher).

Pour finir, il faut souligner que si les modèles utilisés en pratique sont plus complexes et plus riches que les quelques-uns présentés ci-dessus, et requièrent des mathématiques plus avancées, ils ne sont pas pour autant toujours satisfaisants comme modèles d’évolution des prix. De la recherche continue à être faite, dans les banques comme dans le milieu universitaire, proposant de nouveaux modèles, cherchant les équations décrivant comment répliquer les nouveaux produits dérivés issus de l’imagination des financiers, et cherchant à résoudre numériquement ces équations.