Les maths de l’espace-temps qui décrivent et dépassent le cerveau

Les mathématiques qui décrivent l’espace-temps

La gravitation maintient les planètes en orbite autour du Soleil et fait tomber des objets au sol dans votre salon. Sa modélisation mathématique — c’est-à-dire sa mise en équation — est extrêmement importante. Les équations permettent en effet de faire des prédictions utiles : quelle sera la trajectoire exacte de cet astéroïde qui semble se rapprocher de la Terre ? Un bâtiment construit de cette façon va-t-il s’écrouler ?

La gravitation a été modélisée différemment au fil des années. Newton la représentait par une force : si une pomme qui se décroche d’un arbre tombe sur la Terre, c’est qu’il y a une force qui attire la pomme vers la Terre. Cette force s’applique sur des objets ayant une masse, et ne s’applique donc pas à la lumière qui elle n’en a pas. Autrement dit, avec le modèle de gravitation de Newton, la lumière devrait toujours se déplacer en ligne droite.

Plus tard, Einstein remet en question le modèle de Newton et propose de toutes nouvelles équations dans sa théorie de la Relativité Générale. Il décrit la gravitation comme l’effet de la déformation de l’espace-temps par la présence de masse comme une galaxie, montrée sur l’image ci-dessous. Cette distorsion modifie la trajectoire des objets, y compris celle de la lumière.

Einstein prédit donc que la lumière dévie en passant près d’un astre et contredit ainsi puissamment le modèle de Newton. En 1919, Eddington observe effectivement la déviation de la lumière d’étoiles à son passage proche du Soleil, lors de l’éclipse nommée ensuite « Éclipse de la Relativité Générale ». La modélisation d’Einstein l’emporte donc sur celle de Newton.

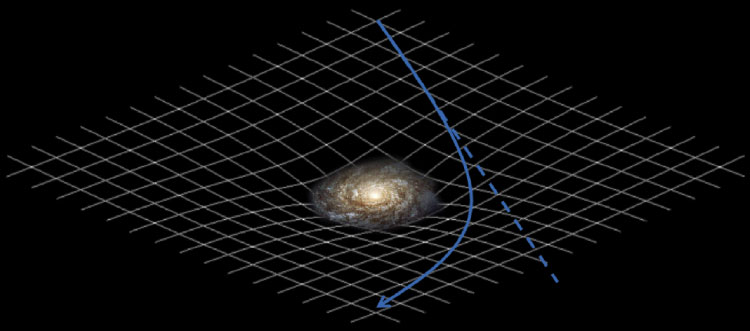
Image : Daniel Suchet, Lentilles gravitationnelles, 2014.

Les mathématiques sont un langage

Newton et Einstein ont donc tous les deux mis en équation la gravitation et la trajectoire de la lumière dans l’espace-temps. Mais Einstein a utilisé une théorie plus poussée : la géométrie riemannienne, une branche des mathématiques qui permet d’étudier la géométrie des espaces courbes comme celle de l’espace-temps.

Des mathématiques permettent donc de formuler la physique de l’espace-temps. Autrement dit, on se sert des mathématiques comme d’un langage très précis permettant de décrire des concepts complexes.

Un même langage peut s’utiliser pour décrire des expériences différentes : nous employons des mots de français pour raconter nos vacances à la plage ou pour décrire notre journée de travail. De façon similaire, une même théorie mathématique peut s’utiliser pour décrire plusieurs phénomènes, allant de la physique à la médecine.

En physique, la géométrie riemannienne met en équation la trajectoire courbe de la lumière dans l’espace-temps. En médecine, la trajectoire de l’information neuronale dans le cortex visuel est elle aussi courbe. Ceci est dû non pas à la présence de corps massifs dans notre cortex, mais à des raisons physiologiques. Il paraît donc logique d’utiliser la géométrie riemannienne pour mettre en équation la trajectoire de l’information neuronale dans le cortex visuel. Regardons de plus près.

Physiologie du cortex visuel

La vision est le procédé d’analyse des informations collectées par nos yeux. Dans ce but, une zone spécialisée de notre cerveau est mobilisée : le cortex visuel. Comment le cortex visuel nous permet-il de voir ?

Le cortex visuel primaire, nommé V1, est la porte d’entrée des informations visuelles dans notre cerveau. V1 est composé de neurones qui jouent le rôle de détecteurs : chaque neurone est sensible à l’intensité lumineuse d’un point particulier de notre champ visuel, ainsi qu’à l’orientation de la variation d’intensité en ce point.

Comment sont organisés les neurones dans V1 ? Deux neurones anatomiquement proches sont sensibles à des points proches de notre champ visuel. De plus, Hubel et Wiesel (Prix Nobel 1981) ont montré que les neurones détectant toutes les orientations d’intensité lumineuse pour un même point du champ visuel formaient une structure anatomique bien définie : une hypercolonne d’orientation.

Les neurones se transmettent des messages électrochimiques pour réaliser des opérations de perception visuelle. Prenez une photographie dont vous retirez quelques bandes, comme sur l’image ci-dessous. Certains neurones détectent de l’information visuelle et s’activent : il s’agit des neurones associés aux points qui montrent une partie de la photo. D’autres ne détectent rien : il s’agit des neurones associés aux bandes blanches.

Image : Ugo Boscain, Hypoelliptic diffusion and human vision: a semi-discrete new twist. Conférence au séminaire “Geometric Model in Vision” à l’Institut Poincaré, 2014.

Malgré l’information manquante, notre cerveau reconnaît ce qu’il y a sur la photo : on y voit un œil. En effet, les neurones qui ont détecté de l’information visuelle diffusent cette information aux neurones voisins. Autrement dit, ils indiquent à leurs voisins ce que ceux-ci sont censés voir. Le cerveau complète donc l’image.

Les mathématiques qui décrivent notre cortex visuel

Mais à quels voisins communiquent-ils ? Il n’y a qu’un neurone par hypercolonne d’orientation qui doit s’activer : il n’y a qu’une orientation de variation d’intensité associée à un point donné de l’image. Le neurone à activer est choisi de telle sorte que l‘image soit complétée continument : si l’intensité varie dans une direction donnée à un endroit donné, c’est qu’elle doit varier dans une direction semblable à un endroit proche. Cette logique est implémentée physiologiquement et l’activité neuronale suit une trajectoire courbe, d’hypercolonne à hypercolonne, dans le cortex. Pour en savoir plus, lire Jean Petitot, Neurogéométrie de la vision, 2008.

On peut mettre cette communication neuronale en équation avec la géométrie riemannienne, ces mathématiques qui ont conduit au succès de la théorie d’Einstein. En effet, la diffusion de l’information neuronale ressemble beaucoup à une diffusion de chaleur, mais dans un espace courbe !

Lorsque l’on allume un radiateur dans une pièce, la chaleur se diffuse dans toutes les directions en ligne droite. Lorsqu’un neurone « s’allume » car il a détecté de l’information visuelle, l’information se diffuse aux neurones qui lui sont connectés dans les hypercolonnes voisines… en trajectoires courbes. On adapte donc l’équation de diffusion de la chaleur à un espace courbe en l’exprimant avec la géométrie riemannienne.

Des mathématiques à l’informatique : un ordinateur qui voit comme l’homme

Pour vérifier ce modèle de la vision humaine, on l’a programmé dans un ordinateur. Les mathématiques sont un langage et l’informatique en est un autre. De la même façon que l’on peut traduire un texte du français à l’allemand, on peut traduire des équations mathématiques en langage informatique.

On a donc construit un cortex visuel virtuel en traduisant les formules mathématiques en un code informatique, c’est-à-dire en implémentant l’équation de diffusion riemannienne dans l’ordinateur pour propager l’intensité d’une image détériorée. L’ordinateur reconstitue alors l’image.

Image : Ugo Boscain, Hypoelliptic diffusion and human vision: a semi-discrete new twist. Conférence au séminaire “Geometric Model in Vision” à l’Institut Poincaré, 2014.

Autrement dit : l’ordinateur voit ! Une même théorie mathématique a permis de décrire avec succès deux processus complètement différents : l’espace-temps et la vision humaine.

Dépasser le cerveau :  un ordinateur qui voit mieux que l’homme

L’ordinateur réalise donc une opération de perception visuelle comme le ferait le cerveau humain. Mais peut-il dépasser notre cerveau en termes de vision ? Que se passe-t-il si l’on couple l’équation de diffusion neuronale avec des techniques de restauration déjà utilisées en vision par ordinateur ?

Cette modification peut se tester sur le cortex visuel implémenté dans l’ordinateur. Alors que notre cerveau ne reconnaît pas l’image suivante, l’ordinateur avec sa vision améliorée le peut facilement, puisqu’il reconstruit l’image.

Image : Ugo Boscain, Hypoelliptic diffusion and human vision: a semi-discrete new twist. Conférence au séminaire “Geometric Model in Vision” à l’Institut Poincaré, 2014.

On peut donc implémenter un cortex visuel virtuel plus puissant que celui de l’humain. On pourra même aller plus loin, et programmer un ordinateur qui verra et reconstruira des images en 3D, c’est-à-dire qui percevra et complètera des volumes et leur intérieur. Cela pourra servir en imagerie médicale : les scanners et IRMs produisent des images 3D de l’intérieur de notre corps. La reconstruction de ces images permettra d’augmenter leur résolution, et de se servir de ces images améliorées à des fins thérapeutiques.

Pour en savoir plus, lire Nina Miolane, Xavier Pennec, A survey of mathematical structures for extending 2D neurogeometry to 3D image processing, 2015.