
Les planètes tournent-elles rond ?
En quoi le calcul numérique précis de la position des planètes du système solaire sur des dizaines de millions d’années dans le passé est-il un enjeu scientifique important ? Il permet notamment de réaliser des échelles de datation géologique. En effet, la position des planètes et leurs paramètres orbitaux, comme l’inclinaison, influencent la manière dont les sédiments se déposent sur la surface de la Terre. L’observation de ces dépôts de sédiments permet donc de faire des datations géologiques.
Un tel calcul géologique est connu grâce aux travaux de l’astronome et mathématicien Jacques Laskar, de l’Observatoire de Paris, et de ses collègues. Le récent calcul nommé La2010, qui utilise des méthodes numériques géométriques, montre que la disparition des dinosaures (il y a environ 65 millions d’années), pourrait être légèrement plus ancienne qu’on ne le pensait.
1. Calculer les trajectoires
Mais faisons un saut dans le temps. Nous sommes le premier janvier de l’année 1600, Johannes Kepler s’installe à Prague pour devenir le nouvel assistant de l’astronome Tycho Brahe. Il doit en effet fuir précipitamment Graz pour échapper aux persécutions notamment causées par son adhésion à la théorie controversée de Copernic selon laquelle les planètes tournent autour du Soleil.
Mars : une planète qui ne tourne pas rond
Tycho Brahe s’intéresse beaucoup au mouvement des planètes et a déjà calculé très précisément les orbites de planètes connues. Mais la planète Mars échappe à la compréhension : impossible de prédire convenablement sa trajectoire. Sans le mettre en garde contre la difficulté, Brahe demande à Kepler de calculer l’orbite précise de Mars. Il faudra près de six années à Kepler pour achever ce travail.
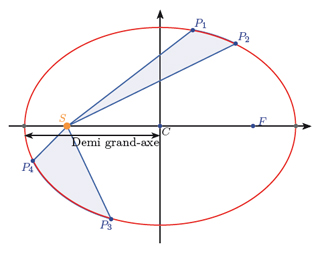
Illustration des lois de Kepler. \(S\) (le Soleil) et \(F\) sont les foyers de l’ellipse. Par la loi des aires, les domaines \(S P_1 P_2\) et \(S P_3 P_4\) ont la même aire. Le temps mis pour aller de \(P_1\) à \(P_2\) est égal à celui pour aller de \(P_3\) à \(P_4\).
En effet, alors que Vénus a une trajectoire presque circulaire, la trajectoire de Mars est plus complexe : c’est une ellipse, dont l’aplatissement, mesuré par l’excentricité, est le plus élevé de toutes les planètes du système solaire, après Mercure.
Ceci amène Kepler à proposer les trois lois fondamentales qui portent son nom :
- Les planètes décrivent des trajectoire elliptiques dont le Soleil est un foyer ;
- Le segment reliant le Soleil et la planète balaie des aires égales pendant des temps égaux ; cet invariant du problème est appelé la loi des aires ;
- Le carré de la période de rotation d’une planète (temps entre deux passages successifs devant une étoile lointaine) est proportionnel au cube du demi-grand axe de la trajectoire elliptique de la planète.
Une justification historique de la loi des aires par Newton
En 1684, Isaac Newton, s’appuyant sur les trois lois de Kepler, énonce la loi de gravitation universelle, selon laquelle tous les objets du cosmos s’attirent avec des forces de même valeur (mais de directions opposées), proportionnelles au produit de leurs masses et inversement proportionnelles au carré de la distance qui les sépare. Cette loi est utilisée pour calculer la position des planètes.
On peut formaliser la force gravitationnelle \(\overrightarrow{F}_{S\rightarrow P}\) exercée par le soleil S sur une planète P par la formule suivante, où G est la constante universelle de gravitation, mS, mP les masses des astres S et P, d la distance de S à P et \(\overrightarrow{u}\) un vecteur de longueur 1 dirigé de S vers P : \[\overrightarrow{F}_{S\rightarrow P}= -\overrightarrow{F}_{P\rightarrow S} = -\frac{G m_S m_P}{d^2}\overrightarrow{u}\]
À l’aide de ses travaux sur la gravitation, Isaac Newton donne, dans ses Principia Mathematica, une justification de la seconde loi de Kepler, en utilisant ce qui peut s’interpréter comme une méthode numérique géométrique (comme cela a été mis en évidence par E. Hairer, C. Lubich et G. Wanner, référence en fin d’article). Newton a en fait démontré une version discrète, et non continue, de la loi des aires, comme si le mouvement se faisait par à-coups successifs.
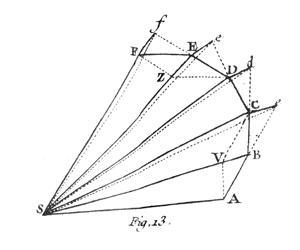
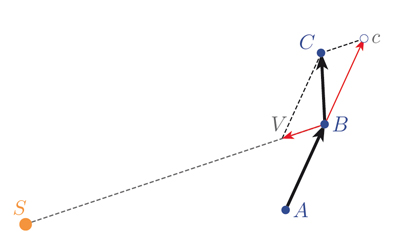
L’idée est la suivante : il s’agit de faire exercer la force d’attraction du Soleil non pas constamment au cours du temps, mais par impulsions. S représente le Soleil, et on suppose qu’une planète est située initialement au point A. Supposons pour l’instant que le Soleil n’exerce pas de force d’attraction. Dans ce cas, la planète se déplace de A vers B, de manière rectiligne, avec une vitesse constante dans la direction \(\overrightarrow{AB}\). La planète devrait continuer ainsi jusqu’en c avec \(\overrightarrow{AB}\) = \(\overrightarrow{Bc}\). Appliquons maintenant une « impulsion de force d’attraction » : cette force ajoute une composante de vitesse au mouvement de la planète que Newton représente par le vecteur \(\overrightarrow{BV}\) s’exerçant le long du segment SB. La vitesse de la planète possède alors deux composantes, le vecteur \(\overrightarrow{Bc}\) et le vecteur \(\overrightarrow{BV}\), dont le vecteur résultant est \(\overrightarrow{BC}\), ce qui définit le point C. La planète se déplace ensuite avec cette nouvelle vitesse constante jusqu’en C.
En itérant ce procédé, la planète suit le parcours A, B, C, D, E, F… Newton a montré que tous les triangles SAB, SBC, SCD, SEF ont la même aire : ceci correspond à la seconde loi de Kepler, appelée loi des aires.
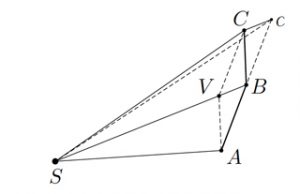
Détail de la figure dessinée par Newton.
Tout d’abord, on remarque que les triangles SAB et SBc ont la même aire, car ils ont la même base AB = Bc et la même hauteur issue du sommet S.
Ensuite, en observant que BcCV est un parallélogramme, on obtient que Cc est parallèle à SB. Les triangles SBc et SBC ont alors la même base SB et les mêmes hauteurs issues de c et C respectivement. Par conséquent, ils ont la même aire.
Ainsi, SAB et SBC sont des triangles de même aire. Ceci permet de démontrer la seconde loi de Kepler : le mouvement d’un corps soumis à une force centrale vérifie la loi des aires.
Le procédé qui permet de passer de A à B, puis de B à C, etc., correspond en fait à une méthode numérique géométrique de calcul, appelée aujourd’hui la méthode d’Euler symplectique, qui sera présentée plus loin. En faisant tendre vers zéro l’intervalle entre chaque impulsion de force, l’approximation ainsi obtenue converge vers la solution du problème.
Comment calculer la position de tous les corps composant le système solaire ?
On considère pour simplifier le système composé de trois corps, le Soleil, Jupiter et Saturne, les trois astres les plus massifs du système solaire. Notons-les \(S\), \(Ju\), et \(Sa\). On fait l’hypothèse que le système est isolé et que les seules forces qui s’exercent sont les forces de gravitation entre les trois corps. Le second principe de Newton, qui dit que la force est égale à la masse fois l’accélération, s’applique ainsi à chaque astre, les masses étant notées m, les accélérations \(\overrightarrow{a}\) et les forces \(\overrightarrow{F}\) :
\[m_{Ju} \overrightarrow{a}_{Ju} = \overrightarrow{F}_{S \rightarrow Ju} + \overrightarrow{F}_{Sa \rightarrow Ju},\\ m_{Sa} \overrightarrow{a}_{Sa} = \overrightarrow{F}_{S \rightarrow Sa} + \overrightarrow{F}_{Ju \rightarrow Sa},\\ m_{S} \overrightarrow{a}_{S} = \overrightarrow{F}_{Ju \rightarrow S} + \overrightarrow{F}_{Sa \rightarrow S}.\]
Derrière ces équations se cachent des équations différentielles, c’est-à-dire des équations dont l’inconnue n’est pas un nombre, mais une fonction, et qui font intervenir une ou plusieurs dérivées de cette fonction. En effet, par définition, lorsqu’on dérive la fonction \(q(t)\) qui donne la position d’un objet au cours du temps, on obtient les coordonnées de la vitesse instantanée \(\overrightarrow{v}(t)\). En dérivant à nouveau, on obtient l’accélération \(\overrightarrow{a}(t)\). Autrement dit :
\(\overrightarrow{v}(t)\) a pour coordonnées \(q′(t)\),
\(\overrightarrow{a}(t)\) a pour coordonnées \(q′′(t)\).
De plus, il est commode d’introduire, au lieu de la vitesse, la quantité de mouvement \(\overrightarrow{p}\) qui est définie par \(\overrightarrow{p}(t) = m \overrightarrow{v}(t)\). En effet, la quantité de mouvement totale du système Soleil-Jupiter-Saturne est conservée au cours du temps :
\[\overrightarrow{p}_{S}(t) + \overrightarrow{p}_{Ju}(t) + \overrightarrow{p}_{Sa}(t) = Constante\]
Finalement, pour chaque planète, il s’agit de résoudre six équations différentielles dont les inconnues sont sa position dans un repère (définie par 3 coordonnées), et sa quantité de mouvement (également définie par 3 coordonnées). Pour un système à trois corps évoluant dans l’espace à 3 dimensions, on doit donc résoudre un système de 18 équations différentielles avec en tout 18 inconnues.
En pratique, il est souvent difficile, voire impossible, de trouver une formule simple pour la solution exacte d’une équation différentielle. On utilise alors des méthodes numériques pour calculer une solution approchée. Les méthodes numériques servant à résoudre des équations différentielles reposent sur un découpage du temps en petits intervalles appelés « pas de temps » et sur une approximation des dérivées.
Comment choisir une méthode numérique ?
Pour des problèmes possédant une structure géométrique particulière, il est essentiel d’utiliser des méthodes numériques, dites géométriques, préservant les invariants du système, afin d’obtenir un bon comportement qualitatif de la solution numérique.
Dans le cas du système solaire, les principaux invariants du modèle sont :
- La quantité de mouvement, parce que le système est isolé : une autre façon de le dire est l’invariance par translation du modèle. On peut choisir un référentiel (système de coordonnées) avec une origine quelconque.
- Le moment cinétique (ou angulaire), parce que les forces sont centrales : une autre façon de le dire est l’invariance par rotation du modèle. En particulier, les trajectoires des planètes sont dans un plan. Dans le cas du problème à 2 corps, cela se traduit par la loi des aires.
- L’énergie, parce qu’il n’y a pas de force de frottement (force conservative) : l’énergie est la somme de l’énergie cinétique (due à la vitesse) et de l’énergie potentielle (due à la gravitation).
Il s’agit ici de trouver une méthode qui, en particulier, préserve bien l’énergie, l’invariant le plus difficile à conserver. Les deux autres invariants, quantité de mouvement et moment cinétique, seront également conservés.
Les méthodes d’Euler
Pour résoudre une équation différentielle de la forme \(y'(t)=f(y(t))\), les méthodes numériques reposent sur la même idée que celle utilisée par Newton pour démontrer la loi des aires : on choisit une impulsion ou pas de temps \(h\), et on calcule une approximation \(y_n ≃ y(t_n)\) de la solution continue à chaque instant \(t_n = nh\), pour \(n = 0, 1, 2, 3…\) La quantité \(y_0\) est connue, c’est la donnée initiale. Ensuite, on calcule \(y_1\), puis \(y_2\), puis \(y_3\), et ainsi de suite.
Les méthodes d’Euler ont pour idée commune d’approcher la dérivée par un taux d’accroissement entre deux instants. La plus simple a été proposée par le mathématicien Leonhard Euler vers 1770. Elle est appelée méthode d’Euler explicite, car le taux d’accroissement est exprimé en fonction de la position occupée à l’instant précédent, qui est connue. Pour une équation de la forme \(y'(t)=f(y(t))\), on utilise donc \(y_{n+1} = y_n + h f(y_n)\).
La deuxième méthode est appelée méthode d’Euler implicite, car le taux d’accroissement est exprimé en fonction de la position qui sera occupée à l’instant suivant, celle précisément que l’on cherche à calculer. Pour une équation de la forme \(y'(t)=f(y(t))\), on utilise donc \(y_{n+1} = y_n + h f(y_{n+1})\).
Enfin, la méthode d’Euler symplectique applique successivement les méthodes explicite et implicite, en deux étapes. À chaque pas de temps, pour la première équation, concernant la dérivée de la position, on utilise la méthode explicite, puis pour la deuxième équation, concernant la dérivée de la vitesse, on utilise la méthode implicite.
Ces méthodes sont présentées en détail sur des exemples plus simples dans la deuxième partie de ce document.
Comparaison des résultats
Nous vous proposons d’observer sur une animation le comportement de différentes méthodes appliquées au système Soleil-Jupiter-Saturne : les trois méthodes d’Euler, ainsi qu’une autre méthode symplectique, celle de Störmer-Verlet.
Ici, le programme représente les trajectoires par rapport au Soleil qui est choisi comme référentiel, donc positionné au centre.
Applet Java réalisée par Gilles Vilmart.
On constate que la méthode d’Euler explicite a un très mauvais comportement qualitatif : les planètes spiralent vers l’extérieur. De même, la méthode d’Euler implicite n’a pas du tout le comportement attendu : elle voit Jupiter s’écraser dans le Soleil. À l’inverse, pour la méthode d’Euler symplectique, comme pour celle de Störmer-Verlet, les planètes conservent des orbites presque elliptiques, on obtient un bon comportement qualitatif.
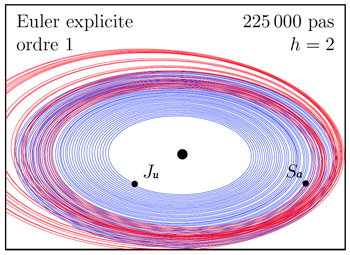
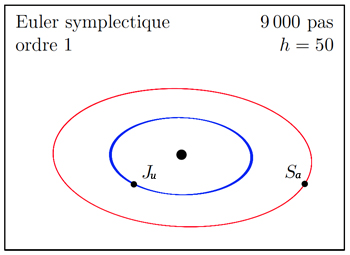
On peut comprendre ces résultats en examinant la conservation de l’énergie. La méthode d’Euler symplectique, comme les autres méthodes symplectiques, préserve bien l’énergie, l’invariant clé de ce système mécanique, alors que les méthodes d’Euler explicite ou implicite, et plus généralement les méthodes explicites standard, ne la conservent pas. Elles ne sont donc pas adaptées à une intégration sur des durées de temps longues.
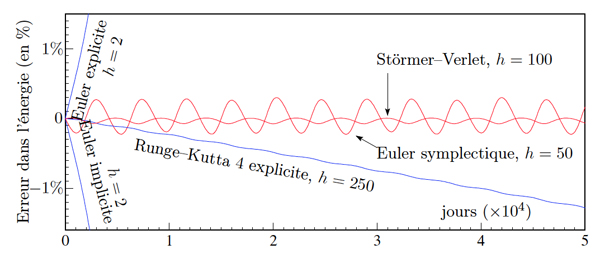
Comparaison de la conservation numérique de l’énergie pour différents intégrateurs numériques pour le système Soleil-Jupiter-Saturne. Les méthodes symplectiques, comme Euler symplectique ou Störmer-Verlet, conservent bien l’énergie sur des temps très longs.
Pour réaliser vous-même l’expérience, vous pouvez programmer ces méthodes à l’aide du logiciel libre Scilab.
On représente les positions des astres par des fonctions du temps \(q_i(t) \in \mathbb{R}^3\), \(i=0, 1, 2\) où l’indice \(i=0\) correspond au Soleil, l’indice \(i=1\) correspond à Jupiter, et l’indice \(i=2\) correspond à Saturne. Les masses respectives de ces astres sont notées \(m_i\), \(i=0,1,2\). On considère aussi les quantité de mouvement \(p_i(t) = m_i q_i′(t)\). On donne dans la table suivante les positions et vitesses initiales (vecteurs de \(\mathbb{R}^3\)) pour le Soleil, Jupiter et Saturne à une date fixée, exprimées en unités astronomique (1 U.A. = 149 597 870 km), le temps étant exprimé en jours terrestres.
| Astre | masse (relativement au Soleil) | position (U.A.) | vitesse (U.A./jour) |
|---|---|---|---|
| Soleil | \(m_0\) = 1.00000597682 (en incluant les planètes du système solaire interne) | 0 | 0 |
| 0 | 0 | ||
| 0 | 0 | ||
| Jupiter | \(m_1\) = 0.000954786104043 | −3.5023653 | 0.00565429 |
| −3.8169847 | −0.0412490 | ||
| −1.5507963 | −0.00190589 | ||
| Saturne | \(m_2\) = 0.000285583733151 | 9.0755314 | 0.00168318 |
| −3.0458353 | 0.00483525 | ||
| −1.6483708 | 0.00192462 | ||
| Constante de gravitation \(G=2.95912208286 \cdot 10^{-4}\) | |||
Données pour le Soleil, Jupiter, Saturne le 05/09/1994 à 0h00, Source : E. Hairer, C. Lubich, and G. Wanner. Geometric Numerical Integration. Structure-Preserving Algorithms for Ordinary Differential Equations. Table I.2.2, page 14, où les paramètres d’autres planètes sont également disponibles.
Voici un exemple de code Scilab d’une trentaine de lignes pour calculer l’évolution du système Soleil-Jupiter-Saturne à l’aide de la méthode d’Euler symplectique. Remarquez que le Soleil lui-même se déplace légèrement (c’est d’ailleurs généralement ainsi qu’on détecte les exoplanètes), mais le programme représente les trajectoires par rapport au Soleil qui est choisi comme référentiel, donc positionné au centre. D’abord les fonctions auxiliaires, à placer dans un fichier euler.sci.
function f=fun_v(q)
deff(’[v]=vecf(v0)’,’v=v0/norm(v0).^3’);
soleil=1:3;jupiter=4:6;saturne=7:9;
f(soleil) =-G*m0*m1*vecf(q(soleil) -q(jupiter))..
-G*m0*m2*vecf(q(soleil) -q(saturne));
f(jupiter) =-G*m1*m0*vecf(q(jupiter)-q(soleil))..
-G*m1*m2*vecf(q(jupiter)-q(saturne));
f(saturne) =-G*m2*m0*vecf(q(saturne)-q(soleil))..
-G*m2*m1*vecf(q(saturne)-q(jupiter));
endfunction
function f=fun_u(p)
f=[p(1:3)/m0;p(4:6)/m1;p(7:9)/m2];
endfunction
function [vp,vq]=euler_symplectique(n,h,p,q)
vp=p;vq=q;
for i=1:n
q=q+h*fun_u(p); p=p+h*fun_v(q);
vq=[vq,q]; vp=[vp,q];
end
endfunction
Ensuite, le fichier principal de calculs, à placer dans un fichier calcul.sce.
//masses des astres, constante de gravitation
m0=1.00000597682;m1=9.54786104043e-4;m2=2.85583733151e-4;
G=2.95912208286e-4;
//conditions initiales
q0=[0;0;0; -3.5023653; -3.8169847; -1.5507963;..
9.0755314; -3.0458353; -1.6483708];
p0=[0;0;0;0.00565429*m1;-0.00412490*m1;-0.00190589*m1;..
0.00168318*m2;0.00483525*m2;0.00192462*m2];
//integration sur un temps 3000*50 jours = 411 annees.
[vp,vq]=euler_symplectique(3000,50,p0,q0)
//representation des trajectoires de Jupiter et Saturne
vq(4:6,:)=vq(4:6,:)-vq(1:3,:); //dans le referentiel du Soleil
vq(7:9,:)=vq(7:9,:)-vq(1:3,:); //(Soleil place au centre)
plot([vq(4,:)’,vq(7,:)’],[vq(5,:)’,vq(8,:)’]);
//utiliser comet3d pour obtenir une animation 3D.
comet3d([vq(4,:)’,vq(7,:)’],[vq(5,:)’,vq(8,:)’],[vq(6,:)’,vq(9,:)’]);
2. Des méthodes numériques
De nombreux phénomènes physiques, comme celui présenté en première partie de ce document, peuvent être modélisés par des équations différentielles, c’est-à-dire des équations dont l’inconnue n’est pas un nombre, mais une fonction, et qui font intervenir une ou plusieurs dérivées de cette fonction. En pratique, il est souvent difficile, voire impossible, de trouver une formule simple pour la solution exacte d’une équation différentielle. On utilise alors des méthodes numériques pour calculer une solution approchée.
Un exemple d’équation différentielle : le problème de De Beaune (1638)
Afin d’illustrer de façon détaillée les méthodes de résolution numériques, considérons d’abord un problème d’équation différentielle simple, formulé par le mathématicien amateur Florimond de Beaune en 1638. Il s’agit de trouver une courbe \(\mathcal{C}\) du plan, donnée par une fonction \(y(t)\), telle que la tangente à \(\mathcal{C}\) en tout point M d’abscisse t coupe l’axe des abscisses à une distance constante \(D = 1\) de l’abscisse t.
Pour établir l’équation différentielle de ce problème, on remarque que la pente de la tangente au point M est égale au quotient de la hauteur \(y(t)\) sur la largeur \(D = 1\) autrement dit, la pente est égale à \(y(t)\). On rappelle de plus que la dérivée d’une fonction en un point est par définition la pente de la tangente au graphe de cette fonction en ce point. Ceci conduit à l’équation différentielle \(y′(t) = y(t)\). Cette équation a pour solution générale \(y(t) = C exp(t)\) (fonction exponentielle), où \(C\) est une constante que l’on peut déterminer en fixant une condition initiale \(y(0) =y_0\). Le problème d’équation différentielle avec valeur initiale possède alors une unique solution \(y(t) = y_0 exp(t)\).
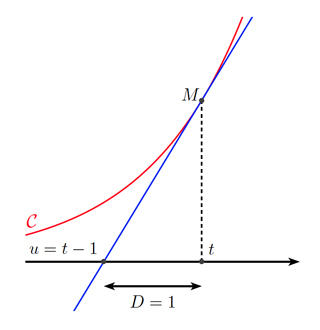
Interprétation géométrique du problème de De Beaune.
Les méthodes ou schémas d’Euler calculent aux pas de temps \(t_1 =h\), \(t_2=2h\), …, \(t_n =nh\)… les approximations \(y_1\), \(y_2\), …, \(y_n\)… de la solution exacte \(y(nh)\).
La méthode d’Euler explicite remplace la dérivée \(y'(t)\) par le taux d’accroissement \(\frac{y_{n + 1} – y_n} {h}\) et l’équation \(y'(t)=y(t)\) est approchée par \(\frac{y_{n + 1} – y_n} {h}=y_n\), soit après un petit calcul \(y_{n + 1}=(1 + h) y_n\). On part donc de \(y_0\), on calcule \(y_1=(1 + h)y_0\), puis \(y_2=(1 + h)y_1\), etc. On obtient ainsi une ligne brisée passant par les points \((t_n, y_n)\). On peut montrer qu’en réduisant la taille du pas \(h\), la ligne brisée ainsi obtenue se rapproche de la solution exacte, et converge vers cette solution lorsque le pas \(h\) tend vers zéro. On observe de plus, sur la figure ci-dessous, que chaque fois qu’on divise le pas \(h\) par \(2\), la solution numérique (la ligne brisée en bleu) se rapproche de la solution exacte (la courbe rouge) en divisant l’erreur par \(2\). La vitesse de convergence est proportionnelle à \(h\), donc d’ordre \(1\).
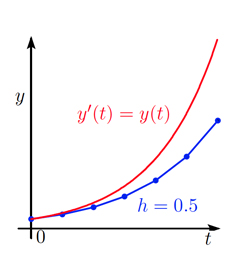
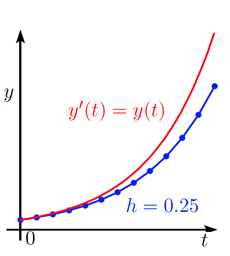
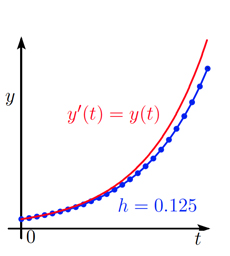
Méthode d’Euler explicite pour résoudre le problème de De Beaune \(y'(t) = y(t)\), avec \(y\)(0) = 1. Pas de temps \(h\) = 0.5, 0.25 et 0.125, respectivement.
Il existe de nombreuses méthodes numériques plus précises, où cette distance est proportionnelle à \(h^2\), \(h^3\), etc., ce qui correspond à une vitesse de convergence d’ordre \(2\), \(3\), etc.
Le schéma d’Euler implicite est aussi un schéma d’ordre \(1\), dans lequel l’équation \(y’(t)=y(t)\) est approchée par \(\frac{y_{n + 1}-y_n}{h}=y_{n + 1}\), soit après un petit calcul \(y_{n + 1}=\frac{y_n}{1-h}\). Ce schéma est choisi pour résoudre certaines équations différentielles, afin de garantir une stabilité des calculs. En effet, avec le schéma d’Euler explicite, il faut souvent choisir un pas de temps très petit pour éviter que les valeurs approchées n’explosent vers des nombres de plus en plus grands.
Pour certains problèmes, la vitesse de convergence et la stabilité ne sont pas les seuls aspects à prendre en compte, car il est aussi important d’avoir un comportement qui respecte la physique du problème, notamment en conservant des invariants, par exemple l’énergie dans le cas du système Soleil-Jupiter-Saturne.
Comment conserver l’énergie du système ?
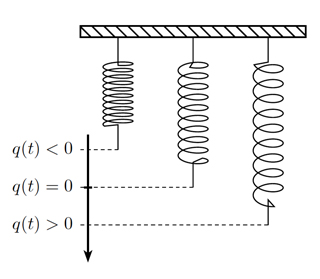
Un ressort qui oscille.
Considérons à présent l’exemple d’un ressort qui oscille autour de sa position de repos. En l’absence de toute force de frottement (pas d’amortissement) et en négligeant la force de gravitation, on peut modéliser ce mouvement par un système de deux équations différentielles. L’extrémité du ressort se déplace selon un axe vertical, sa position \(q(t)\) est donc déterminée par une coordonnée. L’origine est la position au repos, \(q(t) > 0\) si le ressort est étiré, et \(q(t) < 0\) si le ressort est comprimé.
Il s’agit maintenant de modéliser le mouvement du ressort. Le ressort possède une certaine quantité de mouvement \(p(t) = m v(t)\). Comme dans le cas des planètes, on peut écrire cette équation sous la forme \(p(t) = m q’(t)\), où la dérivée \(q’(t)\) est la vitesse.
Une deuxième équation s’obtient à l’aide des deux faits suivants : le premier dit qu’un ressort étiré (ou comprimé) de \(q(t)\) unités par rapport à sa longueur naturelle au repos exerce une force de rappel \(- k q(t)\) proportionnelle à \(q(t)\) et de direction opposée, où \(k\) est une constante positive qui donne la raideur du ressort. Le second fait est la deuxième loi de Newton, qui dit que la force est égale à la masse fois l’accélération : \(\overrightarrow{F}(t) = m \overrightarrow{a}(t)\).
Or \(\overrightarrow{a}(t)\) a pour coordonnées \(q′′(t)\). On en déduit \(-k q(t) = m q′′(t) = p'(t)\), ce qui donne la seconde équation différentielle.
Comme la force \(\overrightarrow{F}\) est conservative, l’énergie totale du système \(E(t)\) est conservée. Ici, on peut la calculer facilement : c’est la somme de l’énergie cinétique liée à la vitesse et de l’énergie potentielle liée au ressort. On a \(E(t) = E(p(t), q(t)) = \frac{1}{2m} p(t)^2 + \frac{1}{2} k q(t)^2\).
\(E(t) = E(p(t), q(t)) = \frac{1}{2m} p(t)^2 + \frac{1}{2} k q(t)^2\)
On a : \(p(t) = m q′(t)\) et \(- k q(t) = p′(t)\)
On dérive \(E(t)\) :
\(E′(t) = \frac{1}{2m} 2 p(t)p′(t) + \frac{1}{2} k 2 q(t) q′(t)\)
On remplace \(p(t)\) et \(p′(t)\) en fonction de \(q(t)\) et \(q′(t)\) :
\(E′(t) = \frac{1}{m} m q′(t) (- k q(t)) + k q(t) q′(t)\)
\(E′(t) = – k q(t) q′(t) + k q(t) q′(t)\)
\(E′(t) = 0\)
En dérivant \(E(t)\), on obtient après calcul \(E’(t)= 0\). Cela montre que l’énergie reste constante au cours du temps, elle est donc bien un invariant du système.
Appliquons maintenant le schéma numérique d’Euler explicite. À chaque pas de temps, on remplace les dérivées par des quotients et les valeurs de \(p(t), q(t)\) par leurs approximations à l’instant \(t_n\) :
\[\frac{q_{n + 1}-q_n}{h}=\frac{1}{m} p_n, \frac{p_{n + 1}- p_n}{h}=-k q_n\]
\(E(p_{n+1}, q_{n+1}) = \frac{1}{2m} p_{n+1}^2 + \frac{1}{2} k q_{n+1}^2\)
On a : \(q_{n+1} = q_n + \frac{h}{m} p_n\) et \(p_{n+1} = p_n – k h q_n\)
On remplace :
\(E(p_{n+1}, q_{n+1}) = \frac{1}{2m} (p_n – k h q_n)^2 + \frac{1}{2} k (q_n + \frac{h}{m} p_n)^2\)
\(E(p_{n+1}, q_{n+1}) = \frac{1}{2m} (p_n^2 – 2 k h p_n q_n + k^2 h^2 q_n^2) + \frac{1}{2} k (q_n^2 + 2 \frac{h}{m} q_n p_n + \frac{h^2}{m^2} p_n^2)\)
\(E(p_{n+1}, q_{n+1}) = \frac{1}{2m} p_n^2 + \frac{1}{2} k q_n^2 + k \frac{h^2} {m} (\frac{1}{2m} p_n^2 + \frac{1}{2} k q_n^2) + (- 2 k \frac{h}{2m} p_n q_n + 2 k \frac{h}{2m} p_n q_n)\)
Or \(E(p_n, q_n) = \frac{1}{2m} p_n^2 + \frac{1}{2} k q_n^2\)
Donc \(E(p_{n+1}, q_{n+1}) = (1 + \frac{k h^2} {m}) E(p_n, q_n)\)
L’énergie est aussi approchée et le calcul montre que \(E(p_{n + 1}, q_{n + 1})= (1 + \frac{k h^2}{m}) E(p_n, q_n)\). À chaque pas de temps, l’énergie approchée n’est plus constante mais est amplifiée par le facteur \(1 + \frac{k h^2}{m}\), qui est strictement plus grand que \(1\).
Avec la méthode d’Euler implicite, les valeurs de \(p(t), q(t)\) sont remplacées par leurs approximations à l’instant \(t_{n + 1}\) :
\[\frac{q_{n + 1}-q_n}{h}=\frac{1}{m} p_{n + 1}, \frac{p_{n + 1}- p_n}{h}=-k q_{n + 1}\]
\(E(p_{n+1}, q_{n+1}) = \frac{1}{2m} p_{n+1}^2 + \frac{1}{2} k q_{n+1}^2\)
On a maintenant : \(q_{n+1} = q_n + \frac{h}{m} p_{n+1}$ et $p_{n+1} = p_n – k h q_{n+1}\)
ce qui peut s’écrire : \(q_n = q_{n+1} – \frac{h}{m} p_{n+1}\) et \(p_n = p_{n+1} + k h q_{n+1}\)
Ces expressions sont les mêmes que celles utilisées pour le schéma d’Euler explicite, à quelques différences près : ce sont \(q_n\) et \(p_n\) qui sont exprimés en fonction de \(q_{n+1}\) et \(p_{n+1}\), et \(h\) est changé en \((-h)\). On dit que les méthodes d’Euler explicite et implicite sont adjointes.
À partir de cette constatation, il suffit de répercuter ces modifications dans l’expression de l’énergie approchée pour obtenir le résultat correspondant au schéma d’Euler implicite.
On obtient alors :
\(E(p_n, q_n) = (1 + \frac{k h^2} {m}) E(p_{n+1}, q_{n+1})\)
soit \(E(p_{n+1}, q_{n+1}) = \frac{1}{1+\frac{k h^2}{m}} E(p_n, q_n)\)
Le calcul montre cette fois que \(E(p_{n + 1}, q_{n + 1})=\frac{1}{1 + \frac{k h^2}{m}} E(p_n, q_n)\). À chaque pas de temps, l’énergie n’est pas constante mais est atténuée par le facteur \(\frac{1}{1 + \frac{k h^2}{m}}\) strictement inférieur à \(1\).
La méthode d’Euler symplectique : une méthode qui préserve bien l’énergie
Pour conserver correctement l’énergie, l’idée est de mélanger les méthodes d’Euler implicite et explicite. Pour le problème du ressort, la méthode d’Euler symplectique s’écrit :
\[\frac{q_{n + 1}-q_n}{h} = \frac{1}{m} p_n, \frac{p_{n + 1}- p_n}{h}=-k q_{n 1}\]
On remarque que cette méthode fait bouger la position et la quantité de mouvement alternativement, comme dans la preuve de Newton de la loi des aires décrite précédemment. Ainsi, la preuve de Newton utilise un schéma symplectique.
Ce schéma ne conserve pas l’énergie, mais conserve une énergie numérique modifiée. Cette énergie modifiée est définie par \(E_h (p, q) = E(p, q) + h \frac {k}{m} p q\).
Un calcul montre que \(E_h (p_{n + 1}, q_{n + 1}) = E_h (p_n, q_n)\), c’est-à-dire que l’énergie numérique modifiée est exactement conservée par la méthode symplectique, sans aucun facteur d’amplification ou d’atténuation. Cette énergie numérique est une petite perturbation de taille \(h\) de l’énergie exacte \(E\), et l’erreur dans l’énergie de la solution numérique reste petite, de taille \(h\).
La méthode d’Euler symplectique est donc un schéma (ou intégrateur) géométrique adapté au problème, car elle conserve presque l’énergie du système.
Cette méthode, comme les autres méthodes d’Euler, est d’ordre \(1\). Une autre méthode symplectique, celle de Störmer-Verlet, qui conserve aussi une énergie numérique modifiée, est d’ordre \(2\).
Visualisation de l’énergie
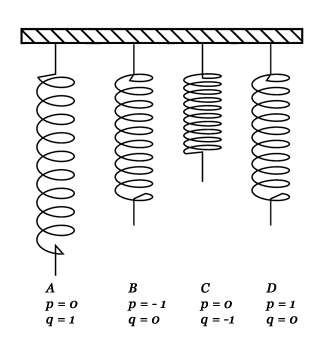
Le ressort oscille entre 4 positions, avec m = 1 et k = 1.
Un état du ressort en un instant donné correspond à la connaissance de sa position et de sa quantité de mouvement. Choisissons pour simplifier \(m = 1\) et \(k = 1\). Supposons de plus qu’à \(t = 0\), le ressort est étiré et immobile, autrement dit \(q_0 = 1, p_0 = 0\). Le ressort oscille entre quatre positions : A avec étirement maximum et vitesse nulle \(q = 1\) et \(p = 0\), B avec étirement nul et vitesse minimale \(q = 0\) et \(p = -1\), C avec étirement minimum et vitesse nulle \(q = -1\) et \(p = 0\), D avec étirement nul et vitesse maximale \(q = 0\) et \(p = 1\).
On représente souvent le mouvement dans l’espace des phases, un système de coordonnées 2D, avec \(q(t)\) en abscisse et \(p(t)\) en ordonnée. Avec les données choisies, l’énergie vaut \(E(t) = \frac{1}{2} (p(t)^2 + q(t)^2) = \frac{1}{2}\), autrement dit le point de coordonnées \((p(t), q(t))\) est toujours sur le cercle de centre 0 et de rayon 1, d’équation \(p^2 + q^2 = 1\). Ce cercle correspondant à la solution exacte est représenté en rouge sur les figures ci-dessous.
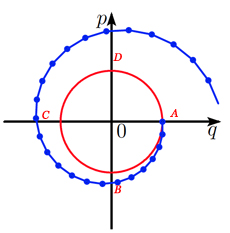
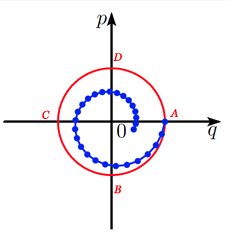
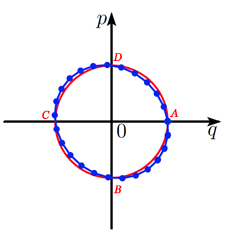
Comparaison des méthodes d’Euler explicite, implicite et symplectique pour le problème du ressort avec k = 1.
La solution approchée calculée avec la méthode d’Euler explicite amplifie l’énergie. Les points calculés \((p_n , q_n)\) s’éloignent du cercle, en formant une spirale vers l’extérieur. Avec Euler implicite, les points \((p_n , q_n)\) se rapprochent du centre du cercle, en formant une spirale vers l’intérieur, illustrant l’atténuation de l’énergie.
La méthode symplectique, par contre, conserve presque l’énergie. Les points \((p_n , q_n)\) restent sur une ellipse, d’autant plus proche du cercle que \(h\) est petit.
Une théorie mathématique, appelée analyse rétrograde, permet de démontrer que les intégrateurs symplectiques présentent une bonne conservation de l’énergie d’un tel système. On peut démontrer que ces intégrateurs préservent une énergie numérique modifiée, ainsi que nous l’avons expliqué pour la méthode d’Euler symplectique appliquée au problème du ressort. Ces méthodes symplectiques sont donc bien adaptées à une intégration sur des intervalles de temps longs et en particulier pour déterminer la position des planètes.
- E. Hairer, C. Lubich, G. Wanner Geometric Numerical Integration. Structure-Preserving Algorithms for Ordinary Differential Equations. Springer Series in Computational Mathematics 31. Springer-Verlag, Berlin, 2nd ed. 2006.
- J. Laskar, A. Fienga, M. Gastineau, H. Manche. La2010: A new orbital solution for the long term motion of the Earth. preprint, arXiv: 1103.1084, 2011
- B. Leimkuhler, S. Reich. Simulating Hamiltonian Dynamics. Cambridge Monographs on Applied and Computational Mathematics 14. Cambridge University Press, Cambridge, 2004.
- A. Ostermann, G. Wanner. Geometry by its History. Undergraduate Texts in Mathematics. Springer-Verlag, New-York, 2012.
Cet article est publié sous la licence CreativeCommons Attribution – Partage dans les Mêmes Conditions 4.0 (CC-BY-SA 4.0).
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Gilles Vilmart
Enseignant-chercheur à l'Université de Genève, Section de Mathématiques.

Shaula Fiorelli Vilmart