
Mona Lisa au photomaton
Regardez attentivement la série de 9 images A, B, C, D, E, F, G, H, I. Chacune a été obtenue à partir de la précédente en réduisant la taille de l’image de moitié, ce qui a donné quatre morceaux analogues qu’on a placés en carré pour obtenir une image ayant la même taille que l’image d’origine. Le nombre de pixels a été exactement conservé et en fait, on a seulement déplacé les pixels pour avoir quatre réductions de l’image initiale. Cette transformation s’appelle la transformation du photomaton.

L’image B comporte 4 Mona Lisa. L’image C en comporte 16. L’image D en comporte 64, etc. Il se produit quelque chose d’étrange car, au bout de neuf étapes, l’image de Mona Lisa est réapparue. Précisons que c’est bien la même transformation qui a été utilisée pour déduire les unes après les autres les images de la série (c’est un programme d’ordinateur réalisé par Philippe Mathieu qui a fait le travail à chaque fois).
Savez-vous expliquer le paradoxe graphique de la réapparition de l’image initiale ?
La solution est mathématique et s’appliquerait à toute transformation déplaçant les pixels d’une image. Puisque seuls des déplacements de pixels sont opérés d’une image à l’autre, cela signifie que la transformation est ce qu’en mathématiques on appelle une permutation des pixels.

Notons p cette permutation. Sur le dessin ci-dessus, on a :
B = p(A), C = p(p(A)), etc.
On sait que les permutations d’un ensemble fini constituent un groupe, ce qui signifie (entre autres choses) qu’il existe un entier k, tel que p opéré k fois est la transformation identité (c’est-à-dire l’opération qui ne change rien). Cela explique pourquoi on revient à l’image initiale.
Ce résultat peut sembler un peu abstrait, en réalité il est facile : lorsque l’on opère des modifications d’ordre bien précises et qu’on les recommence, on finit toujours par revenir à son point de départ. Voici un exemple simple qui fera comprendre l’idée.
Dans une liste de 5 objets, on échange le premier et le troisième, et, en même temps, on fait passer le deuxième en position 4, celui qui est en position 4 est mis en position 5 et celui qui est en position 5 est mis en position 2 : abcde → ceabd.
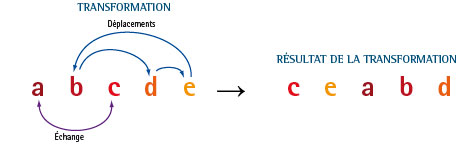
Si, partant de abcde, on recommence sans cesse cette transformation, on obtient successivement les agencements décrits dans l’illustration ci-dessous. On est revenu au point de départ en 6 étapes.
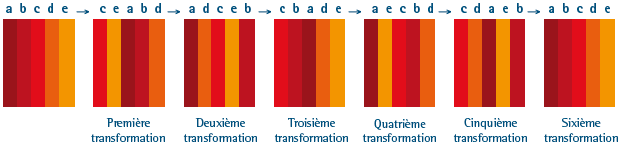
Avec nos pixels, la situation était analogue, et donc on était certain dès le départ que l’image initiale réapparaîtrait. Pour justifier qu’elle réapparaît à la huitième itération exactement (ni avant, ni après), il faut entrer dans le détail de la définition de la transformation du photomaton.
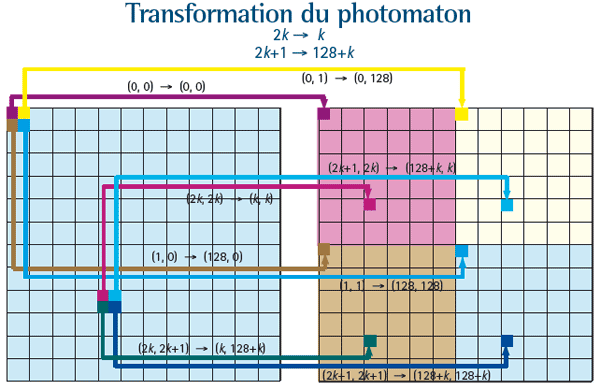
L’image utilisée comporte 256 lignes et 256 colonnes numérotées de 0 à 255. La transformation du photomaton consiste à réaliser l’opération suivante sur les numéros des lignes : on prend les lignes de rang pair qu’on fait suivre de celles de numéro impair. De même, pour les numéros des colonnes — cela explique l’apparition de quatre versions en plus petit de l’image initiale. Le pixel (0, 0) reste donc en position (0, 0) ; le pixel (1, 0) passe en position (128, 0) ; le pixel en position (1, 1) passe en position (128, 128) ; le pixel en position (4, 5) passe en position (2, 130), etc. (pour un numéro pair 2k on passe à k, pour un numéro impair 2k + 1 on passe à 128 + k). L’étude de cette transformation n’est pas très difficile (elle peut aussi être simulée par ordinateur) et conduit au résultat qu’en huit étapes exactement, chaque pixel est revenu à sa place.
Pour expérimenter vous-même de telles transformations, nous vous proposons une applet réalisée par M. Braure, M. Dref, N. Kondratek, sous la direction de Philippe Mathieu.
Cette applet vous permet de charger une image de votre choix et de choisir une transformation (19 sont programmées) (onglet Paramètres), de lui appliquer différentes transformations Image Transformée, de calculer le temps de retour, d’aller en accès direct à l’itération n sans passer par les précédentes, de sauvegarder toutes les images obtenues, de visualiser les cheminements de points d’une transformation sur une image donnée (onglet Visualisation), d’appliquer des chaines de transformations et enfin d’intégrer un texte dans l’image afin de pratiquer la stéganographie (onglet Cryptage).
Si l’applet ne s’affiche pas correctement, vous pouvez télécharger et ouvrir l’application Java autonome correspondante.
Un groupe est un ensemble d’éléments qui muni d’une opération satisfaisant les propriétés suivantes. Le résultat de l’opération doit être un élément de l’ensemble (propriété de fermeture). De plus, l’opération doit être commutative, associative, elle doit avoir un élément neutre et chaque élément de l’ensemble doit avoir un inverse pour l’opération. Ces propriétés sont exactement celles que possède l’opération d’addition des nombres entiers.
Considérons l’ensemble {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11}.
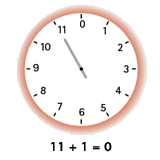
Définissons une opération d’addition des éléments de cet ensemble basée sur le principe de l’« horloge » illustrée à droite.
On a alors : 11 + 1 = 0, 9 + 3 = 0, etc.

On remarque qu’à partir de n’importe quelle heure, si on additionne, par exemple, quatre de façon répétitive, on revient inévitablement à la même « heure ». C’est le même principe que la transformation du photomaton.
On peut montrer que l’ensemble {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11} muni de l’addition sur le principe de cette horloge, a une structure de groupe.
Pour plus de détails, voir la page web de Philippe Mathieu sur les transformations bijectives d’images, ainsi que deux articles de la revue Pour la Science : Images brouillées, images retrouvées et Une scytale informatique.
Une première version de ce document est parue dans la revue Accromath réalisée par l’Institut des sciences mathématiques et le Centre de recherches mathématiques du Québec, Volume 6, Été-automne 2011 et Volume 7, Hiver-Printemps 2012.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Jean-Paul Delahaye
Professeur émérite d'informatique à l'Université des Sciences et Technologies de Lille (Lille 1) et chercheur au Centre de recherche en informatique, signal et automatique de Lille (CRIStAL).