
Planifiez vos tête-à-tête avec les graphes à des fins de distanciation
Imaginons que la direction de votre entreprise ait établi une liste de tête-à-tête qui doivent se tenir pour mettre en place un nouveau projet. Pour simplifier, disons que chaque tête-à-tête a une durée d’1 heure et que leur ordre n’a pas d’importance mais que la décision finale ne peut être prise que s’ils ont tous eu lieu. Examinons un exemple et pour cela, supposons que les tête-à-tête à faire sont représentés par le dessin ci-dessous, qui est ce que l’on appelle un graphe (voir aussi l’article « La vie secrète des graphes » sur theconversation.com).
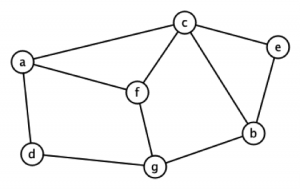 Chaque rond est appelé un sommet. Chaque sommet représente ici une personne impliquée dans le projet. Si 1 tête-à-tête est planifié par la direction, une liaison, appelée arête, est placée entre les 2 sommets qui correspondent aux 2 personnes impliquées. Dans l’exemple particulier ci-dessus, 10 tête-à-tête doivent être organisés pour un total de 7 personnes. Une organisation très simple consiste à faire ces 10 rencontres les unes après les autres, dans un ordre quelconque. Sachant que chacune d’elles dure 1 heure, la totalité prendra ainsi 10 heures. Comment faire mieux ? L’objet de cet article est de décrire quelques concepts de théorie des graphes utiles dans ce type de situation.
Chaque rond est appelé un sommet. Chaque sommet représente ici une personne impliquée dans le projet. Si 1 tête-à-tête est planifié par la direction, une liaison, appelée arête, est placée entre les 2 sommets qui correspondent aux 2 personnes impliquées. Dans l’exemple particulier ci-dessus, 10 tête-à-tête doivent être organisés pour un total de 7 personnes. Une organisation très simple consiste à faire ces 10 rencontres les unes après les autres, dans un ordre quelconque. Sachant que chacune d’elles dure 1 heure, la totalité prendra ainsi 10 heures. Comment faire mieux ? L’objet de cet article est de décrire quelques concepts de théorie des graphes utiles dans ce type de situation.
Examinons un peu plus en détails notre exemple. Tous les participants ne sont pas logés à la même enseigne. Par exemple, d n’a que 2 tête-à-tête à faire, alors que f en a 3. Le nombre d’arêtes dans lesquelles se trouve un sommet est appelé son degré. Le degré de a est 3, celui de d est 2, etc. Le degré du sommet c est 4, ce qui est le maximum. Ainsi, la totalité des rencontres durera au minimum 4 heures en tout (car c doit faire 4 réunions de 1 heure chacune et qu’il ne peut pas en faire 2 en même temps). Le sommet c joue donc un rôle particulier ici puisque c’est lui qui induit le plus de contraintes. Par la suite, nous noterons par la lettre grecque Δ le degré maximal d’un graphe (soit le maximum des degrés d’un graphe). Si le graphe qui représente tous les tête-à-tête à faire a un degré maximum Δ, alors la durée totale sera d’au moins Δ heures. Mais est-il toujours possible de réaliser tous les tête-à-tête en Δ heures ? Essayons sur notre exemple pour lequel Δ = 4. Voici une planification représentée ci-après. Chaque couleur indique un créneau horaire. Par exemple Rouge = 8h − 9h, Bleu = 9h − 10h, Vert = 10h− 11h et Gris = 11h − 12h.
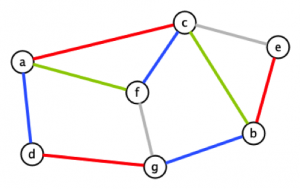 Cette planification permet de faire toutes les rencontres en Δ = 4 heures. Nous avons donc une solution égale au degré maximal du graphe.
Cette planification permet de faire toutes les rencontres en Δ = 4 heures. Nous avons donc une solution égale au degré maximal du graphe.
Pour planifier, nous avons simplement colorié les arêtes du graphe avec la contrainte que si 2 arêtes ont une même extrémité (une même personne dans 1 tête-à-tête), alors elles doivent avoir une couleur différente (un créneau horaire différent). Les remarques entre parenthèses sont la traduction des propriétés du graphe selon les contraintes d’organisation. Nous remarquerons ici que la coloration est faite sur les arêtes et non sur les sommets (la coloration des sommets est un sujet classique en théorie des graphes, voir l’article « Comment élaborer un planning ? Avec des crayons de couleur, de la patience et… des mathématiques »).
Ainsi, le sommet c oblige à utiliser 4 couleurs et on peut voir sur le dessin que 4 couleurs sont suffisantes. Mais ce n’est qu’un exemple particulier. Est-ce possible pour tout graphe ? La réponse est non. Examinons un cycle à 5 sommets, dessiné ci-dessous.
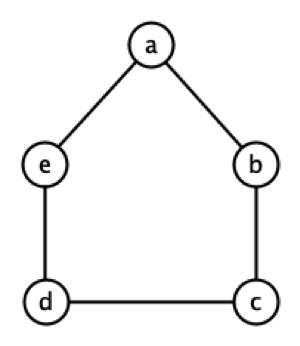
Ici Δ = 2 mais il n’est pas possible de colorier les arêtes avec seulement 2 couleurs. En effet, essayons de colorier avec Rouge et Bleu seulement. Si l’arête ab est coloriée en Bleu, l’arête ae doit être coloriée en Rouge. Ainsi, l’arête ed doit être coloriée en Bleu et bc en Rouge. Reste l’arête dc qui ne peut ainsi pas être coloriée ni en Rouge (à cause de l’arête bc) ni en Bleu (à cause de ed). Il nous faut une troisième couleur, ou un troisième créneau à défaut d’apprendre le don d’ubiquité à nos participants.
S’il est possible de colorier les arêtes d’un graphe de degré maximal Δ avec seulement Δ couleurs, alors nous sommes sûrs d’avoir une solution optimale, impossible de faire mieux. Mais, l’exemple précédent montre que, dans certains cas, plus de Δ couleurs sont nécessaires (ici Δ + 1). Jusqu’où peut-on aller ? Est-ce qu’il existe des graphes de degré maximal Δ qui auraient besoin de Δ + 7 couleurs, voire Δ2 couleurs, voire plus ?
Il a été montré par le mathématicien soviétique et ukrainien Vadim Georgievich Vizing (dans les années soixante) que les arêtes de tout graphe de degré maximal Δ peuvent être coloriées avec au plus Δ + 1 couleurs. Nous sommes donc rassurés, il ne nous faudra qu’un créneau horaire de plus pour simuler notre grande réunion. De plus, des algorithmes efficaces ont été mis au point dans les années quatre-vingts pour colorier tout graphe de degré maximal Δ avec au plus Δ + 1 couleurs. Pour plus de références sur ces travaux et d’autres apparentés, vous pouvez consulter la page Wikipédia sur la coloration d’arêtes (en anglais).
Ainsi exposée, la situation semble claire : il faut au moins Δ couleurs et des algorithmes garantissent de colorier avec au plus Δ + 1 couleurs. Une petite unité sépare donc ce que l’on sait garantir (Δ + 1) et le minimum théorique (Δ). Oui mais cette unité se trouve être au cœur de la complexité algorithmique. En effet, savoir si un graphe de degré maximal Δ a une coloration optimale de ses arêtes de Δ ou de Δ + 1 couleurs est un problème algorithmique difficile. Il fait partie de la vaste classe des problèmes NP-complets. D’autres problèmes de graphes qui ont le même statut sont présentés dans l’article « Des problèmes de graphes faciles à comprendre mais difficiles à résoudre »).
Il est a priori étrange de basculer dans un problème difficile entre Δ et Δ + 1. Le théorème de Vizing nous dit que toute coloration optimale utilise Δ ou Δ + 1 couleurs, pas plus, pas moins. Si l’algorithme évoqué plus haut construit une coloration utilisant Δ couleurs, alors on sait qu’elle est optimale. Mais si la coloration construite utilise Δ + 1 couleurs, cela peut être optimal (rappelez-vous du cas du cycle à 5 sommets vu plus haut) ou pas…
Quelles sont les conséquences concrètes pour nos tête-à-tête ? En fin de compte elles ne sont pas si importantes. Au pire, la session va durer Δ + 1 heures alors qu’elle aurait pu durer Δ heures. Dans notre exemple, il était simple de trouver une solution car nous n’avions pas beaucoup de participants. Le problème aurait été plus complexe si nous avions eu des centaines de participants. Un algorithme est nécessaire. Et la différence d’1 heure qui nous semble si mineure en pratique représente pourtant un gouffre pour l’informatique théorique.
Envie d’en savoir plus sur les graphes ? Consultez la chaîne Youtube de l’auteur.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Christian Laforest
Professeur à l'Université Clermont Auvergne, enseignant à l'institut d'informatique ISIMA et chercheur au laboratoire LIMOS.
