
Quand plus égale moins
Imaginez cela : vous êtes en voiture sur une route de campagne et vous apercevez sur votre droite l’autoroute qui, elle, est vide. Ah si seulement vous pouviez traverser ce champ, vous y seriez en un rien de temps ! Mais non, il va falloir le contourner. Plus tard, vous arrivez en ville. Vous n’êtes plus qu’à quelques pâtés de maisons de votre destination, mais vous êtes coincé dans ces maudits bouchons. Et bien sûr, il n’y a qu’une seule voie de circulation : si seulement les travaux publics avaient eu la bonne idée de réduire un peu la largeur du trottoir pour rajouter une voie de circulation, vous seriez déjà depuis longtemps arrivé à bon port ! Enfin, ça, c’est ce que vous vous dites, car la réalité est peut-être un peu plus complexe que cela : et si ajouter des routes ou augmenter la qualité ou la capacité des routes existantes n’améliorait pas le trafic, voire, étonnamment, allongeait les bouchons ?
C’est la question que s’est posée le mathématicien allemand Dietrich Braess. Pour l’anecdote, il a apporté sa réponse dans un article scientifique en allemand de 1968 qu’il n’a jamais traduit en anglais. Néanmoins, l’impact de sa courte étude a été tel qu’elle a été citée et référencée des milliers de fois, y compris par des chercheurs ne parlant pas allemand, avant d’être finalement traduite en 2005.
Pour comprendre l’effet du retrait d’une route sur le trafic, plusieurs méthodes sont envisageables : on peut faire une expérimentation en fermant une route existante et en mesurant l’impact sur la circulation, ou bien on peut collecter des grands jeux de données de trafic à travers le monde et les analyser pour identifier des similitudes entre les situations. Ces deux approches sont aujourd’hui régulièrement effectuées, mais à son époque Braess ne disposait pas de cette possibilité, et d’ailleurs, il « allait de soi » qu’enlever une route dégraderait la situation. Il avait donc opté pour un modèle mathématique, plus simple à manipuler, et surtout qui permet de comprendre, d’analyser et de caractériser les « familles » de situations dans lesquelles des paradoxes peuvent apparaître. Ainsi, plus de cinquante ans plus tard, ses travaux sont toujours aussi inspirants pour les scientifiques.
En général, le but d’un modèle est de proposer un ensemble d’équations dont la résolution numérique est proche des valeurs que l’on obtiendrait en situation réelle. Ces équations peuvent ensuite être étudiées analytiquement (existence, unicité et propriétés des solutions) ou numériquement sur des ordinateurs, ce qui permet de confronter le modèle à la réalité et ainsi de le confirmer ou de l’infirmer, voire dans certains cas d’expliquer des situations inattendues ou d’anticiper les résultats d’expérimentations réelles.
Revenons à notre question initiale : « existe-t-il des situations dans lesquelles l’ajout de ressources mène à une dégradation des performances pour tous les usagers ?». Dans un raisonnement mathématique, il est généralement plus difficile de montrer la non-existence d’une situation que son existence. En effet, si l’on cherche à montrer qu’ « il est possible » qu’un ajout de ressources dans le système réduise ses performances (ici, le temps de trajet des automobilistes), alors il suffit de trouver un exemple dans lequel ce phénomène apparaît. {Attention : spoiler alert} C’est précisément cela qu’a montré D. Braess dans son article et que nous allons illustrer ici. {Fin du spoiler}
Dans une démarche scientifique, ce raisonnement mathématique peut précéder d’autres travaux. Ainsi, dans un second temps, l’étude peut chercher à identifier les caractéristiques des équations qui mènent à ce type de situations paradoxales. Enfin, dans un troisième temps, arrive la confrontation avec la réalité : existe-t-il effectivement des situations dans lesquelles un tel phénomène se produit ?
Un petit scénario imaginaire (ou « toy example »)
L’exemple suivant a été construit spécifiquement pour montrer ces paradoxes : peut-on concevoir un réseau dans lequel l’ajout de ressources est nuisible aux utilisateurs ? Non seulement nous allons l’observer et le démontrer, mais en plus une petite animation vous permettra de vous en rendre compte par vous-même (voir plus bas). Cet exemple est dérivé de celui fourni par D. Braess, et comme celui-ci, est minimal en termes de nombres de liens utilisés.
Voici comment l’exemple a été construit.
Considérons le petit réseau représenté sur la figure ci-dessous. On suppose que tous les usagers cherchent à se rendre du point A au point D. Pour cela, ils ont initialement deux chemins possibles, chacun étant constitué de deux rues ou deux tronçons.
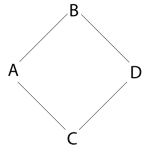
Figure 1
Le modèle mathématique
Le temps que met un utilisateur pour traverser un tronçon dépend des spécificités intrinsèques de ce dernier (nombres de voies par exemple) et de la densité d’utilisateurs (en terme courant, « des bouchons »). Dans la pratique, d’autres facteurs peuvent influer sur le temps de transport, comme le type de véhicule utilisé, mais ignorons-les pour simplifier notre étude. Mathématiquement, on peut donc modéliser chacun des tronçons par une fonction qui prend en entrée la quantité d’usagers et qui donne en sortie le temps associé. La variable \(x\) de la fonction peut varier de \(0\) s’il n’y a pas d’usagers sur la route jusqu’à \(1\) quand tous les usagers du système sont sur ce tronçon (donc l’intervalle \([0,1]\) est l’espace de définition de la fonction).
On imagine que le tronçon A-B est constitué d’un dédale de rues dans une ville. Comme les rues sont étroites, il n’est pas aisé d’opérer des dépassements, de plus il y a beaucoup d’intersections dans la ville. Alors plus il y a de monde, plus l’impact de chacun sur la route est important. En termes mathématiques, la fonction de temps associée est convexe : elle augmente de plus en plus vite avec la congestion.
Dans notre cas, quand la ville est déserte le temps de trajet est très court, disons 3 minutes, mais si la ville est saturée alors le temps de trajet monte jusqu’à 20 minutes. Quand la situation est intermédiaire (avec 50% de saturation), le temps est de 7 minutes 30 secondes. On voit ici que la fonction de temps est bien convexe, car le passage de 0 à 50 % de saturation engendre une augmentation du temps de parcours de 4 minutes 30 secondes, mais que le passage de 50% à 100 % augmente le temps de parcours de 12 minutes 30.
Un exemple simple de fonction convexe est la fonction quadratique. Avec ces paramètres, la fonction quadratique correspondante est définie par \(f_\text{A-B}(x) = 3+x+16 x^2\) avec \(x\) la proportion d’utilisateurs sur ce tronçon. On vérifie que \(f_\text{A-B}(0) = 3\) correspond au temps de trajet quand la route est vide et que \(f_\text{A-B}(1) = 20\) correspond au temps quand tout le monde prend ce tronçon. Enfin \(f_\text{A-B}(0,5) = 7,5\) correspond au temps intermédiaire.
Une fonction quadratique est une fonction polynomiale (c’est-à-dire qui utilise des puissances de la variable x) du second degré (d’où le nom de quadratique, dérivé du latin « quadratus » qui signifie « carré »). Ce sont donc des fonctions du type \(f\) qui à tout \(x\) réel associe \(f(x) = a x^2 + b x + c\) avec \(a,b,c\) qui sont des nombres, les « paramètres » de la fonction. Par exemple, la fonction \(g\) qui à tout \(x\) réel associe la valeur \(3 x^2 + 5 x + 12\) est une fonction quadratique. Comme une fonction quadratique a 3 paramètres, alors elle est parfaitement définie par son passage en 3 valeurs.
De la même façon, le tronçon C-D est très sensible aux bouchons, avec un temps de trajet variant entre 2 minutes et 8,5 minutes et un temps intermédiaire de 4 minutes 30. La fonction quadratique correspondante est alors \(f_\text{C-D}(x)=2+3,5x+3 x^2\).
Inversement, dans notre exemple, le tronçon A-C est parfaitement insensible au temps car il s’agit d’une péniche qui relie les points A et C. Comme elle est de grande capacité et qu’il ne peut y avoir de bouchons sur notre rivière, le temps de traversée est constant et vaut 22 minutes. L’expression de la fonction de temps est donc \(f_\text{A-C}(x) = 22\). On parle de fonction constante.
Enfin le tronçon B-D est une portion de voie rapide, de type boulevard périphérique. Ce tronçon est sujet à la congestion mais de façon « linéaire » c’est-à-dire que l’impact de chaque utilisateur est le même. Dans notre exemple, quand la voie est libre, le temps de trajet est de 10 minutes. Quand la voie est parfaitement saturée, elle est de 12 minutes. La fonction associée est donc \(f_\text{B-D} = 10+2x\). On parle de fonction affine.
Les états d’équilibre
Nous avons donc maintenant les éléments nécessaires pour analyser notre système. Si l’on suppose que le système se répète, les utilisateurs et utilisatrices vont pouvoir essayer l’un ou l’autre des chemins pour apprendre progressivement celui qui est le plus rapide. C’est une méthode naturelle d’apprentissage chez les humains, mais elle est également très utilisée par les machines. C’est la philosophie de ce que l’on appelle « l’apprentissage par renforcement » : on essaye chaque choix possible avec une certaine probabilité, on mesure le résultat (ici le temps de parcours) et on adapte en diminuant progressivement les probabilités de faire des choix considérés comme mauvais et augmentant les probabilités des bons choix. L’utilisation des probabilités est très judicieuse ici. En effet, des aléas peuvent fausser notre mesure de la qualité de la route : par exemple, la météo, un accident, le passage du Tour de France ou tout autre élément extérieur… On dit que les mesures sont « bruitées ». Alors la « vraie » qualité de la route est connue en prenant plusieurs mesures que l’on moyenne ensuite. Le fait de prendre des décisions en utilisant des probabilités permet de ne pas écarter brusquement une décision qui est presque toujours bonne mais est apparue à un moment donné comme mauvaise. Ici l’apprentissage peut être long du fait que la performance mesurée dépend à la fois de nos propres choix et des choix faits par les autres usagers. Inversement, il peut être facilité dans la pratique par la technologie, notamment grâce aux informations de trafic de type GPS.
Pour l’heure, intéressons-nous seulement à l’état d’équilibre du système, c’est-à-dire la situation dans laquelle aucun utilisateur n’a intérêt à changer de choix de route. Un utilisateur voyant que le chemin qu’il a choisi est plus lent que l’autre aurait intérêt à changer de choix de route. De ce fait, à l’équilibre, les deux chemins ont le même temps de parcours. Pour trouver ce temps et les proportions de trafic correspondantes sur chacun des chemins considérés, il faut retourner aux équations.
Notons \(x\) la proportion d’usagers sur le chemin A-B-D. Alors la proportion d’usagers sur le chemin A-C-D vaut \(1-x\). Calculons le temps de trajet correspondant :
| \(\text{Temps_Trajet_Chemin}_\text{A-B-D}(x)\) | \(=\) | \(\text{Temps_Tronçon}_\text{A-B} + \text{Temps_Tronçon}_\text{B-D}\) |
| \(=\) | \(f_\text{A-B}(x) + f_\text{B-D}(x)\) | |
| \(=\) | \(3+x+16x^2+10+2x\) | |
| \(=\) | \(13 + 3 x + 16 x^2.\) |
De la même façon, nous avons
| \(\text{Temps_Trajet_Chemin}_\text{A-C-D}(x)\) | \(=\) | \(\text{Temps_Tronçon}_\text{A-C} + \text{Temps_Tronçon}_\text{C-D}\) |
| \(=\) | \(f_\text{A-C}(1-x) + f_\text{C-D}(1-x)\) | |
| \(=\) | \(22 + 2 + 3,5 (1 – x) + 3 (1 – x)^2.\) |
Après quelques lignes de calcul, nous obtenons :
\[ \text{Temps_Trajet_Chemin}_\text{A-C-D}(x) = 30,5 – 9,5 x + 3 x^2. \]
À l’équilibre, la proportion de trafic sur le chemin A-B-D est \(x\) qui est donc solution de l’équation
\[ \text{Temps_Trajet_Chemin}_\text{A-B-D}(x) = \text{Temps_Trajet_Chemin}_\text{A-C-D}(x).\]
Donc \(x\) est solution de \(13 + 3 x + 16 x^2 = 30,5 – 9,5 x + 3 x^2\), ce que l’on peut simplifier en \( 13 x^2 + 12,5 x – 17,5 = 0\). On reconnaît ici une équation polynomiale du second ordre que l’on peut résoudre avec les formules classiques, en calculant son discriminant \(\Delta = 12,5^2 + 4*13*17,5 = 1066,25\) et donc on obtient \[x = \frac{\sqrt{1066,25}-{12,5}} {26}\] soit environ \(0,775\). Donc, à l’équilibre, il y a environ \(77,5 \%\) des usagers qui utilisent le chemin A-B-D et \(22,5 \%\) qui choisissent le chemin A-C-D. En reportant ces proportions dans les équations, on voit que tous ont donc un temps de trajet d’environ 24,94 minutes soit 24 minutes et 56 secondes. On peut vérifier ce résultat et le comportement du système en manipulant les ascenseurs sur l’animation ci-dessous.
Voici de façon stylisée l’exemple considéré sur l’image précédente. Les utilisateurs peuvent utiliser soit le chemin bleu, soit le chemin rouge.
À côté de chaque « tronçon » la fonction de temps de trajet est représentée, en fonction du trafic. Le temps de passage est indiqué et aussi représenté par un niveau de gris (plus il est foncé, plus le temps est grand). Regardez les petits « ascenseurs » en bas à gauche. En déplaçant le curseur, on peut modifier la proportion de personnes sur chacun des chemins. Regardez bien à droite également les temps de trajet correspondants. À votre avis, si les gens choisissent systématiquement le chemin le plus court, à quel niveau de proportion est-ce que personne n’a aucun intérêt à changer de route ?
Supposons maintenant que l’on rajoute un tronçon de route entre les lieux B et C. Un tout petit tronçon qui correspond à un temps de 0,5 minutes. Le nouveau réseau est donc donné par ce nouveau schéma :
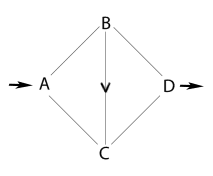
Figure 2
On peut trouver par le raisonnement le nouvel équilibre du système. Il y a désormais trois chemins possibles : A-B-D, A-C-D et A-B-C-D. Comparons leurs temps de parcours :
- Entre le chemin A-B-D et le chemin A-B-C-D, le début du parcours est le même. Il suffit donc de comparer le temps de passage B-D au temps de passage B-C-D. Sur B-D on sait que dans le meilleur des cas (quand il n’y a pas de bouchons) le passage dure 10 minutes. De plus, sur B-C on sait que dans tous les cas, le temps de passage est de 30 secondes. De même, dans le pire des cas, il faut 8,5 minutes pour effectuer le trajet C-D. Donc il faut au maximum 9 minutes pour effectuer le chemin B-C-D, ce qui est inférieur au temps de passage sur le tronçon B-D dans le meilleur des cas. Ainsi, pour un usager donné, le chemin A-B-D n’est jamais intéressant à prendre, quels que soient les choix des autres usagers.
- Comparons maintenant le chemin A-B-C-D et le chemin A-C-D. Dans ce cas, c’est la fin de parcours qui est la même. Il suffit donc de comparer le temps de passage sur A-B-C au temps de passage sur le tronçon A-C. Or, on sait que sur A-B-C le temps de passage est compris entre 3,5 minutes et 21 minutes alors que le temps de passage sur A-C est toujours de 22 minutes. Autrement dit, il n’est jamais intéressant de prendre le chemin A-C-D : quelles que soient les stratégies des utilisateurs, le chemin A-B-C-D lui sera préférable.
À partir de ce raisonnement, on en conclut qu’à l’équilibre, tous les usagers vont prendre le chemin A-B-C-D. Donc, leur temps de trajet sera, à tous, de :
\[ \text{Temps_Trajet} = f_\text{AB}(1) + f_\text{BC}(1) + f_\text{CD}(1) = 20 + 0,5 + 8,5 = \mathbf{29} \textbf{ minutes}. \]
On peut se convaincre de ce résultat grâce à la petite animation ci-dessous.
Voici maintenant le même exemple avec un tronçon supplémentaire entre les points B et C. Comme ce tronçon est à sens unique, cela rajoute un chemin supplémentaire : le chemin violet.
Comme dans l’animation précédente, les petits ascenseurs permettent de faire évoluer la proportion d’utilisateurs sur les différentes routes. Sur cette animation, nous avons fait le choix que le déplacement d’un ascenseur se reporte à part égale sur les deux autres. Ainsi par exemple, si la quantité d’usagers sur la route 1 augmente d’une quantité de 0.2 alors elle diminue de 0.1 sur chacun des chemins 2 et 3.
Selon vous, quel va être le nouvel état d’équilibre ? Quel est le temps de trajet subi par les usagers ?
Et patatras !
Et voilà, l’ajout du chemin supplémentaire a dégradé le temps de trajet de tous les usagers de plus de 4 minutes : le système « augmenté » est donc moins bon. Ce résultat est contre-intuitif du fait que la capacité de circulation est augmentée par l’ajout de routes. La dégradation des performances est uniquement la conséquence du comportement égoïste des usagers dans leurs choix d’actions. Cet exemple est particulièrement intéressant, car on peut voir qu’aucun usager n’aurait intérêt à « jouer collectif » : en effet, un utilisateur altruiste serait pénalisé par rapport aux autres, et comme on considère les densités d’utilisateurs, chaque automobiliste est infinitésimal (son impact est négligeable sur les autres), donc le « sacrifice » d’un seul utilisateur ne serait même pas bénéfique pour les autres.
On voit ici que la seule façon pour obtenir de bonnes performances dans le système augmenté serait que personne ne prenne le tronçon B-C. Cela peut se faire de deux façons : soit on fait appel à un législateur (qui va interdire le tronçon en question au nom du bien-être collectif), soit on autorise les utilisateurs à faire leur choix librement mais on augmente artificiellement les temps de parcours des tronçons en fonction de leur impact sur le bien-être total. Cette deuxième option revient à ajouter un ralentisseur (par exemple un dos d’âne) sur le tronçon B-C de sorte à le rendre moins intéressant pour les utilisateurs.
Et dans la vraie vie ?
Depuis les rues de nos villes…
On peut se poser la question de savoir si la topologie du réseau (c’est-à-dire la position des routes) et les fonctions de temps choisies dans cet exemple sont tellement pathologiques qu’il est improbable qu’elles se produisent dans les réseaux routiers actuels. En fait, les études mathématiques sur la caractérisation des structures des villes (le nombre de routes et leurs intersections) et des fonctions de temps mettent en relief la diversité des cas de paradoxes. De plus, à la faveur de travaux de rénovation dans les rues, plusieurs exemples réels ont été recensés. Parmi eux, le cas de la 42e rue de New York dont la fermeture a amélioré la circulation dans la ville a été fortement médiatisé. D’autres situations similaires ont été observées, notamment à Séoul, Londres et Stuttgart.
Dans cet article de presse (en anglais), le journaliste explique que la 42e rue de New York a été fermée le 22 avril 1990 pour effectuer des travaux de voirie. Cette rue étant connue pour être très congestionnée, les autorités ont anticipé une aggravation du niveau de congestion dans la ville, mais c’est tout le contraire qui a été observé. Ce qui est intéressant, c’est que cet article explique le scénario du paradoxe de Braess ainsi que des travaux consécutifs d’autres chercheurs. Il souligne notamment le fait que cette situation est très courante et précise que le commissaire aux transports, M. Riccio, lui-même docteur en ingénierie, s’intéresse aux modèles mathématiques sous-jacents pour améliorer la situation de congestion chronique de la ville de New York.
… jusqu’au monde numérique
Les chercheurs et chercheuses en informatique s’intéressent aux problématiques des paradoxes depuis les années quatre-vingt-dix. D’une part, l’étude des paradoxes est en soi un objet d’étude passionnant en optimisation et en algorithmie. Toute une branche de l’informatique s’intéresse au niveau de dégradation pouvant exister, ce que l’on appelle désormais le « prix de l’anarchie ». D’autres types de paradoxes similaires existent du fait de l’égoïsme des comportements : par exemple le fait de créer des alliances entre acteurs peut être néfaste, ou bien le fait d’avoir un meilleur niveau d’information que les autres.
D’autre part, depuis l’avènement des réseaux informatiques et des grandes structures de calcul partagées, plusieurs utilisateurs sont amenés à partager un ensemble de ressources communes. Comme dans l’exemple des routes, chacun des usagers peut prendre des décisions qui ont un impact sur les autres, donc des situations de paradoxes tels que celui des réseaux routiers apparaissent. Ici, les décisions ne sont plus alors prises par des humains mais par des algorithmes dans les machines. Chaque algorithme a pour objet d’optimiser ce que l’on appelle une « fonction d’utilité » qui représente le confort ou la « qualité de service » pour l’utilisateur.
Ainsi par exemple dans les réseaux de télécommunications, plusieurs utilisateurs échangent simultanément des données sur un média partagé. Les algorithmes situés dans les terminaux (téléphones, ordinateurs, capteurs, etc.) prennent en permanence des décisions pour optimiser la qualité du confort de l’utilisateur en termes de choix de routes, puissance et débit d’émission de données, niveaux de compressions, etc. De la même façon, les équipements réseaux peuvent appartenir à différents opérateurs interconnectés, chacun ayant sa fonction de confort propre.
Comme dans le cas du réseau fictif étudié, les opérateurs de ces systèmes partagés ont fortement intérêt à anticiper les situations paradoxales et à implanter des solutions : soit en ajoutant des contraintes au système pour empêcher certaines stratégies, via des réglementations ou contraintes collectives (appelées protocoles), soit en dégradant certaines performances pour dissuader les usagers de prendre certaines décisions. Cette deuxième approche s’appuie sur les travaux sur le « bien-être social », et notamment la « taxe pigouvienne » du nom de Arthur Cecil Pigou, économiste britannique. Car, utilisées à bon escient, les taxes peuvent être utiles pour inciter les gens à agir dans leur propre intérêt et perpétuer le « plus égale plus » !
Les animations HTML5/JS présentes dans cet article ont été réalisées par Ouest INSA, sous la coordination de l’autrice.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Corinne Touati
Chargée de recherche Inria en théorie des jeux.
Crédit : Photo © Inria / B. Fourrier
