Simulation numérique des mouvements de chevelure

Si l’animation de personnages virtuels a bénéficié de nettes avancées ces vingt dernières années, la modélisation de cheveux demeure en soi un problème de recherche scientifique difficile et encore assez peu exploré, que ce soit dans le domaine de l’informatique graphique, de la physique ou de la mécanique.

La difficulté provient avant tout de la complexité structurelle d’une chevelure. Une chevelure humaine est en effet un matériau hétérogène constitué d’environ 100 000 cheveux en interaction les uns avec les autres, chaque cheveu se présentant comme une tige partiellement translucide très fine et recouverte d’écailles. Or, contrairement à d’autres milieux déformables tels que les fluides, dont le mouvement est modélisé depuis près d’un siècle par les équations reconnues et validées de Navier-Stokes, la chevelure en tant que milieu déformable, ne bénéficie pour l’heure d’aucun modèle mécanique de référence équivalent. L’étude scientifique de ce matériau si particulier a été délaissée (du moins jusque dans les années 1980) du fait de l’absence d’enjeux économiques à cette époque.

Nous proposons un nouveau modèle mécanique du cheveu sous forme d’hélices par morceaux, fruit d’une collaboration entre équipes de recherches de différentes disciplines.

Méthodologie de la modélisation

Chacun des cheveux composant une chevelure est un cylindre très fin (dont le diamètre est de l’ordre du dixième de millimètre), pratiquement inextensible, et pouvant présenter une forme naturelle très variable selon l’origine ethnique de la personne (chevelure lisse, ondulée, bouclée, frisée, etc.). Ces trois éléments — finesse, inextensibilité et forme naturelle d’une fibre capillaire — ont un impact direct sur le mouvement d’une masse de cheveux, caractérisé par des déformations non-linéaires en courbure et en torsion.

Dans un premier temps, il a donc fallu modéliser finement la dynamique d’une fibre individuelle, en préalable à l’étude de l’élasticité d’une chevelure complète.

Par ailleurs, chaque fibre est soumise à de nombreux contacts avec les fibres voisines. Ces entremêlements donnent naissance à des comportements collectifs caractéristiques au sein de la chevelure : par exemple, les cheveux frisés se regroupent souvent en un ensemble de mèches distinctes. Or, simuler 100 000 fibres individuelles et traiter tous les contacts simultanés se produisant entre les fibres engendrerait des coûts de calcul insurmontables. Même en utilisant les plus simples et les moins coûteux des modèles de fibres et d’interaction, il faudrait des jours voire des semaines de calcul pour obtenir ne serait-ce que quelques secondes d’animation pour une chevelure complète, en utilisant un PC standard.

Une alternative consiste à ne simuler physiquement que quelques centaines de cheveux individuels répartis uniformément dans la chevelure, chacun de ces cheveux servant alors de guide pour le mouvement d’un ensemble de fibres regroupées autour de chacun d’eux. Cette stratégie permet de réduire considérablement la complexité du problème, et rend possible la simulation d’une chevelure complète. La principale difficulté consiste alors à déduire de manière cohérente le mouvement et la forme de la totalité des cheveux composant une chevelure, à partir de quelques centaines de fibres individuelles données.

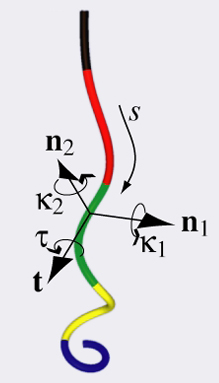
Modèle mécanique discret de Super-Hélice.
Chacun de ces 5 morceaux (de couleur différente) est une hélice circulaire parfaite et se raccorde de manière lisse aux morceaux adjacents.

Modélisation mécanique d’une fibre individuelle

En mécanique, les déformations des tiges élastiques et inextensibles sont décrites par les équations de Kirchhoff. Ces équations, bien que formulées dans le cadre de l’élasticité linéaire, régie par la loi de Hooke, sont non-linéaires et permettent de décrire des changements importants de formes à partir de la configuration d’une tige au repos. Reposant sur des bases mécaniques bien établies, les équations de Kirchhoff tiennent compte de tous les modes de déformations observés sur les cheveux réels, dans nos conditions d’étude (courbure et torsion significatives, élongation négligeable). Tous les paramètres intervenant dans ces équations sont en outre reliés à des propriétés simples du cheveu telles que sa frisure ou la forme elliptique de sa section. Pour toutes ces raisons, les équations de Kirchhoff apparaissent comme un modèle beaucoup plus puissant et pertinent que les modèles précédemment utilisés pour parvenir à une simulation réaliste des cheveux.

Cependant, ces équations, qui dépendent des deux variables continues que sont l’espace et le temps, n’admettent généralement pas de solution exacte, et leur résolution à l’aide d’un ordinateur soulève d’importantes difficultés numériques. En effet, la présence dans les équations de Kirchhoff de termes non-linéaires, ainsi que de dérivées spatiales de haut degré, rend l’échantillonnage spatial délicat : les méthodes numériques classiques (différences finies, éléments finis) ont du mal à converger sur un domaine spatial satisfaisant, générant alors d’importantes instabilités lors de la simulation.

Pour faire face à ce problème, une idée consiste à construire de nouvelles équations mécaniques pour une tige déjà échantillonnée en espace, et ce, en s’inspirant des équations continues de Kirchhoff. Ainsi, en subdivisant une tige en plusieurs morceaux, et en supposant que chaque morceau de la tige est caractérisé par des paramètres de déformation (en courbure et en torsion) constants sur toute la longueur du morceau, on peut écrire de nouvelles équations mécaniques, qui ne dépendent cette fois-ci plus que de la variable temps, tous les termes en espace pouvant se calculer de manière exacte. C’est ce que nous avons appelé modèle de Super-Hélice, car chacun des morceaux composant la tige — caractérisé par une courbure et une torsion constantes — se révèle avoir la forme d’une hélice circulaire parfaite.

Chaque élément de tige peut également prendre une forme en arc de cercle ou en segment de droite, ces deux formes étant mathématiquement des cas particuliers d’hélice. La structure animée est donc composée de morceaux d’hélices raccordés entre eux de manière lisse. Pour calculer l’évolution de ce modèle au cours du temps, il reste alors à échantillonner numériquement la seule variable de temps intervenant dans les équations mécaniques, en utilisant un schéma d’intégration numérique implicite, garantissant une convergence sur un bon domaine spatial pour le modèle. Il en résulte un modèle de tige dynamique très stable, et capable de subir des déformations spatiales relativement importantes.

Un autre grand intérêt de cette méthode résulte de l’ajustement possible du nombre de degrés de liberté (c’est-à-dire le nombre de morceaux d’hélices choisi pour représenter la tige) à la demande de l’utilisateur, en fonction du compromis désiré entre précision et efficacité. Ainsi, pour des applications exigeant une bonne précision du modèle (simulation chirurgicale d’un fil de suture par exemple), on simulera une tige composée d’une quinzaine de morceaux d’hélice, tandis que pour celles nécessitant de bonnes performances en temps de calcul (jeu vidéo par exemple), on pourra volontairement « dégrader » le système pour ne conserver que quelques modes essentiels de déformation (quatre ou cinq morceaux d’hélice), et réduire les coûts de calcul tout en maintenant des résultats visuels satisfaisants.

Génération d’une chevelure complète

Comme évoqué précédemment, il n’est pas raisonnable de simuler individuellement les 100 000 cheveux composant une chevelure complète. Aussi, notre méthode consiste-t-elle à animer seulement quelques centaines de Super-Hélices, chacune de ces Super-Hélices servant de « cheveu guide » pour une mèche de cheveux. Il s’agit alors, pour l’animation d’une chevelure complète, de tenir compte de toutes les forces s’exerçant sur chacun des cheveux guides, et en particulier des forces de contacts (interactions cheveu/cheveu, mèche/mèche et mèche/corps du personnage), puis de générer l’ensemble des cheveux composant la chevelure à partir du mouvement des guides, pour la visualisation finale.

Interactions entre groupes de cheveux

Les interactions entre cheveux sont calculées à deux niveaux différents. Dans un premier temps, nous tenons compte des frottements de cheveu à cheveu se produisant au sein de chaque mèche, en ajustant un paramètre de frottement interne propre à la Super-Hélice servant de guide à cette mèche. Plus ce paramètre est élevé, et moins la Super-Hélice est susceptible de se déformer au cours du mouvement. Ainsi, pour une mèche emmêlée, soumise à de nombreux contacts « bloquants » entre cheveux, on choisira un frottement interne assez important. A contrario, pour une mèche très « disciplinée » (mèche lisse ou mèche bouclée, dans laquelle les cheveux sont parfaitement alignés), on choisira un frottement interne équivalent assez faible, permettant de restaurer la « nervosité » dynamique caractéristique d’une telle mèche.

Dans un second temps, nous traitons les interactions entre mèches en examinant le comportement dynamique des cheveux guides, et en le corrigeant dans le cas où le mouvement engendrerait des interpénétrations de mèches. Pour ce faire, il faut d’abord détecter les collisions possibles, en comparant la distance entre deux cheveux guides à l’épaisseur des mèches correspondantes en ce même endroit. Si la distance entre les cheveux guides à un instant donné est inférieure à la somme des épaisseurs des deux mèches correspondantes, cela signifie qu’il y a interpénétration. Cette opération de détection, habituellement coûteuse — car l’on teste toutes les paires de cheveux directeurs possibles, et ce pour des points d’échantillonnage suffisamment denses pour chaque cheveu — est ici effectuée de manière efficace en exploitant la cohérence temporelle du phénomène : à un pas de temps donné, la configuration des cheveux directeurs est très similaire à la configuration au pas de temps précédent. Cette constatation nous permet, au lieu de faire à chaque pas de temps une recherche exhaustive de toutes les combinaisons possibles, de réaliser un suivi de quelques paires de points les plus proches entre cheveux guides. Il suffit de faire glisser d’un pas de temps à l’autre ces paires de points le long des cheveux guides, de manière à disposer à chaque instant de la paire de distance minimale entre deux cheveux directeurs donnés. Lorsqu’une collision est détectée, on la traite alors en insérant des forces de pénalité, qui se chargeront de repousser les mèches l’une de l’autre au pas de temps suivant, de manière à annuler l’interpénétration. Nous intégrons également une composante de frottement tangentiel visqueux à ces forces, traduisant la résistance qu’offrent les mèches à glisser l’une sur l’autre. Ces frottements sont dits visqueux parce qu’ils sont liés à la viscosité des sécrétions à la surface des cheveux. De tels frottements augmentent proportionnellement à la vitesse tangentielle des cheveux, c’est-à-dire la vitesse de glissement d’un cheveu le long de l’autre. Les interactions entre les mèches de cheveux et le corps du personnage sont traitées de manière similaire, en approchant la forme géométrique du corps par un ensemble de sphères de collision.

Habillage géométrique

Une fois le modèle des cheveux guides élaboré, prenant en compte tous les types d’interaction évoqués précédemment, il s’agit de reconstruire l’ensemble des cheveux constituant la chevelure à partir de cette centaine de cheveux guides. Ce processus appelé « habillage géométrique » permet d’obtenir une visualisation fidèle à la réalité de la chevelure complète. Notons qu’en pratique, la reconstruction de quelques milliers de courbes à partir des cheveux guides suffit largement à représenter fidèlement une chevelure complète, pour peu que chacune de ces courbes soit un peu plus épaisse qu’un vrai cheveu (et représente en fait un petit groupe de cheveux collés les uns aux autres).

La question posée est alors la suivante : comment, à partir d’une centaine de cheveux guides, caractérisés par un degré de frisure commun (cheveux lisses, ondulés, frisés, etc.) pouvons-nous en déduire plusieurs milliers de cheveux (appelés cheveux cibles), tout en préservant le type ethnique caractéristique de la chevelure ?

Algorithme semi-interpolant pour la génération de la géométrie finale des cheveux à partir de trois cheveux guides.
a) les cheveux sont interpolés depuis les pointes jusqu’aux racines ;
b) les cheveux sont interpolés près des racines, mais pas près des pointes où des mèches distinctes apparaissent ;
c) aucune interpolation, les cheveux restent groupés autour de leur cheveu guide principal, d’où l’apparition de mèches disjointes ;
d) l’interpolation à travers l’épaule droite du personnage est évitée grâce au critère de distance maximale entre les pointes des cheveux guides.

L’observation de chevelures réelles fournit quelques éléments de réponse : on peut par exemple remarquer que les chevelures très lisses (asiatiques notamment) présentent souvent un aspect très continu, tandis que les cheveux bouclés ont davantage tendance à former des mèches bien séparées. Par ailleurs, les chevelures réelles ondulées ont généralement un aspect lisse et continu près du cuir chevelu, tandis que les pointes se regroupent en mèches séparées.

Pour synthétiser cette grande variété de formes, un modèle d’habillage semi-interpolant est élaboré. Il constitue en fait un modèle unifié des deux approches classiques d’habillage de chevelure qui représentent traditionnellement la chevelure soit comme un ensemble de mèches bien séparées, soit au contraire comme un milieu continu. Le principe de cette approche consiste à faire une représentation géométrique des cheveux cibles à partir des cheveux guides en réglant l’influence (ou le poids) de chaque cheveu guide sur la position des cheveux cibles dessinés. Si un cheveu guide donné a un poids prépondérant sur chaque cheveu cible, alors l’ensemble des cheveux cibles ainsi représentés restera groupé autour de ce cheveu guide, et ne sera pas influencé par les autres cheveux guides pendant l’animation (ce qui correspondra au cas des mèches séparées). Si, au contraire, les influences des différents cheveux guides sur chaque cheveu cible sont équilibrées, alors le paquet de cheveux cibles prendra l’apparence, au cours de l’animation, d’un continuum entre les différents cheveux guides (cas d’une chevelure lisse et homogène). Un critère sur la distance maximale tolérée entre les extrémités libres des cheveux cibles et des cheveux guides permet de rompre cette continuité lorsque les cheveux guides s’éloignent trop les uns des autres. De plus, le niveau d’interpolation souhaité peut être défini en chaque point de la chevelure, depuis les racines vers les pointes, offrant la possibilité d’obtenir toutes les représentations intermédiaires entre interpolation complète (milieu continu) et aucune interpolation (mèches séparées). Ce paramètre, réglable interactivement, permet ainsi à un utilisateur (infographiste par exemple) de contrôler lui-même l’apparence désirée, en fonction du degré de frisure de la chevelure, de critères esthétiques, etc.

Quelques résultats et validations

Validations expérimentales
À gauche : mise en évidence du phénomène de torsion sur une mèche légèrement ondulée, lors d’un mouvement oscillatoire de gauche à droite.
À droite : comparaison entre une chevelure complète réelle et le modèle numérique, sur un mouvement rapide de rotation de la tête autour de l’axe vertical.

Le modèle dynamique de cheveux ainsi élaboré a été confronté à la réalité en comparant le comportement dynamique d’une mèche de cheveux réels à celui obtenu par le modèle de synthèse, pour un même type de mouvement. Pour que la comparaison soit la plus pertinente possible, les paramètres du modèle ont été réglés de manière à ce qu’ils correspondent au mieux aux paramètres de la mèche de cheveux réelle : tout d’abord en mesurant au microscope un certain nombre de paramètres physiques et géométriques des fibres réelles (rayon moyen, excentricité moyenne de la section elliptique, module d’élasticité, etc.), et en évaluant le degré de frisure des cheveux réels (courbure et torsion naturelles moyennes), puis en injectant directement ces paramètres en entrée du modèle de Super-Hélice, utilisé comme cheveu guide pour la simulation de la mèche virtuelle. Seuls deux paramètres du modèle n’étaient pas mesurables directement : le paramètre de frottement interne de la mèche, et le coefficient de frottement air/cheveux. Afin d’obtenir une évaluation de ces paramètres, un protocole expérimental a été mis au point, permettant de dissocier l’effet de ces deux paramètres et de donner une estimation plausible pour chacun d’entre eux : le frottement interne, sensible aux déformations internes de la mèche, est d’abord estimé par ajustement sur un mouvement oscillatoire vertical de la mèche ; une fois ce paramètre ajusté, une seconde expérience consistant en un léger mouvement oscillatoire horizontal de la mèche (pour laquelle les déformations internes sont négligeables) sert à ajuster le coefficient de frottement air/cheveux, par exemple en calant le temps d’amortissement de la simulation sur le réel.

La technologie de simulation de chevelures que nous avons mise au point en collaboration avec les équipes de recherche de L’Oréal et grâce à leurs connaissances sur les propriétés physiques des cheveux allie réalisme physique et efficacité en temps de calcul. Le modèle intéresse aussi bien les professionnels du secteur du loisir, que ce soit pour la production de films d’animation 3D ou les jeux vidéo, que la cosmétique pour la mise au point de futurs soins capillaires.