Sonder l’invisible, du séisme au modèle

Grâce aux simulations numériques, on peut aujourd’hui déterminer les régions les plus exposées à un risque de tremblement de terre, afin d’orienter le choix des emplacements les plus appropriés à la construction d’habitations. Ces simulations sont également essentielles après un premier tremblement de terre, pour estimer les différentes répliques possibles et installer les populations réfugiées dans des endroits plus sûrs. Enfin, la reproduction de tremblements de terre passés fournit des informations sur les mécanismes à l’origine des séismes ainsi que sur la composition du globe terrestre. C’est dans le but de simuler des tremblements de terre qu’a été réalisé un logiciel spécifique, appelé SPECFEM.

Visionner la vidéo – Durée : 04 min 59 s.

Qu’est-ce qu’un tremblement de terre ?

Un séisme, ou tremblement de terre, résulte de la libération brusque d’énergie accumulée par les contraintes exercées sur les roches. La rupture des roches en surface génère une ou plusieurs failles. Le lieu de cette rupture en profondeur se nomme le foyer. Environ cent mille séismes sont enregistrés par an sur le globe, à l’aide de réseaux de sismographes permettant de détecter les ondes sismiques à plusieurs milliers de kilomètres du foyer sismique. La puissance d’un tremblement de terre peut être quantifiée par sa magnitude, fonction logarithmique introduite par le sismologue Francis Richter en 1935. Les séismes les plus fréquents et les plus dévastateurs sont généralement d’origine tectonique. Des séismes plus rares sont dus à la dynamique des volcans ou liés à des activités humaines. Lors d’un séisme, les ondes ne se propagent pas de la même façon dans toutes les directions. En effet, suivant la composition du milieu rencontré (argile, calcaire, etc.), la vitesse de propagation des ondes ainsi que leur atténuation peuvent fortement varier. De plus, des obstacles naturels comme les montagnes peuvent s’opposer à la propagation des ondes et les réfléchir. Il peut alors arriver que les ondes soient piégées entre deux massifs montagneux et soient réfléchies plusieurs fois avant que leur énergie ne décroisse. On comprend donc aisément que certaines régions (par exemple celles protégées de l’épicentre par une montagne) vont être relativement épargnées par les secousses sismiques alors que d’autres (celles situées entre l’épicentre et une montagne) vont subir d’importants dégâts. Les ondes de surface (ondes de Rayleigh ou de Love) sont guidées par la surface de la Terre et se propagent plus lentement que les ondes de volume (les ondes P ou de compression et les ondes S ou de cisaillement plus lentes que les ondes P) mais elles ont de plus fortes amplitudes. En général, ce sont les ondes de surface qui produisent les destructions les plus importantes. Lorsqu’un décrochement de faille se produit, l’énergie accumulée par la déformation élastique des roches puis le glissement qui s’ensuit est brusquement relâchée. Cette dissipation d’énergie liée au relâchement se fait par paliers, jusqu’à ce que le système de failles parvienne à un équilibre. De ce fait, un tremblement de terre est rarement isolé. Des répliques ont souvent lieu après une secousse principale, sur des échelles de temps de quelques minutes à un an. Ces répliques peuvent avoir des magnitudes plus importantes que la secousse principale, mais ce n’est généralement pas le cas. Elles ont le plus souvent une puissance moindre, qui s’atténue au cours du processus de relâchement par paliers. La force de ces répliques dépend de l’énergie emmagasinée par la faille au cours de temps. Pour schématiser, les tremblements de terre les moins destructeurs sont ceux qui ont vu leur énergie se dissiper peu à peu par plusieurs tremblements (ou dislocations de faille) de faible ou moyenne puissance. Il vaut donc mieux subir plusieurs tremblements, afin que l’énergie se relâche de manière lisse au cours du temps, qu’un plus petit nombre de tremblements de terre qui auraient vu le réseau de failles local emmagasiner trop d’énergie au cours du temps (plusieurs années, voire dizaines d’années) avant de casser.

Pourquoi simuler des tremblements de terre ?

Le rôle des simulations numériques n’est pas de prédire quand et où aura lieu un tremblement de terre, mais de déterminer la force et la trajectoire des ondes en fonction de l’endroit précis où il a lieu. Comme dit précédemment, toutes les zones ne sont pas exposées de la même façon. Il est important de connaître les zones les moins exposées afin de prévoir la construction de logements ou un meilleur aménagement du territoire. De même, il est crucial pour les autorités de savoir où installer les populations victimes d’un séisme pour les protéger des répliques. Les simulations numériques sont également utilisées pour reproduire des tremblements de terre passés. En comparant les résultats obtenus par la simulation avec ceux enregistrés par les sismographes, on peut améliorer les modèles de propagation des ondes, mais également obtenir des informations sur la composition des roches traversées par le séisme. La reproduction de ces tremblements de terre permet aussi de savoir comment les failles ont cassé, ce qui est un élément très important pour la détermination d’éventuelles répliques. Les simulations peuvent être réalisées sur l’ensemble du globe terrestre, on parle alors de simulation globale, ou sur une région limitée bien définie, on parle alors de simulation locale.

Comment simuler des tremblements de terre ?

Le modèle

Pour simuler les séismes, il faut d’abord avoir une bonne connaissance des caractéristiques des tremblements de terre ayant eu lieu, en particulier de la localisation spatiale des séismes. Ceci,
 conjugué à un bon modèle du sous-sol, indiquant les densités et les vitesses de propagation des ondes sismiques, permet de décrire la source du tremblement de terre (c’est-à-dire les failles ayant décroché) et le milieu dans lequel vont se propager les ondes, dans le volume et en surface. On obtient alors des équations qui modélisent la propagation des ondes émises par la source à travers le sous-sol. Il existe différents modèles de propagation des ondes. Le modèle le plus simple, dit modèle des ondes acoustiques, permet de simuler la propagation des ondes dans un fluide, par exemple la propagation du son dans l’air et dans l’eau. Le modèle des ondes élastiques, qui permet de simuler la propagation des ondes dans les solides, est un peu plus compliqué, mais plus proche de la réalité. Pour améliorer encore ce modèle, on peut y ajouter de la dissipation, qui permet de simuler l’amortissement des ondes dans le sous-sol. On peut également prendre en compte la porosité des roches, c’est-à-dire le fait que les roches sont des solides percés de trous minuscules contenant des fluides (eau, pétrole…). Tous ces modèles sont définis à la fois en espace et en temps. Que l’on fasse des simulations globales ou locales, le modèle considéré à l’intérieur du domaine de calcul reste le même. Cependant, pour faire des simulations locales, il faut également définir des conditions particulières aux bornes du domaine de calcul, qui permettent aux ondes de sortir du domaine sans être réfléchies.

© Inria / Magique 3D.

La première animation ci-dessus à gauche représente un exemple de simulation locale sans conditions particulières. On voit que les ondes sont complètement réfléchies à la frontière du domaine. Sur la deuxième animation, au centre, on a imposé une condition particulière qui permet aux ondes de sortir du domaine de calcul. On observe néanmoins quelques réflexions parasites. Celles-ci sont dues au fait que la condition utilisée n’est pas très précise. D’autres conditions, plus précises mais plus difficiles à mettre en œuvre, permettent d’obtenir de meilleurs résultats. Une autre méthode consiste à entourer le domaine de calcul par un milieu artificiel où les ondes sont absorbées (voir la troisième animation, à droite). Cette technique est très efficace, mais elle engendre des coûts de calcul légèrement plus élevés, car il faut prendre en compte un milieu supplémentaire.

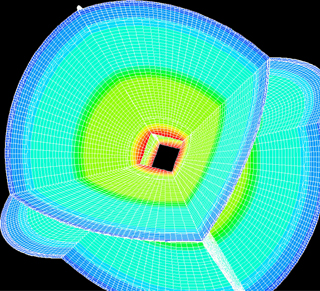
Maillage hexaédrique de la Terre. © Inria / Magique 3D.

La discrétisation du modèle

Le modèle que nous obtenons est défini sur l’ensemble de la Terre, c’est-à-dire pour une infinité de points. Or, un ordinateur ne peut traiter qu’un nombre fini de points. Il faut donc effectuer ce qu’on appelle une discrétisation, ou un maillage, de la Terre : on découpe la Terre en un certain nombre d’éléments, comme représenté sur la figure ci-contre. Il ne reste plus qu’à calculer la solution sur chacun de ces éléments. La solution calculée est alors une approximation de la solution exacte, qui sera d’autant plus précise que le nombre d’éléments sera élevé.

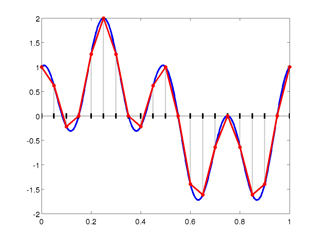
Ce phénomène peut être illustré très simplement en dimension 1. Sur la première figure ci-contre, nous avons représenté une courbe sur une longueur de 1 m (courbe bleue). Nous avons découpé l’intervalle en segments de 0,1 m et nous avons approché la courbe par des morceaux de droite (courbe rouge). Il est évident sur cette figure que la solution exacte est très bien approchée aux extrémités de chaque segment, mais que la courbe rouge est très différente de la courbe bleue.

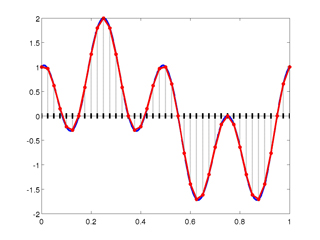
En choisissant des segments de plus petite taille (0,05 m), les deux courbes sont beaucoup plus proches (voir la deuxième figure ci-contre). Il est également possible d’obtenir une meilleure représentation de la solution en utilisant des polynômes au lieu de droites. Cette technique nécessite d’introduire des points supplémentaires sur chaque segment. En effet, les droites sont définies par des fonctions de type f(x)= a × x + b et il suffit de deux points pour déterminer les deux inconnues a et b.

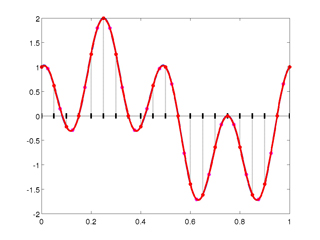
Si on choisit des polynômes de degré 2, qui sont des fonctions de type a × x² + b × x + c, il y a trois inconnues à déterminer (a, b et c) et il faut donc trois points sur chaque segment. En général, on considère un troisième point au milieu du segment et on détermine alors l’unique polynôme de degré 2 qui coïncide avec la courbe sur les extrémités et au milieu du segment. Nous illustrons cette démarche sur la troisième figure ci-contre. Nous avons ici considéré des segments de longueur 0,1 m. En comparant les solutions approchées de la première et de la troisième figure, on voit clairement que le fait d’utiliser des polynômes de degré plus élevé améliore le calcul. En résumé, plus le nombre de segments est grand et plus le degré des polynômes est élevé, plus la solution sera précise. En contrepartie, les nombre de points à considérer, et donc la charge de calcul seront beaucoup plus grands. Il faut donc trouver un compromis entre la précision de la solution et le coût du calcul. Cette illustration en dimension 1 se généralise sans difficulté au cas de la dimension 3 qui nous intéresse pour les problèmes géophysiques (mais la représentation graphique du phénomène est plus délicate). Une fois le problème de la discrétisation en espace résolu, il faut considérer la discrétisation en temps. En effet, les modèles que nous considérons sont définis en tout point de l’espace mais également du temps. L’idée est à nouveau de découper l’intervalle temporel en petits segments. La différence est qu’on calcule la solution à un instant donné uniquement à partir des solutions calculées aux instants précédents, alors que pour la discrétisation en espace, la solution en un point dépend de ce qui se passe à gauche et à droite de ce point.

Le calcul parallèle

Grille de calcul. © INRIA / Photo Kaksonen.

Même en utilisant un maillage, le nombre d’éléments à traiter est trop important pour un seul ordinateur. La solution est d’utiliser un très grand nombre de processeurs (une grille de calcul) et de donner à chacun un petit morceau du calcul, c’est-à-dire un petit nombre d’éléments à traiter. Pour accélérer le calcul, on s’oriente maintenant vers l’utilisation de processeurs de cartes graphiques (comme ceux qui gèrent l’affichage sur votre ordinateur) qui s’avèrent mieux adaptés au calcul scientifique.