
Systèmes dynamiques et équations différentielles
« Élémentaire » ne veut pas dire facile à comprendre.
« Élémentaire » veut dire qu’on n’a pas besoin de connaître
grand’chose à l’avance pour […] comprendre.
Richard Feynman, Le mouvement des planètes autour du soleil,
cours du 13 mars 1964, Caltech
Une masselotte accrochée à un ressort, un pendule, ou un circuit électrique connectant condensateur et bobine, constituent des exemples de systèmes dynamiques bien connus, car étudiés au lycée. Mais les exemples abondent tout autant en chimie, en biologie ou en économie.
Un système dynamique est en effet un ensemble d’entités en interaction. Du fait même de ces interactions, la valeur de grandeurs attachées à ces entités évolue dans le temps. C’est en étudiant l’évolution de ces valeurs que l’on cherche à comprendre et à prédire le comportement de ces systèmes. Cela repose sur leur représentation mathématique à l’aide d’équations différentielles.
Dans l’exemple de la masselotte accrochée à un ressort, la grandeur dont la valeur évolue peut être la distance de son centre de gravité à sa position au repos. Dans un circuit électrique, ce seront des tensions ou des intensités ; en chimie, les concentrations des molécules en présence ; en biologie, les effectifs ou les densités de populations au sein d’un écosystème, mais aussi, au niveau cellulaire, les concentrations de produits de gènes ; en économie, des montants de capital ou de travail, ou encore des flux financiers.
À chacune de ces grandeurs, il est possible d’associer une variable dont la valeur change en fonction du temps. On nommera ainsi x(t) la distance de la masselotte à sa position d’équilibre, U(t) la tension aux bornes d’un condensateur, CO2(t) la concentration en gaz carbonique, N(t) le nombre de proies et P(t) le nombre de prédateurs, K(t) le capital et L(t) le travail, etc.
Une valeur n’a de sens que si l’unité dans laquelle elle est exprimée est précisée. Pour les grandeurs physiques, le choix de l’unité est imposé par le système international (SI). Ainsi, la distance x(t) doit-elle être exprimée en mètres et la tension U(t) en volts. Mais des entorses au système sont fréquentes. Ainsi, la concentration en CO2 devrait être exprimée en moles par dm3, soit mol/dm3, ou encore mol . dm-3. Or on la trouve le plus souvent exprimée en ppm (partie par million), voire en pourcentage, qui sont des proportions et donc des nombres sans dimension, auxquels aucune unité n’est associée. Plus simplement, les nombres de proies et de prédateurs N(t) et P(t) sont des effectifs, sans dimension. Parfois, le choix même de l’unité est problématique, lorsque la grandeur elle-même est délicate à définir. C’est le cas pour le capital K(t), alors que le travail L(t) s’exprime assez naturellement en heures.
Disposant de connaissances sur les interactions entre les diverses entités qui composent le système étudié, est-il possible de comprendre comment les valeurs de ces variables évoluent dans le temps, et par là-même, de comprendre le comportement du système ?
La solution à cette interrogation passe par les équations différentielles. Les x(t), U(t) et autres N(t) peuvent être vues comme des fonctions de la variable indépendante t, le temps. Cette variable est indépendante car sa valeur ne dépend d’aucune autre variable. Si, par analyse du système, il est possible d’écrire une expression mathématique liant la fonction x, qui à t associe x(t), et ses dérivées – première x’(t), seconde x”(t), etc. – on obtient une équation dite « différentielle ». C’est la solution de cette équation différentielle qui, si elle existe, déterminera la fonction x(t) jusque-là inconnue. Et si l’expression mathématique de la fonction x(t) est disponible, alors les valeurs de la variable x peuvent être obtenues pour toute valeur de t. Il est alors possible d’étudier le comportement du système dynamique, du moins à travers l’évolution de la variable x.
Comme x est une fonction de la seule variable t, le temps, c’est sans risque d’ambigüité qu’on écrira indifféremment x ou x(t). De même, on écrira sa dérivée première sous la forme explicite dx(t)/dt, ou plus simplement dx/dt, ou encore x’(t) ou x’.
La où les équations différentielles constituent un modèle du système, la construction d’un modèle constitue le processus de modélisation.
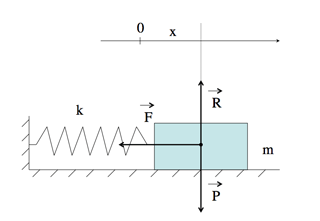
Système masselotte-ressort.
La masselotte de masse m est supposée glisser sans frottement. \(\vec{R}\) est la réaction du support, égale au poids \(\vec{P}\). La masselotte n’est donc soumise qu’à la seule force de rappel \(\vec{F}\), proportionnelle à la distance x à sa position à l’équilibre (où \(\vec{F}\) est nulle).
Les exposés de physique élémentaire peuvent laisser penser que ce processus de modélisation est systématique et en fait assez simple. S’agissant ainsi du système masselotte – ressort, il est vrai qu’il suffit d’écrire que la résultante des forces qui s’appliquent sur la masse, plus exactement sur son centre de gravité, se réduit à la force de rappel du ressort \(\vec{F}\). Cette résultante est égale, selon l’expression mathématique de la deuxième loi de Newton, au produit de la masse m par son accélération. Or, l’accélération est la dérivée seconde de la distance x(t), notée x”(t). En effet, l’accélération est la dérivée de la vitesse et la vitesse est la dérivée première de la distance.
La vitesse d’une automobile est sans doute la fonction dérivée la plus connue et la plus intuitive. À tout moment, le compteur de la voiture informe son conducteur de sa vitesse en km/h. Si le compteur affiche 75 km/h, cela signifie que, si le conducteur maintient très exactement cette vitesse pendant une heure, il aura parcouru 75 km. Bien entendu, cette vitesse varie en fonction de multiples facteurs : profil de la route, position du pied sur l’accélérateur, vitesse et direction du vent, etc. À tout instant, le compteur affiche ainsi la vitesse instantanée, mesurée cependant en kilomètres par heure. Plus la vitesse est élevée, plus la voiture parcourt une distance élevée pendant un même intervalle de temps, qu’il faut prendre suffisamment petit pour que la vitesse puisse y être considérée constante. La vitesse est ainsi la dérivée de la distance.
L’accélération est le taux de variation instantanée de la vitesse. Une accélération positive indique une vitesse croissante, une accélération nulle indique une vitesse constante et une accélération négative indique une vitesse décroissante. L’accélération est la dérivée de la vitesse, et donc la dérivée seconde de la distance. Elle s’exprime en (km/h) / h, autrement dit en km / h2, ou encore km . h-2.
Soit x(t) la distance parcourue depuis le début du déplacement, v(t) la vitesse à l’instant t et γ(t) l’accélération.
La vitesse v est la dérivée de la distance :
dx(t)/dt = v(t)
L’accélération γ est la dérivée de la vitesse v :
dv(t)/dt = γ(t)
On peut donc écrire :
\[\frac{dv}{dt} = \frac{d(\dfrac{dx}{dt})}{dt} = \frac {d^2x}{dt^2} = \gamma \]
qui se note aussi x”(t) = γ(t) ou encore x” = γ.
L’accélération est à tout moment égale à la dérivée seconde de la distance.
Par ailleurs, la force de rappel peut être considérée, sous certaines hypothèses restrictives, comme étant proportionnelle à l’allongement x(t) du ressort (loi de Hooke). On obtient donc immédiatement : m x”(t) = – k x(t) où k est la constante de raideur du ressort.
L’exposé se poursuit en expliquant comment l’équation différentielle m x”(t) = – k x(t) admet comme solution la fonction x(t) = A cos (ω t + φ) qui rend finalement compte du comportement oscillatoire périodique du système étudié. A est l’amplitude des oscillations, exprimée dans la même unité que x(t) ; ω est la pulsation, exprimée en radian par seconde (soit radian / s, ou encore radian . s-1) et elle est égale à √ (k / m) ; φ est la phase. Si le temps 0 est pris au moment où l’élongation est maximale et égale à x0, on a A = x0 et φ = 0 et x (t) = x0 cos (ω t).
La modélisation des systèmes physiques simples se ramène ainsi, de par l’existence de lois déjà disponibles sous forme mathématique, à une mise en équations directe. L’objet résultant, ici une équation différentielle du deuxième ordre, est quasiment donné par la définition du système et les lois qui le régissent.
Mise en équation ou modélisation ?
Or, il est peu fréquent que l’obtention d’un modèle mathématique d’un système soit aussi immédiate. En fait, la démarche de modélisation d’un système est essentiellement itérative et implique de nombreux choix, guidés par les objectifs de la modélisation. La toute première question est « Quel est le système ? » : Quelles en sont les entités constitutives ? Quelles sont les grandeurs pertinentes attachées à ces entités ? Il s’agit ensuite d’identifier ce qui distingue le système du simple ensemble de ses entités constitutives : les interactions entre les entités. L’objectif de la modélisation peut aussi influer sur la façon d’aborder la mise en équation. S’agit-il de confirmer une hypothèse, de simuler des interactions, de prédire une grandeur, de contrôler un phénomène ?
Puis vient la phase de modélisation proprement dite, où ces interactions sont traduites en expressions mathématiques. Nombreux sont les cas, particulièrement en dehors de la physique, où les expressions mathématiques ne sont pas « données », mais résultent, elles aussi, d’une véritable construction et d’une suite d’énoncés d’hypothèses.
À toute étape du processus itératif de modélisation, les choix effectués lors des précédentes peuvent être remis en cause. Telle grandeur considérée comme non pertinente doit finalement être prise en compte ; telle formulation mathématique se révèle trop simpliste ou au contraire trop complexe, etc. Cette remise en cause peut résulter d’une expérimentation, soit numérique (le comportement n’est pas celui attendu, par exemple avec les équations proposées le ressort n’oscille pas), soit physique (les grandeurs calculées ne correspondent pas du tout à celles mesurées). De ce fait, le système et le modèle se co-construisent au cours de ce processus qui est itéré jusqu’à l’obtention des réponses aux questions qui ont motivé la démarche.
Enfin, ce n’est que dans des cas simples que le modèle obtenu sous la forme d’équations différentielles peut être résolu analytiquement, c’est-à-dire que l’expression mathématique des fonctions inconnues, telles que x(t), peut être obtenue. Le plus souvent, c’est uniquement par la résolution numérique qu’il est possible d’obtenir les valeurs des variables pour différentes valeurs de t.
Pour à la fois illustrer cette démarche constructiviste et faire comprendre la capacité de représentation et la lisibilité des équations différentielles, il faut chercher des exemples simples, mais « exemplaires ». Parce que les lois exprimées sous une forme mathématique y sont rares, voire inexistantes, les sciences de la vie, et plus spécifiquement la dynamique des populations, en offre d’excellents.
Un écosystème simple
Considérons ainsi un écosystème très simple, impliquant deux populations seulement : des proies (par exemple des lièvres) et leurs prédateurs (des lynx). Pour rester raisonnable, énonçons plusieurs hypothèses simplificatrices. De même que pour modéliser le système masselotte – ressort nous avons accepté les hypothèses que le ressort était parfait, que sa masse était faible par rapport à celle de la masselotte, que les différents ancrages étaient rigides, que le frottement était négligeable, et d’autres encore, nous considérons que les lièvres n’ont que les lynx pour prédateurs, que ceux-ci ne se nourrissent que de lièvres, et que les deux populations se partagent un même territoire qu’elles ne quittent pas.
Notons N l’effectif des lièvres et P l’effectif des lynx. La valeur de ces deux grandeurs évolue évidemment dans le temps : notons N(t) et P(t) les effectifs à l’instant t. Ce sont des grandeurs sans dimension.
Croissance exponentielle
Étudions d’abord la dynamique de la population des lièvres quand ils ne subissent pas la prédation des lynx. Nous faisons l’hypothèse supplémentaire qu’ils disposent de toutes les ressources nécessaires à leur développement : nourriture, espace, etc.
La population des lièvres augmente sous l’effet des naissances et décroît sous l’effet des décès. Entre deux instants t1 et t2 (t2 > t1), l’effectif N varie de la quantité N(t2) – N(t1). Cette valeur est positive s’il y a eu accroissement, et négative s’il y a eu diminution de l’effectif. Quoi qu’il en soit, cette variation est égale au solde des naissances et des décès dans l’intervalle de temps [t1, t2] :
N(t2) = N(t1) + ( Naiss [t1, t2] – Décès [t1, t2] ).
Le nombre de naissances Naiss [t1, t2] dans l’intervalle de temps [t1, t2] est égal à N(t1) multiplié par le taux de natalité supposé constant et par la durée (t2 – t1) de l’intervalle de temps [t1, t2] :
Naiss [t1, t2] = N(t1) . TauxNatalité . (t2 – t1).
Le taux de natalité est exprimé classiquement en nombre de naissances par individu et par unité de temps (par exemple par an, son unité est alors 1/an ou encore an-1). Plus généralement, sa dimension est l’inverse d’un temps ; sa multiplication par un intervalle de temps résulte en un nombre sans dimension, un effectif. Ainsi, si le taux de natalité vaut 0,03 an-1, une population de 1000 individus augmenterait en un an de 1000 × 0,03 × 1, soit 30 nouveaux individus.
Il en est de même pour les décès. En conséquence :
N(t2) = N(t1) + [ N(t1) . TauxNatalité . (t2 –t1)] – [N(t1) . TauxMortalité . (t2 – t1)] = N(t1) + N(t1) . (TauxNatalité – TauxMortalité) . (t2 – t1) = N(t1) + N(t1) . r . (t2 – t1)
où r, différence entre le taux de natalité et le taux de mortalité, est le taux de croissance, dit intrinsèque, de la population des lièvres.
Ce calcul de N au temps t2 applique le taux de natalité sur la valeur N(t1) comme si l’effectif de la population se maintenait à cette même valeur dans l’intervalle de temps [t1, t2].
Mais ce nombre de naissances est ici une approximation. En effet, rien dans nos hypothèses ne nous autorise à ne comptabiliser les naissances qu’au bout d’un an. On peut d’ailleurs calculer l’accroissement de la population sur 6 mois : 1000 × 0,03 × 0,5 = 15. De ce fait, au bout d’un an, l’accroissement de la population serait ainsi, calculé de 6 mois en 6 mois : 1000 × 0,03 × 0,5 + (1000 + 15) × 0,03 × 0,5 = 30,225.
Le fait de calculer des effectifs de populations à l’aide de nombres réels, et non pas avec des nombres entiers, peut être assez surprenant. C’est une conséquence directe du choix du formalisme des équations différentielles qui font intervenir des fonctions réelles et imposent une vision d’individus indéfiniment sécables…
Poursuivons. Si le calcul est fait de 3 mois en 3 mois, on trouve que l’accroissement sur un an est de 30,339 individus. Que se passe-t-il si nous réduisons encore et encore l’intervalle de calcul de l’accroissement ?
Écrivons :
N(t2) – N(t1) = r N(t1) (t2 – t1)
puis
[N(t2) – N(t1)] / (t2 – t1)= r N(t1)
Si la taille de l’intervalle [t1, t2] se réduit et tend vers 0, en faisant tendre t1 vers t2, le taux d’accroissement [N(t2) – N(t1)] / (t2 – t1) tend, par définition, vers la dérivée de la fonction N(t) au temps t2, c’est-à-dire dN(t2)/dt, ou encore N’(t2). De son côté, N(t1) tend évidemment vers N(t2). On obtient donc l’équation N’(t2) = r N(t2).
Plus généralement, à tout temps t, nous pouvons écrire l’équation différentielle : N’(t) = r . N(t), ou dN(t)/dt = r . N(t), ou encore dN(t) = r N(t) dt. Cette dernière notation exprime que, pendant un intervalle de temps dt très petit (« infinitésimal »), la population varie de la quantité r N(t) dt.
Cette équation différentielle, dont nous venons de suivre la genèse, est la plus simple que l’on puisse écrire pour un système dynamique. Elle exprime le fait qu’à tout instant, le taux d’accroissement de la quantité N(t) est proportionnel à la quantité elle-même. Si le coefficient de proportionnalité, ici r, est positif (ce qui traduit le fait que le taux de natalité est supérieur au taux de mortalité), on comprend que la quantité va s’accroître « de plus en plus vite ».
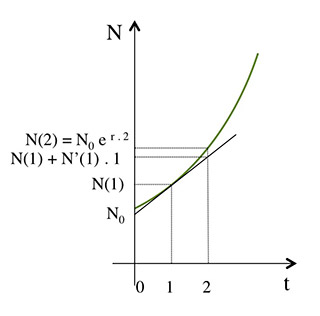
Si, à partir du temps t1 = 1, la croissance de N se poursuivait à une vitesse constante égale à la dérivée en ce point, c’est-à-dire avec la valeur N’(t1) = N’(1). N croîtrait linéairement pour atteindre, au temps t2 = 2, la valeur N(t1) + N’(t1). (t2-t1) = N(1) + N’(1) . 1 ≈ 1061,36. Mais la valeur de la dérivée N’(t) varie à chaque instant, puisqu’elle est égale à r . N(t). De fait, la valeur N(t2) = N(2) est égale à N0 e r .2 ≈ 1061,83.
Une équation différentielle est une équation fonctionnelle. Sa ou ses solutions ne sont pas des nombres, comme dans le cas des équations algébriques, mais des fonctions de la variable indépendante, ici le temps noté t.
L’équation N’(t)=r.N(t) ou encore dN(t)/dt = r . N(t) se résout facilement. Il suffit en effet de l’écrire sous la forme :
dN(t)/N(t) = r . dt
puis de chercher la primitive des deux membres, ce qui conserve l’égalité :
ln N = r . t + C où C est une constante arbitraire
En appliquant la fonction exponentielle aux deux membres de l’égalité, on obtient :
N = e rt+C=ert.eC= K ert
La constante K peut être déterminée par la connaissance d’un couple de valeurs (t, N(t)). Classiquement, le couple (0, N(0)) est utilisé :
N(0) = K e 0 = K
La fonction solution de l’équation différentielle est donc N(t) = N(0) e rt
Sa solution analytique est facile à obtenir : N(t) = N(0) e r t, où N(0) = N0, valeur de l’effectif des proies au temps t = 0, est la condition initiale du système dynamique.
Si la valeur de r est positive, l’effectif des proies croît de façon exponentielle.
Avec cette expression, il est possible de calculer N(1) quand N(0) vaut 1000 et r vaut 0,03 comme ci-dessus : N(1) = 1000 . e 0,03 . 1 ≈ 1030,45…, soit un accroissement d’environ 30,45 individus en un an.
À ce temps 1, la dérivée de N, dN/dt vaut 1030,45 × 0,03 ≈ 30,91… Cela signifie que, si cette vitesse de croissance, qui est donc exprimée en individus par an, se maintenait pendant un an, N(2) vaudrait 1030,45… + 30,91…, soit 1061,36…
Mais cette vitesse évolue et s’accroît proportionnellement à N, puisque sa valeur, selon l’équation différentielle, est à tout moment égale à r . N. De fait, on trouve que N(2) est égale à 1000 . e 0,03 . 2 ≈ 1061,83.
Un paramètre significatif de la croissance exponentielle est le temps de doublement de la grandeur impliquée. Soit τ ce temps ; il suffit d’écrire, par exemple, N(τ) = N(0) e r τ= 2 N(0) pour trouver τ = ln 2 / r, et vérifier que τ a bien pour dimension le temps. Le temps de doublement est utilisé dans la métaphore des nénuphars pour illustrer l’impact des décisions face à un processus de croissance exponentielle.
Un plant de nénuphar est placé dans un étang. La surface qu’il occupe double chaque jour, au détriment des autres plantes aquatiques. Dans les premiers temps, les propriétaires de l’étang ne se préoccupent pas de ce développement qui n’affecte encore qu’une faible partie de l’étang. Ce n’est qu’au moment où le nénuphar occupe la moitié de l’étang qu’ils décident de réagir. De combien de temps disposent-ils avant que le nénuphar recouvre tout l’étang ?
Cette métaphore est citée notamment par Albert Jacquard dans son livre L’Équation du nénuphar – Les plaisirs de la science (Livre de Poche).
C’est dès le lendemain que le nénuphar couvrira tout l’étang, puisqu’il double de surface chaque jour !
La croissance du plant de nénuphar suit une loi géométrique de raison 2 : si Sj est la surface qu’il occupe au jour j, alors Sj+1 = 2 Sj, ou encore Sj = 1/2 Sj+1. Si donc au 25e jour, ou plus généralement au jour j, il occupe la moitié de la surface du bassin, il en occupera l’intégralité le jour suivant j+1.
Visualiser la croissance exponentielle sur une animation
Cette animation vous permet de visualiser la croissance exponentielle.
Après avoir choisi les valeurs de la condition initiale N0, ainsi que du taux de croissance r (dont est déduit le temps de doublement, noté τ ; τ = ln 2 / r), vous observez la courbe de la croissance de N. L’instant τ où la population initiale double est indiqué sur l’axe des temps, en abscisse. Les valeurs 2N0, 4N0, etc. figurent en ordonnée.
Vous pouvez afficher jusqu’à 5 courbes simultanément pour les comparer.
Attention, écrivez les nombres décimaux avec un point et non une virgule.
Visualiser la décroissance exponentielle sur une animation
La même analyse peut être conduite pour la population des lynx. En l’absence des proies dont ils se nourrissent exclusivement, leur effectif P(t) satisfait l’équation différentielle P’ = – m P, avec m positif. Le coefficient – m traduit ici le fait que, en l’absence de proies et donc de nourriture, le taux de mortalité est supérieur au taux de natalité.
La solution analytique de l’équation est semblable à la précédente : P(t) = P(0) e – m t ; P décroît de façon exponentielle. Le paramètre λ = 1/m a pour dimension le temps.
Cette animation vous permet de visualiser la décroissance exponentielle.
Après avoir choisi les valeurs de la condition initiale P0, ainsi que du taux de mortalité m (dont est déduit le temps de demi-vie, ici noté τ ; τ = ln 2 / m), vous observez la courbe de la décroissance de P. L’instant τ où la population initiale est divisée par 2 est indiqué sur l’axe des temps, en abscisse. La valeur P0/2 correspondante figure en ordonnée.
Vous pouvez afficher jusqu’à 5 courbes simultanément pour les comparer.
Attention, écrivez les nombres décimaux avec un point et non une virgule.
Soit l’équation différentielle dx(t)/dt = – x / λ avec λ > 0 ; la valeur de x décroit exponentiellement à partir de sa valeur initiale x(0).
Si la population x décroît dans le temps c’est que les individus qui la composent la quittent, quelle qu’en soit la cause. Certains la quittent très tôt, peu après le temps t = 0, d’autres plus tard, certains jamais puisque la courbe tend asymptotiquement vers 0.
C’est à l’aide d’un peu de mathématiques qu’il est possible de démontrer que λ est la durée de résidence moyenne d’un individu dans la population d’effectif initial x0.
Considérons un exemple simple pour comprendre la formalisation mathématique utilisée plus bas. Imaginons que 10 lettres soient postées un même jour pour une même destination. On constate que 2 lettres arrivent le lendemain, 5 le surlendemain et 3 le jour d’après encore. Quel est le temps moyen de résidence d’une lettre dans le circuit postal ? La réponse est (2 × 1 + 5 × 2 + 3 × 3) / 10, soit 2,1 jours. Cet exemple est « discret » au sens où il fait intervenir des entités distinctes et des nombres entiers. Il nous faut trouver son équivalent continu, faisant intervenir des nombres réels.
Entre deux instants très proches t et t + dt, le nombre dx(t) d’individus qui quittent la population est (- x(t) / λ) dt, soit –( x0e t /λ)/λ dt ; ils y seront restés pendant l’intervalle [0, t].
Pour obtenir le temps moyen de résidence dans la population, par analogie avec l’exemple des lettres, il faut faire la somme de tous les temps de résidence et diviser l’ensemble par l’effectif initial x(0). Le temps de résidence moyen est donc égal à :
\[\frac{1}{x_0} \int_{0}^{\infty} t \frac{{x_0}{e}^{-\frac{t}{\lambda}}}{\lambda} dt
= \frac{1}{\lambda} \int_{0}^{\infty} t {e}^{-\frac{t}{\lambda}} dt\]
En intégrant par parties, on trouve que l’intégrale a pour valeur λ2, et que le temps de résidence moyen vaut donc bien λ.
Croissance logistique
« Celui qui croit qu’une croissance exponentielle peut continuer indéfiniment
dans un monde fini est soit un fou, soit un économiste. »
Kenneth E. Boulding
Reconsidérons à présent la croissance exponentielle. À l’évidence, il n’est pas réaliste d’imaginer qu’une population animale puisse croître exponentiellement sans rencontrer à un moment ou à un autre des limites à sa croissance. En effet, elle exploite des ressources qui sont évidemment limitées ; ainsi en va-t-il de l’herbe pour nos lièvres, ou plus simplement encore de la superficie du territoire disponible. Pour tenir compte de ces limites, il convient de modifier l’équation différentielle qui rend compte de la croissance de l’effectif N. Nous introduisons ainsi un terme de freinage dans l’équation de croissance de la population des proies non soumises à prédation. La nouvelle équation s’écrit alors :
\[\frac{dN}{dt} = r(1-\frac{N}{K}) N \]
où K est un paramètre à valeur positive, appelé « capacité limite ».
Après une phase exponentielle, durant laquelle la valeur de N est encore petite devant celle de K, la courbe de croissance s’infléchit et tend asymptotiquement vers K. En effet, considérons une valeur initiale de N, N0 = N(0) positive et inférieure à K : 0 < N0 < K ; la dérivée en t = 0, r N0 (1 – N0 / K) est positive et donc N croît ; la valeur du terme N/K croît également et tend vers 1 ; (1 – N / K) tend donc vers 0 et entraîne N’ avec elle. N’ reste cependant positive, N continue donc à croître, mais toujours plus lentement en approchant de la valeur K. Cette courbe d’évolution « en S » est caractéristique de cette croissance dite « logistique ».
Visualiser la croissance logistique sur une animation
Cette animation vous permet de visualiser la croissance logistique.
Outre la valeur du paramètre r (taux de croissance intrinsèque), vous pouvez modifier la valeur du paramètre K, la capacité limite. Après avoir lancé la simulation avec la valeur de K suggérée, ou une valeur proche de celle-ci, lancez la simulation avec une valeur de K beaucoup plus importante. Vous ne verrez alors sur le graphique que la phase de croissance exponentielle. Vous constaterez que les courbes se superposent à leur début avant de diverger plus ou moins rapidement suivant la valeur de K.
Vous pouvez afficher jusqu’à 5 courbes simultanément pour les comparer.
Attention, écrivez les nombres décimaux avec un point et non une virgule.
L’équation différentielle est non-linéaire. Elle peut en effet se réécrire sous la forme suivante :
\[\frac{dN}{dt} = r N – r\frac{N^2}{K}\]
Elle possède la solution explicite :
\[N(t) = \frac{{N_0} {e}^{rt}}{1 +{\dfrac {{N_0} ({e}^{rt} -1)}{K}}}\]
Quel est l’intérêt de cette formulation ? C’est en fait la plus simple qui permette de rendre compte d’une croissance en milieu limité. Plusieurs autres formulations possibles ont d’ailleurs été proposées dans l’abondante littérature scientifique portant sur les modèles de croissance en dynamique des populations.
La modélisation, une démarche à poursuivre
Par ailleurs, les populations ne restent pas isolées. Proies et prédateurs interagissent… Ils se rencontrent. Le nombre de proies et le nombre de prédateurs dépendent l’un de l’autre, et là encore, des équations différentielles en rendent compte. Les modèles proie-prédateur permettent d’étudier la dynamique de ces populations.
Réalisation des animations : Ouest INSA, sur la base d’applets réalisées par Hamdi Ben Abdallah, avec des compléments proposés par Jocelyne Erhel.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !
