
Un algorithme pour mettre en rang une équipe de football
1. Aligner des joueurs sur un terrain
Lors de la coupe du monde de football 2010, l’équipe d’Allemagne a chuté en demi-finale mais a impressionné par sa qualité de jeu et par sa rigueur. Le sélectionneur avait mis au point une méthode infaillible pour aligner les joueurs avant d’écouter l’hymne national. Comme il n’a pas utilisé cet algorithme pour les matches, on n’a pas pu en admirer l’efficacité : merci au professeur Ulrich Rüde et à Christoph Freundl, de l’Université d’Erlangen, de nous l’avoir communiqué.
Tous les joueurs sont sur le terrain, en train de s’échauffer, et peuvent se déplacer sur toute la surface. Puis ils doivent former une ligne droite, matérialisée par des drapeaux aux extrémités. Ces drapeaux sont bien sûr retirés avant de jouer et l’alignement ne sert pas pendant la phase de jeu.
Les joueurs doivent se placer entre les deux drapeaux, pour former une ligne, et se positionner à intervalles réguliers. Ils portent un maillot avec un numéro de 1 à 11. Le joueur 1 doit se trouver près du drapeau de gauche, puis le joueur 2 à côté, et ainsi de suite, jusqu’au joueur 11, avant le drapeau de droite.
La méthode allemande
Au départ, les joueurs sont éparpillés sur le terrain. Intuitivement, la ligne sera réalisée si chaque joueur portant le maillot i est au milieu des joueurs voisins, avec les maillots (i-1) et (i+1), pour i variant de 2 à 10. Par exemple, le joueur 4 est au milieu des joueurs 3 et 5. Le joueur 1 est entre le drapeau de gauche et le joueur 2 ; le joueur 11 est entre le joueur 10 et le drapeau de droite.
Le sélectionneur agit du bord du terrain. Il appelle, avec son sifflet, les joueurs l’un après l’autre et leur dit de se placer au milieu des joueurs voisins : le joueur avec le maillot 1 se place au milieu du drapeau de gauche et du joueur 2, puis le joueur 2 se place au milieu des joueurs 1 et 3 ; ainsi de suite, jusqu’au joueur 11 qui se place au milieu du joueur 10 et du drapeau de droite. Les joueurs ne sont pas encore alignés, loin de là. Alors le sélectionneur recommence les déplacements. Il utilise ainsi un algorithme itératif. Chaque itération consiste à placer les 11 joueurs l’un après l’autre et nécessite ainsi 11 déplacements de joueurs.
Au bout de plusieurs itérations, les joueurs forment plus ou moins un rang. S’ils pouvaient continuer à se déplacer indéfiniment, ils finiraient par être tout à fait alignés. L’algorithme converge vers le résultat voulu, qui est une ligne droite. La convergence est garantie, quelle que soit la position de départ des joueurs. Le sélectionneur arrête de déplacer ses joueurs quand il considère que l’alignement est assez bon. Il utilise un critère d’arrêt de l’algorithme itératif.
Chaque itération prend un peu de temps, car chaque joueur i attend que le joueur (i-1) ait bougé pour se déplacer à son tour. C’est pourquoi le sélectionneur a imaginé une autre version. Il déplace d’abord les joueurs avec un numéro pair, puis les joueurs avec un numéro impair. Du coup, tous les joueurs pairs peuvent se déplacer ensemble, puisqu’ils se placent au milieu de joueurs impairs qui bougeront après eux. Ainsi, le joueur 2 se positionne entre le joueur 1 et le joueur 3, en même temps que le joueur 4 entre le joueur 3 et le joueur 5, etc. Puis tous les joueurs impairs peuvent se déplacer ensemble, puisqu’ils se placent au milieu de joueurs pairs qui ont fini de bouger. Les itérations peuvent également continuer jusqu’à former une ligne presque droite. On observe qu’il faut un peu plus d’itérations. Par contre, chaque itération prend moins de temps, parce que les joueurs peuvent se déplacer simultanément. Il y a ainsi un compromis à trouver entre la vitesse d’exécution de chaque itération et la vitesse de convergence de l’algorithme.
Pour accéder à l’applet Java, autorisez les applets du domaine https://interstices.info. Si votre navigateur n’accepte plus le plug-in Java, mais que Java est installé sur votre ordinateur, vous pouvez télécharger le fichier JNLP, enregistrez-le avant de l’ouvrir avec Java Web Start.
Applet réalisée par Régis Monte, d’après Christoph Freundl.
Tout le monde sait que l’équipe de France n’a pas brillé à la coupe du monde 2010. Le nouveau sélectionneur décide de prendre les choses en main et de tester l’algorithme des Allemands. Pour un stage d’entraînement, il a sélectionné 31 joueurs avec les maillots numérotés de 1 à 31. La règle du jeu est la même, il faut former une ligne entre deux drapeaux, avec les joueurs espacés régulièrement. Les joueurs sont placés au hasard sur le terrain puis, au coup de sifflet, chacun doit se placer au milieu de ses voisins. Le sélectionneur choisit d’appeler les joueurs un par un, dans l’ordre de 1 à 31. On observe qu’il faut beaucoup d’itérations pour obtenir un alignement acceptable. L’algorithme converge toujours, mais beaucoup plus lentement. Pourtant, les Français ont obéi au sélectionneur. Mais ils sont plus nombreux que les Allemands. La vitesse de convergence de l’algorithme dépend du nombre de joueurs : plus les joueurs sont nombreux, plus il faut d’itérations.
La méthode espagnole
L’équipe d’Espagne est championne du monde en 2010. Est-ce parce que leur sélectionneur a adopté une méthode différente ?
Pour simplifier, on va supposer que les drapeaux sont sur la ligne de touche, qui est donc tracée. Le sélectionneur utilise des outils : avec un mètre, il mesure la longueur L de cette ligne, puis, avec une calculatrice, il calcule la distance d entre deux joueurs. Lorsqu’il y a 11 joueurs, on a d = L/12; lorsqu’il y a 31 joueurs, on a d = L/32. Ensuite, le sélectionneur prend un bâton, fait une marque sur le bâton à la distance d.
Au coup de sifflet, le joueur 1 prend le bâton, va se placer sur la ligne, près du drapeau de gauche; il mesure sa place grâce au bâton, il est ainsi à la distance d du drapeau. Au coup de sifflet suivant, le joueur 2 prend le bâton et va se placer sur la ligne, près du joueur 1, à une distance d. Ainsi de suite, jusqu’au joueur 11. Ainsi, tous les joueurs sont sur la ligne, matérialisée sur le terrain, et sont espacés régulièrement avec une distance d entre les joueurs. Si les mesures sont justes et si les joueurs ont bien utilisé le bâton, le joueur 11 est à une distance d du drapeau de droite.
Le sélectionneur espagnol a utilisé un algorithme direct : il n’y a pas d’itérations. Grâce au bâton étalonné, chaque joueur ne se déplace qu’une seule fois, soit au total 11 déplacements, pour obtenir un alignement parfait. Avec 31 joueurs, il y a au total 31 déplacements.
La méthode du XV de France
Le XV de France rend visite à l’équipe de foot. Les joueurs de rugby font le pari qu’ils peuvent s’aligner entre les drapeaux, sans faire de mesure, avec 15 déplacements de joueurs, mais en seulement 4 étapes. Pari tenu, les joueurs de rugby font la démonstration.
Le joueur 8 se place au milieu des drapeaux. Ensuite, le joueur 4 va se placer au milieu du drapeau de gauche et du joueur 8, tandis que le joueur 12 va se placer en même temps au milieu du joueur 8 et du drapeau de droite. Troisième étape, les joueurs 2, 6, 10 vont se positionner à leur place, en même temps, au milieu des joueurs déjà placés (par exemple, le 6 au milieu du 4 et du 8). Quatrième et dernière étape, les joueurs impairs vont se placer au milieu des joueurs pairs, tous en même temps.
Pour accéder à l’applet Java, autorisez les applets du domaine https://interstices.info. Si votre navigateur n’accepte plus le plug-in Java, mais que Java est installé sur votre ordinateur, vous pouvez télécharger le fichier JNLP, enregistrez-le avant de l’ouvrir avec Java Web Start.
Applet réalisée par Régis Monte.
Le XV de France a donc gagné son pari. L’équipe de rugby a utilisé un algorithme direct parallèle. Comme avec l’algorithme espagnol, il y a 15 déplacements, mais ces déplacements peuvent se faire simultanément, ce qui permet d’aligner parfaitement les joueurs en 4 étapes.
Le sélectionneur de foot veut essayer l’algorithme, encore mieux, avec 31 joueurs. En 5 coups de sifflet, le tour est joué :
- 1er coup de sifflet : joueur 16 au milieu des drapeaux.
- 2e coup de sifflet : joueurs 8 et 24 à leur place.
- 3e coup de sifflet : joueurs 4, 12, 20, 28 en poste.
- 4e coup de sifflet : joueurs 2, 6, 10, 14, 18, 22, 26, 30 sur la ligne.
- 5e coup de sifflet : joueurs impairs pour finir.
Le capitaine de rugby lance alors un nouveau défi : utiliser l’algorithme avec seulement une équipe de 11 joueurs. C’est parti :
- 1er coup de sifflet : joueur 6 au milieu.
- 2e coup de sifflet : joueurs 3 et 9 de chaque côté du joueur 6.
- 3e coup de sifflet : cela coince ! il faut utiliser un algorithme permettant de placer 2 joueurs entre 2 autres. Admettons que 2 joueurs sachent faire cela, avec un algorithme direct comme celui des Espagnols. Alors, les joueurs 1 et 2 vont se placer entre le drapeau et le joueur 3. En même temps, les joueurs 4 et 5 se positionnent, ainsi que les joueurs 7 et 8, et les joueurs 10 et 11.
Au prix d’une petite modification de l’algorithme, il fonctionne ainsi avec un nombre quelconque de joueurs. Il faut savoir placer un joueur au milieu de deux autres et aussi placer deux joueurs ensemble, chacun à une distance d/2 du milieu (d étant la distance entre deux joueurs). Ainsi, l’équipe de France de foot va se déplacer très rapidement sur le terrain et — qui sait ? — réaliser des prouesses.
2. Du sport de ballon au sport cérébral
Mais ne nous égarons pas et revenons aux algorithmes.
Les joueurs de foot mis en équations
Essayons de modéliser l’exercice précédent, avec un peu de formules mathématiques et quelques notations. L’équipe contient n joueurs. Les positions des joueurs sont repérées par leurs coordonnées (xi,yi), i = 1, 2… n. xi est la position horizontale du joueur i et yi sa position verticale. Les positions des drapeaux sont connues et sont aussi repérées par leurs coordonnées : (x0, y0) et (xn+1, yn+1). Mettre les joueurs au milieu de leurs voisins se traduit par les équations suivantes :
xi = (xi-1 + xi+1)/2,
yi = (yi-1 + yi+1)/2,
avec i qui varie de 1 à n. On a donc deux systèmes de n équations à n inconnues, dont les équations sont presque les mêmes. Ces deux systèmes ont une solution unique : il n’y a qu’une façon d’aligner les joueurs.
Pour simplifier, nous étudions maintenant seulement les positions horizontales. On a donc 2 données connues x0 et xn+1 et n inconnues x1, x2… xn, avec les n équations :
x1 = (x0 + x2)/2,
x2 = (x1 + x3)/2,
…,
xn = (xn-1 + xn+1)/2.
Si on connaissait x2, on pourrait calculer x1. Si on connaissait x1 et x3, on pourrait calculer x2. Il faut réussir à calculer ensemble x1, x2… xn, c’est-à-dire résoudre le système d’équations.
Il s’agit d’un système linéaire : chaque équation traduit des proportions entre les inconnues et les données. Ici, une inconnue est au milieu des deux autres. Par comparaison, l’équation x2 = (x12 + x32)/2 par exemple, n’est pas linéaire : x2 n’est pas proportionnel à x1 et x3.
Ce système linéaire est particulier, car chaque équation ne fait jouer que trois inconnues consécutives : l’équation i traduit une proportion (le milieu) entre les positions xi, xi-1, xi+1. On appelle ce système un système tridiagonal.
Le mot tridiagonal provient du mode de rangement des nombres manipulés : les inconnues sont rangées dans un vecteur, les données sont dans autre vecteur, tandis que les coefficients de proportionnalité sont dans une matrice avec n lignes et n colonnes. On écrit ensuite le système linéaire en utilisant les règles des opérations sur les matrices et les vecteurs. Pour un système tridiagonal, les termes non nuls sont ainsi rangés le long de trois diagonales. Par exemple, avec n = 6, on écrit le système de la façon suivante :
 |
1 | -1/2 | 0 | 0 | 0 | 0 |  |
 |
x1 |  |
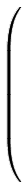 |
x0/2 | 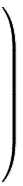 |
|
| -1/2 | 1 | -1/2 | 0 | 0 | 0 | x2 | 0 | |||||||
| 0 | -1/2 | 1 | -1/2 | 0 | 0 | x3 | 0 | |||||||
| 0 | 0 | -1/2 | 1 | -1/2 | 0 | x4 | = | 0 | ||||||
| 0 | 0 | 0 | -1/2 | 1 | -1/2 | x5 | 0 | |||||||
| 0 | 0 | 0 | 0 | -1/2 | 1 | x6 | x7/2 |
Le mot bidiagonal provient également du mode de rangement des nombres manipulés. Pour un système bidiagonal, les termes non nuls sont ainsi rangés le long de deux diagonales. Par exemple, avec n = 6, on écrit le système espagnol de la façon suivante :
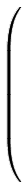 |
1 | 0 | 0 | 0 | 0 | 0 | 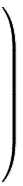 |
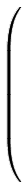 |
x1 | 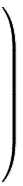 |
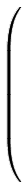 |
x0+ d | 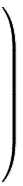 |
|
| -1 | 1 | 0 | 0 | 0 | 0 | x2 | d | |||||||
| 0 | -1 | 1 | 0 | 0 | 0 | x3 | d | |||||||
| 0 | 0 | -1 | 1 | 0 | 0 | x4 | = | d | ||||||
| 0 | 0 | 0 | -1 | 1 | 0 | x5 | d | |||||||
| 0 | 0 | 0 | 0 | -1 | 1 | x6 | d |
Comment résoudre un système tridiagonal ?
Premier point important : le problème des joueurs considéré ici a une solution et une seule. Certains systèmes ont aussi une solution unique. Par contre, il existe des systèmes qui n’ont pas de solution, d’autres qui ont une infinité de solutions.
Nous avons vu trois algorithmes :
- l’algorithme des Allemands. Cette technique itérative s’appelle l’algorithme de Gauss-Seidel, du nom de ses inventeurs. Il a d’abord été inventé en 1823 par Carl Friedrich Gauss, un très grand mathématicien allemand. Il a ensuite été développé par un de ses collègues, Ludwig Seidel. L’algorithme fonctionne pour tout système tridiagonal. Le nombre d’opérations (les déplacements des joueurs) à chaque itération est proportionnel à n. La solution trouvée est une approximation. L’algorithme converge vers la solution exacte et le nombre d’itérations varie avec n, sous certaines hypothèses sur le système tridiagonal. La version pair-impair permet de déplacer des joueurs en parallèle, par contre, elle augmente le nombre d’itérations. Nous allons y revenir plus loin.
- l’algorithme des Espagnols. La technique présentée ici est spécifique du système tridiagonal considéré. Elle ne peut pas se généraliser à un système tridiagonal quelconque. Mais on peut définir un algorithme direct pour tout système tridiagonal et pour tout système linéaire. L’algorithme direct le plus utilisé s’appelle l’algorithme de Gauss, du nom du même mathématicien allemand. Avec cet algorithme direct, il n’y a pas d’itération et la solution trouvée est exacte (aux erreurs d’arrondi près). Pour un système tridiagonal, le nombre d’opérations est proportionnel à n ; si on multiplie le nombre d’inconnues par 10, on multiplie aussi le nombre d’opérations par 10 : la complexité est linéaire. L’algorithme est séquentiel : les joueurs se placent l’un après l’autre.
- l’algorithme des rugbymen. C’est un algorithme direct, avec une complexité linéaire, comme l’algorithme des Espagnols ; la solution est exacte et le nombre d’opérations est proportionnel à n. Mais il est aussi parallèle. Il positionne (2p – 1) joueurs en p étapes (p = 4 pour n = 15 et p = 5 pour n = 31).
Les deux algorithmes directs vont très vite. Pourquoi alors utiliser l’algorithme de Gauss-Seidel ?
La version parallèle (l’algorithme des rugbymen) ne fonctionne que pour les systèmes tridiagonaux. Il existe plusieurs variantes parallèles, assez similaires (réduction cyclique, etc). Mais il est difficile de généraliser cet algorithme à un système non tridiagonal.
L’algorithme direct de Gauss fonctionne pour tout système qui possède une solution unique, à condition de permuter parfois les équations (stratégie du pivot de Gauss). Mais le nombre d’opérations pour un système général (non tridiagonal) n’est plus proportionnel à n. Dans le cas d’un système général, chaque équation fait intervenir toutes les inconnues et on montre que le nombre d’opérations de l’algorithme direct de Gauss est proportionnel à n3 ; donc, si on multiplie par 10 le nombre d’inconnues, on multiplie par 1000 le nombre d’opérations : la complexité est cubique.
L’algorithme de Gauss-Seidel fonctionne aussi pour tout système qui possède une solution unique, à condition qu’on ne fasse pas de division par 0 (ce qui est bien sûr interdit). Par contre, il ne converge pas à tous les coups et il converge plus ou moins vite. Dans le cas général, le nombre d’opérations à chaque itération est proportionnel à n2. Au total, avec m itérations, l’algorithme nécessite donc un nombre d’opérations proportionnel à n2m. Donc si m < n, l’algorithme de Gauss-Seidel nécessite moins d’opérations que celui de Gauss (on considère un nombre égal à n3 et à n2m, en négligeant les constantes de proportionnalité).
3. L’algorithme de Gauss et ses variantes
L’algorithme des Espagnols
L’algorithme des Espagnols utilise une transformation du problème, qui est ici basée sur un argument géométrique : on sait que tous les joueurs sont équidistants, et que la distance entre deux joueurs vaut d = L/(n+1). On obtient le système d’équations suivant, qui est équivalent au système tridiagonal de départ :
x1 = x0 + d,
x2 = x1 + d,
…,
xn = xn-1 + d.
Ce système est très particulier, car on peut le résoudre pas à pas. En effet, avec la première équation, on calcule x1; ensuite, avec la deuxième équation, puisqu’on connaît x1, on peut calculer x2; et ainsi de suite. Le système est bidiagonal.
L’algorithme utilise un principe de base : par une transformation, on aboutit à un problème équivalent, plus simple, que l’on sait résoudre. C’est le principe appliqué dans l’algorithme de Gauss. La transformation utilise ici un argument géométrique, alors que l’algorithme de Gauss utilise des calculs algébriques, mais le résultat est aussi un système bidiagonal.
L’algorithme des rugbymen
L’algorithme des rugbymen utilise une autre transformation du problème, elle aussi basée sur un argument géométrique : lorsque n = 2p – 1, le joueur m = (n+1)/2 est exactement au milieu des drapeaux. On calcule donc xm = (x0 + xn+1)/2, on sépare l’équipe des joueurs en deux et on obtient les deux systèmes suivants :
| x1 = (x0 + x2)/2, x2 = (x1 + x3)/2, …, xm-1 = (xm-2 + xm)/2. |
xm+1 = (xm + xm+2)/2, …, …, xn = (xn-1 + xn+1)/2. |
On a ainsi deux systèmes indépendants à résoudre, qui sont des systèmes tridiagonaux avec m-1 équations et m-1 inconnues. Pour obtenir l’équation avec xm dans le cas général, il faut utiliser la transformation algébrique de l’algorithme de Gauss.
L’algorithme utilise un autre principe de base : la récursivité. Il suffit d’appliquer le même procédé aux systèmes tridiagonaux et le tour est joué. En effet, m-1 = (n+1)/2 -1 = 2p-1 -1, donc on peut appliquer la récursion en remplaçant n par m-1. On aboutit finalement à un système d’une équation à une inconnue que l’on sait résoudre. En déroulant la récursion, on obtient bien l’algorithme des rugbymen : on place d’abord le joueur du milieu, puis les deux joueurs du milieu de chaque côté, puis les quatre joueurs du milieu dans les quatre intervalles, etc.
De plus, l’algorithme est parallèle ; il utilise encore un principe de base : diviser pour régner. Les deux systèmes indépendants peuvent être résolus en parallèle. En déroulant la récursion, on place un joueur, puis deux en même temps, puis quatre en même temps, etc.
4. L’algorithme de Gauss-Seidel
L’algorithme de Gauss-Seidel utilise des approximations et procède par itérations. Bien qu’il fonctionne pour tout système général, nous le présenterons ici pour le système tridiagonal des joueurs. Au début, les joueurs ne sont pas en ligne, aux positions x1(0), x2(0)… xn(0). À la première itération, le joueur 1 se place entre le drapeau de gauche et le joueur 2, puis le joueur 2 se place entre le joueur 1 et le joueur 3. Les nouvelles positions sont notées x1(1); x2(1)… xn(1) et sont calculées par les formules :
x1(1) = (x0 + x2(0))/2,
x2(1) = (x1(1) + x3(0))/2,
…
xi(1) = (xi-1(1) + xi+1(0))/2,
…
xn(1) = (xn-1(1) + xn+1)/2.
Rappelons que x0 et xn+1 sont connus, puisque ce sont les coordonnées des drapeaux. À présent, on n’a plus d’équation à résoudre, mais une formule à calculer : on connaît xi-1(1) et xi+1(0), donc on peut calculer xi(1). On peut entrer cette formule dans l’ordinateur qui va faire les opérations.
À la deuxième itération, on calcule :
x1(2) = (x0 + x2(1))/2,
x2(2) = (x1(2) + x3(1))/2,
…
xi(2) = (xi-1(2) + xi+1(1))/2,
…
xn(2) = (xn-1(2) + xn+1)/2.
Et ainsi de suite. À l’itération k, on calcule :
x1(k) = (x0 + x2(k-1))/2,
x2(k) = (x1(k) + x3(k-1))/2,
…
xi(k) = (xi-1(k) + xi+1(k-1))/2,
…
xn(k) = (xn-1(k) + xn+1)/2.
On poursuit ce processus itératif jusqu’à obtenir un alignement correct.
Convergence de l’algorithme de Gauss-Seidel
Pour étudier la convergence de l’algorithme, on introduit l’erreur commise par l’approximation. Il faut encore quelques notations. Soit a1, a2… an l’unique solution du système (les positions des joueurs sur la ligne). On définit les erreurs ei(k) à l’itération k par ei(k) = xi(k)-ai. Pour n’avoir qu’un seul nombre à manipuler, on définit l’erreur globale par e(k)2 = e1(k)2 +e2(k)2 +…+ ei(k)2 +…+ en(k)2. On utilise des carrés pour être sûr qu’on n’ajoute que des nombres positifs. On démontre qu’il existe un nombre r, qui dépend du système et de sa taille, tel que e(k + 1) ≤ re(k).
Autrement dit, à chaque itération, l’erreur est multipliée par r. De proche en proche (par récurrence), on obtient donc e(k) ≤ rke(0). Autrement dit, l’erreur à l’itération k est plus petite que l’erreur du début multipliée par le nombre r élevé à la puissance k.
Si r < 1 alors rk devient de plus en plus petit quand k augmente et converge vers 0. Donc, une condition suffisante pour que l’algorithme de Gauss-Seidel converge est que r soit strictement plus petit que 1. L’algorithme converge alors quel que soit le point de départ. Dans ce cas, on voit que l’erreur à l’itération k + 1 est plus petite que l’erreur à l’itération k : la convergence est monotone. Si on revient à l’exemple des joueurs de foot, on peut démontrer que r < 1. Donc l’algorithme converge, quelle que soit la position de départ des joueurs ; les joueurs se rapprochent de la ligne à chaque itération.
Grâce à cette convergence monotone, on peut définir un critère d’arrêt. En effet, l’idéal serait de dire qu’on s’arrête lorsque l’erreur est assez petite. Mais si on savait calculer l’erreur, alors on saurait calculer la solution. Si le problème était résolu, pourquoi essayer de le résoudre ?!
Donc, définissons un critère d’arrêt avec les approximations calculées. En fait, on va définir l’écart entre deux approximations successives par di(k) = xi(k)-xi(k-1) et globalement par d(k)2 = d1(k)2 + d2(k)2 +…+ di(k)2 +…+ dn(k)2. On montre qu’on a aussi d(k + 1) ≤ rd(k).
Le critère d’arrêt est alors simple : on arrête lorsque d(k) est assez petit. En effet, on sait que si on continue, les écarts entre les approximations vont être de plus en plus petits. Ce critère est ici justifié. Mais pour d’autres algorithmes itératifs, on n’a pas cette convergence monotone. On ne sait donc pas si, par hasard, l’écart est devenu petit mais va augmenter à nouveau. Il est alors plus difficile de définir un critère d’arrêt.
On a ainsi déterminé une condition suffisante de convergence. Si r > 1, on ne sait pas conclure sur la convergence. La condition r < 1 n’est pas nécessaire. Mais on peut trouver des systèmes avec r > 1 pour lesquels l’algorithme ne converge pas.
Lorsque r est très petit, rk converge très vite vers 0, donc l’erreur e(k) aussi. Mais lorsque r est proche de 1, rk converge très lentement et on observe souvent que l’algorithme de Gauss-Seidel converge aussi lentement. Pour le système tridiagonal des joueurs de foot, le nombre r augmente avec le nombre de joueurs. C’est pour cela qu’il faut plus d’itérations avec 31 joueurs qu’avec 11 joueurs.
De l’algorithme de Gauss-Seidel à l’algorithme multigrille
En pratique, on observe donc que le nombre d’itérations augmente rapidement avec le nombre n d’inconnues. De nos jours, ce sont des systèmes d’équations avec des millions d’inconnues qui doivent être résolus. Malgré l’accroissement de la puissance de calcul des ordinateurs, l’algorithme de Gauss-Seidel prendrait trop de temps, c’est pourquoi il n’est plus utilisé tel quel.
Il sert d’ingrédient de base dans la composition d’un autre algorithme, qu’on appelle multigrille. Le principe qui gouverne l’algorithme multigrille consiste à définir plusieurs niveaux imbriqués, de l’ordre de quelques dizaines, en associant à chaque niveau un système linéaire. Les niveaux étant classés du plus grand système au plus petit, on considère tout d’abord le niveau le plus élevé et celui immédiatement inférieur, et le petit système sert à corriger l’erreur commise dans le grand système. On descend ensuite d’un niveau, et ainsi de suite, jusqu’à arriver au niveau le plus bas. On remonte alors en sens inverse, puis on enchaîne les cycles, jusqu’à ce que l’algorithme converge. Les mathématiciens démontrent, toujours sous certaines hypothèses et pour certains systèmes, que l’algorithme multigrille converge très vite. De plus, le nombre d’itérations ne dépend alors pratiquement pas du nombre d’inconnues.
L’idée d’illustrer l’algorithme de Gauss-Seidel par une équipe de football vient de Ulrich Rüde et Christoph Freundl, dans leur article Gauß-Seidel Iteration zur Berechnung physikalischer Probleme paru en allemand dans la série Algorithmus der Woche publiée à l’occasion de l’Année de l’informatique (Informatikjahr) 2006.
L’adaptation et la programmation des applets en français a été réalisée par Régis Monte.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Jocelyne Erhel
Directrice de recherche émérite Inria, chercheuse en modélisation et simulation pour les sciences de l'environnement.