Vers une cryptographie en boîte blanche ?

Le mot « cryptographie » est dérivé de « kryptos » qui signifie « caché » ou « secret » en grec ancien et de « graphein » qui signifie « écrire ». L’objectif premier de la cryptographie est donc de protéger la confidentialité des messages écrits. Si elle a été inventée à l’origine pour des besoins militaires, la cryptographie est désormais partout. Les banques, les hôpitaux et de nombreuses entreprises l’utilisent pour protéger leurs données confidentielles. Elle est présente dans notre vie de tous les jours même si nous n’en avons pas toujours conscience, lorsque nous faisons un paiement par carte bancaire par exemple.

Le processus visant à transformer un message lisible en une suite de caractères a priori incompréhensible est appelé « chiffrement » et la transformation inverse est appelée « déchiffrement ». Bien sûr, le déchiffrement ne doit être possible que pour le destinataire du message : il nécessite la connaissance d’une clé cryptographique, un secret connu uniquement du destinataire et éventuellement de l’expéditeur du message. Sans la connaissance de la clé, le déchiffrement doit être un problème algorithmiquement difficile. L’existence de tels problèmes repose sur des hypothèses de complexité algorithmique non démontrées, mais que des années de recherche intensive n’ont pas suffi à invalider, tels que la difficulté de factoriser de grands nombres ou de calculer le logarithme discret, qui semblent donc suffisamment difficiles pour être utilisés.

Figure 1. Cryptographie symétrique (par opposition à la cryptographie asymétrique) : la clé utilisée par les deux parties est identique.

L’objectif d’un attaquant varie en fonction du contexte : récupérer la clé, parvenir à déchiffrer un message ou parfois simplement obtenir de l’information dessus. Néanmoins, les attaques permettant de retrouver la clé sont les plus puissantes puisqu’elles permettent à l’attaquant de lire toutes les communications passées et futures auxquelles il ne devrait pas avoir accès. Pour bien se protéger contre l’extraction de clé, il faut avoir une idée précise de ce qu’un attaquant est capable de faire. En effet, les capacités de l’attaquant, et donc la sécurité à apporter, varient beaucoup en fonction du contexte. On distingue trois grands modèles permettant de caractériser le type d’attaquant considéré : la boîte noire, la boîte grise et la boîte blanche. Alors que les deux premiers sont des modèles traditionnels, le troisième, moins connu, est l’objet principal de cet article.

Modèles traditionnels : boîte noire et boîte grise

Le modèle de la boîte noire est le modèle le plus utilisé historiquement. Il définit un attaquant relativement faible qui n’a accès qu’aux entrées et aux sorties de l’algorithme de chiffrement, c’est-à-dire aux messages clairs et chiffrés. Il existe certaines variantes pour cet attaquant : on peut par exemple lui donner ou non la possibilité de demander le chiffrement ou le déchiffrement de messages de son choix. Si même dans ce cas-là il ne peut pas retrouver la clé, on dit que le cryptosystème (c’est-à-dire le système de chiffrement/déchiffrement) est sécurisé dans le modèle de la boîte noire.

Le modèle de la boîte grise considère quant à lui un attaquant un peu plus puissant. En réalité, les chiffrements sont implantés dans des périphériques physiques comme des ordinateurs ou des cartes à puces, ce qui donne des informations supplémentaires. Un attaquant qui aurait volé votre carte bancaire pourrait par exemple analyser le temps d’exécution de l’algorithme ou la consommation de courant de la puce, ce qui peut lui permettre de retrouver la clé secrète si l’implémentation n’est pas protégée.

Prenons l’exemple du chiffrement RSA, l’un des plus utilisés aujourd’hui. Cet algorithme utilisant des calculs modulaires, nous écrirons dans la suite \(x\) mod \(n\) pour décrire le reste de la division euclidienne de \(x\) par \(n\), également appelé résidu modulo \(n\) de \(x\). Le déchiffrement RSA consiste en une exponentiation modulaire, c’est-à-dire que pour récupérer un message \(m\) à partir d’un chiffré \(c\), d’une clé \(d\) sur \(l\) + \(1\) bits et d’un nombre \(n\), on calcule \(m\) = \(c\)^\(d\) mod \(n\) par itérations successives, comme décrit par l’Algorithme 1 ci-dessous. Analyser la consommation de courant de la puce pendant l’exécution de cet algorithme peut permettre à l’attaquant de retrouver la clé. En effet, la consommation de courant d’une puce diffère selon l’opération exécutée. À partir d’une trace, il est donc possible de repérer le motif qui correspond à une mise au carré et celui qui correspond à une multiplication par \(c\). Pour chaque boucle dans l’algorithme, on peut alors savoir si une multiplication a eu lieu et en déduire un bit de la clé.

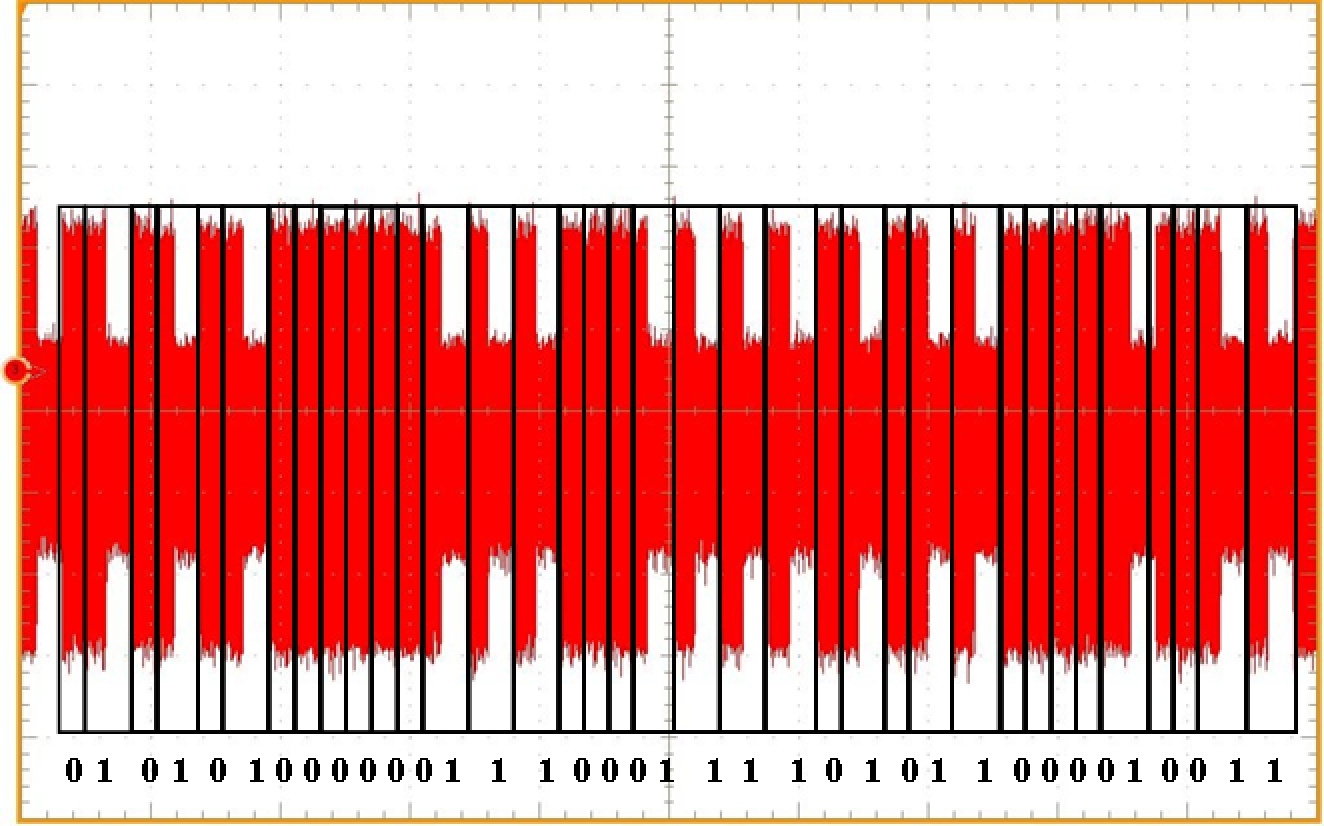Figure 2. Algorithme de déchiffrement RSA (à gauche), trace de consommation de courant et clé associée (à droite).

Ces attaques, qui utilisent des données autres que les messages clairs et chiffrés (cf. Figure 4), sont appelées attaques « par canaux auxiliaires », ou « side-channel » en anglais. Lors de l’implémentation d’un cryptosystème, il est important de connaître ces attaques pour s’en protéger efficacement. Si l’on reprend l’exemple précédent, il suffit de modifier l’algorithme de sorte que les deux opérations soient réalisées à chaque tour de boucle indépendamment du bit de clé, quitte à effectuer des opérations inutiles (cf. Algorithme 2 ci-dessous).

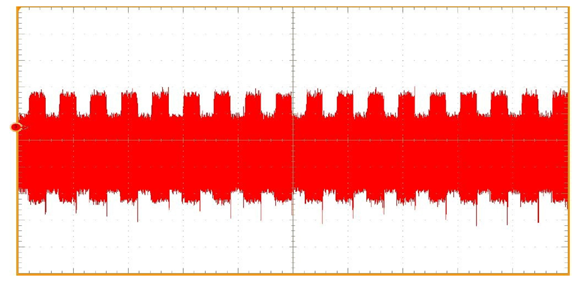Figure 3. Algorithme de déchiffrement RSA en version protégée (à gauche), avec la trace de consommation de courant associée (à droite). La variable inutile sert seulement à se protéger contre les attaques par canaux auxiliaires.

Cette contremesure est efficace contre l’attaque par canaux auxiliaires évoquée plus haut, mais elle ouvre la porte à un autre type d’attaque sur les implémentations. Imaginez que l’attaquant parvienne à perturber l’exécution de l’algorithme au moment où la multiplication de l’itération \(i\) est réalisée. Si le résultat obtenu à la fin du déchiffrement est toujours correct, alors cela signifie que la multiplication était factice et que le \(i\)^e bit de clé valait \(0\). Dans le cas contraire, il valait \(1\). Ces attaques qui consistent à perturber l’exécution sont appelées « attaques par fautes ». Les fautes peuvent être réalisées à l’aide d’un « glitch » (brève modification du courant) ou d’un laser par exemple. Le résultat, que l’on appelle chiffré fauté, est ensuite analysé pour tenter d’en extraire la clé.

Les implémentations qui résistent à la fois aux fautes et aux attaques par canaux auxiliaires sont dites sécurisées dans le modèle de la boîte grise.

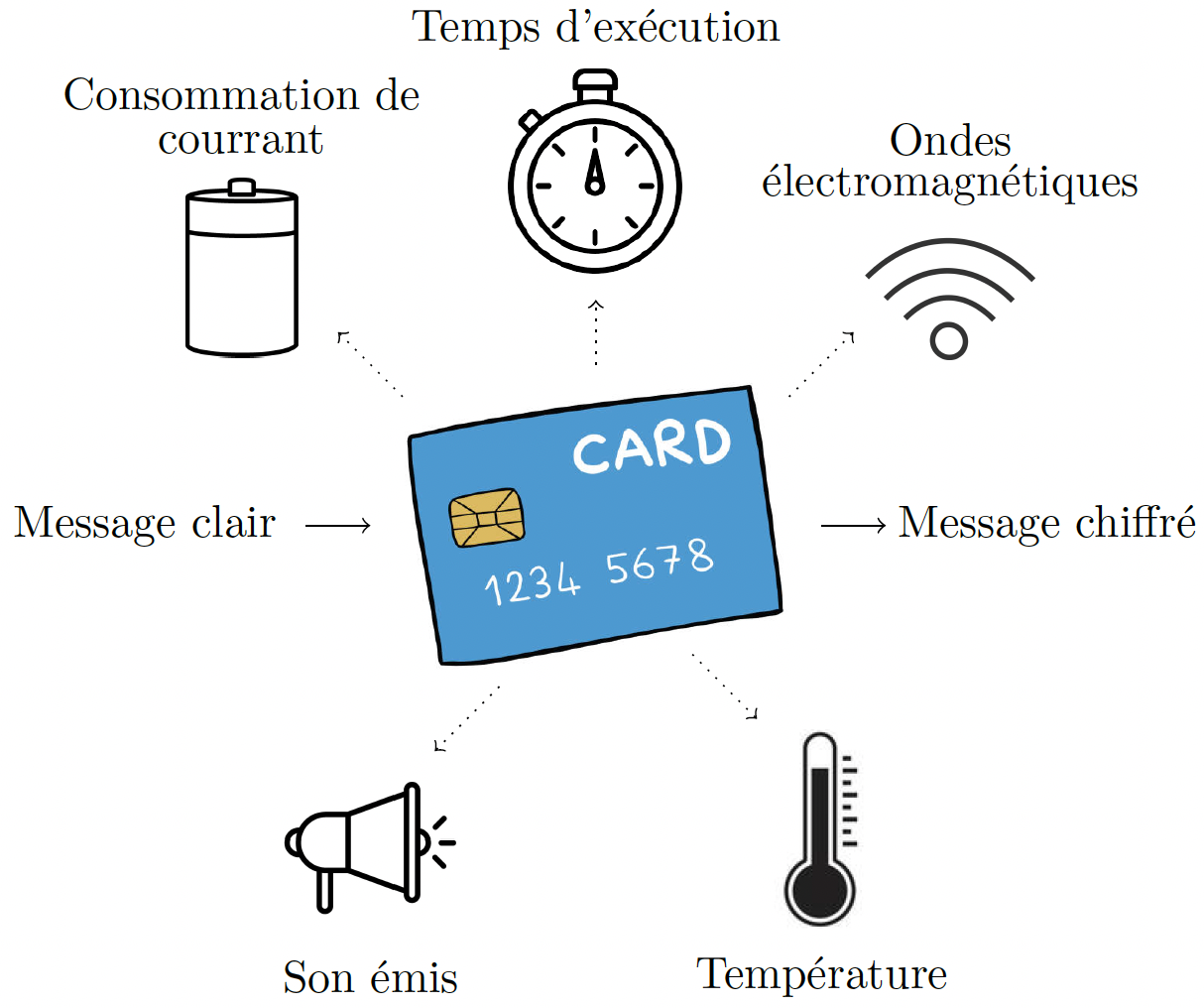
Figure 4. Différents canaux auxiliaires.

Le modèle de la boîte blanche

Contexte

Depuis une vingtaine d’années, nous sommes confrontés à un nouveau modèle, la boîte blanche, qui considère un attaquant encore plus puissant que celui de la boîte grise. Le problème vient du fait que la cryptographie est désormais déployée dans des applications exécutées sur des appareils qui ne contiennent pas nécessairement de matériel sécurisé, comme des smartphones ou des objets connectés par exemple. L’attaquant en boîte blanche a donc potentiellement accès à l’exécutable, qu’il peut lire et même modifier. Il contrôle l’environnement d’exécution et a donc notamment accès à la mémoire utilisée lors de l’exécution. Dans ce contexte, l’implémentation elle-même est la seule ligne de défense contre l’extraction de la clé.

Les cas d’usage typiques pour la cryptologie en boîte blanche incluent les DRM (Digital Right Management) et le paiement mobile. Prenons par exemple le cas d’un film disponible sur une plate-forme de streaming. Bien sûr, la plate-forme ne souhaite pas que n’importe qui puisse lire le film sans avoir payé l’abonnement. Celui-ci est donc chiffré. Pour qu’un utilisateur légitime ait accès au contenu, on pourrait lui donner directement la clé de déchiffrement. Mais dans ce cas là, qu’est-ce qui l’empêcherait de partager cette clé à un ami ou de la revendre ? Il est donc préférable de donner aux utilisateurs légitimes un programme leur permettant de déchiffrer le film sans connaître la clé de déchiffrement. Revendre ce programme s’avère plus compliqué qu’une simple clé. En effet, on peut par exemple faire en sorte qu’il ne fonctionne que sur un périphérique en particulier ou y cacher une donnée qui permettra d’identifier la personne qui l’aura revendu illégalement. Il faut donc empêcher le propriétaire du périphérique de retrouver la clé utilisée.

Dans le cas du paiement mobile, le contexte est un peu différent : le propriétaire de la clé n’a aucun intérêt à ce qu’elle soit divulguée à d’autres personnes. On essaie plutôt de se protéger contre un éventuel virus présent dans le téléphone, qui pourrait transmettre des données à l’attaquant, telles que des valeurs manipulées en mémoire.

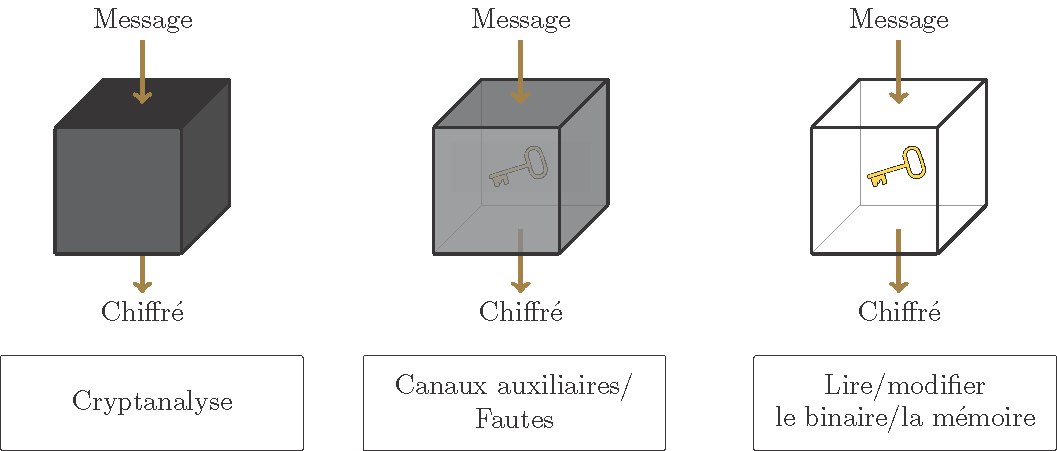
Figure 5. Attaques en boîte noire, boîte grise et boîte blanche.

Attaques héritées du contexte de la boîte grise

Toutes les attaques réalisables dans les modèles de la boîte noire ou de la boîte grise le sont également dans le modèle de la boîte blanche. De plus, les attaques par canaux auxiliaires et les attaques par fautes deviennent plus faciles à réaliser et plus puissantes (voir la référence bibliographique [4]). En effet, pour les attaques par canaux auxiliaires, l’attaquant n’a plus besoin de chercher des moyens détournés pour obtenir de l’information. Au lieu de prendre des traces de consommation de courant par exemple, il peut simplement tracer les valeurs écrites en mémoire ou lues pendant l’exécution. Ainsi, les traces obtenues sont plus précises et les attaques plus efficaces.

Pour les attaques par fautes, plus besoin d’utiliser des glitchs ou des lasers, l’attaquant peut directement modifier l’exécutable ou utiliser des logiciels de débogage (programmes servant à trouver et à analyser des bugs informatiques) pour arrêter l’exécution où il le souhaite et modifier, par exemple, la valeur d’un registre. Les fautes sont donc moins compliquées à réaliser et surtout plus précises.

Au niveau des contremesures, les protections qui fonctionnent en boîte grise sont également utilisables en boîte blanche. Le défi consiste alors à empêcher l’attaquant de les repérer et de les retirer.

Attaques spécifiques à la boîte blanche

Comme expliqué précédemment, un attaquant en boîte blanche contrôle l’environnement d’exécution et peut donc voir les valeurs intermédiaires manipulées en mémoire. Certaines de ces valeurs dépendent de la clé et sont donc sensibles. Une méthode traditionnellement utilisée pour les protéger a été proposée en 2002 par Chow et al. (voir les références bibliographiques [5]et [6]). Nous allons vous en présenter certains aspects.

La première étape consiste à implémenter chaque opération (pouvant être vue comme une fonction) à l’aide de tables, comme suit. Pour chaque entrée possible \(x\) d’une fonction \(F\), on précalcule et on enregistre la valeur \(F(x)\). Lors de l’exécution, plutôt que d’effectuer l’opération, on regarde directement dans la table au bon indice pour trouver le résultat. Cela permet d’éviter que les valeurs intermédiaires manipulées lors du calcul de \(F(x)\) ne soient révélées à l’attaquant. Dans un monde idéal, on pourrait protéger l’intégralité des valeurs intermédiaires en utilisant une seule grosse table qui à chaque message clair associerait un message chiffré. Le problème vient de la taille que prendrait cette table en mémoire. En effet, si les messages clairs sont sur \(128\) bits, alors il y a \(2\)¹²⁸ entrées possibles. La table en question ferait donc des milliards de téraoctets. En pratique, l’implémentation est donc divisée en une multitude de petites opérations prenant un nombre restreint de bits en entrée (souvent \(4\) ou \(8\)), à l’instar d’un circuit qui découpe les entrées pour les traiter par blocs et regroupe ensuite les sorties.

Pour mieux comprendre à quoi cela ressemble, prenons un exemple simplifié. Imaginons que nous voulons cacher les valeurs intermédiaires dans le calcul de la formule

où \(x\)₁ et \(x\)₂ sont les entrées et \(y\) la sortie. Ici, nous avons 4 opérations à implémenter sous forme de tables. Nous les appellerons \(F\)₁ : \(a\) → \(3 × a\) mod \(8\), \(F\)₂ : \(a\) → \(5 × a\) mod \(8\), \(G\) : (\(a, b\)) → \(a + b\) mod \(8\) et \(H\) : \(a\) → \(a + 2\) mod 8 (voir la colonne gauche de la figure 6). Remarquez qu’en l’état, l’implémentation n’est pas encore protégée : un attaquant peut aisément retrouver chaque opération en regardant les tables.

La deuxième étape de la méthode de Chow et al. vise donc à protéger les entrées et les sorties de ces petites tables qui constituent les valeurs intermédiaires, potentiellement sensibles. Le cœur de la technique consiste à leur appliquer des encodages, c’est-à-dire des permutations aléatoires. L’objectif est de mélanger les valeurs de manière aléatoire, un peu comme on mélangerait un paquet de cartes. Bien sûr, pour obtenir le bon résultat à la fin de l’algorithme, il faut faire en sorte que l’encodage en entrée d’une opération soit l’inverse de l’encodage en sortie de l’opération précédente. Ainsi, ces permutations s’annulent entre elles. Seules l’entrée de la première opération et la sortie de la dernière ne sont pas encodées. Le fonctionnement de l’algorithme est donc intact mais toutes les données intermédiaires sont modifiées et non utilisables par un attaquant ne connaissant pas l’encodage utilisé.

Reprenons l’exemple précédent avec la formule \(y\) = \(3x\)₁ + \(5x\)₂ + \(2\) mod \(8\) et imaginons que nous voulons protéger l’implémentation avec les encodages suivants (choisis au hasard) et leurs inverses :

Les tables stockées en mémoire sont alors modifiées comme montré dans la partie droite de la figure 6.

Implémentation non-protégée	Implémentation encodée
Figure 6. Exemple de tables pour l’implémentation de \(y\) = \(3x\)1 + \(5x\)2 + \(2\) mod \(8\). Les valeurs consultées pour le calcul sur les entrées \(x\)1 = \(6\) et \(x\)2 = \(3\) sont écrites en bleu.

Comme annoncé précédemment, le résultat en sortie des deux implémentations est identique pour chaque couple d’entrée (\(x\)₁, \(x\)₂), mais les valeurs intermédiaires sont différentes. Si l’on prend par exemple (\(x\)₁, \(x\)₂) = (\(6\), \(3\)), le résultat est toujours \(3 × 6 + 5 × 3 + 2\) mod \(8\) = \(3\) mais les valeurs intermédiaires valent respectivement \(2, 7, 1\) et \(7, 0, 3\).

En réalité, encoder correctement une implémentation suffit souvent à empêcher l’attaquant de retrouver la clé à partir d’une valeur intermédiaire. Cette technique apporte même une certaine sécurité contre les attaques par canaux auxiliaires et les fautes, bien qu’elle ne soit en général pas suffisante. Pourtant, en théorie, toutes les constructions proposées dans la littérature se basant sur de tels encodages ont été cassées (voir la référence [2]). Ces attaques sont cependant difficiles à mettre en place en pratique et demandent une longue et coûteuse étape de rétro-ingénierie lorsque l’architecture de la boîte blanche n’est pas connue. Les techniques de protection utilisées augmentent donc la sécurité en pratique.

Une approche plus théorique

La cryptographie en boîte blanche est intimement liée à l’obfuscation de code, leur objectif commun étant de protéger les implémentations logicielles. Informellement, un obfuscateur \(O\) est un compilateur qui prend en entrée un programme \(P\) et produit un nouveau programme \(O\)(\(P\)) qui a la même fonctionnalité mais qui est « inintelligible ». En pratique, certains obfuscateurs produisent du code difficilement compréhensible pour un humain. Cependant, ce code reste compréhensible pour une machine et ne masque pas forcément les valeurs intermédiaires pendant le calcul, ce qui n’apporte pas vraiment de sécurité. D’un point de vue théorique, il existe différentes façons de définir ce que pourrait être un obfuscateur rendant les choses vraiment inintelligibles (même pour une machine !). Les deux plus connues sont VBB (Virtual Black Box, ou boîte noire virtuelle en français) et iO (indistinguishability obfuscation). Intuitivement, un obfuscateur VBB produit un nouveau programme \(O\)(\(P\)) qui ne donne aucune information sur le programme original \(P\) qui ne puisse pas déjà être obtenue à partir de ses entrées et sorties. Un obfuscateur iO, quant à lui, produit des programmes indistinguables, c’est-à-dire qu’étant donnés deux programmes \(P\)₁ et \(P\)₂ ayant la même fonctionnalité, et l’obfuscation \(Q\) de l’un d’eux, il est impossible de déterminer si \(Q\) est l’obfuscation de \(P\)₁ ou de \(P\)₂.

La recherche théorique sur l’obfuscation a été lancée par le papier fondateur de Barak et al. (voir la référence [1]) qui montre l’impossibilité de créer un obfuscateur VBB générique. En d’autres termes, il n’existe pas d’obfuscateur qui, pour tout programme donné en entrée, construit une boîte noire virtuelle, pour la simple et bonne raison que certains programmes sont par nature inobfuscables au sens VBB. Cependant, cela n’exclut pas que d’autres programmes soient effectivement obfuscables. Il a d’ailleurs été prouvé que certains programmes simples ont bien un équivalent inintelligible au sens VBB, comme par exemple les fonctions point (pour une certaine constante \(α\), on définit \(f(x)\) = \(1\) si \(x\) = \(α\) et \(f(x)\) = \(0\) sinon, voir la référence [10]).

Saxena et al. (voir la référence [9]) ont fait le lien entre les travaux théoriques sur l’obfuscation et la cryptographie en boîte blanche qui avait seulement été étudiée d’un point de vue pratique jusque là, en utilisant un modèle formel d’attaquant et des notions de sécurité bien définies. Du côté négatif, ils ont prouvé que pour toute famille de fonctions « intéressantes » (dans un certain sens), il existe des notions de sécurité pouvant être atteintes dans le modèle de la boîte noire mais pas en boîte blanche. Du côté positif, ils ont montré qu’il existe une boîte blanche pour un cryptosystème spécifique (inventé pour l’occasion) et une notion de sécurité précise (IND-CPA). Ce cryptosystème n’est pas très utile en pratique, mais ces résultats ont une portée théorique intéressante.

D’autres notions de sécurité ont par la suite été formalisées par d’autres auteurs, notamment Delerablée et al. (voir les références [7]) et Alpirez Bock et al. [3]), qui se sont aussi intéressés au lien entre boîte blanche et obfuscation. Cela a mené à de nouvelles propositions de boîtes blanches pour lesquelles certaines notions de sécurité ont pu être prouvées (voir la référence [8]).

Une piste à creuser

Malgré un nombre important d’applications pratiques, le modèle de la boîte blanche est encore assez peu étudié. Les constructions en boîte blanche de cryptosystèmes standards proposées dans la littérature scientifique sont régulièrement cassées et l’existence même d’une solution efficace est incertaine. La recherche s’est donc scindée en deux axes complémentaires. D’un côté, trouver des contremesures concrètes et applicables contre les attaques connues sur les cryptosystèmes standard. De l’autre, étudier ces questions d’un point de vue théorique, en tentant d’obtenir des garanties mathématiques de sécurité, quitte à s’intéresser d’abord à des cryptosystèmes non standard ou à des solutions moins réalistes.