Sciences de l’information : là où le temps sous-tend tant et tant

Prenons donc le temps de regarder deux facettes du temps :

• Temps logique, relatif, d’aucuns diront « temps de calcul », c’est bien ce concept de temps qui permet à un logiciel d’aller là où on l’attend.
• Temps physique, absolu, mesurable plus ou moins finement, ce concept-là est utilisé notamment pour le traitement du signal.

1. Premier temps : le temps qui défie l’informatique

© Inria / Photo Jim Wallace

La notion du temps est intrinsèquement liée à l’informatique, puisqu’il est vite apparu que presque tous les calculs étaient possibles, mais que voilà… ils pouvaient durer incommensurablement longtemps ! Ainsi, à énumérer tous les cas possibles pour effectuer une opération, cela peut durer tant et tant… qu’au bilan, on aura perdu son temps.

Temps de calcul : entre jamais et trop longtemps

Les mécanismes de base de l’informatique sont les algorithmes. C’est par le nombre d’opérations élémentaires à exécuter pour réaliser la tâche qui a permis de les spécifier qu’est défini le temps de calcul. Ainsi, l’exemple suivant :

où la variable x prend la valeur 5 et y vaut 6, nécessite deux additions et deux affectations. (La valeur correspondant au résultat de la première addition est affectée à x, celle de la seconde à y). En tout, quatre opérations sont exécutées. De même, trier un tableau de n éléments nécessite un nombre d’opérations qui augmente avec n. Pour les algorithmes de tri peu évolués, ce nombre d’opérations est proportionnel à n² (le carré de n). Les algorithmes de tri les plus malins se contentent d’augmenter en n log₂n. Prenez l’annuaire téléphonique francilien : 10 millions d’entrées. La différence est énorme : les tris les plus malins utiliseront de l’ordre de 100 millions d’opérations (c’est beaucoup mais jouable) ; les autres plus de 100 mille milliards ! (là c’est perdu d’avance). À grande échelle, le temps se multiplie vite.

Où le temps explose

Mais il y a pire, la complexité algorithmique est parfois exponentielle. Un exemple concret permet de l’illustrer. Imaginons qu’une compagnie d’électricité cherche à déterminer le chemin le plus court pour relever les compteurs dans un petit village un peu tarabiscoté. À chaque carrefour, le releveur aura au minimum deux choix, disons donc pour simplifier qu’il en a deux (même si dans la réalité ce serait souvent un peu plus). Comment faire ? Eh bien, il suffit de faire partir plusieurs releveurs en même temps, un groupe de T releveurs, et à chaque carrefour, une partie du groupe ira à gauche, l’autre à droite et ainsi de suite, jusqu’à ce que le releveur (ou le groupe) le plus chanceux (celui qui de choix en choix aura pris le chemin le plus court) arrive au bout du parcours le premier et envoie un message à tous les autres : j’ai fini les amis ! Quel algorithme apparemment fructueux : il est si simple, et puis il va vite ! Avec un nombre T de releveurs suffisamment grand, nous avons résolu le problème (grâce au releveur le plus chanceux) en un temps égal au trajet le plus court. Merveilleux ? Presque. Où est le hic ? Le nombre T de releveurs ! Eh oui, si le village compte L carrefours et que le choix (simplifié) est binaire (partir à gauche ou à droite), le nombre de releveurs qu’il faudra au départ sera au moins de 2 x 2 x 2… x 2 (ceci L fois), sinon à un carrefour donné un releveur sera tout seul et ne pourra aller à la fois à gauche et à droite. Bref, il faut au moins : T > 2^L releveurs, et c’est énorme. S’il y a 10 carrefours, cela fait un peu plus de 1000 releveurs ; avec 100 carrefours (Paris en compte bien plus), plus de 1000 000 000 000 000 000 000 000 000 000 releveurs. Ingérable. Mais très riche en enseignement. C’est bien à cause de ce genre de problème que des algorithmes plus élaborés ont été proposés pour trouver le plus court chemin.

Complexité polynomiale et exponentielle

Un algorithme de tri a une complexité qui augmente avec la taille du problème, mais sans « exploser », c’est une complexité polynomiale. L’algorithme du plus court chemin tel que décrit précédemment a lui une complexité qui explose très vite en augmentant, une complexité exponentielle (la taille du problème L est en exposant). Le temps de calcul est explosif.

Et la très mauvaise nouvelle est que de nombreux problèmes intéressants à résoudre sont hélas exponentiellement compliqués (notamment tous les problèmes de recherche opérationnelle, qui consistent à chercher la meilleure solution d’un problème où il faut combiner des éléments : file d’attente, ordonnancement, etc.). On observe même un tel phénomène de complexité combinatoire dans un jeu aussi simple que le sudoku.

Complexité et taille mémoire

Comment simuler mes T releveurs sur un unique ordinateur ? En gardant en mémoire l’état de chaque releveur (ici le chemin qu’il a parcouru) et en simulant pour chacun tour à tour le fait qu’il arrive à un carrefour puis choisisse d’aller à gauche ou à droite, etc. Facile, mais… mais cela signifie qu’il faudra une taille mémoire qui elle aussi augmente proportionnellement à T. Le temps de calcul sur mon ordinateur unique va augmenter proportionnellement au nombre T de releveurs et proportionnellement au nombre de carrefours L. Au-delà de cet exemple, le lien entre temps de calcul et taille mémoire est parfois complexe. Plus le problème est compliqué, plus la taille mémoire et le temps de calcul augmentent (ici exponentiellement). En revanche, dans d’autres cas, garder en mémoire les résultats intermédiaires pour ne pas les recalculer limite le temps de calcul.

En pratique, les algorithmes sont analysés et modifiés de façon à minimiser le nombre d’opérations et d’accès mémoire. Pour diminuer les accès mémoire, il suffit parfois de changer l’ordre des calculs dans une boucle, ou d’utiliser judicieusement le contenu de la mémoire cache de la machine en chargeant à l’avance les données qui vont être utilisées dans les calculs à venir.

Un exemple classique de ce type d’astuce est l’implantation rapide de la transformée de Fourier discrète (FFT, pour Fast Fourier Transform). Un tel travail est nécessaire pour implanter efficacement un algorithme dans une architecture de calcul dédiée (comme les circuits de type FPGA ou Field Programmable Gate Array, qui sont des réseaux de circuits logiques à connexions programmables), ou même dans un processeur de signal (DSP). En effet, il faut non seulement implémenter le calcul le plus rapidement possible, mais aussi de manière suffisamment simple (avec une liste d’instructions spécifiques) pour qu’il puisse s’exécuter efficacement sur des architectures dédiées. Chercher une telle optimisation n’est certes pas sans risque.

Il y a toujours un compromis à faire entre temps de calcul et mémoire. C’est le cas tout particulièrement pour les algorithmes récursifs ou en programmation synchrone, dont il est question plus loin.

Complexité et parallélisme

Imaginons que plusieurs ordinateurs puissent fonctionner en parallèle, chacun simulant une partie de mes T releveurs. Cela va aller plus vite. Certes. Mais pas énormément. Car il faudrait ici un nombre exponentiellement grand d’ordinateurs, plus que le nombre total d’ordinateurs jamais construits. Le parallélisme est très utile pour économiser du temps de calcul pour des problèmes de complexité polynomiale, c’est beaucoup moins simple si elle est exponentielle. C’est même aujourd’hui un enjeu international sur les grilles informatiques.

Pour en savoir plus sur le parallélisme, nous vous proposons de télécharger un cours de l’École polytechnique sur ce sujet, disponible en PDF (1 Mo).

Pourtant, des systèmes physiques pourraient permettre de briser cette barrière de la complexité : les ordinateurs quantiques. Dans ce cas, un nombre justement exponentiellement grand d’opérations élémentaires pourraient être effectuées simultanément, ainsi certains problèmes explosifs deviendraient… raisonnablement compliqués.

Être sûr qu’un temps de calcul est exponentiellement compliqué n’est pas forcément une malédiction : c’est l’inverse dans le cas de la cryptographie. Quand vous protégez vos données avec un mot de passe, vous êtes acquis à l’idée que tout le monde pourra y accéder, pourvu qu’il ait la chance de tomber sur le bon mot de passe, ou qu’il essaie toutes les possibilités. C’est bien le fait qu’essayer toutes les possibilités prend du temps (un temps de calcul explosif) qui protège vos données. Un exemple historique, la machine Enigma, illustre bien ce fait.

Où le temps devient infiniment grand

Le temps de calcul peut être encore pire qu’explosif… il peut être infini !

Voici un exemple tout à fait idiot :

Pour cette opération, x vaut d’abord 1, puis tant qu’il est supérieur à 0, ce qui reste toujours le cas, il va augmenter de 1, etc. Et l’opération ne s’arrêtera jamais… jusqu’à ce que la valeur devienne suffisamment grande pour bloquer le calcul !

Faut-il être bête pour écrire un algorithme pareil. Certes. Mais combien de fois votre ordinateur familial ne s’est-il pas bloqué indéfiniment sur une boucle aussi idiote que celle-ci sûrement, mais d’une complexité inouïe à détecter… car ce n’est pas un algorithme d’une ligne, mais des centaines de milliers de lignes d’algorithmes qui font tourner votre ordinateur ! Détecter ces « boucles » est un problème un peu plus que compliqué !

Comme pour le problème de notre releveur de compteurs, il faut sûrement explorer tous les cas possibles, cela semble donc exponentiellement compliqué. En un sens oui. Mais là nous parlons de boucle infinie, donc explorer « tous » les cas possibles conduit à explorer… un espace sans limite. C’est un problème indécidable.

Cette notion, point dur en sciences de l’information, a été formalisée il y plus d’un demi-siècle par un logicien : Gödel. Elle est au cœur des problèmes les plus intenses de cette science.

S’assurer qu’un algorithme général ne bouclera pas est un problème indécidable, pour concevoir des logiciels sûrs il faut alors se mettre dans un cadre plus précis, où toutes les opérations ne sont pas permises. Démontrer qu’un algorithme va réaliser l’opération souhaitée dans un temps imparti est un problème crucial (par exemple en chirurgie assistée par ordinateur) mais hélas, indécidable. Il a été pourtant résolu dans des cas précis.

Beaucoup de problèmes de décisions sont semi-décidables : si la réponse est « non », alors la réponse se trouve en temps fini, si la réponse est « oui », alors impossible de s’en assurer, sauf à exécuter un algorithme dont le temps de calcul est infiniment long. Pour avoir tort, c’est facile, il suffit de se tromper, mais pour avoir vraiment raison, il faut attendre un temps illimité, puisqu’un contre-exemple pourra toujours surgir inopinément. Cet état de fait, présenté ici en une phrase, correspond à un raisonnement rigoureux.

Informatique en temps réel : rien ne sert d’aller vite, il faut juste être à temps

Beaucoup de problèmes informatiques pratiques se résolvent fort heureusement sans exploser en temps. On parle alors de temps réel, pour dire que le résultat du calcul va arriver à temps.

L’exemple le plus célèbre est celui de la prédiction des phénomènes météorologiques où il y a quelques années déjà le temps du lendemain matin était prédit avec précision… en trois jours de calcul ! Dans ce cas, c’est la technologie qui a permis de gagner sur le temps. Avec la loi de Moore, le temps de calcul augmente assez vite pour rendre possible ce qui ne l’était pas hier, sans toutefois oublier les grands problèmes cités précédemment. Mais ne nous trompons pas : la clé de la performance n’est pas essentiellement technologique.

Ce sont des méthodes modernes d’analyse statique de pire temps d’exécution de programmes qui permettent aujourd’hui de s’assurer de la performance de tel ou tel calcul.

De même, les traitements qui réclament de très grands calculs comme l’exploration et l’analyse des textes des génomes sont rendus possibles tant par l’augmentation de la vitesse des processeurs que par les progrès de l’algorithmique qui propose des méthodes de plus en plus performantes.

Robot marcheur BIP. Le but n’est pas de reproduire le fonctionnement du corps humain, ce qui dépasserait les capacités de la technologie actuelle, mais de reproduire les principales caractéristiques du système locomoteur. © Inria / Photo Jim Wallace

L’interaction avec un automatisme, par exemple un système robotique, est rendue possible uniquement si le temps de calcul peut-être très précisément borné, c’est le temps réel au sens strict. Les méthodes de programmation synchrone permettent de garantir non seulement le résultat du calcul, mais aussi l’instant où ce résultat sera disponible. Pour cela, tous les choix possibles ont pu être prévus à l’avance, mémorisés, ce qui conduit à un algorithme qui réagit quasiment sans délai. On parle d’automate à états finis, et les transitions d’un état à un autre ont été compilés dans une table. On est dans un cas limite où l’espace mémoire permet de gagner sur le temps. Les théoriciens de ces méthodes supposent d’ailleurs que l’ordinateur réagit… infiniment vite ! D’où le nom de synchrone. Et cette simplification, finalement bien réaliste dans ce contexte, leur permet de déduire beaucoup de propriétés temporelles très importantes pour garantir des logiciels sûrs. Ces recherches théoriques, non seulement permettent de garantir le temps, mais aussi, grâce au cadre logique rigoureux, de garantir d’autres propriétés sémantiques.

Pour en savoir plus sur la programmation synchrone, vous pouvez télécharger le rapport de recherche fondateur, disponible en PDF (1 Mo).

Temps réel ne veut pas forcément dire « aller vite » : interagir avec un utilisateur nécessite des temps de réaction de quelques dizaines de millisecondes, avec un système mouvement de quelques centaines de microsecondes, avec un système végétal de plusieurs minutes. Non seulement l’échelle de temps varie, mais sa précision aussi : dans le réseau internet, des temps d’attente sporadiques sont acceptables, en informatique médicale, c’est inenvisageable.

Par de nombreux aspects, le temps est présent dans les travaux de recherche en sciences de l’information, à des échelles très différentes. La simulation de la croissance des plantes, où il faut modéliser l’évolution au cours de très longues périodes de temps, en est un exemple extrême. Lors de l’analyse du mouvement au niveau de la perception visuelle, les variables liées au temps, comme la vitesse, deviennent l’objet même de l’étude.

2. Second temps : le temps qui s’égrène

© PhotoAlto / Photo Philippe Ughetto

En traitement du signal et des images, le temps est une variable usuelle. En effet, les signaux manipulés par de nombreux systèmes de traitement de l’information dépendent du temps. C’est le cas de signaux audiofréquences reçus sur un microphone, de signaux reçus par un capteurs GPS, de signaux hyperfréquences émis et reçus par un téléphone portable, de signaux biomédicaux enregistrés en électrocardiographie ou en électroencéphalographie, etc. C’est aussi le cas de l’enregistrement de séquences d’images vidéo.

Synchronisation : le temps qui tombe au bon instant

Dans les dispositifs électroniques, la mesure du temps est faite localement à l’aide d’horloges électroniques pilotées par des quartz. Les fréquences sont très élevées et très précises, mais il peut y avoir des fluctuations (par exemple dues aux variations de température) et des différences de phase. Le temps est mesuré en comptant les impulsions d’horloge : de petites fluctuations sur la fréquence d’horloge peuvent conduire à des erreurs de temps importantes, dès lors que les erreurs sont accumulées sur un grand nombre d’impulsions. De plus, avec les dispositifs mobiles (parfois à très grande vitesse : avion ou TGV), les fréquences des signaux reçus sont modifiées par effet Doppler.

Pour bien mesurer ces problèmes, regardez :

• la mesure de la distance Terre-Lune ou de la dimension de la Terre par triangulation nécessitait de synchroniser parfaitement l’instant de la mesure entre deux lieux distants de plusieurs centaines de kilomètres ;
• en navigation GPS, la localisation d’un objet demande que les horloges des satellites soient synchronisées : une erreur de temps sur un satellite entraîne une erreur de positionnement au sol, et des incohérences avec les mesures des autres satellites ;
• en téléphonie mobile, les messages sont des suites de symboles binaires (0 et 1) dont la durée est égale à la largeur symbole ; l’interprétation correcte exige que le récepteur se synchronise sur le début de chaque mot et de chaque symbole ;
• dans un enregistrement vidéo, les modalités son et image sont codées et enregistrées différemment, et doivent être synchronisées.

Dans les systèmes biologiques, il existe également des horloges. Outre les rythmes régis par le jour et la nuit (qui nous causent par exemple les problèmes de décalage horaire), dans le cerveau des vertébrés, on observe des circuits dits « pacemakers », qui délivrent des séries régulières d’impulsions. Les systèmes de poursuite de cibles, chez la mouche grâce à son œil à facettes, ou chez la chauve-souris grâce à son sonar, sont des exemples où la localisation et la distance sont appréciées par des décalages temporels, selon des principes d’inter-corrélation.

Temps et fréquence : inverser le temps quand les rythmes décrivent le temps

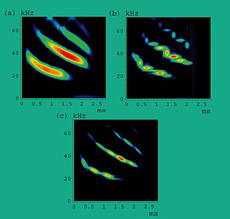
Trois représentations temps-fréquence d’un son complexe (ici un cri de chauve-souris, aimablement fourni par C.Condon, K.White et A.Feng du Beckman Institute de l’Université de l’Illinois). © Inria / CNRS – Image équipe METISS

La notion de temps est intimement liée à la notion de fréquence. Cette relation apparaît dans le fait qu’une horloge donne un signal périodique de période T et de fréquence f = 1/T. En traitement du signal, la dualité entre le temps et la fréquence apparaît via la représentation de Fourier d’un signal : à un signal x(t) est associé (sous certaines conditions) son spectre X(f), et on peut passer d’une représentation à une autre sans perte d’information : les deux représentations sont donc équivalentes. En particulier, l’énergie est conservée entre les deux représentations.

Cette dualité temps-fréquence est aussi associée au principe d’incertitude. Pour bien localiser l’énergie d’un signal en temps, il faut une durée T petite ; pour bien localiser son énergie en fréquence, il faut choisir une durée T plus longue, théoriquement tendant vers l’infini si la fréquence devient une fréquence unique. On retrouve ce principe dans cette dualité temps-fréquence :

• un signal infiniment court (une impulsion) a un spectre infiniment étendu (toutes les fréquences y contribuent),
• une fréquence pure (un spectre constitué d’une seule raie) est associée à un signal de durée infinie. En effet, si le signal s’arrête (ou commence) à un instant t, il y a un transitoire qui contient une infinité de fréquences.

C’est le paradoxe de la mécanique quantique, où on ne peut pas localiser parfaitement une particule, mais seulement lui attribuer une probabilité d’être à un endroit donné à un instant donné.

Temps de propagation et temps d’accès : comment éviter d’attendre trop longtemps

Les dispositifs électroniques traitent les informations en binaire. Les tensions électriques associées aux signaux doivent avoir le temps de s’établir et d’être stables. Compte tenu des propriétés électriques des entrées et sorties des circuits électriques, l’établissement nécessite de quelques picosecondes à quelques nanosecondes (selon la vitesse des circuits). Pour une mémoire, le temps d’accès est lié à la somme du temps nécessaire pour forcer l’adresse de l’information, et de celui de la lecture du contenu de la mémoire. De la même manière, sur un disque dur ou un lecteur de CD ou DVD, l’accès à une piste puis à un secteur demande au préalable le positionnement mécanique des têtes de lecture, ce qui limite le temps d’accès à l’information.

En comparaison, le cerveau (humain ou animal) semble résoudre ce genre de problème de manière époustouflante.

La durée d’exécution d’un programme dépendra des accès mémoire (ou disque), mais aussi énormément du nombre d’opérations. Mais on rejoint ici le domaine du temps relatif, déjà évoqué plus haut.

Ces problèmes sont particulièrement critiques en vidéosurveillance ou pour des dispositifs d’interaction Homme-machine.

Échantillonnage : quand l’ordinateur doit saucissonner le temps

Les signaux traités par les machines (téléphone, lecteur MP3 ou DVD) sont échantillonnés, c’est-à-dire qu’ils ne sont mesurés qu’à certains instants, généralement espacés régulièrement selon une période d’échantillonnage Te. Pour que le signal soit reproduit fidèlement, il faut que la période soit suffisamment faible. Ici encore, la dualité temps-fréquence apparaît : un théorème, dû à Shannon en 1949, indique que la fréquence 1/Te associée à la période d’échantillonnage Te doit être supérieure au double de la fréquence maximale contenue dans le signal, notée f_max.

Dans les dispositifs de transmission du signal, on peut transmettre des paquets d’échantillons à des fréquences beaucoup plus élevées, mais la restitution devra être faite à la bonne cadence pour ne pas distordre le signal. Si des échantillons sont perdus, ou si leur valeur semble bizarre, on peut ainsi calculer très rapidement des valeurs de remplacement (par interpolation, par exemple), pourvu d’être capable de restituer le signal à la bonne cadence : c’est le principe utilisé dans les correcteurs numériques des lecteurs de CD et DVD.

De même, lors de la résolution et de la simulation de systèmes continus sur un ordinateur, à l’aide d’une équation échantillonnée de la forme X(t + dt) = F(X(t)), le problème du choix du pas de discrétisation (le pas de temps noté dt) génère cette recherche de compromis entre rapidité de calcul et précision. La façon d’échantillonner (très rapide mais rudimentaire, ou au contraire plus sophistiquée, au risque d’être trop longue à calculer) est un élément de cette dualité.

Ce problème est l’un de ceux rencontrés pour la modélisation des ondes sonores et de leur propagation, par exemple dans le cas de la guitare acoustique.

Stationnarité et ergodisme : que dire quand l’aléa se mêle au temps

En traitement du signal, les observations sont souvent perturbées par des signaux indésirables que l’on appelle des bruits (par exemple, le bruit de fond d’un amplificateur ou du téléphone). Ces signaux aléatoires ne peuvent pas être décrits simplement par un modèle mathématique déterministe (comme une fonction sinus par exemple), et on les caractérise par des paramètres statistiques.

On suppose souvent que les caractéristiques ne varient pas dans le temps : c’est l’hypothèse de stationnarité. En fait, cette hypothèse n’est vraie que sur un intervalle de temps : un signal réel a une durée finie, et ses propriétés changent souvent au cours du temps. Par exemple,

• un signal de parole est une suite de sons voisés (voyelles) et non voisés (consonnes) et de silences : l’énergie du signal disparaît dans les moments de silence, c’est une première forme de stationnarité ; pendant la production d’un son, l’énergie peut être localisée autour de quelques fréquences privilégiées (les « formants » pour les sons voisés) ou un peu partout pour les sons non voisés (par exemple pour les « fricatives », comme f, s, etc. ;
• en télécommunications, le signal reçu par votre téléphone mobile dépend du message émis et du canal de propagation entre l’antenne de l’émetteur et votre récepteur : si vous êtes dans le TGV, le canal change très vite et la forme du signal reçu aussi. Si vous marchez en ville, en raison des réflexions des ondes sur les immeubles, le canal change aussi, ainsi que le signal reçu. Ce canal de propagation, et par conséquent le signal reçu, sont a priori non stationnaires.

Lorsque les signaux sont non stationnaires, de nombreux traitements n’ont un sens que sur de petites fenêtres temporelles sur lesquelles le signal est à peu près stationnaire. Pour des signaux de parole, ce sera environ 20 millisecondes ; pour le canal d’un mobile, de l’ordre de la milliseconde à quelques secondes, selon l’environnement et la vitesse de déplacement.

Les propriétés des bruits devraient théoriquement être mesurées en calculant des moyennes statistiques (espérances mathématiques) sur une infinité de réalisations. Par exemple, pour caractériser le bruit de fond d’un amplificateur, on devrait faire la moyenne statistique des caractéristiques d’un très grand nombre d’amplificateurs (en théorie, une infinité). Bien sûr, ceci est impossible, et même en se restreignant à un grand nombre de machines, cela coûterait très cher et demanderait beaucoup de temps. Si le système est supposé ergodique, on postule que la moyenne statistique est égale à la moyenne temporelle. Cette dernière est facile à calculer, au moins de manière approchée : pour qu’une moyenne ait un sens, il suffit de mesurer le signal sur un unique dispositif pendant un temps suffisamment long. Cette hypothèse est à la base de nombre de mesures et de méthodes en théorie du signal.

Il faudrait plus de temps pour parler de tous les temps

Il est un autre aspect tout aussi important : c’est que l’usage généralisé de l’informatique a changé notre vécu du temps. Avec les systèmes d’informations interconnectés au niveau planétaire, abolissant les distances, le temps s’est fortement rétréci. En mathématiques financières , il est clair que l’informatisation des bourses peut conduire à des effets de réactivité extrêmement raccourcis. Nos emplois du temps se modifient quand les achats et démarches administratives se font sur internet presque instantanément. Ou quand une visioconférence remplace de longs déplacements. Les technologies de l’information ont pareillement un fort impact sur l’enseignement. La conférence de Michel Serres disponible sur ce site donne des pistes de réflexions profondes sur l’impact sociétal des sciences de l’information.

Il nous faudra sûrement un peu de temps pour mesurer combien cela influence notre temps, le temps présent.