Lire la partition de la nature grâce au programme de Fourier

Plus que des formules, un véritable programme

Joseph Fourier est à l’origine des séries et transformée du même nom dont les formules et modalités d’utilisation causent parfois bien du tracas aux étudiants qui les découvrent durant leur cursus. Cependant, pour reprendre les propos du regretté Jean-Pierre Kahane, véritable héraut de l’Analyse dite de Fourier, dans son discours à l’Académie des sciences intitulé Le retour de Fourier (Août 2005) :

La portée réelle des formules de Fourier apparaît aujourd’hui mieux que naguère : elles constituent un programme. On peut varier le sens que l’on donne aux fonctions, aux séries et aux intégrales. Il s’agit dans tous les cas d’analyse et de synthèse harmonique. C’est le travail des mathématiciens que d’introduire les concepts et les outils qui valident les formules.

De fait, l’Analyse de Fourier est aujourd’hui une branche vivante aussi bien au sein des mathématiques que de la physique, à l’instar du traitement du signal comme l’évoque Patrick Flandrin de l’Académie des sciences dans Le traitement du signal, au cœur de la science et de notre vie quotidienne (The Conversation, 2017). Si le panthéon scientifique compte nombre de géants, rares sont ceux qui peuvent se targuer d’une telle actualité.

Ainsi en parle Cédric Villani, médaille Fields 2010 et président d’honneur du comité Fourier 250 qui coordonne les commémorations nationales du 250^e anniversaire de Joseph Fourier, dans son livre Théorème Vivant (2012) :

L’analyse de Fourier sert à tout : à analyser les sons et à les graver sur un CD, mais aussi à analyser les images et à les transmettre par Internet, ou à analyser les variations du niveau de la mer et à prédire les marées […] l’influence de Joseph Fourier est maintenant bien plus importante que celle de Hugo lui-même ; son « grand poème mathématique » (comme disait Lord Kelvin), enseigné dans tous les pays du monde, est utilisé chaque jour par des milliards d’humains qui ne s’en rendent même pas compte.

Quelques applications modernes de l’Analyse de Fourier (crédit : Claudia Théry)

Décrypter le langage de la nature

Si les outils dits de Fourier sont déjà présents dans les écrits de Joseph Fourier datant de la première décennie du XIX^e siècle, sa grande œuvre La théorie analytique de la chaleur n’est intégralement éditée qu’en 1822.
Revenons ainsi à Fourier lui-même pour qui l’étude de la nature est la source la plus féconde des découvertes mathématiques. Écoutons-le parler du lien entre l’analyse mathématique et les phénomènes naturels :

[…] cette science difficile se forme avec lenteur, mais elle conserve tous les principes qu’elle a une fois acquis ; elle s’accroît et s’affermit sans cesse au milieu de tant de variations et d’erreurs de l’esprit humain. Son attribut principal est la clarté. Elle n’a point de signes pour exprimer les notions confuses. Elle rapproche les phénomènes les plus divers, et découvre les analogies secrètes qui les unissent. Si la matière nous échappe comme celle de l’air et de la lumière par son extrême ténuité, si les corps sont placés loin de nous, dans l’immensité de l’espace, si l’homme veut connaître le spectacle des cieux pour des époques successives que sépare un grand nombre de siècles, si les actions de la gravité et de la chaleur s’exercent dans l’intérieur du globe solide à des profondeurs qui seront toujours inaccessibles, l’analyse mathématique peut encore saisir les lois de ces phénomènes. Elle nous les rend présents et mesurables, et semble être une faculté de la raison humaine, destinée à suppléer à la brièveté de la vie et à l’imperfection des sens ; et ce qui est plus remarquable encore, elle suit la même marche dans l’étude de tous les phénomènes ; elle les interprète dans le même langage, comme pour attester l’unité et la simplicité du plan de l’univers, et rendre encore plus manifeste cet ordre immuable qui préside à toutes les causes naturelles.

Pour décrypter le langage de la nature, Fourier déroule donc un véritable programme qui fait la part belle à la dimension opérative : « on perfectionnera les instruments et l’on multipliera les expériences ». Il insiste aussi sur le fait d’approfondir les méthodes de calcul « jusqu’aux dernières applications numériques, condition nécessaire de toute recherche, sans lesquelles on n’arriverait qu’à des transformations inutiles ». Rappelons que Fourier est à l’origine de quelques notations symboliques aussi utiles qu’incontournables telles celles des bornes de sommation ou d’intégration ainsi que quelques notions aussi fondamentales que celle de flux.

Ce genre de philosophie, préfigurant l’approche moderne qui combine modélisation, incessants allers-retours théorie-pratique et calcul scientifique, n’était pas du goût de tous. Peu de temps après la mort de Fourier, le mathématicien Jacobi écrivait ainsi à son confrère Legendre :

Il est vrai que M. Fourier avait l’opinion que le but principal des mathématiques était l’utilité publique et l’explication des phénomènes naturels ; mais un philosophe comme lui aurait dû saisir que le but unique de la science, c’est l’honneur de l’esprit humain, et que sous ce titre, une question de nombres vaut autant qu’une question de système du monde.

Cette dernière conception, opposant mathématiques pures et appliquées, régnera sans partage durant près de 150 ans, atteignant son apogée au XX^e siècle, sous la domination du groupe Bourbaki. L’un de ses membres les plus emblématiques, le mathématicien Jean Dieudonné, écrira un livre intitulé Pour l’honneur de l’esprit humain (1987), ouvrant celui-ci sur la célèbre citation de Jacobi. Cette époque est révolue.

Revenons donc au décryptage de l’unité et de la simplicité du plan de l’univers, simplicité qui étonnera Albert Einstein un siècle plus tard : « ce qui est incompréhensible, c’est que le monde soit compréhensible ». Enfonçons le clou avec les mots du mathématicien et philosophe Henri Poincaré : « La Théorie de la Chaleur de Fourier est un des premiers exemples d’application de l’analyse à la physique […]. Les résultats qu’il a obtenus sont certes intéressants par eux-mêmes, mais ce qui l’est plus encore est la méthode qu’il a employée pour y parvenir et qui servira toujours de modèle à tous ceux qui voudront cultiver une branche quelconque de la physique mathématique. »

Dès le départ, Fourier est conscient de l’universalité de son héritage : « Les équations du mouvement de la chaleur, comme celles qui expriment les vibrations des corps sonores, ou les dernières oscillations des liquides, appartiennent à une des branches de la science du calcul les plus récemment découvertes. » Joseph Fourier est le « créateur de la physique mathématique » comme en témoigne le titre de l’ouvrage que Jean Dhombres, mathématicien et historien des sciences, lui a consacré.

Langage ou musique ?

Si les vibrations des corps sonores arrivent juste après l’équation de la chaleur, domaine d’application choisi pour l’emploi de sa « méthode », ce n’est probablement pas un hasard. Fourier connaît l’importance depuis Pythagore (VI^e siècle avant Jésus-Christ) du problème de la vibration d’une corde tendue, suite par exemple à un pincement. L’analyse mathématique s’est développée de concert avec l’étude du problème de la corde vibrante, jusqu’à Fourier qui s’y pencha aussi, posant notamment la question de la nature de ce que nous appelons une fonction. La mathématicienne Sophie Germain, première femme à obtenir le prix de l’Académie des sciences, protégée de Fourier, a porté son intérêt sur le problème de la vibration des surfaces dites élastiques, telles que celles d’un tambour. Au passage, Joseph Fourier était un grand éveilleur et protecteur de talents : que ce soit avec Louis Vicat, père des ciments artificiels, ou encore avec le jeune Champollion en Isère, déchiffreur des hiéroglyphes, qui se fera enterrer au Père-Lachaise auprès de son héros Fourier qui, rappelons-le, est aussi un des pères de l’Égyptologie scientifique en langue française.

Ici, l’expérimentateur fait vibrer une plaque sur laquelle est déposé du sable fin grâce à un archet. Des figures dites de Chladni (1756-1827) apparaissent. Photo : Matemateca IME-USP / Rodrigo Tetsuo Argenton, CC-BY-SA 4.0 via Wikimedia commons

L’Analyse de Fourier permet de résoudre la question des cordes vibrantes en décrivant à chaque instant la forme que prend la corde comme une somme d’harmoniques en cours d’amortissement. Cela illustre l’idée visionnaire de considérer tout phénomène physique comme une somme d’oscillations (co)sinusoïdales, entièrement déterminées par les formules de Fourier.

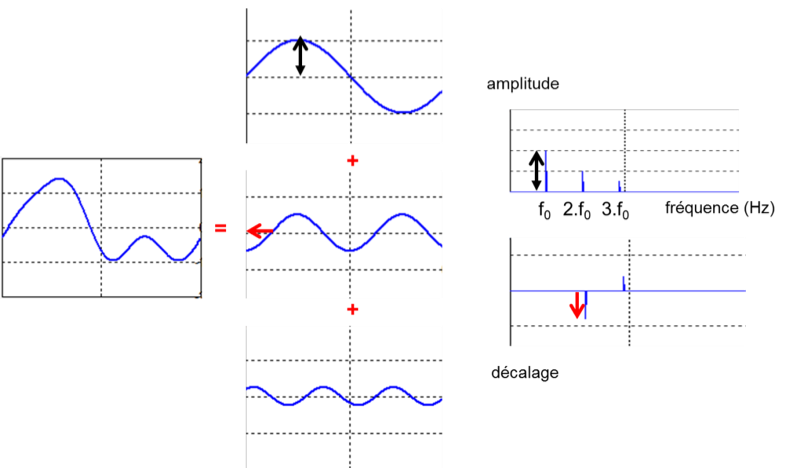
Si un signal possède une période T, c’est-à-dire s’il se répète toutes les T secondes, il se décompose en une somme d’un rythme fondamental (fréquence f₀=1/T ; unité : un Hertz correspond à une répétition par seconde) et de rythmes multiples de celui-ci, dits harmoniques, vocable qui résonne tel l’harmonie des sphères de Pythagore. Sur la figure ci-dessous, le signal de gauche correspond à la somme de trois oscillations au centre : la fréquence fondamentale f0, les harmoniques 2f0 et 3f0. L’amplitude des vibrations correspondantes est représentée par un diagramme en bâtons en haut à droite, couramment appelé spectre, tandis que le décalage, usuellement appelé déphasage et correspondant intuitivement à un retard angulaire pour un objet en rotation, est représenté en bas, généralement évalué en degrés.

Or, quel domaine nous apparaît naturellement peuplé de cycles si ce n’est le mouvement des astres qui a de tout temps inspiré les savants ? Le mathématicien perse Al-Tusi avait prouvé qu’une composition de deux mouvements circulaires pouvait aboutir à un mouvement rectiligne. Cela peut être vu comme un cas particulièrement simple de somme d’oscillations à même d’illustrer la puissance descriptive de ce type de procédé. Si un signal n’est pas périodique, toutes les fréquences peuvent être présentes et l’on utilise une transformée de Fourier en lieu et place des séries du même nom. Les astronomes ont toujours été pionniers dans l’utilisation des outils de Fourier, que cela soit pour la spectroscopie à transformée de Fourier afin d’étudier l’atmosphère des planètes ou encore pour obtenir de bonnes images en combinant plusieurs instruments d’observation. D’ailleurs, les premières innovations dans ce dernier domaine proviennent des astronomes australiens dont les principes sont à l’origine de techniques indispensables en télécoms comme l’ADSL, le WiFi ou autre 4G.

Concrètement, la représentation donnée sur la figure précédente est fournie par un analyseur harmonique ou analyseur de spectre. Il y eut une grande diversité de techniques plus ou moins astucieuses pour réaliser ce type d’appareil. Citons par exemple le prédicteur de marées de Lord Kelvin, purement mécanique, ou encore l’analyseur harmonique à flammes d’Helmholtz tel que figuré ci-dessous (à gauche), utilisant des résonateurs reliés à des capsules de gaz (en-dessous) elles-mêmes reliées à un brûleur. Sur la gravure (à droite), se trouve représentée l’agitation des flammes apparaissant sur le miroir tournant visible sur la photo à gauche, permettant d’identifier les composantes « musicales » de la voyelle « o »

À gauche : analyseur de sons de Rudolph Koenig. Crédit photo : Musée des sciences et de la technologie du Canada
Au milieu : Gravure ancienne représentant des flammes produites par une capsule manométrique de Koenig et stabilisées par effet stroboscopique au moyen d’un miroir tournant. La hauteur de la flamme représente l’intensité du son. Source : Les amis du musée historique du lycée Hoche
À droite : Résonateur de Helmholtz en laiton. Crédit photo : CC BY-SA 2.5, sur Wikimedia Commons

Revenons à la soumission de 1811 à l’Académie des sciences. Que lit-on en bas en droite de la copie du manuscrit ? « et ignem regunt numerii » (« même le feu est régi par les nombres »), une citation que l’on attribue à Platon. Le langage de la nature serait-il le même que celui de la musique ?

À noter que Fourier doit aussi à Platon sa devise « Scientia amica omnibus », c’est-à-dire « La science est la propriété commune de tous les hommes », une devise aussi visionnaire qu’humaniste pour cet orphelin issu de la Révolution Française.

Un héritage universel

Comme le dit si bien le vulgarisateur Ian Stewart, « une équation dit que deux choses différentes sont la même chose ». Le symbole d’égalité, = , représente deux droites parallèles. Les relations mathématiques jettent en quelque sorte des ponts entre des catégories d’objets différents mais dont des études aux cheminements parallèles nous révèlent les analogies. Les symboles qu’elles mettent en œuvre permettent une écriture plus universelle, plus claire et plus rigoureuse que les mots de toute autre langue. Mais, concrètement, ces analogies se sont-elles révélées fertiles ?

D’une manière générale, la notion de flux s’est généralisée à l’ensemble de la physique. C’est lors d’échanges avec Fourier qu’Ampère trouvera l’inspiration sur la circulation du courant électrique. Bien sûr, cela ne s’arrêtera pas à l’électricité et Ohm jettera le pont avec l’acoustique. L’étude de la propagation des sons pour détecter les obstacles rendant la navigation marine périlleuse puis, durant la Première Guerre mondiale, le problème de la localisation des canons ennemis, contiennent les germes qui donneront naissance aux concepts modernes de traitement du signal, domaine où l’Analyse de Fourier est omniprésente. Les progrès de l’électricité permettront alors un traitement automatisé du son. Il est intéressant de noter qu’en France l’Optique dite de Fourier est née des réflexions du physicien Pierre-Michel Duffieux, celui-ci ayant auparavant travaillé sur la propagation de la chaleur à des fins de réfrigération et de transport de viande pour les besoins de ravitaillement dans les tranchées de la Grande Guerre. Ces aspects de l’histoire des sciences et techniques, et bien d’autres encore, sont richement évoqués et illustrés dans l’ouvrage collectif Des cordes aux ondelettes (Presses de l’Université de Provence, 2002). N’oublions pas aussi, en ces temps de réchauffement climatique, que Fourier est également le véritable « père » de l’effet de serre !

Exposition La voix, Cité des sciences et de l’industrie (Paris 2014). Photo By Jean-Pierre Dalbéra [CC BY 2.0], via Wikimedia Commons.

Lire la partition de la nature, une problématique toujours d’actualité

Les outils de Fourier permettent de lire les harmoniques purs contenus dans la « musique de la nature ». Ils sont donc idéalisés : stationnaires, sans début et sans fin. Or, les phénomènes étudiés revêtent souvent un caractère transitoire : ils démarrent puis s’éteignent. Par conséquent, les vibrations sont localisées, comme les notes de musiques dans une partition. Pour réellement commencer à lire la partition de la nature en tant que telle, il faudra attendre la fin du XX^e siècle avec la naissance des ondelettes, dignes descendantes de l’Analyse de Fourier, permettant l’identification de fréquences localisées, concrétisées sur la photo ci-contre de l’expérience observer sa voix (exposition temporaire La Voix, Cité des Sciences, Paris 2014) où l’on lit verticalement les fréquences, avec les notes correspondantes, en fonction du temps qui se déroule horizontalement. Les ondelettes permettent d’analyser aussi bien la voix que les signaux sismiques et même jusqu’aux ondes gravitationnelles, mais c’est l’objet d’un autre article sur Interstices, « Au-delà de Fourier, un monde qui vibre » de Patrick Flandrin.