Calculer dans un monde hyperbolique ?
Selon la géométrie de l’espace où nous calculons, nous pouvons, ou non, faire certains calculs et comme vous le découvrirez bientôt, dans un monde hyperbolique, nous calculons bien mieux que dans notre monde euclidien habituel ! Ce résultat est contraire à ce que nous pensions jusqu’à ces dernières années : la théorie du calcul et des classes de complexité mesurant les difficultés du calcul n’est pas indépendante de la géométrie. En particulier, dans un espace hyperbolique, la conjecture classique P = NP a une réponse positive. Cette réponse ne rapportera pas aux chercheurs qui l’ont démontrée le million de dollars offert par la fondation Clay pour la résolution de cette conjecture, car le prix est réservé à la version euclidienne, toujours ouverte.
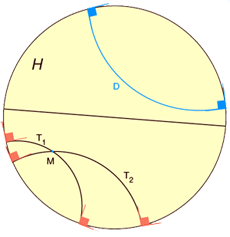
Les points du plan hyperbolique de Poincaré sont à l’intérieur du disque H de rayon 1 et, dans ce plan hyperbolique, les droites sont les diamètres et les arcs de cercles orthogonaux au pourtour du disque. Par un point M extérieur à une droite D ainsi définie, il passe plusieurs droites hyperboliques T1, T2, ne coupant pas la droite D, donc parallèles à D : l’axiome des parallèles de la géométrie euclidienne n’est pas satisfait, mais tous les autres axiomes sont vérifiés par ces points et droites hyperboliques.
Infographie : Pour la Science
Ces nouveaux résultats mathématiques illustrent, là encore, combien le terme « calculer » est délicat à comprendre et que les rapports entre théorie du calcul et monde réel de la physique et de la géométrie ne sont pas tous éclaircis. Il a déjà été établi que la mécanique quantique et la relativité générale avaient des effets sur ce qui est calculable en théorie. Ici, nous examinerons l’effet de la géométrie sur la rapidité des algorithmes.
Les informaticiens, comme les mathématiciens, sont longtemps restés aveugles aux variantes de la géométrie. Pendant des siècles, les mathématiciens ont cherché à démontrer le cinquième postulat d’Euclide également connu sous le nom d’axiome des parallèles : « par un point extérieur à une droite D, il passe une droite unique (nommée parallèle) qui ne coupe pas D ». De nombreuses démonstrations de ce postulat des parallèles ont été proposées à partir d’autres postulats de la géométrie, et, pour chaque tentative, les mathématiciens découvrirent, soit une erreur manifeste, soit qu’une hypothèse équivalente au postulat des parallèles avait été subrepticement utilisée.
Finalement, le mathématicien russe Nikolaï Lobatchevski (1792-1856) et le hongrois Janos Bolyai (1802-1860) découvrent indépendamment (mais après Carl Friedrich Gauss, qui n’avait pas souhaité publier ses découvertes sur le sujet) qu’en supposant qu’aucune parallèle n’existe – géométrie elliptique – ou au contraire que plusieurs parallèles existent – géométrie hyperbolique –, on obtient des univers géométriques intéressants et cohérents. En proposant en 1868 un modèle de la nouvelle géométrie elliptique, le mathématicien italien Eugenio Beltrami (1835-1900) montre que celle-ci ne peut pas conduire à des contradictions, à moins que la géométrie euclidienne ne soit elle-même contradictoire. Examinons le principe de ces raisonnements à propos du modèle proposé par Henri Poincaré.
Quand les droites sont des cercles
Un modèle est une façon de redéfinir ce que l’on appelle « point » et « droite », telle qu’avec les nouveaux points et les nouvelles droites, les axiomes de la géométrie soient satisfaits : par deux points passe une droite et une seule ; deux droites se coupent en un point, etc. Dans le modèle de la géométrie hyperbolique de Poincaré (voir la figure ci-dessus), les points du plan hyperbolique sont les points du disque (dénommé H) de rayon 1 situé dans le plan euclidien. Les droites hyperboliques sont les arcs de cercles orthogonaux au cercle frontière de H, et, en particulier, les diamètres de H. Les axiomes habituels de la géométrie, à l’exception du postulat sur les parallèles remis en cause ici, sont vérifiés avec ces notions redéfinies de points et de droites. Par exemple, deux points distincts de H déterminent une droite hyperbolique unique car, par deux points, il passe un cercle et un seul orthogonal au cercle frontière.
Tout théorème de géométrie démontré sans utiliser l’axiome des parallèles est vrai dans le plan de Poincaré. En revanche, l’axiome des parallèles n’y est pas vrai car, par un point donné, passent une infinité de droites hyperboliques ne coupant pas une droite hyperbolique donnée. Si une contradiction provenait des axiomes habituels auxquels on ajoute l’axiome qu’il y a plusieurs parallèles à une droite donnée passant par un point donné, cette contradiction deviendrait une contradiction de la géométrie des arcs de cercles dans le plan euclidien. Donc s’il n’y a pas de contradiction dans la géométrie euclidienne habituelle, il ne peut pas y en avoir non plus dans la géométrie hyperbolique, que l’on doit considérer avec autant de sérieux que la géométrie euclidienne.
Attention aux distances
Une des propriétés du plan hyperbolique est trompeuse : en effet, les distances n’y sont pas conservées. Plus on s’approche du bord, plus les points, proches en apparence, sont, en réalité éloignés. Si nous observions des êtres vivants à la surface du plan de Poincaré, nous verrions leur taille diminuer à mesure qu’ils s’approchent du bord du disque, qui pour eux est inaccessible, car infiniment loin. En fait, comme dans le plan euclidien, tous les points du plan hyperbolique H sont équivalents, c’est seulement la représentation que nous nous en faisons dans le plan euclidien qui nous donne l’illusion qu’il y a un centre. Une formule compliquée permet de connaître à quelle distance se situent deux points du plan H, de coordonnées (x, y) et (x’, y’), pour les habitants du plan de Poincaré.
John Lamping et Ramana Rao, du Centre de recherche Xerox (PARC) à Palo Alto, proposent de développer des interfaces informatiques où le disque de Poincaré est utilisé pour se déplacer commodément dans de très grands graphes en exploitant la diminution de l’échelle du plan de Poincaré qui permet d’emmagasiner plus de données dans certaines parties que l’on veut examiner en détail.
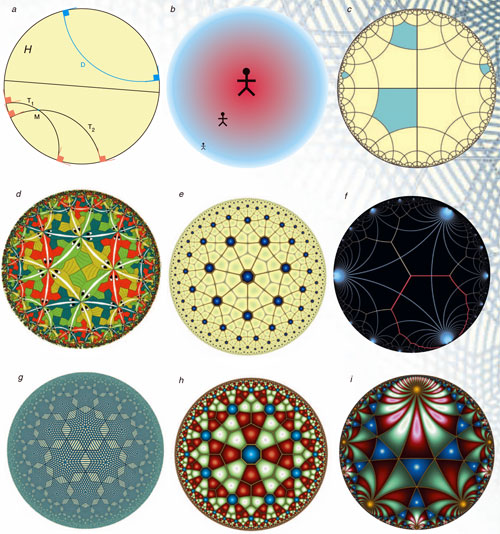
Tout se passe comme si le disque était un monde physique où le coefficient de dilatation variait fortement en fonction de la température, laquelle diminuait du centre vers la périphérie, comme la taille apparente des objets (b). Dans le plan hyperbolique, on peut construire ainsi des pentagones n’ayant que des angles droits (c). Les éléments d’un pavage hyperbolique rétrécissent quand on s’éloigne du centre, comme l’a représenté l’artiste hollandais Escher (d) ; le pavage (e) est obtenu par la juxtaposition de triangles « équilatéraux » d’angle 2π / 7, ce qui permet d’en regrouper 7 autour d’un même point et de paver ainsi tout le plan hyperbolique.
Remarquons que, dans une telle figure, tous les triangles ont la même taille et aucun n’est plus au centre que les autres ; c’est seulement la représentation que nous nous en donnons à l’aide du plan de Poincaré qui produit des triangles différents. La figure (e), œuvre de l’artiste Jos Leys, associe le pavage avec les triangles d’angle 2π / 7 et son pavage dénommé dual (où l’on relie les centres des triangles), ce qui donne un pavage du plan hyperbolique par des heptagones réguliers. La figure (f) représente un pavage par des polygones à un nombre infini de sommets, des « infinigones », dont les angles sont tous ici de 120 degrés. Les figures (g), (h), (i), sont aussi des créations de Jos Leys en géométrie hyperbolique.
Si le plan de Poincaré ne respecte pas les distances du plan euclidien — s’ils sont près du cercle limite, deux points peuvent sembler proches alors qu’en réalité, ils sont très éloignés —, il conserve néanmoins les angles du plan euclidien normal : deux droites hyperboliques (c’est-à-dire deux arcs de cercles) qui se croisent et dont les tangentes en leur point d’intersection font des angles de 60 degrés correspondent pour les êtres du plan hyperbolique à deux droites faisant des angles de 60 degrés et il en va de même pour tout autre angle.
Des étrangetés hyperboliques

L’art du crochet au service du plan hyperbolique. La longueur du périmètre d’un cercle du plan de Poincaré augmente exponentiellement en fonction du rayon. C’est pourquoi, quand on réalise dans notre espace des surfaces correspondant au plan hyperbolique [en respectant les angles et les distances de notre espace euclidien], ces surfaces se replient dans tous les sens, sans qu’il soit possible de les mettre à plat.
Créé et réalisé au crochet par Daina Taimina. D. W. Henderson, Experiencing Geometry (Prentice-Hall, 2001)
Pour mieux comprendre la géométrie hyperbolique, on peut concevoir des bouts de surface de notre espace euclidien à trois dimensions qui donnent une autre vision de ce qu’est le plan hyperbolique en respectant cette fois les angles et les distances. Des mathématiciens ont réalisé, avec du fil et en utilisant la technique du crochet, des morceaux de surfaces qu’il est impossible d’aplatir (car ceux-ci se gaufrent lorsqu’on tente de les faire coïncider avec un plan) et qui correspondent exactement à une partie du plan hyperbolique. Si l’on prend un bout de la surface d’une sphère découpé dans un ballon de cuir, on sait d’avance qu’il est impossible d’aplatir ce morceau qui est bombé et se déchirera si on essaye : il faudrait que la surface accepte de se distendre et cela d’autant plus qu’on est loin du point central que l’on plaque contre le plan. Il n’est pas possible d’aplatir les surfaces correspondant au plan hyperbolique pour une raison inverse : à une distance donnée d’un point, il y a cette fois trop de surface ; pour aplatir un bout de plan hyperbolique, il faudrait que la matière se contracte et cela d’autant plus qu’on est loin du point central. Cet excès de surface est exploité par le calcul hyperbolique : il permet de placer un grand nombre d’unités de calcul à courte distance.
La géométrie hyperbolique présente des étrangetés qui ont pour conséquence des propriétés calculatoires particulières :
D’abord, la somme des angles d’un triangle est toujours inférieure à 180 degrés (c’est-à-dire π radians). La différence entre π et cette somme est d’ailleurs une mesure de l’aire du triangle. Une conséquence de cette propriété est que la surface d’un triangle ne peut dépasser π : les triangles peuvent avoir une grande taille, mais pas une grande surface.
Ensuite, il n’existe pas de rectangle – quadrilatère ayant 4 angles droits – dans le plan hyperbolique. En effet, la somme des angles d’un quadrilatère hyperbolique est toujours strictement inférieure à 2π radians. Les « carrés » sont alors des quadrilatères ayant quatre côtés de même longueur a et quatre angles égaux à un certain angle α inférieur à π / 2, α dépendant de a.
Il existe également toutes sortes de polygones réguliers inattendus dont en particulier un pentagone régulier – le pentagone régulier droit – dont les angles sont tous égaux à π / 2 : ce polygone joue un rôle important dans le calcul en plan hyperbolique. Il existe aussi un hexagone régulier droit et, pour tout n supérieur à 4, un polygone régulier à n côtés dont les angles valent tous π / 2.
En disposant correctement une suite infinie de polygones réguliers à partir d’un même point, on obtient une figure limite qu’on nomme un infinigone. Il s’agit d’une sorte de polygone ayant une infinité de côtés de longueurs égales et faisant entre eux des angles égaux. Son rôle, dans certaines méthodes de calcul hyperbolique, est lié à son étrange propriété d’avoir une infinité de voisins identiques, qui eux-mêmes en ont une infinité, le tout permettant d’organiser des réseaux surpuissants.

La figure ci-dessus représente un pavage par des polygones à un nombre infini de sommets. Ces polygones, également appelés des « infinigones » (en rouge), ont tous ici des angles de 120 degrés.
Infographie : Pour la Science
Le problème de la quadrature du cercle admet une solution positive (résultat de N. Nestorovich et W. Jagy) : dans le plan hyperbolique, il est en effet possible de construire à la règle et au compas un cercle et un carré (quatre côtés égaux et quatre angles égaux non droits) ayant la même aire. Cependant, une telle construction n’est réalisable que pour des cercles bien particuliers et soigneusement caractérisés. Connue depuis plus de 50 ans, cette propriété du plan hyperbolique aurait dû attirer l’attention des mathématiciens, car faire des tracés à la règle et au compas est une sorte de calcul géométrique. La possibilité de quarrer le cercle — c’est-à-dire de réduire le cercle en un carré — sur le plan hyperbolique suggérait donc des caractéristiques spéciales propices à l’organisation de calculs inhabituels.
Des triangles d’angles au sommet π / p, π / q, π / r peuvent paver le plan si (1 / p) + (1 / q) + (1 / r) < 1 (théorème de Poincaré) et une multitude de pavages par des polygones réguliers du plan sont possibles, ce qui est bien plus riche que le plan euclidien qu’on ne peut paver qu’avec des triangles équilatéraux, des carrés et des hexagones réguliers. Assez étrangement, en dimension supérieure, les choses sont moins favorables à la géométrie hyperbolique : alors que l’espace euclidien de dimension n peut toujours être pavé par des polyèdres réguliers (des cubes de dimension n), l’espace hyperbolique, lorsque n dépasse 5, ne peut plus être pavé par aucun polyèdre régulier.
De la géométrie au calcul : la complexité
Les propriétés du plan hyperbolique et particulièrement l’existence d’un pavage régulier par des pentagones droits sont au cœur de l’analyse des possibilités computationnelles de cette géométrie et établissent sa supériorité sur la géométrie euclidienne. Signalons en passant que la géométrie elliptique est sans intérêt pour le calcul, car l’espace total y est fini et ne laisse la place qu’à des calculs par avance bornés.
Trier les n nombres d’une liste désordonnée demande un temps proportionnel à n2 en utilisant la méthode la plus simple : on prend les nombres un à un, puis on construit une nouvelle liste obtenue en insérant au bon endroit chaque nombre de l’ancienne liste dans la nouvelle. Le tri est un problème dont le temps d’exécution est majoré par un polynôme du nombre des données, donc est faisable en pratique : en informatique, on n’a aucun mal à trier de très longues listes. Ces problèmes polynomiaux constituent la classe de complexité P.
La classe NP est celle des problèmes qu’on ne sait pas toujours résoudre en temps polynomial, mais dont on sait vérifier les solutions en temps polynomial quand elles sont connues. Par exemple, factoriser un nombre composé, n, en deux facteurs tels que n = pq, avec p et q différents de 1, est aujourd’hui considéré comme non polynomial (personne ne sait le résoudre en temps polynomial et l’on conjecture que ce n’est pas possible). En revanche, vérifier que p x q donne bien n quand p et q sont donnés ne demande qu’un temps polynomial (fonction de la longueur de p et q), car cela ne nécessite qu’une multiplication, ce qui est facile et rapide. Les problèmes dont on sait contrôler les solutions en temps polynomial constituent la classe NP. Le problème de la factorisation est donc dans NP et probablement pas dans P.
Le prix d’un million de dollars est offert à qui saura établir que P et NP sont différents ou — ce qui étonnerait tout le monde — que P est identique à NP. Pour gagner ce prix, une méthode consisterait à proposer une démonstration que la factorisation d’un entier ne peut, en général, pas être menée en temps polynomial par un algorithme déterministe.
Depuis que nous savons faire coopérer plusieurs processeurs pour former des réseaux d’ordinateurs, la notion de problème polynomial a été réexaminée, et lors de ce réexamen, la différence entre le plan euclidien et le plan hyperbolique est apparue. Lorsqu’un nombre fixé k d’unités de calcul travaillent ensemble, le temps de calcul est au mieux divisé par k (souvent beaucoup moins), et donc ce qui était polynomial avec une unité de calcul, le reste avec k unités de calcul.
Espace de calculateurs : interconnecter des processeurs dans un espace euclidien
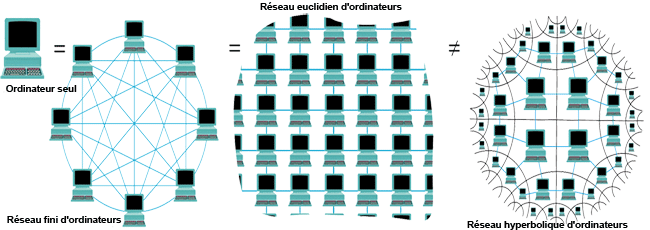
Le parallélisme euclidien et hyperbolique. Un problème dépendant des données d est dans la classe de complexité P si on peut traiter les données d en un temps de calcul majoré par un polynôme dépendant de la taille des données t (par exemple 5t3). Le calcul du produit de deux nombres entiers est dans la classe P. Dans cette définition, il est sous-entendu qu’on n’utilise qu’une seule unité de calcul, mais si on s’autorise à en utiliser k (un nombre entier), cela ne change pas la définition. De même, on ne change pas la définition de la classe P si on s’autorise à utiliser une infinité d’unités de calcul réparties régulièrement dans un espace euclidien et communiquant entre elles avec une vitesse limitée (par exemple, la vitesse de la lumière). Le calcul parallèle ou en réseau (même illimité), dans un espace euclidien, ne change pas la classe P des problèmes traitables en temps polynomial. En revanche, si on considère des réseaux d’unités de calcul dans un espace hyperbolique, la classe des problèmes traitables en temps polynomial change. On note P’ la nouvelle classe. Certains problèmes (dont la factorisation des entiers) dont on ne pense pas qu’ils sont dans P sont pourtant dans la classe P’. Le parallélisme des calculs dans l’espace hyperbolique change la notion de problème polynomial. Dans un espace hyperbolique (et avec une infinité d’ordinateurs), casser les codes de cartes de crédit serait un jeu d’enfant.
Infographie : Pour la Science
Si nous imaginons que le plan ou l’espace est partout occupé par des unités de calcul, la question de savoir ce qui est polynomial prend un nouveau sens. Pour un problème donné, par exemple la factorisation, la question devient : pouvons-nous concevoir un réseau de calculateurs (éventuellement illimité) qui traite en temps polynomial tout cas particulier du problème en répartissant le travail sur autant d’unités de calculs que nécessaire ? Si la réponse est oui, nous dirons que le problème est parallèlement polynomial, sinon qu’il ne l’est pas. Comme l’ont remarqué Dara Morgenstein et Vladik Kreinovich en 1995, c’est là qu’intervient la géométrie de l’espace et que le plan de Poincaré surpasse le plan euclidien.
Dans un espace euclidien de dimension d, le volume d’une sphère de rayon r est proportionnel à rd. La vitesse de communication entre les unités de calcul est bornée par la vitesse c de la lumière et les unités de calcul occupent chacune un espace minimal fixé (une concentration infinie d’unités de calcul est impossible) : dans une durée de temps polynomiale t(n), le nombre d’unités de calcul qui peuvent participer au calcul est au plus proportionnel à t(n)d, ce qui est encore polynomial. Il en résulte que dans un espace euclidien, le fait d’envisager des calculs parallèles même sur un réseau infini d’unités de calcul, ne change pas la classe des problèmes traitables en temps polynomial. Certes, on pourra aller plus vite, mais le gain de rapidité ne transformera jamais un problème non polynomial en problème polynomial. Dans le plan euclidien, tout problème parallèlement polynomial est polynomial, et inversement.
Dans un plan et un espace hyperboliques, il en va tout autrement. En effet, le volume d’une sphère y croît exponentiellement en fonction du rayon de la sphère (c’est ce que suggère la réalisation du plan hyperbolique en fil crocheté), et donc il est possible de faire participer un nombre exponentiellement croissant d’unités de calcul à la résolution d’un seul problème. En particulier, tout problème de la classe NP, en s’y prenant bien, devient traitable en temps polynomial. Si P’ est la classe des algorithmes qu’on peut traiter en temps parallèlement polynomial dans un plan hyperbolique, P’ est plus grand que NP.
Depuis 1995, bien des choses ont été précisées et tout un nouveau domaine d’informatique géométrique s’est développé. Grâce aux travaux de Maurice Margenstern, de l’Université de Metz, et des collègues français, japonais et allemands qu’il a entraînés dans son aventure, nous savons maîtriser le parallélisme hyperbolique. D’abord, Maurice Margenstern a adapté au plan hyperbolique la notion de réseau d’automates cellulaires. Charles Babbage, au milieu du XIXe siècle, avait dessiné avec une parfaite précision des ordinateurs mécaniques qu’il ne construisit jamais à cause des difficultés techniques considérables qu’il aurait fallu surmonter. De la même façon, M. Margenstern, sans bien sûr pouvoir mettre en œuvre ses réseaux cellulaires hyperboliques, les a définis et programmés avec une précision minutieuse. Grâce à lui, non seulement la connaissance des pavages réguliers du plan et de l’espace hyperbolique a progressé ainsi que la compréhension du calcul parallèle hyperbolique, mais ce qu’il a défini nous permettrait de profiter de ces espaces si nous nous y trouvions projetés. Mathématiques et informatique théorique deviennent de merveilleuses sciences oniriques !
À l’attaque du problème logique de la satisfiabilité
Le problème de la satisfiabilité a d’abord retenu l’attention. Ce problème consiste à résoudre un système d’affirmations logiques du type {non b, a ou b ; non a ou c ou d ; b ou non c} c’est-à-dire à trouver si les inconnues a, b, c… sont vraies ou fausses (si a est vraie, non a est fausse et inversement). Dans cet exemple, on déduit des affirmations que b est faux (car non b est alors vraie), que a et d sont vrais et que c est faux, donc la solution est {a, non b, non c, d}. La satisfiabilité est un problème NP-complet : si nous savions le résoudre en temps polynomial, nous pourrions résoudre tous les problèmes NP en temps polynomial : on connaît en effet des méthodes transformant tout problème NP en problème de satisfiabilité. Or M. Margenstern et Kenichi Morita, de l’Université d’Hiroshima, ont conçu en 2001 un procédé de résolution du problème de la satisfiabilité en temps polynomial fondé sur l’utilisation d’un pavage du plan hyperbolique par des pentagones réguliers droits, chacun portant une unité de calcul élémentaire à mémoire finie ne communiquant qu’avec ses voisins immédiats et fonctionnant à partir du même jeu d’instructions (c’est précisément ce que l’on nomme un réseau d’automates cellulaires).
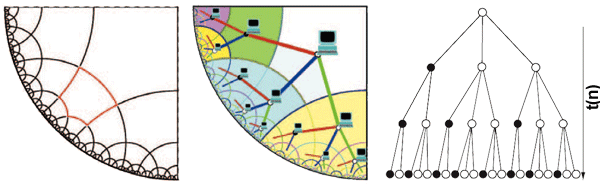
Pour résoudre en temps polynomial le problème de la satisfiabilité (qui est un problème NP-complet, et qu’on ne sait résoudre qu’en temps exponentiel dans le plan euclidien même en disposant d’ordinateurs parallèles), Maurice Margenstern et Kenichi Morita proposent d’utiliser un pavage du quart de plan hyperbolique par des pentagones droits (comme le pentagone en rouge). Ces pentagones portent chacun un petit calculateur qui communique avec ses voisins.
Infographie : Pour la Science
L’organisation du calcul sur le réseau ci-dessus — il s’agit d’un réseau d’automates cellulaires — s’opère en faisant communiquer les processeurs de manière à ce qu’ils constituent un arbre. Cet arbre, appelé arbre de Fibonacci, contient deux types de nœuds : les nœuds blancs ayant trois fils et les nœuds noirs ayant deux fils. À la racine, il y a 1 nœud blanc ; à la profondeur 1, il y a 1 nœud noir et 2 nœuds blancs ; au niveau suivant, il y a 3 nœuds noirs et 5 nœuds blancs ; au niveau suivant, il y a 8 nœuds noirs et 13 nœuds blancs. On reconnaît la suite de Fibonacci 1, 1, 2, 3, 5, 8, 13 où chaque terme est la somme des deux précédents. La croissance de cette suite est exponentielle (du type C Φn où Φ est le nombre d’or), ce qui est très important ici. En effet, cela signifie que le nombre d’automates auxquels on accède à partir de la racine en t secondes en suivant les arcs de l’arbre augmente exponentiellement en fonction de t. C’est la clé de la méthode de résolution en temps polynomial du problème de la satisfiabilité par un réseau d’automates cellulaires sur le plan hyperbolique.
Cette implémentation exploite la possibilité de connecter les cases du réseau pentagonal droit pour qu’elles forment un arbre infini dont le nombre de nœuds augmente exponentiellement en fonction de la profondeur. La forme de l’arbre, assez étrangement, fait intervenir la suite de Fibonacci Φ(0) = 1, Φ(1) = 1, Φ(2) = Φ(1) + Φ(0),…, Φ(n + 2) = Φ(n + 1) + Φ(n). Lorsqu’un problème est posé, il est distribué sur les cases pentagonales qui travaillent chacune à traiter une partie du problème, le tout aboutissant à la solution en un temps de calcul polynomial, car un nombre exponentiel de calculateurs du réseau participent à sa résolution.
Cette façon particulièrement astucieuse d’utiliser la propriété de la croissance rapide de l’aire d’un disque en fonction de son rayon se généralise à d’autres pavages du plan hyperbolique et de l’espace hyperbolique à trois dimensions. Ceci a pour conséquence que si nous découvrions que notre espace est hyperbolique, nous serions prêts pour y programmer des systèmes résolvant en temps polynomial tous les problèmes NP qu’on ne pourra donc plus alors considérer comme difficiles.
D’autres résultats étonnants ont été obtenus, notamment la conception d’un réseau d’automates du plan hyperbolique possédant la propriété d’universalité, c’est-à-dire ayant la capacité de simuler toute fonction calculable. On savait déjà construire de tels réseaux sur le plan euclidien, mais jamais on n’avait établi ce résultat pour le plan hyperbolique (résultat obtenu en 2001 par F. Herrmann et M. Margenstern). En 2002, C. Iwamoto, M. Margenstern, K. Morita et T. Worsch ont obtenu la caractérisation précise de la classe P’ des problèmes parallèlement polynomiaux du plan hyperbolique comme étant exactement égale à la classe PSPACE des problèmes demandant un espace mémoire polynomial, pour être résolu. Par ailleurs, un modèle de calcul nouveau fondé sur les infinigones permet de résoudre dans le plan hyperbolique des problèmes indécidables. Ce résultat de S. Grigorieff et M. Margenstern montre à nouveau que le plan hyperbolique possède une capacité théorique de calcul singulière.
Plus nous avançons, plus la subtilité du monde du calcul se dévoile et nous surprend. Non seulement l’informatique bouleverse la vie quotidienne de chacun de nous, mais elle sollicite obstinément les mathématiciens en leur posant de nouvelles questions, dont les réponses ne cessent de nous étonner. Les mondes hyperboliques sont finalement bien plus intéressants qu’on ne l’imaginait. Notons toutefois que si notre univers est hyperbolique (ce qui n’est pas exclu par la physique), l’exploitation des nouveaux résultats ne pourra se faire qu’en disposant de réseaux de calculateurs incroyablement grands, tissés dans la galaxie toute entière. Cela réserve les applications éventuelles de cette partie de l’informatique à nos descendants… dans plusieurs siècles au mieux !
Sur le calcul hyperbolique (uniquement en anglais)
- C. Iwamoto et M. Margenstern, A Survey on the Complexity Classes in Hyperbolic Cellular Automata, Multiconference on SCI, Orlando, pp. 31-36, 2003.
- S. Grigorieff, et M. Margenstern, Cellular Automata on Infinigonal Grids of the Hyperbolic Plane, Proceeding of SCI’2002, Orlando, pp. 14-18, 2002.
- M. Margenstern et K. Morita, NP problems are Tractable in the Space of Cellular Automata in the Hyperbolic Plane, in Theoretical Computer Science, n°259, 1/2, pp. 99-128, 2001.
- D. Henderson et D. Taimina, Crocheting the Hyperbolic Plane, Math. Intelligencer, vol. 23, n° 2, pp. 17-27, 2001.
- D. Morgenstein et V. Kreinovich, Which Algorithms are Feasible and Which are not Depends on the Geometry of Space-time, in Geombinatorics, vol. 4, n° 3, pp. 80-97, 1996.
- W. Jagy, Squaring Circles in the Hyperbolic Plane, in Math. Intelligencer, n° 2, pp. 31-40, 1995.
- Bernie Freidin, Hyperbolic and Spherical Tiling Gallery
- Don Hatch, Hyperbolic Planar Tesselations
- Jos Leys, Hyperbolic Tilings
Sur la barrière de Turing (en français et en anglais)
- J-P. Delahaye, Complexités : aux limites des mathématiques et de l’informatique, Éditions Belin Pour la science, chap. 17 : La barrière de Turing, 2006.
- C. Calude et B. Pavlov, Coins Quantum Measurements, and Turing’s Barrier, in Quantum Information Processing, vol.&nsp;1, n° 1-2, pp. 107-127, 2002.
- G. Etesi et I. Németi, Non-Turing Computations via Malament-Hogarth Space-times, in International Journal of Theoretical Physics, vol. 41, n° 2, pp. 341-370, 2002.
Une première version de ce document est parue dans la rubrique « Logique et calcul » de la revue Pour la Science, n°316, en février 2004. Le texte de cet article constitue le chapitre 19 du livre de Jean-Paul Delahaye, « Complexités : aux limites des mathématiques et de l’informatique. », publié aux Éditions Belin Pour la science (2006).
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Jean-Paul Delahaye
Professeur émérite d'informatique à l'Université des Sciences et Technologies de Lille (Lille 1) et chercheur au Centre de recherche en informatique, signal et automatique de Lille (CRIStAL).