Construire des logiciels fiables
Les « bugs » informatiques, c’est-à-dire les erreurs involontaires de programmation, peuvent avoir des conséquences désastreuses, quand elles ont lieu dans un logiciel critique, comme dans un centre d’appel téléphonique d’urgence (cf. la panne des numéros d’urgence en France en juin 2021), ou pire dans le système de sécurité d’une centrale nucléaire. Nous allons voir comment la programmation défensive formellement vérifiée, en complément des méthodes traditionnelles du génie logiciel, permet de réduire significativement les risques de telles erreurs. En passant, nous discuterons de pensée floue, puis de formalisation mathématique en l’illustrant sur des problèmes proches des « sudokus » (en fait les problèmes SAT booléens).
À première vue, les erreurs involontaires de programmation logicielle, plus ordinairement appelées « bugs », ont des causes multiples : erreurs d’étourderie ou d’inattention (par exemple, interversion des noms « i » et « j ») ; contresens sur la signification d’un morceau de programme ou du cahier des charges (censé donné la description du comportement attendu du logiciel) ; sur-interprétation d’un cahier des charges ambigu, incomplet ou contenant du non-dit ; vraie erreur de raisonnement (par exemple mauvaise compréhension d’un concept, utilisation d’une hypothèse implicite fausse) ; etc. Pour empêcher ou détecter de telles erreurs lors du développement logiciel, l’état de l’art recommande de combiner un ensemble de « bonnes pratiques ». En pratique, il reste cependant toujours des bugs qui sont détectés bien trop tard, une fois que le logiciel est déjà entré en service.
À titre d’exemples, citons :
- « bonnes » abstractions au cœur des langages de programmation (variables, fonctions, types, structures de contrôle, etc.) ;
- patrons de conception (modèle-vue-contrôleur en programmation web, itérateurs pour les parcours de structures de données, etc.) ;
- vérifications statiques (typage) ;
- vérifications dynamiques (programmation défensive, tests) ;
- pratiques et outils organisationnels (par exemple gestion de version, intégration continue, revue de code, literate programming, méthodes agiles, etc.).
Erreurs et pensée floue
Les sciences cognitives apportent un éclairage sur cette difficulté à construire des logiciels sans bug. Par exemple, considérons le problème suivant :
« Une balle et une batte coûtent au total \(1,10\) $. La batte coûte \(1\) $ de plus que la balle. Combien coûte la balle ? »
Selon le psychologue et économiste américano-israélien Daniel Kahneman, prix Nobel d’économie en 2002 pour ses travaux sur les biais cognitifs, la plupart d’entre nous (d’après les résultats de sondages réalisés sur les campus américains) répondent incorrectement « la balle coûte \(10\) cents », surtout si la réponse doit être donnée rapidement sans avoir le temps de réfléchir. Autrement dit, nous calculons intuitivement \(1,10 − 1 = 0,10\) sans nous rendre compte que le prix de la batte serait alors lui-même de \(1,10\) $ et donc que le coût total serait de \(1,20\) $. Le calcul correct est en fait légèrement plus compliqué : \(10\) cents, c’est ce qui reste à payer quand on a donné le dollar supplémentaire pour la batte, il reste à partager ce prix équitablement entre la balle et la batte. Le calcul correct est donc \((1,10 − 1) ÷ 2.\)
L’origine de telles erreurs s’explique par le fait que nous pensons principalement et préférentiellement de façon « floue ». Par exemple, considérons le concept familier de canard. Scientifiquement, ce concept n’est pas un taxon bien défini de la classification systématique des espèces vivantes : il est considéré comme ambigu. L’intérêt de ce concept flou, c’est que tout en s’appliquant à un grand nombre d’individus différents, il nous permet de distinguer instantanément et sans effort un canard d’un lapin, ce qui s’avère par exemple très utile pour anticiper les mouvements possibles de l’animal. Mais, comme le montre le dessin ci-dessous, ce flou est déformable jusqu’à l’absurde. Un tel flou entoure en fait la plupart de nos concepts (un autre exemple : combien de cheveux doit porter une tête pour cesser d’être « chauve » ?), et plus généralement de nos pensées, même verbalisées.

Artiste inconnu, Public domain, via Wikimedia Commons.
Regardons à nouveau le dessin ci-contre. Parmi les deux phrases entre guillemets suivantes, quelle est celle qui vous semble la plus appropriée pour caractériser ce que vous voyez ?
« je vois une tête de canard ou je vois une tête de lapin »
ou bien « je vois une tête de canard et je vois une tête de lapin » ?
Étonnamment, le « ou » et le « et » semblent ici relativement similaires à quelques nuances près : le « ou » permet de suggérer le caractère non simultané des deux actions « je vois » ; tandis que le « et » permet d’en souligner le caractère contradictoire. Ailleurs, au restaurant par exemple, si le menu propose « fromage ou dessert », il faut choisir entre les deux. Au contraire, chez des proches, une proposition identique en fin de repas n’interdirait pas forcément de prendre les deux. Les mots « ou » et « et » semblent donc s’exclure ou pas en fonction du contexte. Pour éviter cette ambiguïté, les mathématiciens et mathématiciennes en restreignent l’usage en leur donnant un sens très précis. Nous allons y revenir.
Mais donner un sens univoque aux mots ne suffit pas à rendre les phrases non ambiguës. Par exemple, dans la phrase « le tribunal juge l’enfant sauvage », qui juge que l’enfant est sauvage ? Soit c’est le tribunal, si l’adjectif « sauvage » est considéré comme un complément du verbe « juge ». Soit c’est le locuteur ou la locutrice, si cet adjectif est considéré comme un complément du nom « enfant ». Bien sûr une telle ambiguïté grammaticale est évitable : il suffit ici de mettre la phrase sous la forme passive. La difficulté, c’est qu’au moment où nous énonçons ce genre de phrase, nous ne nous apercevons pas forcément de l’ambiguïté qu’elle recèle.
Essayer de penser moins flou est donc long et difficile : il faut beaucoup d’efforts, de la concentration, mais surtout de la méthode dirait Descartes. Car comme illustré ci-dessus, la pensée floue se niche au cœur même des langues humaines. En réaction, depuis plusieurs milliers d’années, les êtres humains construisent un langage dédié à la définition de concepts non flous et à la vérification que les raisonnements sur ces concepts sont corrects. Ce langage, c’est la mathématique.
Contrôler la pensée floue par la formalisation mathématique
La mathématique ne fait pas magiquement disparaître les difficultés, mais elle offre des outils. Notamment, le processus de vérification de la formalisation, qui, « idéalement » (cette vision un peu simpliste sera nuancée par la suite), ne suppose justement plus aucune forme de pensée et peut ainsi être complètement mécanisé. Cela n’interdit pas toute forme d’erreur, notamment des erreurs d’inattention. Mais ce risque est évitable en délégant cette vérification à un programme informatique, pour peu que celui-ci ait été lui-même bien vérifié.

Ainsi, la vérification du raisonnement mathématique est un processus mécanisable, exactement comme la vérification lexicographique — qui vérifie que nos textes n’utilisent que des mots du dictionnaire — ou comme la vérification de la cohérence des unités, méthode apprise au lycée pour vérifier ses solutions aux exercices de physique/chimie. Les langages de programmation s’étant déjà inspirés de tels procédés pour détecter certaines erreurs dans les programmes, via la « vérification des types », une façon de détecter plus d’erreurs de programmation est d’étendre la vérification des types à la vérification des raisonnements justifiant la correction de ces programmes informatiques. Dans les langages de programmation, la « vérification statique des types » généralise la vérification de la cohérence des unités physiques. D’un certain de point de vue, appelé isomorphisme de Curry-Howard, la vérification des preuves mathématiques s’apparente aussi à de la vérification des types.
Heuristique versus vérification
Au contraire du processus de vérification, le processus de formalisation lui-même est extrêmement difficile : c’est là que réside l’art mathématique (pour découvrir comment pense un mathématicien, lire le magnifique « Mathematica » de David Bessis). Aussi, généralement, les mathématiciens et mathématiciennes ne cherchent pas à formaliser comment ils ou elles inventent des mathématiques. Ils se contentent simplement de formaliser pourquoi leurs énoncés sont corrects.
Tout un chacun peut appréhender cette dichotomie entre heuristique et vérification sur des casse-têtes comme les sudokus : il est beaucoup plus rapide et facile de vérifier qu’un candidat de solution à un tel problème est correct, plutôt que d’inventer cette solution.
Vérifier une solution aux \(n\)-reines
Illustrons cela sur les casse-têtes, un peu plus simples, de \(n\)-reines. Dans la version « de base », il s’agit de placer \(n\) reines sur un échiquier de taille \(n × n\) de façon qu’aucune d’elles ne puisse en prendre une autre avec un seul mouvement (pour un mouvement d’une reine aux échecs : vertical, horizontal, ou diagonal). Trouver une solution pour \(n = 4\) demande un peu de réflexion. Mais vérifier que la figure 1 ci-dessus donne une solution est immédiat. Dans une variante, comme sur la figure 2 ci-dessus, l’échiquier peut initialement contenir des cases avec des reines déjà posées, et des cases où il est interdit de poser une reine (mais n’interdisant pas aux reines de « passer » pour en prendre une autre).
À vous d’essayer :
Le problème des \(3\)-reines a-t-il une solution ? Et la variante du problème des \(8\)-reines dessinée sur la figure 2, où une reine est déjà posée en ligne 1 et colonne 1, case notée plus simplement \(11\), et où il est de plus interdit de poser une reine aux cases \(83\) (ligne \(8\), colonne \(3\)) et \(64\) (ligne \(6\), colonne \(4\)) ?
Voilà la réponse pour les \(3\)-reines (il faudra avoir lu le reste de ce document pour pouvoir la déchiffrer) :
−11 ⊖−21 −11 ⊖−22 −11 ⊖ 23 21 22 ⊖−31 −11 ⊖−32 −23 ⊖−33 −23 ⊇ 31 32 33 ;
−13 ⊖−22 −13 ⊖−23 −13 ⊖ 21 22 23 ⊖−31 −21 ⊖−32 −21 ⊖−33 −13 ⊇ 31 32 33 ;
F⊖−11 ⊖−13 ⊖ 12 11 13 ⊖−21 −12 ⊖−22 −12 ⊖−23 −12 ⊇ 21 22 23.
La réponse au problème de la variante des \(8\)-reines est donnée sur la figure 5 ci-dessous.

Figure 5 – Solution au problème des \(8\)-reines avec une reine en \(11\) et les cases \(83\) et \(64\) interdites. C’est l’unique solution.
Preuve visuelle de l’absence d’une solution aux \(n\)-reines
Considérons maintenant le problème des \(4\)-reines avec une reine déjà posée en case \(11\). Ce casse-tête n’a pas de solution. La preuve « visuelle » (voir la figure 3 ci-dessus) permet de le vérifier très simplement. Dans celle-ci, le caractère « ? » représente une case pouvant éventuellement contenir une reine sans être prise ; au contraire, les cases avec un numéro \(k\) sont atteignables par la reine éventuelle de la ligne \(k\). L’absence de solution se déduit de l’impossibilité de placer une reine à la ligne \(4\), celle-ci n’ayant pas de « ? ». Les cases laissées vides peuvent être ignorées dans la preuve d’absence de solution.
Preuve verbalisée de l’absence d’une solution aux \(n\)-reines
Pour expliciter davantage le raisonnement, rédigeons maintenant cette preuve dans un style mathématique plus classique. Utilisons une preuve par l’absurde : en supposant l’existence d’une solution satisfaisant les contraintes, on déduit une contradiction. Cela garantit qu’une telle solution est impossible.
Théorème Il n’y a pas de solution au problème des \(4\)-reines avec une reine en case \(11\).
Preuve
Supposons qu’une telle solution existe.
- Montrons d’abord que la case \(32\) (ligne \(3\), colonne \(2\)) contient une reine : en effet, comme \(21\) et \(22\) sont atteignables depuis \(11\), la reine de la ligne \(2\) est en \(23\) ou \(24\) et elle peut donc atteindre \(34\) ; comme par ailleurs \(31\) et \(33\) sont atteignables depuis \(11\), la reine de la ligne \(3\) est nécessairement en \(32\).
- Montrons ensuite qu’il est impossible de placer une reine en ligne \(4\) : en effet, \(41\) et \(44\) sont atteignables depuis \(11\) ; de même, \(42\) et \(43\) sont atteignables depuis \(32\).
- Absurde : dans toute solution, il doit y avoir une reine en ligne \(4\).
Remarquons que cette preuve s’arrange pour propager des contraintes ligne à ligne, en réduisant le nombre de possibilités de placer une reine à la ligne suivante. Elle reste ainsi concise, en évitant soigneusement une approche naïve par « essai-échec », énumérant tous les placements possibles.
Une approche par « essai-échec » consiste par exemple à « essayer de placer » une reine par ligne en testant successivement toutes les colonnes, jusqu’à trouver une case de la ligne courante non prenable par les reines déjà placées ; si une telle case existe, une reine y est placée et l’algorithme essaye alors de placer la reine de la ligne suivante ; sinon, les essais de placement sur la ligne courante sont un échec, et ils se poursuivent sur les lignes précédentes.
Ainsi, le premier essai de placement sur la ligne 2 a lieu en colonne 3 et est représenté sur l’échiquier de gauche, où chaque case avec un numéro \(k\) correspond à un test indiquant que la case est prenable par la reine en ligne \(k\). Ce premier essai aboutit donc à un échec en ligne 3. Le deuxième et dernier essai de placement sur la ligne 2, représenté sur l’échiquier de droite, aboutit aussi à un échec en ligne 3, après un unique essai de placement possible en ligne 3, ayant lui abouti à un échec en ligne 4, représenté lui-aussi sur la figure.
 |
 |
Comme les essais de placement en ligne 2 aboutissent à un échec, le problème n’a pas de solution. Au final, cette approche par « essai-échec » teste seize cases (les cases de la ligne 3 sont testées deux fois). Le raisonnement sur la figure 3 revient quant à lui à ne tester qu’une fois chacune des cases des lignes 2 à 4, soit douze cases seulement. Mais, inventer une telle preuve concise, qui réduit au maximum les calculs nécessaires à sa vérification, n’est a priori pas évident.
De façon plus générale, les preuves mathématiques évitent d’avoir à tester un nombre élevé, voire infini de cas. Par exemple, nous allons définir dans la suite du procédé de vérification qu’un problème de \(n\)-reines donné a ou n’a pas de solution. Et nous allons prouver mathématiquement que les réponses données par ce procédé sont correctes. Cette preuve le garantira quel que soit le problème de \(n\)-reines, en particulier, quel que soit le \(n\) (il y en a une infinité possible).
Mécaniser la vérification des mathématiques
Pour vérifier de façon vraiment mécanique (notamment à l’aide d’un logiciel) les raisonnements ou les théories mathématiques, il faut développer une théorie mathématique du langage mathématique : c’est ce qu’on appelle une logique formelle. Cela permet de comprendre de façon non floue ce que doit faire le vérificateur et éventuellement de vérifier que ce vérificateur est correct. Comme formaliser « l’ensemble » du langage mathématique serait trop ambitieux, ce document en illustre la méthode sur un minuscule fragment, appelé logique des propositions conjonctives de booléens, tout juste suffisant pour formaliser les problèmes de \(n\)-reines (et de sudokus). Toutefois, cela donne déjà un bon aperçu de comment formaliser la mathématique.
Cette logique élémentaire est toujours un domaine actif de recherche. Les logiciels de résolution des problèmes formulés dans cette logique sont appelés solveurs-SAT. La compétition SAT désigne chaque année les meilleurs solveurs-SAT : cette émulation a permis à l’algorithmique du domaine de progresser de façon spectaculaire ces trente dernières années. Les solveurs-SAT ont aujourd’hui des performances qui leur permettent d’être utilisés dans de nombreuses applications pratiques (par exemple, résoudre les problèmes de dépendances entre logiciels lors d’une mise à jour ou vérifier la conception de circuits électroniques). Mais du point de vue théorique, il n’est toujours pas connu s’il pourrait exister un solveur-SAT classique donnant toujours une réponse en un temps au plus polynomial en fonction de la taille du problème d’entrée. Cette (méta)question appelée « P = NP ? » est un des fameux 7 problèmes, qualifiés « du millénaire » par l’institut Clay, qui en récompenserait la réponse par un million de dollars.
Propositions et variables logiques
Toute logique formelle repose sur un langage de propositions. Une telle proposition représente un énoncé, qui peut valoir soit « vrai », soit « faux », en fonction de l’interprétation des variables apparaissant dans cet énoncé. Dans le cadre de notre logique, les variables sont simplement des entiers naturels non nuls qui sont eux-mêmes interprétés uniquement comme valant soit vrai, soit faux.
Typiquement, pour définir les problèmes de \(n\)-reines dans notre logique, nous représenterons chaque case de l’échiquier par une variable distincte, avec la convention que sa valeur « vrai » signifie « il y a une reine sur cette case ». Dans le cas des \(4\)-reines, nommons chacune des \(16\) variables directement par l’entier qui représente la position de la case dans l’échiquier : \(11\), \(12\),…, \(14\), \(21\), …
Pour définir mathématiquement le langage des propositions, nous aurons éventuellement besoin de nommer des (noms de) variables. Nous utiliserons alors \(x\), \(x\)1, \(x\)2… Autrement dit, chacun de ces \(x\) représentera un entier qui est lui-même une variable logique. C’est un exemple de ce que nous appelons dans la suite des méta-variables : des noms désignant certains fragments des propositions logiques.
Notre langage est bâti sur une hiérarchie de \(3\) catégories de propositions, incluses les unes dans les autres. Ainsi, une théorie sera représentée par une conjonction (c’est-à-dire un « et logique ») de clauses, ces dernières étant alors considérées comme des axiomes de ladite théorie. Les clauses sont elles-mêmes des propositions plus simples que ces propositions conjonctives. Mais commençons par le commencement…
Littéraux
Au niveau le plus élémentaire, les propositions s’appellent des littéraux et sont uniquement soit de la forme « \(−x\) » dont la valeur de vérité est l’opposée de celle de \(x\), soit de la forme « \(x\) » (de valeur de vérité \(x\)). Par exemple, dans la théorie des \(4\)-reines, le littéral « \(34\) » exprime qu’il y a une reine en case \(34\). Le littéral « \(−34\) » exprime qu’il y n’a pas de reine en case \(34\).
Nous utilisons \(ℓ\), \(ℓ\)1, \(ℓ\)2, … comme méta-variables de littéraux. L’opération involutive « \(−ℓ\) » est alors définie comme retournant le littéral de valeur opposée à \(ℓ\) (en ajoutant/supprimant le symbole « \(−\) » devant la variable).
Clauses
Au niveau intermédiaire, les propositions s’appellent des clauses et sont des ensembles finis de littéraux. Nous écrirons ces ensembles sous la forme de liste de littéraux séparés par des espaces. Par définition, une telle clause vaut vrai si et seulement si au moins un de ses littéraux vaut vrai. La clause vide sera écrite « F » et a pour valeur faux.
Par exemple, dans la théorie des \(4\)-reines, l’énoncé « la ligne \(2\) doit contenir au moins une reine » peut s’écrire comme la clause « \(21\) \(22\) \(23\) \(24\) ». Autrement dit, chaque espace représente un « ou » logique. Autre exemple, l’énoncé « les cases \(21\) et \(43\) ne peuvent pas contenir toutes les deux une reine » peut s’écrire comme la clause « \(−21\) \(−43\) ». Un dernier exemple, l’énoncé « si la case \(11\) contient une reine, alors la \(34\) aussi » s’écrit comme la clause « \(−11\) \(34\) ». En effet, « \(−11\) \(34\) » vaut vrai si et seulement si « \(11\) vaut faux ou \(34\) vaut vrai », ce qui est logiquement équivalent à « si \(11\) vaut vrai alors \(34\) vaut vrai » (énoncé en particulier vrai quand \(11\) vaut faux).
Les méta-variables de clauses sont notées \(c\), \(c\)1, \(c\)2, … Nous noterons aussi « \(c\)1 \(c\)2 » la clause résultant de l’union des deux clauses \(c\)1 et \(c\)2 (formée des littéraux étant dans \(c\)1 ou dans \(c\)2). Pour éviter les ambiguïtés en cas d’absence de parenthèses, nous considérons que l’espace est prioritaire sur tous les autres opérateurs binaires introduits par la suite (mais pas le « moins unaire », précédemment introduit). Lorsque nous souhaiterons commencer le calcul par une opération moins prioritaire que l’espace, par exemple « \ », nous utiliserons des parenthèses, comme usuellement en arithmétique ou en algèbre, par exemple dans « \(c\)1 (\(c\)2 \ \(c\)3) ». Cette expression calcule ainsi l’union de \(c\)1 et « \(c\)2\ \(c\)3 », alors que, d’après nos règles de priorités :
- « \(c\)1 \(c\)2 \ \(c\)3 » est identique à « (\(c\)1 \(c\)2) \ \(c\)3 »
- « \(c\)1 \ \(c\)2 \(c\)3 » est identique à « \(c\)1 \ (\(c\)2 \(c\)3) »
Conjonctions
Enfin, dans le cas général, nos propositions conjonctives sont des ensembles finis de clauses, écrits sous la forme de liste de clauses séparées par le symbole « \(∧\) ». Par définition, une telle conjonction vaut vrai si et seulement si toutes ses clauses valent vrai. La conjonction vide est écrite « T » et a pour valeur vrai. Autrement dit, chaque « \(∧\) » représente un « et » logique. Par exemple, dans la théorie des \(4\)-reines, l’énoncé « la diagonale de \(21\) à \(43\) doit contenir au plus une reine » peut s’écrire comme la conjonction
Celle-ci exprime en effet que toutes les paires de cases de la diagonale sont mutuellement exclusives : au moins une case de chacune de ces paires ne contient pas une reine. Comme vu précédemment, « \(−21\) \(−32\) » peut s’interpréter comme l’énoncé « si \(21\) vaut vrai alors \(32\) vaut faux » ce qui est aussi équivalent à dire « si \(32\) vaut vrai alors \(21\) vaut faux ». Les méta-variables de conjonctions sont notées \(p\), \(p\)1, \(p\)2, …
Au final, la théorie des \(4\)-reines s’exprime sous la forme d’une conjonction de \(80\) clauses : \(4\) clauses de \(4\) littéraux exprimant qu’il doit y avoir au moins une reine sur chacune des lignes et \(76\) clauses de \(2\) littéraux exprimant toutes les paires de cases mutuellement exclusives. La théorie des \(4\)-reines avec une reine en \(11\) s’exprime sous la forme d’une conjonction de \(81\) clauses : les \(80\) clauses précédentes et la clause réduite au littéral « \(11\) ».
Propositions satisfaisables
Une proposition est satisfaisable si et seulement si elle vaut vrai pour au moins une interprétation des variables. Rappelons que, pour notre logique, une interprétation associe à chaque variable, une valeur vrai ou faux fixée. Dans le cas de la théorie des \(n\)-reines, la satisfaisabilité exprime l’existence d’une solution. Pour garantir qu’une proposition est satisfaisable, il suffit d’exhiber une interprétation des variables et de vérifier que dans toutes les clauses de la proposition, il y a au moins un littéral qui vaut vrai pour cette interprétation. Ici, nous écrirons une telle interprétation sous la forme de l’ensemble de toutes les variables qui valent vrai (dans cette interprétation). Par exemple, la théorie des \(4\)-reines est satisfaisable avec l’interprétation « {\(12\), \(24\), \(31\), \(43\)} » : c’est la solution dessinée sur la figure 1. Sur le même principe, la théorie des \(8\)-reines avec une reine en \(11\) et les cases \(83\) et \(64\) interdites (incluant donc dans la théorie les deux clauses « \(−83\) » et « \(−64\) ») est satisfaisable avec l’interprétation « {\(11\), \(25\), \(38\), \(46\), \(53\), \(67\), \(72\), \(84\)} » dessinée sur la figure 5 (voir plus haut).
Propositions insatisfaisables
Une proposition est insatisfaisable si et seulement si elle vaut faux pour toute interprétation. Dans le cas de la théorie des \(n\)-reines, l’insatisfaisabilité exprime l’absence de solution. Pour la vérifier, il va falloir introduire un langage de preuves formelles.
Nous commençons par définir un calcul sur les clauses qui, étant donné une proposition \(p\) et une clause \(c\), garantit que pour toute interprétation, si \(p\) est vrai pour cette interprétation, alors \(c\) aussi. Autrement dit, ce calcul assurera que \(c\) est bien une conséquence logique de \(p\). Pour garantir que \(p\) est insatisfaisable, il suffira alors de montrer que F est une conséquence logique de \(p\).
Différence de clauses
Soient \(c\)1 et \(c\)2 deux clauses. Notons \(c\)1 \ \(c\)2 la clause obtenue à partir de \(c\)1 en supprimant ses littéraux qui se trouvent aussi dans \(c\)2. Par exemple,
Remarquons que \(c\)1 \ \(c\)2 \(=\) F revient à dire que tous les littéraux de \(c\)1 sont dans \(c\)2. Ce que nous notons \(c\)2 \(⊇\) \(c\)1. Dans ce cas, \(c\)2 est une conséquence logique de \(c\)1 (car tout littéral valant vrai dans \(c\)1 se trouve aussi dans \(c\)2). Remarquons aussi que si \(c\)1 \ \(c\)2 \(=\) \(c\)3 alors \(c\)2 \(⊇\) (\(c\)1 \ \(c\)3) et \(c\)1 = \(c\)3 (\(c\)1 \ \(c\)3). Nous allons utiliser ces propriétés ci-dessous.
Résolution arrière
Notons maintenant \(c\)2 \(⊖\) \(c\)1 la clause égale à « \(c\)2 −(\(c\)1 \ \(c\)2) » si \(c\)1 \ \(c\)2 est réduite à un unique littéral. Par exemple,
\(−1\) \(2\) \(3\) \(⊖\) \(4\) \(2\) \(=\) \(−1\) \(2\) \(3\) \(−4\) et \(−1\) \(2\) \(3\) \(⊖\) \(−5\) \(−1\) \(3\) \(=\) \(−1\) \(2\) \(3\) \(5\)
Cette opération n’est pas définie si la clause \(c\)1\ \(c\)2 n’est pas réduite à un unique littéral. Par convention, l’opération \(c\)2 \(⊖\) \(c\)1 n’est utilisée que lorsqu’elle est bien définie. Pour faciliter la lecture, le littéral de différence est généralement écrit en tête de \(c\)1, et son opposé sera alors écrit en queue dans le résultat.
Supposons \(c\)2 \(⊖\) \(c\)1 bien définie. Soit \(ℓ\) le littéral valant \(c\)1 \ \(c\)2. Et soit \(c\) \(=\) \(c\)1 \ \(ℓ\). D’après les propriétés de la différence de clauses, \(c\)2 \(⊇\) \(c\) et \(c\)1 \(=\) \(ℓ\) \(c\). De plus, par définition, \(c\)2 \(⊖\) \(c\)1 \(=\) \(c\)2 \(−ℓ\). On en déduit que la conjonction (\(c\)2 \(⊖\) \(c\)1) \(∧\) \(c\)1 est égale à (\(c\)2 \(−ℓ\)) \(∧\) (\(ℓ\) \(c\)). Lorsque cette dernière vaut vrai, on en déduit que « si \(ℓ\) vaut vrai alors \(c\)2 vaut vrai sinon \(c\) vaut vrai ». On en conclut que \(c\)2 est une conséquence logique de (\(c\)2 \(⊖\) \(c\)1) \(∧\) \(c\)1. En effet, comme \(c\)2 \(⊇\) \(c\), la clause \(c\)2 est une conséquence logique de \(c\), donc si (\(c\)2 \(⊖\) \(c\)1) \(∧\) \(c\)1 vaut vrai, quelle que soit la valeur de vérité de \(ℓ\), la clause \(c\)2 vaut vrai.
Autrement dit, nous avons montré que « sachant \(c\)1, pour montrer \(c\)2, il suffit de montrer \(c\)2 \(⊖\) \(c\)1 ». C’est une forme de raisonnement dit en arrière, car on part de la conclusion à prouver pour en calculer une cause possible. L’opération \(c\)2 \(⊖\) \(c\)1 effectue ce que nous appelons la « résolution en arrière de \(c\)2 sachant \(c\)1 ». En combinant \(⊖\) et \(⊇\), écrivons maintenant nos premières preuves formelles de théorèmes.
Preuves formelles par chaînes de résolutions
Avec la convention \(c\)3 \(⊖\) \(c\)2 \(⊖\) \(c\)1 \(=\) (\(c\)3 \(⊖\) \(c\)2) \(⊖\) \(c\)1, si la relation « \(c\)\(n+1\) \(⊖\) \(c\)\(n\) \(⊖\) … \(⊖\) \(c\)2 \(⊇\) \(c\)1 » est satisfaite, et que toutes les résolutions intermédiaires sont bien définies, alors \(c\)\(n+1\) est une conséquence logique de la conjonction « \(c\)1 \(∧\) \(c\)2 \(∧\) … \(∧\) \(c\)\(n\) ». Peu importe l’ordre des clauses dans cette conjonction. Par contre, l’ordre importe dans la chaîne de résolutions. Si \(c\)1, \(c\)2, …, \(c\)\(n\) sont elles-mêmes des clauses d’une conjonction \(p\), nous dirons alors que \(c\)\(n+1\) est un théorème de la théorie \(p\).
Par exemple, on peut exprimer que l’énoncé informel « s’il y a une reine en \(11\), alors il y a au moins une reine en \(42\) ou \(43\) » est un théorème de la théorie des \(4\)-reines. Cet énoncé s’écrit sous la forme « \(-11\) \(42\) \(43\) ». Et sa preuve formelle est donnée par
Elle prouve le théorème en combinant \(3\) clauses de la théorie des \(4\)-reines : la clause exprimant qu’il y a au moins une reine sur la ligne \(4\) et les deux clauses exprimant que s’il y a une reine en \(11\) alors il n’y a pas de reine ni en \(41\) ni en \(44\).
Pour vérifier que cette preuve est correcte, il faut d’abord vérifier que toutes les clauses utilisées, en dehors de la clause à prouver, sont dans la théorie. Ensuite, il faut effectuer les calculs de la chaîne de résolutions en vérifiant que les opérations de résolution sont bien définies. Enfin, il faut vérifier que la clause obtenue, ici « \(-11\) \(42\) \(43\) \(41\) \(44\) », contient l’ensemble des littéraux de « \(42\) \(43\) \(41\) \(44\) ». C’est bien le cas ici.
En s’inspirant de la preuve visuelle de la figure 4, on peut prouver l’énoncé informel « il n’y a pas de reine en \(22\) » (pour le problème des \(4\)-reines de base). C’est le théorème formel « \(-22\) » dont la preuve formelle est :
La chaîne de résolutions produit ici la clause « \(-22\) \(11\) \(12\) \(13\) \(-14\) \(31\) \(32\) \(33\) \(34\) ».
L’intérêt de ce format de preuve, c’est qu’il n’exige pas d’écrire le résultat des résolutions intermédiaires : celles-ci sont directement calculées par le vérificateur de preuve. En même temps, les calculs du vérificateur sont très faciles et très rapides à effectuer.
Preuves formelles par suites de théorèmes
Soit \(p\) une théorie. Si \(c\) est un théorème prouvé dans cette théorie, alors la conjonction \(p\) \(∧\) \(c\) est elle-même une conséquence logique de cette théorie. Nous généralisons maintenant cette notion de théorème en autorisant les chaînes de résolutions à utiliser un théorème précédemment prouvé à partir de la théorie. Concrètement, nous écrirons une telle preuve de théorème comme une séquence de chaînes de résolutions séparées par un point-virgule. Par exemple, considérons la théorie suivante :
Dans cette théorie, le théorème « \(2\) » est démontré par la preuve formelle suivante, qui commence par prouver le théorème intermédiaire « \(2\) \(3\) ».
Là encore, la vérification est très facile et très rapide. Il existe d’autres formats de preuves formelles, encore plus compacts, mais plus complexes à vérifier. Notamment, le format RUP qui est produit très facilement par les solveurs-SAT de l’état de l’art. Ce format consiste à donner uniquement la liste des théorèmes, sans leur preuve sous forme de chaînes de résolution. Celles-ci se retrouvent par un algorithme appelé propagation unitaire (RUP est l’acronyme de Reverse Unit Propagation), qui, pour être au niveau d’efficacité de l’état de l’art, nécessite une représentation des données très astucieuse, dont la formalisation mathématique est complexe (les solveur-SATs modernes étant en effet capables de résoudre en moins d’une heure certains problèmes avec des millions de clauses et de variables).
Méta-théorème (preuves formelles d’insatisfaisabilité)
Soit \(p\) une théorie dont F est un théorème. Alors \(p\) est insatisfaisable.
Preuve
Nous avons déjà justifié dans les paragraphes précédents que tout théorème \(c\) de \(p\) est une conséquence logique de \(p\). Donc F est une conséquence logique de \(p\). Si \(p\) était satisfaisable, alors F le serait aussi. F est insatisfaisable, donc \(p\) aussi.
Il se trouve que la réciproque de ce méta-théorème est aussi démontrable : cela nous garantit que pour toute proposition \(p\) insatisfaisable, il existe une preuve formelle de F. Mais, si nous sommes seulement intéressés à garantir la correction de notre procédé de vérification, cette garantie n’est pas strictement nécessaire. Pour des logiques plus complexes, permettant par exemple de formaliser les entiers naturels, la réciproque du méta-théorème de correction des preuves formelles est même nécessairement fausse. Dans ce cas, la logique est dite incomplète. C’est le fameux premier (méta-méta)théorème d’incomplétude de Gödel.
Preuve formelle de l’absence de solution au problème des \(4\)-reines avec une reine en case \(11\) :
\(-11\) \(32\) \(⊖\) \(-31\) \(-11\) \(⊖\) \(-33\) \(-11\) \(⊖\) \(34\) \(32\) \(31\) \(33\)
\(⊖\) \(-21\) \(-11\) \(⊖\) \(-22\) \(-11\) \(⊖\) \(-23\) \(-34\) \(⊖\) \(-24\) \(-34\) \(⊇\) \(21\) \(22\) \(23\) \(24\) ;
F \(⊖\) \(11\) \(⊖\) \(-41\) \(-11\) \(⊖\) \(32\) \(-11\) \(⊖\) \(-42\) \(-32\) \(⊖\) \(-43\) \(-32\) \(⊖\) \(-44\) \(-11\) \(⊇\) \(41\) \(42\) \(43\) \(44\)
Cette preuve formelle est proche de la preuve par l’absurde donnée en début d’article, même si elles ont un style très différent (la preuve formelle utilisant des raisonnements « en arrière » alors que la preuve verbalisée est rédigée dans un style « en avant »). En particulier, cette preuve formelle est concise : chaque clause de la théorie n’est utilisée qu’au plus une fois. Et, son théorème intermédiaire, de la forme « s’il y a une reine en \(11\) alors il y a une reine en \(32\) », correspond à celui introduit dans la preuve verbalisée.
Preuve formelle de l’unicité de la solution au problème de la figure 2 :
Notre logique permet de montrer que le problème de la figure 2 (voir plus haut) n’a pas d’autre solution que celle donnée à la figure 5 (voir plus haut). Il suffit de prouver l’insatisfaisabilité de la théorie qui ajoute à la théorie initiale une clause interdisant cette solution, comme « \(-25\) \(-38\) \(-46\) \(-53\) \(-67\) \(-72\) \(-84\) » : cette clause exprime qu’il faut trouver un placement des reines qui diffère de celui en figure 5 sur au moins une case. N’importe quel solveur-SAT récent en trouve une preuve formelle en quelques millisecondes.
La figure 6 dans l’encart ci-dessous donne une telle preuve formelle, en utilisant une légère généralisation du format précédent, qui permet de rendre la preuve un peu plus courte. Cette généralisation consiste à autoriser à donner un nom optionnel aux théorèmes. Pour ne pas être confondu avec une variable, un tel nom de théorème doit commencer par une lettre. Il est associé à un théorème via un symbole « : » (voir la syntaxe utilisée par la figure 6, voir encart ci-dessous). Cela autorise les résolutions à utiliser le nom à la place de l’énoncé de son théorème associé. Pour être correcte, une preuve doit seulement contenir des noms de théorème qui sont associés à un théorème et un seul.
Conventions de nommage : « Ln » liste les reines plaçables en ligne \(n\) ; « Hx » et « Ix » sont généralement (mais pas toujours) utilisés pour introduire le littéral \(x\) par résolution arrière (après une différence sur \(−x\)); « Zx » est similaire à « Hx » mais en échangeant \(x\) et \(−x\). Seuls les théorèmes réduits à des littéraux ne sont pas nommés.
L2: 23 24 25 26 27 28 ⊖ 11 ⊖ -21 -11 ⊖ -22 -11 ⊇ 21 22 23 24 25 26 27 28;
L3: 32 34 35 36 37 38 ⊖ 11 ⊖ -31 -11 ⊖ -33 -11 ⊇ 31 32 33 34 35 36 37 38;
L4: 42 43 45 46 47 48 ⊖ 11 ⊖ -41 -11 ⊖ -44 -11 ⊇ 41 42 43 44 45 46 47 48;
L5: 52 53 54 56 57 58 ⊖ 11 ⊖ -51 -11 ⊖ -55 -11 ⊇ 51 52 53 54 55 56 57 58;
L6: 62 63 65 67 68 ⊖ 11 ⊖ -61 -11 ⊖ -64 ⊖ -66 -11 ⊇ 61 62 63 64 65 66 67 68;
L7: 72 73 74 75 76 78 ⊖ 11 ⊖ -71 -11 ⊖ -77 -11 ⊇ 71 72 73 74 75 76 77 78;
L8: 82 84 85 86 87 ⊖ 11 ⊖ -81 -11 ⊖ -83 ⊖ -88 -11 ⊇ 81 82 83 84 85 86 87 88;
H35: -35 63 67 ⊖ -62 -35 ⊖ -65 -35 ⊖ -68 -35 ⊇ L6;
H47: -47 32 34 35 ⊖ -36 -47 ⊖ -37 -47 ⊖ -38 -47 ⊇ L3;
H42: -42 53 56 57 58 73 78 ⊖ -52 -42 ⊖ L5 ⊖ -72 -42 ⊖ -74 -54 ⊖ -75 -42 ⊖ L7 ⊖ -82 -42 ⊖ -84 -54 ⊖ -85 -76 ⊖ -86 -42 ⊖ -87 -54 ⊇ L8;
H68: -68 32 34 35 43 45 53 56 73 78 ⊖ -57 -68 ⊖ -58 -68 ⊖ H42 ⊖ -46 -68 ⊖ -48 -68 ⊖ L4 ⊖ -36 -47 ⊖ -37 -47 ⊖ -38 -68 ⊇ L3;
H38: -38 43 45 47 53 56 63 67 68 73 78 ⊖ -65 -38 ⊖ L6 ⊖ -42 -62 ⊖ -48 -38 ⊖ L4 ⊖ -52 -62 ⊖ -57 -46 ⊖ -58 -38 ⊖ L5 ⊖ -72 -62 ⊖ -74 -38 ⊖ -76 -46 ⊖ L7 ⊖ -82 -62 ⊖ -84 -54 ⊖ -85 -75 ⊖ -86 -46 ⊖ -87 -54 ⊇ L8;
H37: -37 43 45 47 53 56 73 78 ⊖ -46 -37 ⊖ -48 -37 ⊖ L4 ⊖ -57 -37 ⊖ H42 ⊖ -72 -42 ⊖ -75 -42 ⊖ -76 -58 ⊖ L7 ⊖ -82 -37 ⊖ -84 -74 ⊖ -85 -58 ⊖ -86 -42 ⊖ -87 -37 ⊇ L8;
I42: -42 63 67 68 72 73 76 78 ⊖ -62 -42 ⊖ L6 ⊖ -75 -42 ⊖ L7 ⊖ -82 -42 ⊖ -84 -74 ⊖ -85 -74 ⊖ -86 -42 ⊖ -87 -65 ⊇ L8;
-23 ⊖ -63 -23 ⊖ -67 -23 ⊖ H35 ⊖ -32 -23 ⊖ -34 -23 ⊖ H47 ⊖ -43 -23 ⊖ -45 -23 ⊖ -53 -23 ⊖ -56 -23 ⊖ -73 -23 ⊖ -78 -23 ⊖ H37 ⊖ H68 ⊖ H38 ⊖ L3 ⊖ -72 -36 ⊖ -76 -36 ⊖ I42 ⊖ -46 -36 ⊖ L4 ⊖ -75 -48 ⊖ L7 ⊖ -52 -74 ⊖ -54 -36 ⊖ -57 -48 ⊖ -58 -36 ⊇ L5;
H48: -48 25 26 27 63 67 68 72 76 86 ⊖ -23 ⊖ -28 -48 ⊖ L2 ⊖ -74 -24 ⊖ -75 -48 ⊖ -78 -48 ⊖ L7 ⊖ -62 -73 ⊖ L6 ⊖ -82 -73 ⊖ -84 -48 ⊖ -85 -65 ⊖ -87 -65 ⊇ L8;
H43: -43 25 26 27 54 56 58 63 67 68 72 76 86 ⊖ -52 -43 ⊖ -53 -43 ⊖ L5 ⊖ -23 ⊖ -24 -57 ⊖ L2 ⊖ -65 -43 ⊖ L6 ⊖ -82 -62 ⊖ -84 -57 ⊖ -87 -57 ⊖ L8 ⊖ -73 -62 ⊖ -74 -85 ⊖ -75 -57 ⊖ -78 -28 ⊇ L7;
Z68: 68 25 26 27 45 46 47 54 56 58 63 67 72 76 86 ⊖ H43 ⊖ H48 ⊖ L4 ⊖ -52 -42 ⊖ -53 -42 ⊖ L5 ⊖ -62 -42 ⊖ L6 ⊖ -82 -42 ⊖ -84 -57 ⊖ -85 -65 ⊖ -87 -57 ⊇ L8;
H36: -36 47 63 67 ⊖ -25 -36 ⊖ -26 -36 ⊖ -27 -36 ⊖ -45 -36 ⊖ -46 -36 ⊖ -54 -36 ⊖ -56 -36 ⊖ -58 -36 ⊖ -72 -36 ⊖ -76 -36 ⊖ -86 -36 ⊖ Z68 ⊖ -23 ⊖ -24 -68 ⊖ -28 -68 ⊇ L2;
I68: -68 32 34 35 36 ⊖ -38 -68 ⊖ L3 ⊖ -23 ⊖ -24 -68 ⊖ -26 -37 ⊖ -27 -37 ⊖ -28 -68 ⊖ L2 ⊖ -43 -25 ⊖ -45 -25 ⊖ -46 -68 ⊖ H47 ⊖ -48 -68 ⊖ L4 ⊖ -53 -42 ⊖ -57 -68 ⊖ -58 -68 ⊖ -73 -37 ⊖ -78 -68 ⊖ H42 ⊖ -72 -42 ⊖ -74 -56 ⊖ -75 -25 ⊖ -76 -56 ⊇ L7;
H56: -56 32 34 35 63 67 ⊖ -47 -56 ⊖ H36 ⊖ I68 ⊖ -65 -56 ⊖ L6 ⊖ -72 -62 ⊖ -73 -62 ⊖ -74 -56 ⊖ -76 -56 ⊖ -78 -56 ⊖ L7 ⊖ -82 -62 ⊖ -84 -75 ⊖ -85 -75 ⊖ -86 -75 ⊖ -38 -56 ⊖ L3 ⊖ -87 -37 ⊇ L8;
H62: -62 45 46 47 48 56 57 58 ⊖ -42 -62 ⊖ L4 ⊖ -54 -43 ⊖ -52 -62 ⊖ -53 -62 ⊇ L5;
H78: -78 32 34 35 63 67 ⊖ H47 ⊖ H36 ⊖ -38 -78 ⊖ L3 ⊖ -45 -78 ⊖ -46 -37 ⊖ -48 -37 ⊖ -56 -78 ⊖ -57 -37 ⊖ -58 -78 ⊖ H62 ⊖ -68 -78 ⊖ L6 ⊖ -23 ⊖ -25 -65 ⊖ -26 -37 ⊖ -27 -37 ⊖ -28 -78 ⊖ L2 ⊖ -42 -24 ⊖ -43 -65 ⊇ L4;
H65: -65 26 27 28 46 47 48 ⊖ -23 ⊖ -25 -65 ⊖ L2 ⊖ -42 -24 ⊖ -43 -65 ⊖ -45 -65 ⊇ L4;
Z45: 45 -37 47 56 63 67 68 78 ⊖ -26 -37 ⊖ -27 -37 ⊖ -28 -37 ⊖ -46 -37 ⊖ -48 -37 ⊖ H65 ⊖ L6 ⊖ -42 -62 ⊖ L4 ⊖ -52 -62 ⊖ -53 -62 ⊖ -54 -43 ⊖ -57 -37 ⊖ L5 ⊖ -23 ⊖ -25 -58 ⊖ L2 ⊖ -72 -62 ⊖ -73 -37 ⊖ -74 -24 ⊖ -76 -43 ⊖ L7 ⊖ -82 -37 ⊖ -84 -24 ⊖ -85 -58 ⊖ -86 -75 ⊖ -87 -37 ⊇ L8;
I37: -37 47 56 63 67 68 78 ⊖ -26 -37 ⊖ -27 -37 ⊖ -28 -37 ⊖ -46 -37 ⊖ -48 -37 ⊖ H65 ⊖ L6 ⊖ -23 ⊖ Z45 ⊖ -25 -45 ⊖ L2 ⊖ -82 -37 ⊖ -84 -24 ⊖ -85 -45 ⊖ -87 -37 ⊖ L8 ⊖ -52 -62 ⊖ -53 -86 ⊖ -54 -24 ⊖ -57 -37 ⊖ L5 ⊖ -72 -62 ⊖ -73 -37 ⊖ -74 -24 ⊖ -75 -45 ⊖ -76 -58 ⊇ L7;
H45: -45 26 27 28 52 53 56 58 ⊖ -23 ⊖ -25 -45 ⊖ L2 ⊖ -54 -24 ⊖ -57 -24 ⊇ L5;
Z32: 32 34 35 63 67 ⊖ H47 ⊖ H36 ⊖ H56 ⊖ H78 ⊖ I68 ⊖ I37 ⊖ L3 ⊖ -65 -38 ⊖ L6 ⊖ -26 -62 ⊖ -27 -38 ⊖ -28 -38 ⊖ -52 -62 ⊖ -53 -62 ⊖ -58 -38 ⊖ H45 ⊖ -73 -62 ⊖ H38 ⊖ -54 -43 ⊖ L5 ⊖ -72 -62 ⊖ -74 -38 ⊖ -75 -57 ⊖ -76 -43 ⊇ L7;
H28: -28 42 43 45 52 53 54 56 ⊖ -58 -28 ⊖ L5 ⊖ -46 -57 ⊖ -47 -57 ⊖ -48 -28 ⊇ L4;
I62: -62 24 25 43 45 52 54 56 84 ⊖ -42 -62 ⊖ -53 -62 ⊖ H28 ⊖ -23 ⊖ -26 -62 ⊖ L2 ⊖ -57 -27 ⊖ L5 ⊖ -47 -27 ⊖ -48 -58 ⊖ L4 ⊖ -82 -62 ⊖ -85 -58 ⊖ -86 -46 ⊖ -87 -27 ⊇ L8;
H58: -58 43 45 47 62 63 67 72 74 78 84 87 ⊖ -68 -58 ⊖ L6 ⊖ -75 -65 ⊖ -76 -58 ⊖ L7 ⊖ -82 -73 ⊖ -85 -65 ⊖ L8 ⊖ -42 -86 ⊖ -46 -86 ⊖ -48 -58 ⊇ L4;
H27: -27 43 45 52 54 56 62 63 67 74 78 84 ⊖ -47 -27 ⊖ -72 -27 ⊖ -87 -27 ⊖ H58 ⊖ -57 -27 ⊖ L5 ⊖ -73 -53 ⊖ -75 -53 ⊖ L7 ⊖ -85 -76 ⊖ -86 -53 ⊖ L8 ⊖ -42 -53 ⊖ -46 -82 ⊖ L4 ⊖ -65 -76 ⊖ -68 -48 ⊇ L6;
I48: -48 24 25 27 ⊖ -23 ⊖ -26 -48 ⊖ -28 -48 ⊇ L2;
I28: -28 43 45 48 62 63 67 84 ⊖ -82 -28 ⊖ -68 -28 ⊖ L6 ⊖ -85 -65 ⊖ -87 -65 ⊖ L8 ⊖ -42 -86 ⊖ -46 -86 ⊖ L4 ⊖ -32 -65 ⊖ H35 ⊖ Z32 ⊖ -52 -34 ⊖ -53 -86 ⊖ -54 -34 ⊖ -56 -34 ⊖ -57 -47 ⊖ -58 -28 ⊇ L5;
H87: -87 52 53 54 56 62 63 67 ⊖ -65 -87 ⊖ -57 -87 ⊖ L5 ⊖ -68 -58 ⊇ L6;
Z47: 47 43 45 46 48 52 53 54 56 62 63 67 74 78 84 86 ⊖ L4 ⊖ -72 -42 ⊖ -82 -42 ⊖ H87 ⊖ L8 ⊖ -65 -85 ⊖ H58 ⊖ L5 ⊖ -68 -57 ⊇ L6;
H34: -34 63 67 ⊖ -24 -34 ⊖ -25 -34 ⊖ -43 -34 ⊖ -45 -34 ⊖ -52 -34 ⊖ -54 -34 ⊖ -56 -34 ⊖ -84 -34 ⊖ I62 ⊖ -74 -34 ⊖ -78 -34 ⊖ H27 ⊖ I48 ⊖ I28 ⊖ -23 ⊖ L2 ⊖ -46 -26 ⊖ -53 -26 ⊖ -86 -26 ⊖ Z47 ⊖ -57 -47 ⊖ -58 -47 ⊇ L5;
I47: -47 24 28 52 54 57 58 ⊖ -56 -47 ⊖ L5 ⊖ -63 -53 ⊖ -67 -47 ⊖ H34 ⊖ -35 -53 ⊖ Z32 ⊖ -62 -32 ⊖ -65 -32 ⊖ L6 ⊖ -72 -32 ⊖ -73 -53 ⊖ -74 -47 ⊖ -76 -32 ⊖ -78 -68 ⊖ L7 ⊖ -23 ⊖ -25 -75 ⊖ -26 -53 ⊖ -27 -47 ⊇ L2;
Z67: 67 35 63 ⊖ H34 ⊖ Z32 ⊖ -62 -32 ⊖ -65 -32 ⊖ L6 ⊖ -24 -68 ⊖ -28 -68 ⊖ -52 -32 ⊖ -54 -32 ⊖ -57 -68 ⊖ -58 -68 ⊖ I47 ⊖ -42 -32 ⊖ -43 -32 ⊖ -46 -68 ⊖ -48 -68 ⊖ L4 ⊖ -82 -32 ⊖ -85 -45 ⊖ -86 -68 ⊖ -87 -32 ⊖ L8 ⊖ -72 -32 ⊖ -74 -84 ⊖ -75 -45 ⊖ -76 -32 ⊖ -78 -68 ⊖ L7 ⊖ -53 -73 ⊖ -56 -45 ⊇ L5;
H53: -53 24 25 27 43 45 47 ⊖ -42 -53 ⊖ I48 ⊖ L4 ⊖ -82 -46 ⊖ -35 -53 ⊖ -63 -53 ⊖ Z67 ⊖ -85 -67 ⊖ -86 -53 ⊖ -87 -67 ⊖ L8 ⊖ -73 -53 ⊖ -74 -84 ⊖ -75 -84 ⊖ -76 -67 ⊖ -78 -67 ⊖ L7 ⊖ -32 -72 ⊖ -34 -67 ⊖ -36 -46 ⊖ -37 -67 ⊖ -23 ⊖ -26 -46 ⊖ L2 ⊖ -38 -28 ⊇ L3;
Z25: 25 24 27 34 35 37 43 45 47 52 56 57 58 85 87 ⊖ H53 ⊖ L5 ⊖ -32 -54 ⊖ -36 -54 ⊖ L3 ⊖ -23 ⊖ -28 -38 ⊖ L2 ⊖ -46 -26 ⊖ I48 ⊖ L4 ⊖ -82 -42 ⊖ -84 -54 ⊖ -86 -42 ⊇ L8;
H24: -24 52 56 57 58 76 78 85 87 ⊖ -84 -24 ⊖ -54 -24 ⊖ L5 ⊖ -86 -53 ⊖ L8 ⊖ -72 -82 ⊖ -73 -53 ⊖ -74 -24 ⊖ -42 -24 ⊖ -43 -53 ⊖ -35 -24 ⊖ -63 -53 ⊖ Z67 ⊖ -45 -67 ⊖ -46 -24 ⊖ -47 -67 ⊖ L4 ⊖ -75 -48 ⊇ L7;
H82: -82 34 35 36 37 73 75 76 78 ⊖ -52 -82 ⊖ -72 -82 ⊖ L7 ⊖ -54 -74 ⊖ -63 -74 ⊖ Z67 ⊖ -56 -67 ⊖ -57 -67 ⊖ -58 -67 ⊖ L5 ⊖ -42 -82 ⊖ -43 -53 ⊖ -45 -67 ⊖ -46 -82 ⊖ -47 -67 ⊖ L4 ⊖ -32 -82 ⊖ -38 -48 ⊇ L3;
I53: -53 -25 -67 35 43 ⊖ -34 -67 ⊖ -36 -25 ⊖ -37 -67 ⊖ -73 -53 ⊖ -75 -25 ⊖ -76 -67 ⊖ -78 -67 ⊖ H82 ⊖ -85 -67 ⊖ -86 -53 ⊖ -87 -67 ⊖ L8 ⊖ -74 -84 ⊖ L7 ⊖ -32 -72 ⊖ L3 ⊖ -42 -53 ⊖ -45 -67 ⊖ -47 -67 ⊖ -48 -84 ⊖ L4 ⊇ -25 -38 -46 -53 -67 -72 -84;
Z43: 43 -67 35 52 ⊖ -56 -67 ⊖ -57 -67 ⊖ -58 -67 ⊖ -76 -67 ⊖ -78 -67 ⊖ -85 -67 ⊖ -87 -67 ⊖ H24 ⊖ -27 -67 ⊖ -34 -67 ⊖ -37 -67 ⊖ -45 -67 ⊖ -47 -67 ⊖ Z25 ⊖ I53 ⊖ L5 ⊖ -72 -54 ⊖ -74 -54 ⊖ -75 -25 ⊖ L7 ⊖ -32 -54 ⊖ -36 -25 ⊖ L3 ⊖ -82 -73 ⊖ -84 -54 ⊖ L8 ⊖ -42 -86 ⊖ -46 -86 ⊖ -48 -38 ⊇ L4;
Z52: 52 -67 35 ⊖ Z43 ⊖ -53 -43 ⊖ -54 -43 ⊖ -56 -67 ⊖ -57 -67 ⊖ -58 -67 ⊇ L5;
H86: -86 32 34 35 37 42 43 45 47 ⊖ -36 -86 ⊖ -46 -86 ⊖ L4 ⊖ -38 -48 ⊇ L3;
Z35: 35 -67 ⊖ Z52 ⊖ -82 -52 ⊖ -85 -67 ⊖ -32 -52 ⊖ -34 -67 ⊖ -37 -67 ⊖ -42 -52 ⊖ -43 -52 ⊖ -45 -67 ⊖ -47 -67 ⊖ H86 ⊖ -87 -67 ⊖ L8 ⊖ -23 ⊖ -24 -84 ⊖ -25 -52 ⊖ -27 -67 ⊖ I48 ⊖ L4 ⊖ -26 -46 ⊖ L2 ⊖ -73 -28 ⊖ -72 -52 ⊖ -74 -52 ⊖ -75 -84 ⊖ -76 -67 ⊖ -78 -67 ⊇ L7;
I78: -78 52 53 54 57 ⊖ -56 -78 ⊖ -58 -78 ⊇ L5;
H84: -84 52 53 54 72 73 74 ⊖ -75 -84 ⊖ -57 -84 ⊖ I78 ⊖ L7 ⊖ -56 -76 ⊖ -58 -76 ⊇ L5;
H57: -57 43 45 84 85 ⊖ -46 -57 ⊖ -47 -57 ⊖ -48 -57 ⊖ L4 ⊖ -82 -42 ⊖ -86 -42 ⊖ -87 -57 ⊇ L8;
I58: -58 27 43 45 72 73 74 78 ⊖ -76 -58 ⊖ L7 ⊖ -42 -75 ⊖ -47 -58 ⊖ -48 -75 ⊖ L4 ⊖ -23 ⊖ -24 -46 ⊖ -25 -58 ⊖ -26 -46 ⊖ -28 -58 ⊇ L2;
-63 ⊖ -52 -63 ⊖ -53 -63 ⊖ -54 -63 ⊖ -72 -63 ⊖ -73 -63 ⊖ -74 -63 ⊖ H84 ⊖ -43 -63 ⊖ -45 -63 ⊖ -85 -63 ⊖ H57 ⊖ I78 ⊖ -27 -63 ⊖ I58 ⊖ L5 ⊖ -76 -56 ⊖ L7 ⊖ -42 -75 ⊖ -46 -56 ⊖ -47 -56 ⊖ -48 -75 ⊇ L4;
67 ⊖ -63 ⊖ H35 ⊇ Z67;
F ⊖ 67 ⊖ Z35 ⊖ -23 ⊖ -24 -35 ⊖ -25 -35 ⊖ -26 -35 ⊖ -27 -67 ⊖ L2 ⊖ -45 -67 ⊖ -46 -35 ⊖ -47 -67 ⊖ I48 ⊖ -53 -35 ⊖ -56 -67 ⊖ -57 -67 ⊖ -58 -67 ⊖ -73 -28 ⊖ -78 -67 ⊖ H42 ⊖ L4 ⊖ -52 -43 ⊖ -54 -43 ⊇ L5
Pour un être humain, vérifier la preuve formelle en figure 6 est long et fastidieux (contre moins de 1 milliseconde avec les vérificateurs automatiques de type SatAns-Cert). Cette pénibilité rend le risque d’erreur d’inattention très probable. Nous touchons ici aux limites des preuves complètement formalisées : elles sont parfaitement adaptées à la vérification par une machine, mais pas vraiment aux humains, dont les capacités de calcul sont plus faibles et moins fiables. C’est une des raisons pour lesquelles les mathématiciens, quand ils rédigent des preuves pour d’autres humains, ne rédigent pas dans un style complètement formalisé : il est préférable de faire (modérément) appel aux capacités de « compréhension » des lecteurs et lectrices via leurs différentes aptitudes (visualisation 2D, analogies, abstractions, etc.) plutôt que de reposer intégralement sur leurs capacités de calcul. De même, un énoncé formel, s’il est destiné à être compris par les humains, doit contenir des explications informelles en commentaires, comme n’importe quel code informatique. C’est finalement la complémentarité entre le texte formel et ses explications informelles qui permet d’éviter les erreurs.
Heuristique versus vérification des problèmes SAT
En résumé, nous avons défini ci-dessus un procédé automatisable de vérification des solutions (ou d’absence de solution) aux problèmes encodables en logique des propositions à variables booléennes ; ce qui inclut les \(n\)-reines, les sudokus et bien d’autres choses. Ce procédé a l’avantage d’être beaucoup plus simple que les heuristiques de résolution dans cette logique, appelées communément solveurs-SAT.
Esquissons un peu une famille d’heuristiques de solveur-SAT très courante, appelée CDCL (pour « Conflict Driven Clause Learning », ou en français « apprentissage de clause par analyse de conflit »). Étant donné une théorie, un solveur-SAT donne soit un modèle de cette théorie, c’est-à-dire une interprétation des variables dans laquelle la théorie vaut vrai, soit une garantie que la théorie est insatisfaisable. Les heuristiques CDCL procèdent par « essai-échec » en construisant progressivement un modèle partiel de la théorie : c’est-à-dire une interprétation d’un sous-ensemble (initialement vide) des variables pour laquelle aucune des clauses de la théorie ne vaut faux. Par définition, une clause, dont tous les littéraux ont une valeur de vérité déterminée par le modèle partiel, a elle la valeur vrai (puisque la clause a une valeur déterminée qui ne vaut pas faux). Et, si toutes les clauses ont ainsi une valeur déterminée, la théorie est donc satisfaite par le modèle. Au contraire, tant qu’il reste des clauses qui ont une valeur de vérité indéterminée par le modèle partiel courant, l’heuristique est amenée à choisir un littéral qui rend certaines d’entre elles vraies, pour tenter d’ajouter ce littéral au modèle partiel courant.
En fait, le paradigme CDCL cherche à éviter les nombreux calculs inutiles inhérents à cette approche « essai-échec ». Aussi, elle ne procède au choix d’essayer un nouveau littéral qu’après avoir soigneusement analysé les clauses de valeur indéterminée dans le modèle partiel courant. En particulier, elle recherche les clauses dites unitaires, c’est-à-dire dont la valeur est indéterminée à cause d’un unique littéral (ce sont donc les clauses dont tous les littéraux valent faux dans le modèle courant sauf un unique littéral qui reste indéterminé). L’heuristique sélectionne alors un tel littéral de manière prioritaire puisque c’est en quelque sorte une conséquence nécessaire des choix de littéraux antérieurs. Ainsi, les heuristiques CDCL pratiquent la propagation unitaire déjà mentionnée précédemment : cet algorithme correspond à sélectionner en cascade les littéraux à partir de clauses unitaires jusqu’à aboutir soit sur un modèle partiel sans clause unitaire, soit sur une clause valant faux dans l’interprétation partielle courante. Illustrons ci-dessous ces idées sur le problème des \(4\)-reines en supposant que le premier littéral choisi soit \(11\). La propagation unitaire sélectionne alors tous les littéraux \(ℓ\) qui apparaissent dans une clause « \(ℓ\) \(-11\) » de la théorie (ce sont des clauses unitaires dans l’interprétation partielle contenant uniquement le littéral « \(11\) »).
À l’issue de cette propagation unitaire, l’état du modèle partiel est représenté sur l’échiquier de gauche. Supposons ensuite que le deuxième littéral choisi soit \(−32\). Dans cette nouvelle interprétation partielle, la clause « \(31\) \(32\) \(33\) \(34\) » a un unique littéral indéterminé \(34\), qui est donc sélectionné par la propagation unitaire. Celle-ci aboutit alors à l’interprétation partielle représentée sur l’échiquier de droite où la clause « \(21\) \(22\) \(23\) \(24\) » vaut faux.
Dans le cas où la propagation unitaire aboutit à un modèle partiel sans clause unitaire, soit il ne reste aucune clause indéterminée et la théorie est donc satisfaite, soit les clauses non satisfaites restent indéterminées à cause d’au moins deux littéraux (comme dans l’échiquier de gauche ci-dessous).
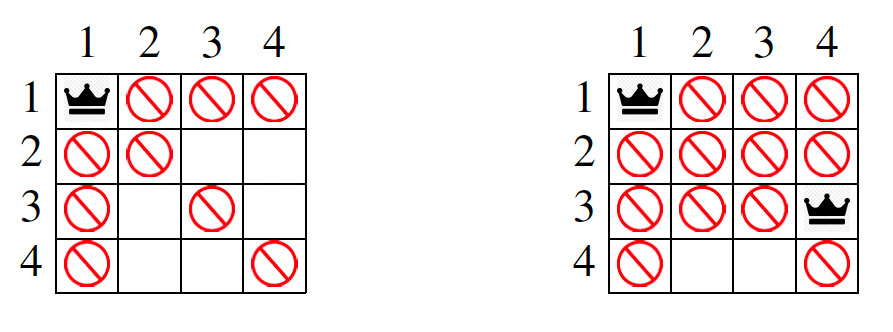
Dans ce second cas, les heuristiques CDCL guident alors leur choix d’un nouveau littéral grâce à des analyses statistiques (prenant en compte la fréquence des littéraux et de leur opposé dans la théorie, leur utilisation par l’heuristique jusqu’ici, etc.). Il y a ici beaucoup de stratégies possibles, entraînant une grande diversité d’heuristiques CDCL.
Sinon, la propagation unitaire aboutit à un contre-modèle de la théorie initiale, c’est-à-dire à une interprétation (partielle) dans laquelle la théorie vaut faux (comme dans l’échiquier de droite ci-dessus). C’est la situation désignée comme « échec » dans l’encart sur l’approche par essai-échec, mais qui s’appelle en fait « conflit » en résolution SAT . Techniquement, ce contre-modèle peut être vu comme une conjonction de littéraux, qui force donc les variables de ces littéraux à prendre une valeur de vérité fixée. Par exemple, sur l’échiquier de droite ci-dessus, ce contre-modèle correspond à la conjonction « \(11\) \(∧\) \(-12\) \(∧\) … \(∧\) \(-33\) \(∧\) \(34\) \(∧\) \(-41\) \(∧\) \(-44\) ». Pour des raisons d’efficacité détaillées plus loin, l’heuristique commence par minimiser le contre-modèle modulo propagation unitaire : elle ne conserve qu’une conjonction minimale de littéraux qui rend la théorie fausse (après propagation unitaire) – c’est « l’analyse du conflit ». Sur l’exemple, « \(11\) \(∧\) \(-32\) » (l’interprétation réduite aux littéraux choisis) est un tel contre-modèle minimal. Autrement dit, en appelant \(p\) la théorie des \(4\)-reines, si « \(11\) \(∧\) \(-32\) » vaut vrai alors \(p\) vaut faux. C’est logiquement équivalent à dire que si \(p\) vaut vrai alors « \(11\) \(∧\) \(-32\) » vaut faux et donc que la clause « \(-11\) \(32\) » vaut vrai. Plus généralement, la clause formée de l’opposé des littéraux du contre-modèle correspond toujours à une conséquence logique de la théorie initiale. L’ajouter à la théorie est logiquement équivalent à considérer la théorie initiale. Et c’est ce que fait une heuristique CDCL : elle étend la théorie avec cette clause « apprise de l’analyse d’un conflit » avant de repartir d’un modèle partiel antérieur qui ne rend pas fausse cette clause apprise (si un tel modèle partiel n’existe pas, c’est que la clause apprise est F, et que la théorie initiale est insatisfaisable). Cela revient à mémoriser le contre-modèle dans la théorie (en l’interdisant explicitement) pour éviter d’en refaire le calcul plusieurs fois. Sur l’exemple, l’heuristique CDCL ajoute donc la clause « \(-11\) \(32\) » à la théorie des \(4\)-reines et repart avec le modèle partiel correspondant à l’échiquier de gauche (issu de la propagation unitaire après le choix de « \(11\) »). La nouvelle clause est alors unitaire dans ce modèle ; la propagation unitaire sélectionne donc « \(32\) » et aboutit finalement à un conflit avec la clause « \(41\) \(42\) \(43\) \(44\) ». De ce conflit, l’heuristique CDCL apprend finalement la clause « \(-11\) » et repart avec un modèle partiel vide, etc.
En résumé, le paradigme CDCL permet, modulo des « bons » choix de littéraux, de découvrir automatiquement le raisonnement schématisé à la figure 3. Il y a aussi d’autres optimisations que peuvent faire les heuristiques CDCL, notamment la suppression de clauses de la théorie estimées redondantes (par exemple de clauses apprises), etc. Pour plus de détails, consulter la bible sur le sujet : Handbook of Satisfiability (Second Edition – April 2021 – IOS Press).
Programmation défensive formellement vérifiée
Le constat que « la vérification est généralement nettement plus facile que la recherche » inspire un paradigme de conception de logiciels par programmation défensive, où la recherche de solution est effectuée par un oracle basé sur des heuristiques efficaces, mais jugé potentiellement non fiable, et où un vérificateur rigoureux se charge de valider la correction des résultats, en signalant les résultats non validés quand il y en a. Ce paradigme est notamment très utile dans les outils de développement des logiciels, comme les compilateurs qui traduisent un programme « source » écrit dans un langage de haut niveau, en code machine optimisé pour un processeur donné. En effet, un bug dans le compilateur pourrait introduire un bug dans le code machine généré, à l’insu des développeurs et développeuses. Dans ce contexte, la programmation défensive cherche à vérifier que le code machine est conforme au programme source. Quand ce n’est pas le cas, la compilation échoue, ce qui est beaucoup moins problématique que de produire silencieusement un code machine incorrect. Ainsi, en pratique, la programmation défensive est appliquée sur des problèmes SAT, mais aussi sur des problèmes très différents. Pour chaque famille de problèmes, il faut donc inventer des techniques de vérification adaptées, qui peuvent se révéler très différentes du cas des problèmes SAT. Par exemple, la vérification de compilateur s’appuie (entre autres) sur des techniques d’exécution symbolique.
En génie logiciel, la programmation défensive consiste à intégrer des vérifications à l’exécution d’un logiciel qui détectent certains comportements « inattendus » et permettent d’empêcher le logiciel de continuer son exécution comme si de rien n’était. Au contraire, généralement, lorsqu’un tel comportement est détecté, le logiciel est stoppé avec un message d’erreur qui aide à identifier le problème. Cette pratique aide donc à détecter, localiser et identifier des bugs. Elle empêche surtout certains bugs de rester inaperçus des programmeurs et des utilisateurs du logiciel.
Vérification formelle
Lorsque la correction des résultats est vraiment critique (notamment si les « résultats » sont eux-mêmes des logiciels critiques), vérifier formellement le vérificateur lui-même apporte une sécurité supplémentaire. C’est ce qui s’appelle la programmation défensive formellement vérifiée, de l’acronyme PDFV. Concrètement, il s’agit de prouver formellement que l’implémentation du vérificateur est correcte. Cela nécessite aussi de formaliser sa métathéorie (par exemple, la métathéorie de la vérification en logique propositionnelle exposée à la section précédente). Le tout dans une logique formelle vérifiée par ordinateur. Ce serait de toute façon trop laborieux (et par conséquent pas réellement convaincant) à vérifier en mode « papier/crayon ». Des assistants à la preuve formelle tels que Coq ou Isabelle ont permis d’appliquer la PDFV à des logiciels « complexes », comme des solveurs-SAT de l’état de l’art. En particulier, ces assistants de preuve ont permis d’appliquer la PDFV à des logiciels avec des spécifications complexes (la spécification d’un logiciel décrit ce que doit faire le logiciel : c’est en quelque sorte un « mode d’emploi » complètement détaillé), comme le compilateur optimisant CompCert (formalisé en Coq) ou le système d’exploitation sécurisé seL4 (formalisé en Isabelle).
Expliquons maintenant la PDFV des solveurs-SAT CDCL. Cette discussion s’inspire de deux logiciels. Premièrement, SatAnsCert un vérificateur formellement vérifié en Coq des réponses de solveurs-SAT, développé à l’été 2018, par Thomas Vandendorpe et moi-même pendant son stage d’étudiant en 3e année de licence. Le mérite principal de ce logiciel est de montrer qu’il est possible de certifier les solveurs-SAT de l’état de l’art en 2018 de manière légère, c’est-à-dire avec environ 1000 lignes de formalisation Coq (scripts de preuve inclus) et quelques semaines de travail. Deuxièmement, le vérificateur Grat de Peter Lammich, formellement vérifié en Isabelle, qui est significativement plus efficace (mais plus complexe) que SatAnsCert.
Leur principe est très simple. Étant donnée une proposition conjonctive de booléens \(p\) (écrite dans un certain fichier), un solveur-SAT CDCL cherche à retourner :
(1) soit une interprétation des variables qui doit donc permettre de vérifier que \(p\) est satisfaisable ; (2) soit une liste de clauses apprises qui doit permettre de prouver que \(p\) est insatisfaisable, et donc en particulier contenir la clause F. Un solveur-SAT peut aussi échouer à résoudre le problème, à cause d’un manque de place mémoire, ou d’un temps de calcul trop long, ou d’un bug interne, etc. Ici, nous nous intéressons uniquement à garantir que les réponses données par le solveur-SAT en cas de succès sont correctes.
Dans le cas (1), il suffit de vérifier que la proposition s’évalue sur « vrai » dans l’interprétation fournie par le solveur-SAT. Formaliser et prouver la correction de ce vérificateur est très facile. De plus, le surcoût en temps d’exécution de cette vérification par rapport au solveur-SAT est complètement négligeable. Par exemple dans les figures ci-dessous, chacun des points représente une parmi 120 propositions satisfaisables de la compétition SAT 2018. L’abscisse de chaque point donne une de ses tailles : nombre de clauses dans la figure du haut, versus nombre de littéraux dans celle du bas. Son ordonnée donne un de ses temps de calcul : pour les points de couleur orange, le temps du solveur-SAT, en l’occurrence CaDiCaL (un des plus rapides en 2018), versus pour les points de couleur verte, le temps du vérificateur de SatAnsCert. Abscisse et ordonnées sont en échelle logarithmique. Ces mesures montrent que non seulement le temps de calcul du vérificateur est infime par rapport au temps du solveur-SAT, mais aussi que ce premier, au contraire du second, est fortement corrélé à la « taille » du problème.
 |
|||
 |
|||
Comparaison expérimentale des temps de calcul d’un solveur et d’un vérificateur pour des théories satisfaisables en fonction de la taille de la théorie (en nombre de clauses, figure du haut – ou en nombre de littéraux, figure du bas). |
|||
Le cas (2) est plus complexe. À partir de la liste de clauses apprises, il faut commencer par construire une preuve de F, ce qui demande encore une algorithmique sophistiquée, surtout qu’il est important d’obtenir une preuve élaguée de théorème intermédiaire inutile (pour économiser l’espace mémoire). Par contre, cet outil intermédiaire, qui transforme un « squelette de preuve » en une « preuve détaillée », n’a pas besoin d’être lui-même formellement vérifié.
Seul le vérificateur de la « preuve détaillée » nécessite d’être formellement vérifié, ce qui dans le cas de SatAnsCert est assez simple. Le surcoût en temps d’exécution de la vérification de la preuve trouvée par le solveur-SAT n’est là pas négligeable. Ainsi, la vérification effectuée par Grat prend souvent un temps comparable à celui pris par le solveur-SAT, mais parfois un temps jusqu’à 4 fois plus long (voir https://satcompetition.github.io/2023/downloads/proposals/grat.pdf). Ces temps peuvent être multipliés par 2 ou 3 dans le cas de SatAnsCert. Ces surcoûts semblent en grande partie induits par l’imposante taille (en gigaoctets) des preuves détaillées : celles-ci transitent en effet par le système de fichiers de l’ordinateur, qui est de beaucoup plus grande taille que la mémoire vive du processeur, mais dont les accès en lecture/écriture sont beaucoup plus lents. Malgré ça, le surcoût de la vérification semble acceptable : le quotient du temps d’exécution du vérificateur par celui du solveur-SAT reste borné par une (petite) constante. Cela correspond à ce qui était naïvement espéré : le vérificateur n’effectue que des calculs déjà faits par le solveur-SAT.
Assistants de preuve
En fait, les logiciels Coq et Isabelle sont eux-mêmes réalisés en programmation défensive. Ils offrent tous les deux des heuristiques puissantes pour construire des preuves formelles, mais utilisent un vérificateur assez réduit pour garantir que ces heuristiques ne permettent pas de prouver des théorèmes faux. Certains prototypes expérimentaux de ces logiciels ont même pu partiellement s’autovérifier (ce qui bien sûr n’offre pas une garantie absolue). C’est donc une forme de PDFV réflexive. Depuis plusieurs dizaines d’années que ces deux logiciels existent, nous avons maintenant un certain recul sur la quantité de bugs critiques (c’est-à-dire qui permettent potentiellement de prouver des théorèmes faux) découverts dans ces logiciels. Il est extrêmement faible : pour Coq, de l’ordre de un par an en moyenne. Dans ces conditions, étant donné de plus le caractère interactif des preuves formelles dans ces assistants de preuve, il est extrêmement peu probable qu’un de leurs bugs critiques permette aux utilisateurs et utilisatrices de prouver un théorème faux sans que ces derniers ne s’en aperçoivent.
Base informatique de confiance (Trusted Computing Base)
Par construction, les bugs de correction d’un logiciel en PDFV ne peuvent que se trouver dans un sous-ensemble très réduit du logiciel qui s’appelle la base informatique de confiance (TCB pour Trusted Computing Base en anglais). Celle-ci comprend surtout la formalisation des spécifications (par exemple, dans le cas de CompCert, les langages de programmation d’entrée et de sortie du compilateur), et éventuellement les composants du logiciel non couverts par la PDFV.
Les TCB de SatAnsCert et Grat sont assez comparables. Elles comprennent l’assistant de preuve (et le compilateur de programmes prouvés avec cet assistant) ; la spécification formelle des solveurs-SAT (quelques dizaines de lignes dans la logique formelle de l’assistant de preuves, définissant essentiellement la représentation des propositions conjonctives et leur satisfaisabilité) ; un composant logiciel (dont le code source fait quelques dizaines de lignes) qui lit la suite des caractères du fichier d’entrée et la convertit dans la représentation formalisée des propositions (définissant, par exemple, une proposition comme une liste de clauses où chaque clause est un ensemble de littéraux, chaque littéral étant un entier non nul) ; et enfin, la partie « principale » du logiciel (dont le code source fait aussi quelques dizaines de lignes) qui enchaîne les appels aux différents composants du logiciel, dont le vérificateur, et affiche le résultat.
Pour compléter, listons les composants logiciels exclus de la TCB : le vérificateur et sa (méta)preuve formelle, mais aussi le solveur-SAT (des dizaines de milliers de lignes de code pour un solveur-SAT de l’état de l’art) et les outils de transformation des preuves retournées par le solveur-SAT via le système de fichiers, dont la correction correspond au succès final du vérificateur.
Même si le nombre de lignes d’un fragment de code n’est qu’une indication très grossière de sa « complexité », c’est une mesure simple qui en donne un premier aperçu. Pour ces solveurs-SAT en PDFV, si on ne considère que le code source spécifique au logiciel (et pas les outils, compilateurs ou assistants de preuves, qui traitent ce code source), on peut estimer que la taille (en nombre de lignes) de la TCB est d’un ordre de grandeur 100 fois plus petit que celle du reste du logiciel. Et la technique de programmation défensive permet d’obtenir une taille de texte en logique formelle (incluant définitions, énoncés et scripts de preuve) d’un ordre de grandeur 10 fois plus petit que le reste du code source.
Dans le cas de CompCert, les spécifications formelles sont complexes : elles nécessitent plusieurs milliers de lignes de code Coq. Mais beaucoup moins que le reste du logiciel qui comprend des centaines de milliers de lignes de code. Depuis plus de quinze ans d’existence, ses bugs critiques — rappelons que dans le cas de CompCert, ils correspondent à des bugs introduits silencieusement par le compilateur dans le programme compilé, à partir d’un programme source sans bug — sont exclusivement apparus dans sa TCB, et jamais dans une partie couverte par la PDFV. Et c’est une très bonne nouvelle, car la TCB est non seulement moins complexe que le reste du logiciel, mais elle évolue aussi beaucoup plus lentement (par exemple, la définition d’un langage de programmation évolue beaucoup plus lentement que l’implémentation de son compilateur). Finalement, le nombre de bugs critiques dans CompCert est lui-même très faible : moins d’une dizaine par an (très rapidement corrigés) contre plusieurs centaines (qui restent la plupart du temps non corrigés pendant plusieurs mois — les optimisations responsables étant par exemple simplement désactivées) pour des compilateurs traditionnels comme GCC ou LLVM.
Note de l’auteur : D’après l’étude « An empirical study of optimization bugs in GCC and LLVM » de Zhide Zhou et ses coauteurs en 2020, les développeurs et développeuses de GCC et LLVM prennent plus d’un an en moyenne pour corriger un bug critique d’optimisation. Dans mon expérience, une correction de bug critique dans la TCB de CompCert ne prend généralement que quelques jours.
En conclusion, la PDFV est une méthode effective pour rendre les logiciels beaucoup plus fiables, en complément des méthodes traditionnelles du génie logiciel. Pour la généraliser, il faut inventer les techniques de vérification défensive adaptées aux heuristiques de l’état de l’art dans chaque domaine d’application.
Le manuscrit d’Habilitation à Diriger des Recherches (HDR) de l’auteur est disponible en anglais « Programmation défensive formellement vérifiée (calculs efficaces et vérifiés en Coq, à partir d’oracles OCaml potentiellement non fiables) ».
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Sylvain Boulmé
Maître de conférences à Grenoble-INP Ensimag et au laboratoire Verimag de l'Université Grenoble Alpes.

