Construire une machine quantique

Le rôle déterminant d’un support physique

La possibilité de donner et de combiner des instructions suppose qu’on a une machine capable de les exécuter. Il faut pour cela un support physique concret. Un calcul donné peut être plus ou moins difficile à effectuer selon le comportement du support physique utilisé, c’est-à-dire selon les instructions qu’il est capable de représenter et combiner efficacement.

Ainsi, notre cerveau, dont le fonctionnement physique sur base de neurones oscillants n’est pas totalement compris, est capable de reconnaître presque instantanément des multitudes d’objets à partir de données visuelles ; pour un ordinateur standard, dont le fonctionnement physique est basé sur le basculement de « bits logiques » (rappel ci-dessous), cette tâche demeure très difficile : le résultat désiré ne peut s’obtenir qu’au prix d’un enchaînement compliqué d’un énorme nombre de ses opérations élémentaires. À l’inverse, un simple ordinateur portable peut manipuler très rapidement des tableaux de nombres et simuler l’évolution de processus compliqués, avec une précision que nos cerveaux n’atteindraient pas en une vie entière. Le but de l’ordinateur quantique est de proposer un nouveau support physique, capable de faciliter des calculs qui sont extrêmement difficiles sur les ordinateurs actuels. Il se servira pour cela d’une propriété physique inexploitée jusqu’ici — la très fragile « phase quantique ». Le prix à payer est de concevoir une machine où cette nouvelle propriété physique a un comportement fiable.

Voyons donc par quels principes nous pouvons construire des machines de calcul fiables, en partant du calculateur analogique, en passant par le calculateur numérique (aussi appelé « digital », nos ordinateurs actuels) jusqu’au calculateur quantique.

Les limites de fiabilité d’un calculateur analogique

Un simple « miaou » peut contenir une infinité de nuances, mais sont-elles toutes bien maitrisées ? Il ne paraît pas réaliste d’exiger une précision infinie à la machine qui exécute nos instructions…

À défaut de dresser des chats, considérons un support physique petit et manipulable, par exemple des électrons. En particulier, imaginons une machine utilisant un seul électron, positionné précisément au début, auquel nous appliquerions des déplacements par un système d’électro-aimants et dont nous mesurerions la position finale. Cela pourrait permettre par exemple de calculer la trajectoire d’une fusée en fonction des accélérations données par ses moteurs. L’accélération serait remise à l’échelle ainsi que l’influence des étoiles et planètes pour déplacer l’électron. Cette machine, une fois construite, permettrait à bas coût de transformer n’importe quelle commande des moteurs en résultat « position à l’instant t ». Cependant, sa fiabilité est douteuse. En effet, il sera très difficile de s’assurer qu’aucun élément extérieur ne vienne perturber notre petit électron durant son trajet ; de plus, une petite erreur d’accélération de notre part, sur ces si petites intensités, peut envoyer l’électron « dans les choux » à long terme. Une impasse semble apparaître : soit on construit une machine où une petite erreur peut tout brouiller, soit on blinde le système contre les influences extérieures mais alors il nous faudra un effort considérable pour le piloter — comme la fusée elle-même finalement. Bien que beaucoup d’améliorations peuvent être apportées pour contrôler les électrons via une telle machine dite « analogique », la solution la plus usuelle pour se protéger des erreurs est actuellement d’utiliser un calculateur dit « numérique » (comme nos ordinateurs actuels).

Comment le numérique permet de rendre les ordinateurs actuels fiables

Pour éviter de se tromper, on peut se borner à contrôler quelques propriétés simples : distinguer « miaou » ou « pas miaou », en réponse à une combinaison d’instructions, permet déjà de faire beaucoup de choses.

Figure 1 : Représentation des deux valeurs 1 («V») ou 0 («F») d’un bit.

Dans nos ordinateurs actuels, les électrons ne peuvent plus prendre qu’un petit nombre de positions, en fait seulement 2, comme un interrupteur. Une position représente le symbole « 0 » ou « F(aux) » (ou « pas miaou »), l’autre « 1 » ou « V(rai) » (ou « miaou »), on parle d’un « bit » d’information. La position de la fusée n’est plus directement visible, mais « encodée » par une suite de « V » et « F », ou de manière équivalente de « 1 » et « 0 » (voir figure 1 ci-à gauche). Par exemple, FVVFVFFV = 01101001 pourrait représenter 0*8+1*4+1*2+0*1, en unités de 10^(1*4+0*2+0*1) mètres et avec le signe 1 = –, soit la coordonnée –60 km. Les opérations physiques à effectuer pour déplacer cette « simulation numérique de la fusée » — à savoir, échanger ou non les valeurs « V » / « F » de chaque bit selon la séquence appropriée — sont une conséquence plus indirecte des accélérations dues aux moteurs, étoiles et planètes. Cependant, on y gagne sur d’autres plans. La machine numérique peut être reprogrammée plus facilement pour faire toute une classe d’autres calculs (voir l’article Comment fonctionne une machine de Turing). Mais surtout, dans ce contexte, elle permet d’éviter des erreurs lorsque des perturbations agissent sur la machine.

Premièrement, de petites imprécisions ne perturberont pas notre interprétation du résultat. En effet, pour chaque position physique de la machine, il suffit d’identifier si l’intention était de représenter « V » ou « F » ; si un électron, initialement placé en « V », se balade un peu sous l’effet de toutes les perturbations extérieures, ce n’est pas grave tant qu’on peut identifier clairement sa zone d’origine. Ceci reste vrai pour le « bit » représentant la centaine de kilomètres de distance, comme pour celui représentant le 5^e chiffre après la virgule. Un tel « encodage » numérique permet donc de s’affranchir de l’impact de petites déviations. Cependant, si rien n’est mis en place pour empêcher l’électron de se balader, il ne restera pas longtemps proche de sa position d’origine.

Ainsi, pour s’assurer que les imprécisions restent petites, et n’impactent donc pas le résultat du calcul numérique, un deuxième élément est souvent essentiel : un « mécanisme de rappel » vers les deux positions particulières représentant « V » et « F ». Un exemple de tous les jours est le ressort qui maintient un interrupteur dans sa position. Pour des électrons, le ressort doit être remplacé par un champ électromagnétique particulier autour des zones « V » et « F ». On peut se représenter cela comme placer l’électron dans une boîte à œufs à 2 places (voir figure 2 ci-dessous) : si une perturbation le pousse à bouger, il retombe dans sa case d’origine. Cette « stabilisation » rend difficile à l’électron la possibilité de s’éloigner de sa valeur « V » ou « F » d’origine. Pour effectuer des calculs, sans tout mélanger, il suffit de tourner lentement d’un demi-tour les boîtes à œufs sélectionnées. En effet, tout au long de ce demi-tour, l’électron suivra sa « case » tout en restant stabilisé dans une zone bien distincte de la valeur inverse ; et lorsqu’on fixe à nouveau la boîte à œufs après un demi-tour, toute la machine se retrouve dans la même situation qu’au départ, sauf que l’électron a échangé sa position « V » ou « F ».

Figure 2 : illustration de la protection par boîte à œufs.

Un troisième élément permettant d’ajouter de la robustesse est l’utilisation d’un « code correcteur d’erreur ». Dans sa version la plus simple, pour dire « V F » on répète « VVVVV FFFFF ». Ainsi, si l’un des électrons bouge trop et saute sur la valeur inverse, on affichera « VVVFV FFFFF » par exemple. On peut alors estimer qu’on avait probablement « VVVVV FFFFF » au départ (dans chaque bloc répétitif la majorité l’emporte) et remettre la machine sur cet état, représentant parfaitement le message « V F », pour la suite du calcul. Cette approche peut d’ailleurs servir à améliorer des simulations « analogiques » également.

En résumé, le mode d’emploi pour obtenir un comportement fiable de votre chat classique (= non-quantique) pourrait être :

1. Se limiter à distinguer s’il est dans la pièce « V » (on entend son « miaou ») ou la pièce « F » (on n’entend pas son « miaou »), plutôt que d’attribuer une importance millimétrée à sa position ;

2. Placer un bol de nourriture dans chaque pièce, pour l’encourager à rester dans la pièce « V » ou « F » qui lui est assignée au départ ;

2’. Afin d’inverser la valeur « V » ou « F » d’un groupe de chats, sans se soucier de leur état, déplacer les bols de nourriture de la pièce « V » vers la pièce « F » et inversement, par des chemins qui ne se croisent pas (s’ils se croisaient, le chat pourrait changer de bol au moment du croisement).

3. Afin de rattraper le coche si un chat décide malgré tout d’aller explorer la maison : pour dire « V » à une personne, mettre non seulement votre chat dans votre pièce « V » mais également ceux de vos voisins dans leur pièce « V ». En discutant avec vos voisins et votant à la majorité, la personne aura plus de chances d’obtenir le bon message, même si l’une des maisons du quartier a subi de fortes perturbations.

Adapter ces mécanismes de protection au support physique « bit quantique » est le grand défi pour la construction d’un ordinateur quantique. Afin de développer un peu d’intuition pour cet enjeu, nous allons d’abord parler du « bit aléatoire ».

Un premier pas vers le calculateur quantique : apprivoiser le hasard

Si certains chats rebelles répondent « miaou » ou non de manière aléatoire, on peut se servir de ce hasard pour accélérer des calculs (voir l’encart Monte-Carlo ci-après). Les mécanismes de stabilisation expliqués ci-dessus, permettent même de piloter précisément le résultat obtenu de ces rebelles. Les « nombres aléatoires » sont ainsi devenus un élément de base de nos ordinateurs depuis plusieurs décennies.

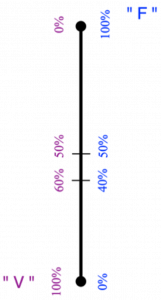
Figure 3 : Représentation d’un bit aléatoire, prenant la valeur « V » ou « F » avec une probabilité entre 0 et 1. La probabilité — utilisée pour générer chaque échantillon — se représente par une valeur le long du segment ; mais la lecture d’un échantillon fournira juste, au hasard, une des deux valeurs extrêmes « V » ou « F ».

L’idée du « bit aléatoire » est de disposer d’un électron dont la position « V » ou « F » est aléatoire, selon des probabilités bien définies : par exemple, pour chaque électron indépendamment, 60.00 % de chances de tomber dans « V » et 40.00 % de tomber dans « F ».
On peut visualiser cela en ajoutant, entre les deux valeurs du « bit » standard, un segment vertical (voir la figure 3 ci-contre) : le point en bas correspond comme sur la figure 1 à 100 % de chances d’être en « V », le haut à 100 % d’être en « F » donc 0 % d’être en « V », et le long du segment, on gradue les probabilités intermédiaires. Notez bien que le point milieu de ce segment ne représente pas du tout un électron qui se baladerait physiquement « entre » les positions stables « V » et « F » : il représente un électron qui a 50.00 % de chances d’être en « V » et 50.00 % d’être en « F », mais bien certain de rester à sa place. Par ailleurs, au moment de lire le résultat, on verra dans quelle case se trouve l’électron, mais rien ne permettra de vérifier s’il avait bien 50 % de chances de se trouver en « V », ou 51 % ou 60 % : pour cela, donc pour connaître la valeur sur le segment gradué, il faudrait accumuler des statistiques.

Le bit aléatoire est ainsi une ressource intermédiaire entre :

• un bit fixé — qui ne peut encoder que deux valeurs « V » ou « F » — et
• une valeur précise entre 0 et 1 (par exemple 60 %) — qui est utilisée pour générer le bit aléatoire, mais que l’on ne peut pas « lire » à partir d’un seul échantillon.

Tentons maintenant brièvement de comprendre comment assurer le fonctionnement fiable d’une machine qui utiliserait de vrais bits aléatoires — cela nous rapproche en effet du fonctionnement envisagé pour l’ordinateur quantique.

La première tâche pour cette machine serait donc de générer des valeurs au hasard, comme lorsqu’on joue à pile ou face. Le principe est un peu l’inverse des boîtes à œufs : la machine doit être conçue pour que n’importe quelle petite incertitude ait un effet tellement grand sur la position finale de l’électron, que cette position est en pratique imprévisible. Mais il ne s’agit pas de faire n’importe quoi : ce hasard doit être « piloté » pour s’assurer que les tirages satisfont, en très bonne approximation, à des probabilités bien définies : par exemple, 60.00 % de chances de tomber dans la zone « V » et 40.00 % de tomber dans la zone « F », ou plus souvent 50.00 % de tomber dans chaque zone. La technique de distillation, inspirée des codes correcteurs d’erreur (voir encart ci-dessous), permet de garantir des probabilités très précises à partir d’un processus peu calibré.

Une seconde tâche est d’assurer que le calcul reste protégé des perturbations éventuelles, quel que soit le résultat des tirages aléatoires. Heureusement, rallumer les boîtes à œufs remplit très bien ce rôle. En effet, elles empêchent les électrons de changer de zone, peu importe où ils étaient. Si le premier électron avait donc 60.00 % de chances de se retrouver dans la zone « V » à la fin de sa promenade aléatoire, il suffit de rallumer la boîte à œufs pour s’assurer qu’il aura toujours 60.00 % de s’y trouver en attendant la suite du calcul. On peut même faire tourner la boite afin d’effectuer des opérations, sans aucune erreur, avant de regarder où se trouvait l’électron.

En résumé, les mécanismes de protection mis en place pour l’ordinateur numérique s’adaptent bien pour calculer de manière fiable avec des « bits aléatoires ». Cette ressource est a priori plus riche qu’un « bit », mais ne répond toujours que par « V » (miaou) ou « F » (pas-miaou). Le « bit quantique » est une ressource encore plus riche, mais répondant toujours uniquement par « V » ou « F ». L’accélération spectaculaire que permettrait une machine quantique pour certains calculs n’avait rien d’évident, et la stabilisation de ce nouveau support physique tout en effectuant des opérations demeure un défi. Ainsi, il a fallu attendre Peter Shor en 1994 — plus d’un demi-siècle après avoir bien ancré la physique quantique — pour entrevoir concrètement le potentiel révolutionnaire du « calcul quantique ». Parlons donc un peu plus de cette machine quantique.

La nouvelle dimension du calculateur quantique

Un chat quantique peut se balader dans des dimensions « imaginaires » : au lieu d’être juste mort ou vif, il peut choisir une « phase quantique » pour devenir « mort + vif », puis « mort – vif », etc. Ainsi, à la fin d’un calcul, on pourra décider de mesurer si le chat est plutôt « mort » que « vif », ou de mesurer s’il est plutôt « mort + vif » que « mort – vif ». C’est la principale bizarrerie à admettre, et elle ouvre des possibilités spectaculaires !

En y regardant de très près, la physique quantique nous a appris que chaque fois que l’on peut se demander si un objet est en « V » ou en « F », il est en principe possible de se poser des questions alternatives, concernant des « combinaisons » de ces états. Les règles de ce « pile ou face quantique » peuvent se visualiser par une sphère (voir la figure 4 ci-dessous — nous verrons plus loin comment les relier à des supports physiques concrets). Comme pour le « bit aléatoire », la position dans la sphère représente les probabilités générant les résultats de lecture, elles ne seraient observables qu’en cumulant des statistiques. Ce qui change fondamentalement pour le « bit quantique » ou « qubit », c’est qu’à chaque tirage, l’on peut choisir un axe de lecture. Ainsi, en choisissant l’axe de lecture vertical, on obtient « V » ou « F » comme pour le « bit aléatoire », avec plus de chances d’obtenir « F » si le « bit quantique » est décrit par un point plus haut dans la sphère. En choisissant l’axe horizontal sur la figure, on obtient au hasard l’une des extrémités de cet axe, donc « 50 % V + 50 % F » ou « 50 % V – 50 % F », avec plus de chances d’obtenir « 50 % V – 50 % F » pour un « qubit » plus à gauche sur la figure. En sélectionnant un axe intermédiaire, on peut choisir de distinguer par exemple si l’on est plutôt en « 70 % V + 30 % F » ou en « 30 % V – 70 % F » ; ou encore, si l’on est plutôt en « 50 % V + i 50 % F » ou en « 50 % V – i 50 % F » (pour ceux qui connaissent les nombres complexes : une rotation autour de l’axe vertical correspond à changer l’argument complexe entre V et F).

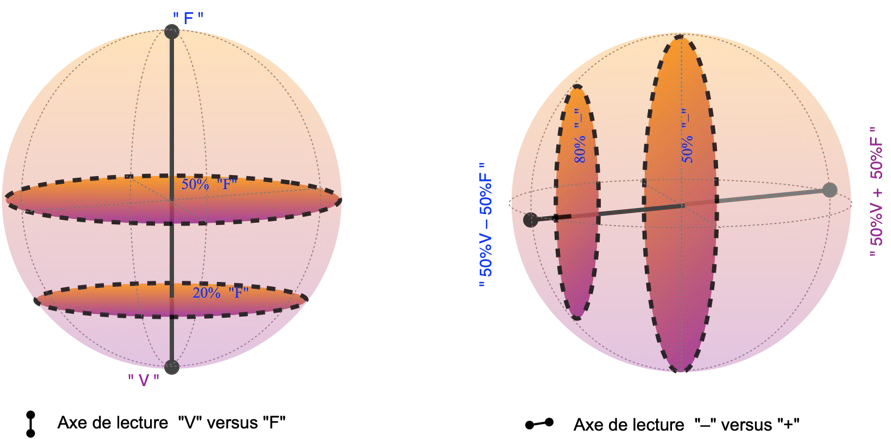
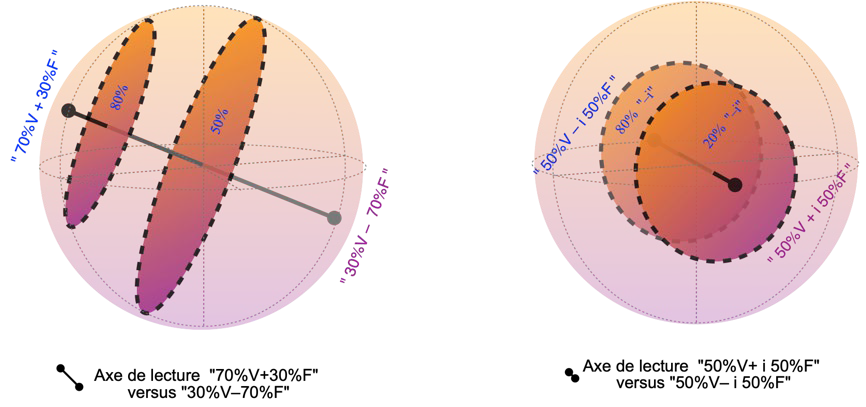
Représentation d’un bit quantique, qui fournit des valeurs aléatoires dans une base à choisir. Les probabilités utilisées pour générer chaque échantillon se représentent par une valeur dans la sphère, appelée sphère de Bloch. La lecture d’un échantillon correspond à choisir un axe passant par le centre de la sphère, afin d’obtenir, au hasard, une des deux valeurs extrêmes de cet axe. Ainsi, un qubit décrit par le point « F » par exemple donnera toujours le résultat « F » si nous le lisons selon l’axe vertical (figure un haut à gauche) ; mais il donnera aléatoirement « 50 % V – 50 % F » ou « 50 % V + 50 % F », avec des probabilités égales, si nous choisissons de le lire selon l’axe horizontal (figure en haut à droite). Tout axe de lecture est possible (cf d’autres exemples sur les figures du bas). Le calcul numérique quantique peut être formulé en utilisant uniquement les deux bases « V » versus « F » et « – » versus « + » (haut).

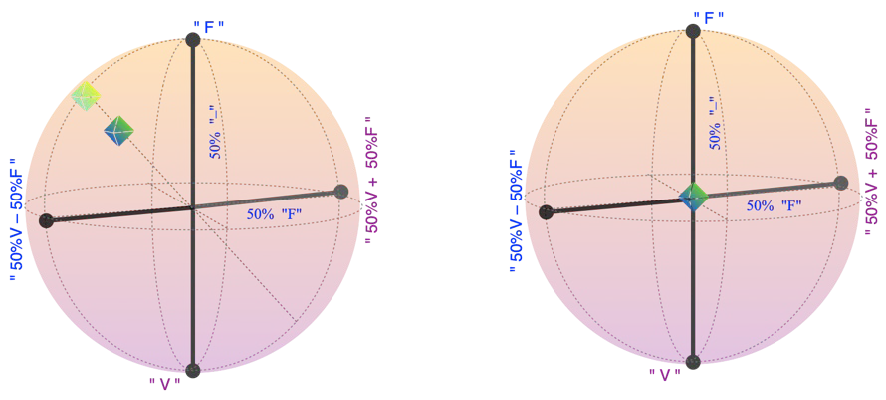
Exemples d’états d’un qubit (symbolisé par un cube) : à gauche, le cube clair, à la surface de la sphère, donnerait à 100 % « haut à gauche » si l’on mesurait selon l’axe pointillé sur lequel il se trouve. Selon l’axe vertical, il donnerait « F » avec environ 87% de chances. Selon l’axe horizontal, « – » avec environ 83 % de chances. Le cube foncé, dans la sphère, est plus incertain selon toutes les directions; en particulier, en mesurant selon son axe pointillé, on n’aura que 83 % de certitude environ. À droite, un qubit au centre de la sphère, donnera des résultats 50 % incertains, pour chaque axe de lecture : c’est finalement juste un bit aléatoire 50/50.

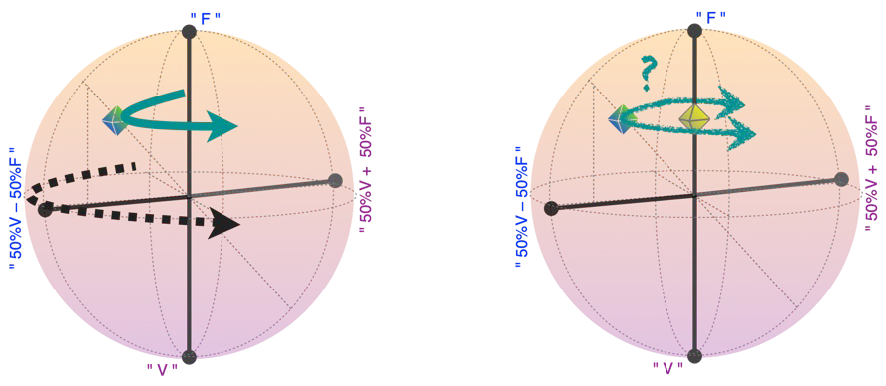
Physiquement, la phase du qubit tourne (figure de gauche, flèche pleine turquoise) à une vitesse proportionnelle à l’écart d’énergie entre « V » et « F ». Si l’on connait très bien cette vitesse, alors on peut la suivre avec nos instruments de mesure et de manipulation (flèche pointillée noire), et la situation effective est la même que si le qubit ne tournait pas. Par contre si l’énergie exacte et donc la vitesse de rotation est un peu aléatoire (figure de droite), alors après un certain temps, nous devenons très incertains sur ce que donnerait une mesure « – » versus « + ». On a donc effectivement un résultat aléatoire selon la direction « – » versus « + » (ainsi que les autres directions horizontales), et toutes les mesures répondent comme pour un qubit sur l’axe vertical (cube clair). Ce dernier n’est pas plus intéressant qu’un bit aléatoire standard (Figure 3).
NB : cette rotation est juste une manière de visualiser la phase quantique. Il n’y a aucun lien avec la rotation, bien réelle, de la boite à œufs en figure 2.

Figure 4 : illustration du « qubit » sur la sphère de Bloch.

D’après ces règles du jeu, un qubit dont l’état serait décrit par le point « 50% V – 50 % F » sur la surface de la sphère, indique bien que nous explorons aléatoirement les possibilités « V » ou « F » avec 50 % de chances chacune, comme avec un « bit aléatoire » ; mais en même temps, nous sommes 100 % certains du résultat que nous obtiendrions si nous mesurions le qubit selon l’axe horizontal. Le grand intérêt porté à l’ordinateur quantique provient du fait que les modifications que cela implique pour des machines de grande taille sont beaucoup plus spectaculaires par rapport au bit aléatoire, parfois même difficiles à concilier avec notre conception du monde (cf « inégalités de Bell » ou « théorème de Kochen-Specker »). C’est en explorant ces conséquences que l’on s’est aperçu que combiner des opérations sur des « bits quantiques » avant de les lire, permet d’accélérer significativement certains calculs (voir l’encart Deutsch-Josza plus loin).

Ainsi, selon la représentation de la figure 4, le bit quantique prend la dimension d’une sphère sur laquelle on peut distinguer, par rapport au bit aléatoire, des rotations autour de l’axe vertical. L’angle correspondant à cette rotation, par exemple 0° pour « 50 % V + 50 % F » et 180° pour « 50 % V – 50 % F », s’appelle d’ailleurs la « phase quantique ». Mais par quelle propriété physique est-elle pilotée ? En fait, la « phase quantique » tourne à une vitesse dE reflétant la différence d’énergie entre les états « V » et « F ». Lorsque l’on combine plusieurs qubits, en les faisant interagir durant le temps d’une opération on attribue des énergies différentes à « VV »,  « VF », « FV » et « FF », et l’on pilote ainsi les différentes phases associées ; et ainsi de suite pour des machines plus grandes. Le problème, c’est que cette rotation est extrêmement sensible. En effet, lorsque le moindre couplage imprévu du qubit à son environnement peut venir perturber la différence d’énergie entre « V » et « F », la vitesse de rotation devient incertaine, et la valeur de la « phase quantique » devient de plus en plus incertaine au cours du temps. Après un certain temps de rotation à des vitesses inconnues, nous ne pourrons plus prédire du tout le résultat d’une mesure selon un axe horizontal : a priori, il sera totalement aléatoire, ce qui s’exprime par un état sur l’axe vertical dans la sphère de Bloch (voir le bas de la figure 4). Le qubit se réduirait ainsi à un bit aléatoire contrôlé selon l’axe vertical (comme pour la figure 3), avec pour seule prime un résultat aléatoire 50/50 si l’on décide plutôt de mesurer selon un axe horizontal. Afin de bénéficier des « avantages quantiques », il faut donc mettre en place des mécanismes de protection.

Sauvons le chat quantique de son extinction !

Vous ne verrez pas de chat « vivant + mort » tous les jours, car ces créatures sont extrêmement sensibles. En effet, si l’énergie d’un chat vivant était connue avec une incertitude d’un seul photon de lumière visible, alors la phase «vivant ± mort» serait brouillée… un million de milliards de fois par seconde (10¹⁴ – 10¹⁵ Hz, fréquence de la lumière). On comprend dès lors à quel point il est difficile de percevoir la phase quantique à l’échelle humaine, et de la contrôler pour l’opération d’une « machine quantique ».

Les trois niveaux de protection numérique s’appliquent aussi à l’ordinateur quantique, mais avec des complications importantes.

Premièrement, nous chercherons à nouveau à contrôler quelques valeurs bien distinctes, qui suffiront à effectuer tous les calculs possibles (« machine universelle ») en combinant plein de qubits. D’abord, comme pour un bit classique, la valeur de bit « V » ou « F » peut être vue comme deux positions bien distinctes d’un électron. Il vient s’y ajouter la valeur de phase quantique « + » ou « – », qui correspondrait plutôt à des différences d’énergie spécifiques entre ces deux positions. Malheureusement, peu importe les valeurs d’énergie choisies, la même petite énergie accidentelle dE suffira à troubler la phase, extrêmement sensible,  jusqu’à brouiller totalement sa valeur numérique « + » ou « – » après un temps très court. De plus, si éloigner les deux positions « V » et « F » permet de diminuer le risque qu’une perturbation fasse sauter cette valeur, il devient plus difficile à grande distance de garantir une différence d’énergie donnée entre zones « V » et « F » afin de maintenir la phase « + » ou « – ». Cela rend très difficile le pilotage d’un qubit. Au prix d’un immense effort technologique, les machines quantiques actuelles ont démontré la capacité à effectuer de petits calculs avant que des perturbations et imprécisions ne brouillent trop ces valeurs. Mais pour faire des calculs plus longs et vraiment utiles, il faudra ajouter des éléments de protection. Une première piste de recherche consiste à chercher des encodages numériques plus rusés : en fonction des perturbations attendues, distribuer les zones « V » et « F » de manière à limiter les imprécisions à la fois en « bit » et en « phase ». D’autres pistes considèrent une protection plus active, en adaptant des mécanismes comme ceux décrits plus haut : « boîte à œufs » et/ou codes correcteurs d’erreurs. La mise en place de ces mécanismes de protection est le principal défi actuel pour la construction d’un ordinateur quantique.

Le second niveau de protection concerne donc un mécanisme de rappel vers les valeurs cibles, type « boîtes à œufs » (voir la figure 2). Des travaux récents [Biblio 1] ont démontré la possibilité de protéger ainsi la valeur de bit, empêchant très efficacement un saut entre « V » et « F » comme pour le bit standard, sans trop augmenter le risque d’un saut entre « + » et « – » du bit quantique. Par contre, un mécanisme de rappel de la phase paraît bien plus compliqué à concevoir. En effet, la caractéristique physique concernée (intégrale de l’énergie) n’est pas directement détectable. Cependant, des encodages plus rusés (cf premier niveau de protection) pourraient rendre très improbables les processus physiques susceptibles de donner des énergies différentes à « V » et « F ». Les recherches en ce sens sont très actives depuis quelques années, entre développements théoriques et implémentations expérimentales.

Le troisième niveau de protection numérique se construit sur la redondance des codes correcteurs d’erreur — pour rappel, dire « VVVVV » pour « V ». Celui-ci également se généralise à la protection de bit et phase quantique, mais au prix de codes beaucoup plus longs et plus difficilement compatibles avec des opérations de calcul. C’est l’une des raisons principales pour lesquelles tellement d’efforts sont nécessaires sur les autres modes de protection.

Enfin, une dernière difficulté concerne les opérations de calcul. De fait, utiliser la nouvelle dimension « phase quantique » dans des calculs implique de nouvelles opérations à effectuer entre les qubits. Certaines d’entre elles nécessitent des complications importantes par rapport à « tourner la boîte à œufs ». Une piste serait de façonner ces opérations par distillation, généralisant au cas quantique les principes de l’encart « Comment générer un hasard précis ».

Alors, à quand le chat quantique domestiqué ?

Pour effectuer un calcul sur base de chats quantiques, il faudrait contrôler la position et l’énergie de toute une meute, en les faisant interagir par petits groupes, panacher ces groupes au cours du temps, … autant dire que ce n’est pas encore pour tout de suite.

Vous l’aurez compris, il n’est pas évident de concevoir des supports physiques suffisamment stables pour encoder de l’information quantique. Même la position d’un seul électron, dont nous nous sommes servis comme exemple visuel, serait trop sensible à des sollicitations extérieures. En pratique, on essaie de contrôler des variables physiques plus abstraites, comme les modes d’oscillations d’ions ou des états du champ électromagnétique (micro-ondes, lumière), etc. ; les « boîtes à œufs » sont à concevoir à ce niveau abstrait, en tant que forces d’interaction et d’amortissement. Le principe reste le même : on doit ruser pour protéger au maximum l’information quantique de toutes les perturbations qui pourraient l’atteindre, tout en nous permettant d’effectuer des opérations rapides, sur des machines de plus en plus grandes.

L’état de l’art, début 2021, se concentre sur deux approches. La première consiste à développer des briques de base — un seul qubit — de plus en plus précises. Le but est d’atteindre des erreurs inférieures à 0.001 %  (un ordinateur classique actuel en commet moins de 10^-15), sur des architectures prometteuses pour développer un processeur conséquent. En effet, un qubit isolé aux confins de l’univers serait très stable, mais sans l’intégrer dans une machine, on ne pourra jamais s’en servir afin de calculer. Pour l’instant, des plateformes basées sur des ions piégés ou sur des circuits supraconducteurs à des températures proches du zéro absolu, atteignent souvent de l’ordre de 0.1 % à 1 % d’erreur sur leurs composants [Biblio 2]. En gagnant un facteur 100 sur cette précision, tout en agrandissant la taille des machines, les méthodes de codes correcteurs d’erreurs deviendraient efficaces. En parallèle des améliorations de matériel, on cherche à maîtriser des encodages d’information plus compliqués mais plus stables, comme les « états GKP » ou les « qubits Majorana ». La seconde approche consiste à construire des réseaux de taille modérée, en se satisfaisant de qubits plus ou moins précis — typiquement de l’ordre de 1 % d’erreur — et d’essayer de se servir des « effets quantiques »  résiduels, même s’ils ne sont pas parfaits. Ce genre d’approche, baptisée « NISQ » (pour noisy intermediate-scale quantum), ne semble pas encore pouvoir accélérer des calculs utiles, mais démontre au moins des principes utiles pour contrôler plusieurs centaines de « qubits » [Biblio 2]. Elle inspire aussi de nouvelles approches de calcul sur les ordinateurs classiques actuels [Biblio 3]. De là à disposer d’un ordinateur quantique complet, contrôlant des milliers ou millions de qubits avec précision afin de résoudre des problèmes utiles à la société, il reste du pain sur la planche — et pas mal de pistes qui progressent rapidement. Plus que jamais, le rêve est bien vivant (± mort) !