De la deuxième à la troisième dimension
Disposer d’une représentation en trois dimensions de notre environnement, c’est-à-dire connaître la position, les dimensions et l’orientation des objets et des volumes qui nous entourent, est souvent très utile.
C’est en particulier le cas lorsque l’on souhaite visualiser l’impact d’un nouveau bâtiment dans un environnement urbain, apprendre à un robot à se déplacer de façon autonome dans un lieu industriel ou encore réaliser certains effets spéciaux au cinéma.
Cette reconstitution d’un espace réel en trois dimensions est une tâche à la fois laborieuse et coûteuse.
C’est pourquoi la recherche en vision par ordinateur se consacre à ces problématiques : il s’agit de trouver une solution simple qui permette de construire, si possible en temps réel, le modèle 3D d’un environnement.
Il est, par exemple, assez facile de recueillir des informations sur un lieu ou un objet en le prenant en photos sous divers angles. Dès lors, ne serait-il pas possible, à partir de ces clichés, de reconstruire en trois dimensions un espace ou un volume fidèle à la réalité ?
Petite approche théorique
Géométriquement, en quoi consiste une prise de vues photographique ?
Prendre une photo c’est projeter chaque point visible de l’environnement 3D sur un point 2D du plan de la pellicule photo. Le rayon optique est la ligne qui relie entre eux ces deux points, en passant par le centre optique de l’appareil.
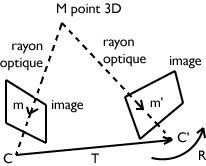
Principe de la stéréoscopie.
On considère deux caméras dont les centres optiques sont notés C et C’, dont la position relative est spécifiée par une translation T et l’orientation relative par une rotation R.
Pour chaque point de l’espace M, le fait que le rayon optique passant par m issu de C et le rayon optique passant par m’ issu de C’ se coupent en M induit une contrainte géométrique, dite « épipolaire ».
Imaginons maintenant que l’on prenne un deuxième cliché de la même scène, mais cette fois depuis un autre angle de vue ; chaque point visible de l’espace 3D sera alors le point de départ d’un nouvel axe optique, qui passera lui aussi par la cellule de l’appareil photo pour finir sa course sur la pellicule.
Appelons M un point quelconque de notre environnement en 3D : m et m’ sont les images de M sur chacun des deux clichés. La position géométrique du point M se trouve alors à l’intersection des rayons optiques le reliant respectivement à m et à m’. Théoriquement, il est alors possible de reconstituer, à partir des seules photographies en 2D, la réalité 3D dont elles sont l’image, de faire « revivre » M dans un espace réel.
Comment ça marche ? L’ensemble formé par les trois points (M, m et m’) et par les droites qui les relient définit ce que l’on appelle la contrainte épipolaire. C’est la tâche de la géométrie épipolaire que d’aider à reconstruire la « troisième dimension » de M.
Quels paramètres pour calibrer la géométrie ?
En pratique, bien sûr, les choses sont un peu plus compliquées. Lorsque l’on prend deux images d’un environnement réel, on ne connaît généralement pas de façon très précise les positions successives de l’appareil photo, ni ses paramètres optiques, ni enfin l’angle de chaque prise de vue. Pourtant, la géométrie épipolaire est entièrement dépendante de toutes ces données, qui constituent la base de ses calculs. C’est pourquoi il est nécessaire de « calibrer », c’est-à-dire d’estimer ces paramètres.
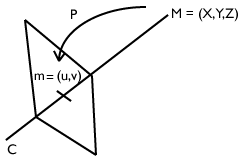
Le point correspondant d’un point M de l’environnement réel de coordonnées M = (X,Y,Z) dans le plan image de la photo est un point 2D de coordonnées m = (u,v). Il est le transformé de ce point M par la matrice de projection perspective de l’appareil photo et u et v sont fonction de X, Y et Z selon deux équations comprenant au total 11 paramètres.
Les deux relations sont de la forme suivante :
u = (P1 X + P2 Y + P3 Z + P4) / (P9 X + P10 Y + P11 Z + 1)
v = (P5 X + P6 Y + P7 Z + P8) / (P9 X + P10 Y + P11 Z + 1)
Les onze coefficients, P1 à P11, expriment les relations entre les points de l’environnement 3D et les points correspondants du plan image d’une photo. Ils se définissent à partir des paramètres optiques des caméras (les distances focales, la position du centre optique) et des paramètres extrinsèques de position et d’orientation des caméras dans l’espace.
Avec deux images, ces relations sont à prendre en compte pour chaque image, car les coordonnées m’ = (u’,v’) sont aussi fonction de X, Y et Z, introduisant deux nouvelles relations.
Si l’on connaît ces coefficients, on peut calculer X, Y et Z à partir de trois de ces quatre relations, donc reconstruire le point M, et il reste une relation supplémentaire qui lie les coordonnées de m et m’. Cette relation correspond à la contrainte épipolaire.
Si on ne connaît pas encore ces coefficients, c’est en posant que la contrainte épipolaire doit être vérifiée pour des points m et m’ connus que l’on obtient des équations qui permettent de les estimer. Ces équations ont-elles une solution ? Une solution unique ? Tout le travail théorique a été d’expliquer sous quelles conditions on trouvait une telle solution.
Très souvent la solution est trouvée à un facteur d’échelle (ou à plusieurs facteurs) près. Dans ce cas, on reconstruit les points 3D en fixant ces facteurs d’échelle à partir de connaissances a priori ou en laissant l’utilisateur les ajuster. En pratique, ces facteurs sont faciles à fixer, par exemple si on connait la taille d’un objet.
Le passage de la théorie à la pratique impose aussi de prendre en compte les distorsions optiques de la lentille, qui peuvent affecter les mesures, même si ces effets sont souvent négligeables.
Au total, ce ne sont pas moins de onze coefficients qu’il faut déterminer pour parvenir à connaître les relations entre un point de l’univers réel et son image sur un cliché.
Mais, on l’a vu, deux photos au moins sont nécessaires pour procéder à une reconstruction 3D. Dès lors, il faut calibrer les paramètres liés à chacune des projections, puis enfin les combiner entre eux.
Comment calibrer la géométrie épipolaire ?
Pour réaliser cette calibration, on définit un certain nombre de points de repère. L’objectif est de mettre en relation des couples de points issus des deux photos (par exemple m et m’) et représentant dans la réalité le même point M. Les relations établies entre ces points de repère fournissent une ou plusieurs équations. Pour simplifier la tâche, on utilise des stratégies dites d’optimisation, afin de déterminer les paramètres les plus efficaces et les plus simples à manier.
Comment demander à un ordinateur de résoudre des équations compliquées ? Alors qu’il y a parfois plusieurs solutions… ou pas de solution exacte !… et que — comme c’est souvent le cas en pratique — les mathématiques ne peuvent nous renseigner…
Il existe une méthode, dite d’optimisation, qui fournit automatiquement une solution raisonnable. La clé de voûte de cette méthode est de partir d’une valeur « par défaut » proposée par l’utilisateur, puis de laisser l’ordinateur améliorer cette valeur. On obtient alors une solution « locale » (c’est-à-dire, parmi toutes les solutions possibles, proche de la valeur par défaut) et approchée (qui ne vérifie pas les équations mais « presque »).
Pour cela, on considère toutes les équations du problème : 0 = eq1(x), 0 = eq2(x)… Ici x = (x1, x2, …) rassemble toutes les inconnues dont on cherche une solution et eq1( ), eq2( )… sont les expressions mathématiques qui définissent les équations. On va combiner ces expressions en un seul critère, choisi pour que :
- il égale 0 si toutes les équations sont égales à zéro ;
- il soit d’autant plus grand que une ou plusieurs expressions définissant les équations ne sont pas égales à zéro.
Par exemple, prenons le critère c = | eq1(x) | + | eq2(x) | + … où on ajoute toutes les expressions entre elles, en valeur absolue (donc en enlevant le signe + ou -). Ce critère est intéressant car pour que cette somme de nombres positifs soit nulle, tous les nombres doivent être nuls, et surtout, ce nombre diminue au fur et à mesure que les valeurs des expressions diminuent.
La méthode est alors très simple : calculons c pour la valeur par défaut, puis modifions un peu cette valeur par défaut dans un sens et recalculons c . Si c a diminué, alors nous avons « amélioré » la valeur par défaut et nous recommençons ; sinon nous faisons varier la valeur par défaut dans un autre sens et recalculons c pour voir si cela s’est amélioré. Nous recommençons tant que nous pouvons améliorer le résultat dans un sens ou dans un autre, nous arrêtons sinon.
Dans le cas où il y a plusieurs solutions, on choisit donc une solution proche de la valeur par défaut proposée, la plus proche au sens de la recherche effectuée précédemment. On peut aussi ajouter des contraintes : par exemple, rechercher la solution la moins coûteuse et minimiser ce coût avec la présente méthode.
Dans le cas où il n’y a pas de solution exacte, on choisit une solution approchée, la « meilleure » au sens du critère précédent. On obtient d’ailleurs aussi un indice de « qualité » la solution étant d’autant meilleure que le critère est peu élevé. On peut alors comparer plusieurs solutions.
Ce principe très général est la base des méthodes les plus efficaces d’estimations de paramètres, comme dans le cas de la calibration décrit ici. Il s’applique dans de multiples situations :
- amélioration par l’ordinateur d’une solution approchée proposée par un utilisateur, qui peut apprécier le résultat, faire une nouvelle proposition, etc.
- adaptation d’une solution précédente dans le cas d’un changement, par exemple lors du suivi d’un objet mobile dont on estime les paramètres, etc.
- recherche automatique de solution, par exemple en faisant des tirages aléatoires ou en partant de solutions préenregistrées, en les améliorant et en gardant la meilleure solution trouvée.
Ce qui est très intéressant, c’est que n’importe quel élément de la scène visuelle peut être utilisé comme point de repère, à condition qu’il soit fixe et bien identifiable sur chacun des clichés.
Pour obtenir les points de repère, il faut définir les coordonnées des points correspondants dans les deux images. Les ordinateurs viennent ici nous simplifier la tâche : la sélection des points de repères dans les photos peut se faire en un seul clic et des méthodes de traitement d’image permettent de raffiner la correspondance entre ces points ou même de les déterminer automatiquement.
Pour accéder à l’applet Java, autorisez les applets du domaine https://interstices.info. Si votre navigateur n’accepte plus le plug-in Java, mais que Java est installé sur votre ordinateur, vous pouvez télécharger le fichier JNLP, enregistrez-le avant de l’ouvrir avec Java Web Start.
Cliquez sur un point dans une vue, vous verrez – grâce aux paramètres de calibration qui ont été estimés au préalable – la projection des rayons optiques s’afficher dans les autres images : ce sont les lignes épipolaires.
Cliquez alors sur le même point dans une des autres images : le voilà localisé à l’intersection de deux lignes, donc localisé dans toutes les vues.
En bas à droite, un petit afficheur 3D juste pour jouer : si vous faites tourner les points avec la souris, vous les verrez bouger en 3D.
Si vous avez de la patience, définissez une bonne dizaine de points pour regarder cet effet.

Deux images peuvent suffire à créer un modèle 3D.
En haut : deux photos du même lieu ;
En bas : deux images du modèle 3D reconstruit à partir de ces photos.
Les points cachés dans une vue et présents sur l’autre ne peuvent être mis en correspondance, ils sont alors détectés et mis de côté.
Malgré tout, il reste une marge d’erreur dans la localisation des points de repère, liée principalement au manque de précision des clichés photographiques. Pour compenser cet inconvénient et réduire ses effets, on utilise donc une multitude de points de repères.
Dans certains cas, le nombre de paramètres peut être facilement réduit, par exemple lorsque la focale de l’appareil photo ou de la caméra est connue, ou lorsque l’on connaît précisément les coordonnées de certains points M de l’environnement 3D.
Dans d’autres cas en revanche la calibration ne peut être calculée qu’à certains facteurs près. Ces paramètres résiduels restent à ajuster par l’utilisateur.
Une fois ces paramètres calibrés, deux points en correspondance dans deux images différentes suffisent effectivement pour déterminer la position 3D d’un point de l’environnement réel. Bien sûr, plus on multiplie les images et les correspondances, et plus le résultat sera précis.
Application en cinématographie

Un hélicoptère « reconstitué » à l’aide d’ImageModeler.
Effets visuels © Artifex Studios Ltd
L’intégration d’objets virtuels dans un décor réel est à la base de nombreux effets cinématographiques : ce sont les fameux effets spéciaux.
Il peut s’agir de reconstituer un objet à partir de photographies, par exemple un hélicoptère qui sera ensuite incrusté dans une séquence de vues aériennes. Il peut aussi s’agir d’intégrer à une scène réelle des éléments créés en images de synthèse, par exemple des dinosaures.
Pour commencer, il est nécessaire de reconstruire dans l’ordinateur les composantes soit de l’objet, soit du décor réel, c’est-à-dire d’en faire des formes géométriques virtuelles qui pourront être facilement manipulées. C’est ce que propose par exemple la société Realviz avec ImageModeler, un logiciel de modélisation par l’image qui s’appuie sur la géométrie épipolaire.

Étapes de l’utilisation d’ImageModeler
(image mise gracieusement à disposition par Realviz). © Realviz
Pour débuter un projet dans ImageModeler, l’utilisateur doit prendre plusieurs photographies (au moins deux) de l’objet à partir de différents points de vue. Il n’y a pas besoin d’appareil photo spécial : un appareil photo numérique classique suffit.
Une fois les photos importées dans le logiciel, l’utilisateur doit trouver et indiquer des points en commun sur les photos (de 9 à 20 points). ImageModeler calibrera automatiquement les caméras (position, rotation, focale, distorsion).
Il s’agit ensuite de créer le modèle, en mesurant les distances et les angles de la scène, en créant des faces à partir de points, etc. et d’extraire les textures.
Plus d’informations sur le site de présentation d’ImageModeler.
La manipulation est bien sûr particulièrement délicate dans le cas de plans en mouvement. Pour une vue panoramique, la caméra tourne sur place sans se déplacer, et le modèle doit lui aussi tourner. Si la caméra tourne autour d’une scène figée, la situation est plus complexe encore, car la translation induite génère de la parallaxe, des objets apparaissent ou disparaissent, etc.
Application en robotique
Si la localisation manuelle des points de repère se conçoit bien lorsqu’il s’agit de reconstituer un environnement architectural ou un décor de cinéma, elle devient par contre plus difficile en vision robotique.

Trois caméras montées sur un robot mobile.
Ce système de vision rudimentaire lui permet de détecter les bords d’un couloir ou d’une chaussée.
En effet, le robot doit être capable de se repérer en permanence dans son environnement, ce qui constitue un défi d’une tout autre ampleur !
La localisation manuelle est alors remplacée par la reconnaissance de blocs de pixels dans les images. La recherche de mise en correspondance de blocs de pixels dans les images de deux caméras ou dans deux images successives d’une même caméra permet aux caméras de s’autocalibrer. Sur cette base, sont déterminées la position du robot et la position des obstacles de l’environnement 3D réel. Dans ce cas, on ne cherche pas à reconstruire précisément l’environnement mais à obtenir des informations minimales permettant au robot de se situer dans l’espace, d’éviter les obstacles, d’identifier l’objet qu’il recherche, etc.
Ce sujet est traité plus en détail dans un autre document, intitulé La grenouille et le robot.
Le passage de la 2D à la 3D, on le voit, n’est pas simple et nécessite de nombreux calculs. S’il ne résout pas tout, il reste une première étape incontournable… pour le dinosaure comme pour le robot !
Pour en savoir plus sur la vision par ordinateur, nous vous proposons quelques références.
Nous vous proposons de consulter :
- un cours de vision par ordinateur, par Frédéric Devernay, destiné aux étudiants ;
- le best-seller anglophone sur le sujet : Computer Vision: A Modern Approach de David A. Forsyth et Jean Ponce (Prentice Hall 2002) ;
- un article de vulgarisation scientifique : Perception visuelle en robotique : profiter de la biologie pour faire des systèmes adaptatifs, par Thierry Viéville et Olivier Faugeras, téléchargeable en pdf.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

